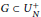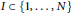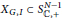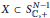Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mang, Alexander
and
Weber, Moritz
2021.
Categories of two-colored pair partitions Part II: Categories indexed by semigroups.
Journal of Combinatorial Theory, Series A,
Vol. 180,
Issue. ,
p.
105409.