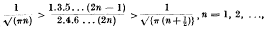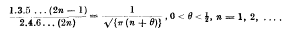Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mitrinović, Dragoslav S.
1970.
Analytic Inequalities.
p.
186.
Lorch, Lee
1984.
Inequalities for ultraspherical polynomials and the gamma function.
Journal of Approximation Theory,
Vol. 40,
Issue. 2,
p.
115.
Dutka, Jacques
1985.
On Some Gamma Function Inequalities.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 1,
p.
180.
Bustoz, Joaquin
and
Ismail, Mourad E. H.
1986.
On gamma function inequalities.
Mathematics of Computation,
Vol. 47,
Issue. 176,
p.
659.
Merkle, M.
2005.
Gurland's ratio for the gamma function.
Computers & Mathematics with Applications,
Vol. 49,
Issue. 2-3,
p.
389.
LI, LUOQING
2009.
REGULARIZED LEAST SQUARE REGRESSION WITH SPHERICAL POLYNOMIAL KERNELS.
International Journal of Wavelets, Multiresolution and Information Processing,
Vol. 07,
Issue. 06,
p.
781.
Grinshpan, Arcadii Z.
2010.
Weighted inequalities and negative binomials.
Advances in Applied Mathematics,
Vol. 45,
Issue. 4,
p.
564.
Mortici, Cristinel
2012.
Completely monotone functions and the Wallis ratio.
Applied Mathematics Letters,
Vol. 25,
Issue. 4,
p.
717.
Zhao, Jiao-Lian
Guo, Bai-Ni
and
Qi, Feng
2012.
Complete monotonicity of two functions involving the tri-and tetra-gamma functions.
Periodica Mathematica Hungarica,
Vol. 65,
Issue. 1,
p.
147.
2012.
Zeta and q-Zeta Functions and Associated Series and Integrals.
p.
603.
Qi, Feng
and
Luo, Qiu-Ming
2013.
Bounds for the ratio of two gamma functions: from Wendel’s asymptotic relation to Elezović-Giordano-Pečarić’s theorem.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Guo, Bai-Ni
Qi, Feng
Zhao, Jiao-Lian
and
Luo, Qiu-Ming
2015.
Sharp Inequalities for Polygamma Functions.
Mathematica Slovaca,
Vol. 65,
Issue. 1,
p.
103.
Qi, Feng
and
Guo, Bai-Ni
2016.
Complete monotonicity of divided differences of the di- and tri-gamma functions with applications.
Georgian Mathematical Journal,
Vol. 23,
Issue. 2,
p.
279.
Mortici, Cristinel
and
Cristea, Valentin Gabriel
2016.
Estimates for Wallis’ ratio and related functions.
Indian Journal of Pure and Applied Mathematics,
Vol. 47,
Issue. 3,
p.
437.
Qi, Feng
and
Guo, Bai-Ni
2017.
Integral Representations of the Catalan Numbers and Their Applications.
Mathematics,
Vol. 5,
Issue. 3,
p.
40.
Yang, Zhen-Hang
and
Zheng, Shen-Zhou
2017.
The monotonicity and convexity for the ratios of modified Bessel functions of the second kind and applications.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 7,
p.
2943.
Chashchina, O.I.
and
Silagadze, Z.K.
2017.
On the quantum mechanical derivation of the Wallis formula for π.
Physics Letters A,
Vol. 381,
Issue. 32,
p.
2593.
Lampret, Vito
2019.
A Simple Asymptotic Estimate of Wallis’ Ratio Using Stirling’s Factorial Formula.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 42,
Issue. 6,
p.
3213.
Yang, Zhenhang
and
Tian, Jing-Feng
2019.
Asymptotic expansions for the gamma function in terms of hyperbolic functions.
Journal of Mathematical Analysis and Applications,
Vol. 478,
Issue. 1,
p.
133.
Qi, Feng
and
Agarwal, Ravi P.
2019.
On complete monotonicity for several classes of functions related to ratios of gamma functions.
Journal of Inequalities and Applications,
Vol. 2019,
Issue. 1,