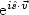We perform a complete study of the truncation error of the Jacobi-Anger series. This series expands every plane wave ${\rm e}^{i \hat{s} \cdot \vec{v}}$ in terms of spherical harmonics $\{ Y_{\ell, m}(\hat{s}) \}_{|m|\le \ell\le \infty} $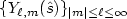. We consider the truncated series where the summation is performed over the $(\ell,m)$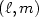's satisfying $|m| \le \ell \le L$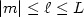. 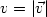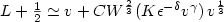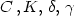We prove that if $v = |\vec{v}|$ is large enough, the truncated series gives rise to an error lower than ϵ as soon as L satisfies $L+\frac{1}{2} \simeq v + C W^{\frac{2}{3}}(K \epsilon^{-\delta} v^\gamma )\, v^{\frac{1}{3}}$ where W is the Lambert function and $C\,, K, \, \delta, \, \gamma$ are pure positive constants. Numerical experiments show that this asymptotic is optimal. Those results are useful to provide sharp estimates for the error in the fast multipole method for scattering computation.