We perform a complete study of the truncation error of the Gegenbauer series. This series yields an expansion of the Green kernel of the Helmholtz equation, $\frac{ {\rm e}^{i |\vec{u}-\vec{v}|}}{4 \pi i |\vec{u}-\vec{v}|}$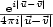, which is the core of the Fast Multipole Method for the integral equations. We consider the truncated series where the summation is performed over the indices $\ell \le L$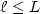. We prove that if $v = |\vec{v}|$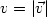 is large enough, the truncated series gives rise to an error lower than ϵ as soon as L satisfies $L+\frac{1}{2} \simeq v + C W^{\frac{2}{3}}(K(\alpha) \epsilon^{-\delta} v^\gamma )\, v^{\frac{1}{3}}$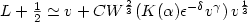 where W is the Lambert function, $K(\alpha)$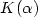 depends only on $\alpha=\frac{|\vec{u}|}{|\vec{v}|}$ 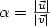and $C\,, \delta, \, \gamma$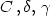 are pure positive constants. Numerical experiments show that this asymptotic is optimal. Those results are useful to provide sharp estimates of the error in the fast multipole method for scattering computation.