Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-04-30T22:19:06.362Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonparametric estimation of the derivatives of the stationary density for stationary processes

Published online by Cambridge University Press:  06 December 2012

Emeline Schmisser
Emeline Schmisser*
Affiliation:
UniversitéLille 1, Laboratoire Paul Painlevé, Cité Scientifique, 59655 Villeneuve d’Ascq, France.. emeline.schmisser@math.univ-lille1.fr
Get access

Abstract

In this article, our aim is to estimate the successive derivatives of the stationary density f of a strictly stationary and β-mixing process (Xt)t≥0. This process is observed at discrete times t = 0,Δ,...,nΔ. The sampling interval Δ can be fixed or small. We use a penalized least-square approach to compute adaptive estimators. If the derivative f(j) belongs to the Besov space \hbox{$\rond{B}_{2,\infty}^{\alpha}$}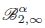B2,∞α, then our estimator converges at rate (nΔ)−α/(2α+2j+1). Then we consider a diffusion with known diffusion coefficient. We use the particular form of the stationary density to compute an adaptive estimator of its first derivative f′. When the sampling interval Δ tends to 0, and when the diffusion coefficient is known, the convergence rate of our estimator is (nΔ)−α/(2α+1). When the diffusion coefficient is known, we also construct a quotient estimator of the drift for low-frequency data.

Keywords

Derivatives of the stationary densitydiffusion processesmixing processesnonparametric estimationstationary processes.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 17 , 2013 , pp. 33 - 69
Copyright
© EDP Sciences, SMAI, 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

Arlot, S. and Massart, P., Data-driven calibration of penalties for least-squares regression. J. Mach. Learn. Res. 10 (2009) 245–279. Google Scholar
Barron, A., Birgé, L. and Massart, P., Risk bounds for model selection via penalization. Probab. Theory Relat. Fields 113 (1999) 301–413. Google Scholar
Beskos, A., Papaspiliopoulos, O. and Roberts, G.O., Retrospective exact simulation of diffusion sample paths with applications. Bernoulli 12 (2006) 1077–1098. Google Scholar
Bosq, D., Parametric rates of nonparametric estimators and predictors for continuous time processes. Ann. Stat. 25 (1997) 982–1000. Google Scholar
Comte, F. and Merlevède, F., Adaptive estimation of the stationary density of discrete and continuous time mixing processes. ESAIM : PS 6 (2002) 211–238 (electronic). New directions in time series analysis. Luminy (2001). Google Scholar
Comte, F. and Merlevède, F., Super optimal rates for nonparametric density estimation via projection estimators. Stoc. Proc. Appl. 115 (2005) 797–826. Google Scholar
Comte, F., Rozenholc, Y. and Taupin, M.L., Penalized contrast estimator for adaptive density deconvolution. Can. J. Stat. 34 (2006) 431–452. Google Scholar
Comte, F., Genon-Catalot, V. and Rozenholc, Y., Penalized nonparametric mean square estimation of the coefficients of diffusion processes. Bernoulli 13 (2007) 514–543. Google Scholar
Dalalyan, A.S. and Kutoyants, Y.A., Asymptotically efficient estimation of the derivative of the invariant density. Stat. Inference Stoch. Process. 6 (2003) 89–107. Google Scholar
DeVore, R.A. and Lorentz, G.G., Constructive approximation. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 303 (1993). Google Scholar
Gloter, A., Discrete sampling of an integrated diffusion process and parameter estimation of the diffusion coefficient. ESAIM : PS 4 (2000) 205–227. Google Scholar
Gobet, E., Hoffmann, M. and Reiß, M., Nonparametric estimation of scalar diffusions based on low frequency data. Ann. Stat. 32 (2004) 2223–2253. Google Scholar
Hosseinioun, N., Doosti, H. and Niroumand, H.A., Wavelet-based estimators of the integrated squared density derivatives for mixing sequences. Pakistan J. Stat. 25 (2009) 341–350. Google Scholar
C. Lacour, Estimation non paramétrique adaptative pour les chaînes de Markov et les chaînes de Markov cachées. Ph.D. thesis, Université Paris Descartes (2007).
Lacour, C., Nonparametric estimation of the stationary density and the transition density of a Markov chain. Stoc. Proc. Appl. 118 (2008) 232–260. Google Scholar
Leblanc, F., Density estimation for a class of continuous time processes. Math. Methods Stat. 6 (1997) 171–199. Google Scholar
Lerasle, M., Adaptive density estimation of stationary β-mixing and τ-mixing processes. Math. Methods Stat. 18 (2009) 59–83. Google Scholar
M. Lerasle, Optimal model selection for stationary data under various mixing conditions (2010).
Masry, E., Probability density estimation from dependent observations using wavelets orthonormal bases. Stat. Probab. Lett. 21 (1994) 181–194. Available on : http://dx.doi.org/10.1016/0167-7152(94)90114-7. Google Scholar
Y. Meyer, Ondelettes et opérateurs I. Actualités Mathématiques [Current Mathematical Topics]. Hermann, Paris, Ondelettes [Wavelets] (1990).
Pardoux, E. and Veretennikov, A.Y., On the Poisson equation and diffusion approximation I. Ann. Probab. 29 (2001) 1061–1085. Google Scholar
Rao, B.L.S.P., Nonparametric estimation of the derivatives of a density by the method of wavelets. Bull. Inform. Cybernet. 28 (1996) 91–100. Google Scholar
Schmisser, E., Non-parametric drift estimation for diffusions from noisy data. Stat. Decis. 28 (2011) 119–150. Google Scholar
G. Viennet, Inequalities for absolutely regular sequences : application to density estimation. Probab. Theory Relat. Fields (1997).