Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-29T21:16:59.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Penalization versus Goldenshluger − Lepski strategies in warped bases regression

Published online by Cambridge University Press:  17 May 2013

Gaëlle Chagny
Gaëlle Chagny*
Affiliation:
MAP5 UMR CNRS 8145, University Paris Descartes, 45 rue des Saints-Pères, 75006 Paris, France. gaelle.chagny@parisdescartes.fr
Get access

Abstract

This paper deals with the problem of estimating a regression function f, in a random design framework. We build and study two adaptive estimators based on model selection, applied with warped bases. We start with a collection of finite dimensional linear spaces, spanned by orthonormal bases. Instead of expanding directly the target function f on these bases, we rather consider the expansion of h = f ∘ G-1, where G is the cumulative distribution function of the design, following Kerkyacharian and Picard [Bernoulli 10 (2004) 1053–1105]. The data-driven selection of the (best) space is done with two strategies: we use both a penalization version of a “warped contrast”, and a model selection device in the spirit of Goldenshluger and Lepski [Ann. Stat. 39 (2011) 1608–1632]. We propose by these methods two functions, ĥl (l = 1, 2), easier to compute than least-squares estimators. We establish nonasymptotic mean-squared integrated risk bounds for the resulting estimators, \hbox{$\hat{f}_l=\hat{h}_l\circ G$}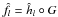f̂l = ĥl°G if G is known, or \hbox{$\hat{f}_l=\hat{h}_l\circ\hat{G}$}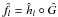f̂l = ĥl°Ĝ (l = 1,2) otherwise, where Ĝ is the empirical distribution function. We study also adaptive properties, in case the regression function belongs to a Besov or Sobolev space, and compare the theoretical and practical performances of the two selection rules.

Keywords

Adaptive estimatormodel selectionnonparametric regression estimationwarped bases
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 17 , 2013 , pp. 328 - 358
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antoniadis, A., Grégoire, G. and Vial, P., Random design wavelet curve smoothing. Statist. Probab. Lett. 35 (1997) 225–232. Google Scholar
J.Y. Audibert and O. Catoni, Robust linear least squares regression. Ann. Stat. (2011) (to appear), arXiv:1010.0074.
J.Y. Audibert and O. Catoni, Robust linear regression through PAC-Bayesian truncation. Preprint, arXiv:1010.0072.
Baraud, Y., Model selection for regression on a random design. ESAIM: PS 6 (2002) 127–146. Google Scholar
Barron, A., Birgé, L. and Massart, P., Risk bounds for model selection via penalization. Probab. Theory Relat. Fields 113 (1999) 301–413. Google Scholar
Baudry, J.P., Maugis, C. and Michel, B., Slope heuristics: overview and implementation. Stat. Comput. 22-2 (2011) 455–470.Google Scholar
Birgé, L., Model selection for Gaussian regression with random design. Bernoulli 10 (2004) 1039–1051. Google Scholar
Birgé, L. and Massart, P., Minimum contrast estimators on sieves: exponential bounds and rates of convergence. Bernoulli 4 (1998) 329–375. Google Scholar
Birgé, L. and Massart, P., Minimal penalties for gaussian model selection. Probab. Theory Relat. Fields 138 (2006) 33–73. Google Scholar
Brunel, E. and Comte, F., Penalized contrast estimation of density and hazard rate with censored data. Sankhya 67 (2005) 441–475. Google Scholar
Brunel, E., Comte, F. and Guilloux, A., Nonparametric density estimation in presence of bias and censoring. Test 18 (2009) 166–194. Google Scholar
Cai, T.T. and Brown, L.D., Wavelet shrinkage for nonequispaced samples. Ann. Stat. 26 (1998) 1783–1799. Google Scholar
G. Chagny, Régression: bases déformées et sélection de modèles par pénalisation et méthode de Lepski. Preprint, hal-00519556 v2.
Comte, F. and Rozenholc, Y., A new algorithm for fixed design regression and denoising. Ann. Inst. Stat. Math. 56 (2004) 449–473. Google Scholar
R.A. DeVore and G. Lorentz, Constructive approximation, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 303. Springer-Verlag, Berlin (1993).
Donoho, D.L., Johnstone, I.M., Kerkyacharian, G. and Picard, D., Wavelet shrinkage: asymptopia? With discussion and a reply by the authors. J. Roy. Stat. Soc., Ser. B 57 (1995) 301–369. Google Scholar
Dvoretzky, A., Kiefer, J. and Wolfowitz, J., Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. Ann. Math. Stat. 27 (1956) 642–669. Google Scholar
S. Efromovich, Nonparametric curve estimation: Methods, theory, and applications. Springer Series in Statistics, Springer-Verlag, New York (1999) xiv+411
Fan, J. and Gijbels, I., Variable bandwidth and local linear regression smoothers. Ann. Stat. 20 (1992) 2008–2036. Google Scholar
Gaïffas, S., On pointwise adaptive curve estimation based on inhomogeneous data. ESAIM: PS 11 (2007) 344–364. Google Scholar
Goldenshluger, A. and Lepski, O., Bandwidth selection in kernel density estimation: oracle inequalities and adaptive minimax optimality. Ann. Stat. 39 (2011) 1608–1632. Google Scholar
Golubev, G.K. and Nussbaum, M., Adaptive spline estimates in a nonparametric regression model. Teor. Veroyatnost. i Primenen. ( Russian) 37 (1992) 554–561; translation in Theor. Probab. Appl. 37 (1992) 521–529. Google Scholar
Härdle, W. and Tsybakov, A., Local polynomial estimators of the volatility function in nonparametric autoregression. J. Econ. 81 (1997) 223–242. Google Scholar
Kerkyacharian, G. and Picard, D., Regression in random design and warped wavelets. Bernoulli 10 (2004) 1053–1105. Google Scholar
Klein, T. and Rio, E., Concentration around the mean for maxima of empirical processes. Ann. Probab. 33 (2005) 1060–1077. Google Scholar
Köhler, M. and Krzyzak, A., Nonparametric regression estimation using penalized least squares. IEEE Trans. Inf. Theory 47 (2001) 3054–3058. Google Scholar
Lacour, C., Adaptive estimation of the transition density of a particular hidden Markov chain. J. Multivar. Anal. 99 (2008) 787–814. Google Scholar
Nadaraya, E., On estimating regression. Theory Probab. Appl. 9 (1964) 141–142. Google Scholar
Pham Ngoc, T.-M., Regression in random design and Bayesian warped wavelets estimators. Electron. J. Stat. 3 (2009) 1084–1112. Google Scholar
A.B. Tsybakov, Introduction à l’estimation non-paramétrique, Mathématiques & Applications (Berlin), vol. 41. Springer-Verlag, Berlin (2004).
Watson, G.S., Smooth regression analysis. Sankhya A 26 (1964) 359–372. Google Scholar
Wegkamp, M., Model selection in nonparametric regression. Ann. Stat. 31 (2003) 252–273. Google Scholar