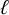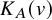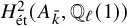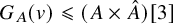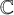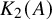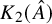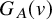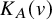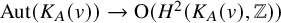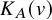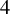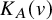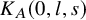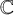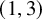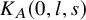1 Introduction
Given a polarized abelian surface
![]() $(A, H)$
defined over an arbitrary field k, we may study moduli spaces of geometrically H-stable sheaves on A with a fixed Mukai vector
$(A, H)$
defined over an arbitrary field k, we may study moduli spaces of geometrically H-stable sheaves on A with a fixed Mukai vector
![]() $v=(r,l,s)$
; that is, fixed rank, Néron-Severi class of the determinental line bundle and Euler characteristic. Under mild conditions on the Mukai vector, the moduli spaces
$v=(r,l,s)$
; that is, fixed rank, Néron-Severi class of the determinental line bundle and Euler characteristic. Under mild conditions on the Mukai vector, the moduli spaces
![]() $M_A(v)$
are smooth and projective. Their Albanese varieties are
$M_A(v)$
are smooth and projective. Their Albanese varieties are
![]() $A\times \hat {A}$
, and we denote a fiber of the Albanese morphism by
$A\times \hat {A}$
, and we denote a fiber of the Albanese morphism by
![]() $K_A(v)$
.
$K_A(v)$
.
If defined over
![]() ${\mathbb C}$
, the variety
${\mathbb C}$
, the variety
![]() $K_A(v)$
is a hyperkähler variety of dimension
$K_A(v)$
is a hyperkähler variety of dimension
![]() $v^2-2$
and is deformation equivalent to the generalized Kummer variety
$v^2-2$
and is deformation equivalent to the generalized Kummer variety
![]() $K_n(A)\cong K_A(1,0,-n-1)$
, where
$K_n(A)\cong K_A(1,0,-n-1)$
, where
![]() $n:=\frac {v^2}{2}-1$
, which is given by the fiber over
$n:=\frac {v^2}{2}-1$
, which is given by the fiber over
![]() $0$
of the summation map acting on the Hilbert scheme of length-
$0$
of the summation map acting on the Hilbert scheme of length-
![]() $(n+1)$
points on A. Following Fu and Li [Reference García and Lax17], who study these varieties over other fields, we call the
$(n+1)$
points on A. Following Fu and Li [Reference García and Lax17], who study these varieties over other fields, we call the
![]() $K_A(v)$
symplectic varieties (see Proposition 2.5). There are four known deformation types of hyperkähler varieties:
$K_A(v)$
symplectic varieties (see Proposition 2.5). There are four known deformation types of hyperkähler varieties:
![]() $\operatorname {\mathrm {K3}}^{[n]}$
-type, Kummer type (or
$\operatorname {\mathrm {K3}}^{[n]}$
-type, Kummer type (or
![]() $\operatorname {\mathrm {Kum}}_n$
-type) and the two sporadic examples of O’Grady [Reference O’Grady49, Reference Ploog50]. The varieties
$\operatorname {\mathrm {Kum}}_n$
-type) and the two sporadic examples of O’Grady [Reference O’Grady49, Reference Ploog50]. The varieties
![]() $K_A(v)$
are of Kummer n-type. It has been shown [Reference Mongardi and Wandel41, Prop. 2.4] that under a lattice-theoretic condition, if
$K_A(v)$
are of Kummer n-type. It has been shown [Reference Mongardi and Wandel41, Prop. 2.4] that under a lattice-theoretic condition, if
![]() $n+1$
is a prime power, any hyperkähler of Kummer n-type is the fiber of the Albanese map of a moduli space of stable objects on an abelian surface A. So varieties
$n+1$
is a prime power, any hyperkähler of Kummer n-type is the fiber of the Albanese map of a moduli space of stable objects on an abelian surface A. So varieties
![]() $K_A(v)$
do not exhaust the class but are, at this point, the best understood.
$K_A(v)$
do not exhaust the class but are, at this point, the best understood.
In [Reference Honigs21], Hassett and Tschinkel analyze the cohomology of complex generalized Kummer fourfolds
![]() $K_2(A)$
. They show that
$K_2(A)$
. They show that
![]() $H^4(K_2(A), {\mathbb Q})$
is generated by
$H^4(K_2(A), {\mathbb Q})$
is generated by
![]() $H^2(K_2(A),{\mathbb Q})$
and an
$H^2(K_2(A),{\mathbb Q})$
and an
![]() $81$
-dimensional vector space spanned by the cycle classes of
$81$
-dimensional vector space spanned by the cycle classes of
![]() $81$
distinct K3 surfaces in
$81$
distinct K3 surfaces in
![]() $K_2(A)$
. These surfaces are each contained in the fixed locus of a symplectic involution of the form
$K_2(A)$
. These surfaces are each contained in the fixed locus of a symplectic involution of the form
![]() $t_x^*\iota ^*$
, where
$t_x^*\iota ^*$
, where
![]() $\iota $
is multiplication by
$\iota $
is multiplication by
![]() $-1$
on A, and
$-1$
on A, and
![]() $t_x$
is translation by a point of the three-torsion
$t_x$
is translation by a point of the three-torsion
![]() $A[3]$
of A. Hassett and Tschinkel use deformation theory to show that the middle cohomology for any hyperkähler variety X of
$A[3]$
of A. Hassett and Tschinkel use deformation theory to show that the middle cohomology for any hyperkähler variety X of
![]() $\operatorname {\mathrm {Kum}}_2$
-type has a similar decomposition. The cohomology of Kummer-type hyperkähler varieties is also studied in [Reference Gulbrandsen19].
$\operatorname {\mathrm {Kum}}_2$
-type has a similar decomposition. The cohomology of Kummer-type hyperkähler varieties is also studied in [Reference Gulbrandsen19].
In this paper, we extend these results by characterizing the Galois action on the
![]() $\ell $
-adic étale cohomology of fourfolds
$\ell $
-adic étale cohomology of fourfolds
![]() $K_A(v)$
over nonclosed fields. As one might expect from the results of Hassett–Tschinkel, there is an
$K_A(v)$
over nonclosed fields. As one might expect from the results of Hassett–Tschinkel, there is an
![]() $81$
-dimensional subspace of
$81$
-dimensional subspace of
![]() $H^4_{\mathrm {\acute{e}t}}(K_2(A)_{\bar {k}},{{\mathbb Q}}_{\ell }(2))$
whose Galois action is determined by the structure of
$H^4_{\mathrm {\acute{e}t}}(K_2(A)_{\bar {k}},{{\mathbb Q}}_{\ell }(2))$
whose Galois action is determined by the structure of
![]() $A[3]$
. However, deformation-theoretic tools are too coarse to keep track of how the Galois action changes for other fourfolds
$A[3]$
. However, deformation-theoretic tools are too coarse to keep track of how the Galois action changes for other fourfolds
![]() $K_A(v)$
, which we find depends on v:
$K_A(v)$
, which we find depends on v:
Theorem 1.1 (Theorem 4.4, Proposition 4.6)
Suppose
![]() $K_A(v)$
is a smooth, projective variety over an arbitrary field k. Then, there is a subgroup
$K_A(v)$
is a smooth, projective variety over an arbitrary field k. Then, there is a subgroup
![]() $G_{A_{{\bar {k}}}}(v) \leqslant (A_{{\bar {k}}}\times \hat {A}_{{\bar {k}}})[3]$
and a Galois equivariant isomorphism
$G_{A_{{\bar {k}}}}(v) \leqslant (A_{{\bar {k}}}\times \hat {A}_{{\bar {k}}})[3]$
and a Galois equivariant isomorphism
where V is the
![]() $80$
-dimensional subrepresentation of the permutation representation
$80$
-dimensional subrepresentation of the permutation representation
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
and the trivial representation
![]() ${\mathbb Q}_{\ell }$
is the span of
${\mathbb Q}_{\ell }$
is the span of
![]() $(0,0)\in G_{A_{\bar {k}}}(v)$
. The Galois action on the group ring
$(0,0)\in G_{A_{\bar {k}}}(v)$
. The Galois action on the group ring
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
is induced by the action on
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
is induced by the action on
![]() $G_{A_{\bar {k}}}(v)$
.
$G_{A_{\bar {k}}}(v)$
.
By a generalization of the work of Yoshioka [Reference Yoshioka56], this means the Galois action on the middle cohomology is determined by the action on
![]() $H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))$
and the action on the subgroup
$H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))$
and the action on the subgroup
![]() $G_{A_{\bar {k}}}(v)$
, which is the kernel of the isogeny
$G_{A_{\bar {k}}}(v)$
, which is the kernel of the isogeny
![]() $\phi \colon A\times \hat {A} \to A\times \hat {A}$
given by
$\phi \colon A\times \hat {A} \to A\times \hat {A}$
given by
![]() $(x,y)\mapsto (\phi _M(y)-sx,\phi _L(x)+ry)$
(See Section 3.1). This stands in surprising contrast to the case of moduli spaces of sheaves on K3 surfaces – symplectic varieties of K3
$(x,y)\mapsto (\phi _M(y)-sx,\phi _L(x)+ry)$
(See Section 3.1). This stands in surprising contrast to the case of moduli spaces of sheaves on K3 surfaces – symplectic varieties of K3
![]() $^{[n]}$
-type – where the cohomology representations depend only on that of the K3 surface [Reference Frei, Honigs and Voight15, Thm. 2].
$^{[n]}$
-type – where the cohomology representations depend only on that of the K3 surface [Reference Frei, Honigs and Voight15, Thm. 2].
As a consequence, by studying the even cohomology of
![]() $K_2(A)$
for A defined over a number field, we are able to show the following result on derived equivalence:
$K_2(A)$
for A defined over a number field, we are able to show the following result on derived equivalence:
Corollary 1.2 (Corollary 5.8)
Let A be an abelian surface over a number field k for which the permutation representations associated to
![]() $A_{\bar {k}}[3]$
and
$A_{\bar {k}}[3]$
and
![]() $\hat {A}_{\bar {k}}[3]$
are not isomorphic. Then,
$\hat {A}_{\bar {k}}[3]$
are not isomorphic. Then,
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
are not derived equivalent over k.
$K_2(\hat {A})$
are not derived equivalent over k.
In forthcoming work [Reference Fu and Li16] on Galois actions on torsion subgroups of abelian surfaces, examples of such abelian surfaces are constructed. Intriguingly, this corollary shows that if
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
are derived equivalent after base change to
$K_2(\hat {A})$
are derived equivalent after base change to
![]() ${\mathbb C}$
, then the kernel of the Fourier–Mukai transform cannot be given by naturally associated bundles that would descend to the field of definition for A. Corollary 1.2 complements the recent work of Magni [Reference Markman37], which provides a sufficient condition for the existence of such equivalences over algebraically closed fields of characteristic zero.
${\mathbb C}$
, then the kernel of the Fourier–Mukai transform cannot be given by naturally associated bundles that would descend to the field of definition for A. Corollary 1.2 complements the recent work of Magni [Reference Markman37], which provides a sufficient condition for the existence of such equivalences over algebraically closed fields of characteristic zero.
The cohomology group V in Theorem 1.1 is generated by K3 surfaces contained in the fixed-point loci of symplectic involutions on
![]() $K_A(v)$
. We give a case-by-case explicit description of
$K_A(v)$
. We give a case-by-case explicit description of
![]() $G_A(v)$
, and hence, an explicit description of these symplectic involutions, which dictate the Galois action on V.
$G_A(v)$
, and hence, an explicit description of these symplectic involutions, which dictate the Galois action on V.
By work of Boissière–Nieper-Wisskirchen–Sarti in [Reference Bolognesi and Massarenti8], Hassett–Tschinkel in [Reference Honigs21] and Kapfer–Menet in [Reference Kass31], for any hyperkähler variety X over
![]() ${\mathbb C}$
of
${\mathbb C}$
of
![]() $\operatorname {\mathrm {Kum}}_{n-1}$
-type, the kernel
$\operatorname {\mathrm {Kum}}_{n-1}$
-type, the kernel
consists of symplectic automorphisms of X; when
![]() $\dim X=4$
, the kernel contains all of the symplectic involutions of X. We give an explicit description of this kernel for hyperkähler varieties
$\dim X=4$
, the kernel contains all of the symplectic involutions of X. We give an explicit description of this kernel for hyperkähler varieties
![]() $K_A(v)$
of any dimension at least
$K_A(v)$
of any dimension at least
![]() $4$
over
$4$
over
![]() ${\mathbb C}$
.
${\mathbb C}$
.
Theorem 1.3 (Theorem 3.15)
Suppose
![]() $K_A(v)$
is a smooth, projective variety over
$K_A(v)$
is a smooth, projective variety over
![]() $k={\mathbb C}$
. Then,
$k={\mathbb C}$
. Then,
consists of automorphisms of the following two forms:
where
![]() $\kappa =\iota ^*$
if
$\kappa =\iota ^*$
if
![]() $K_A(v)$
is an Albanese fiber over symmetric line bundles, and otherwise
$K_A(v)$
is an Albanese fiber over symmetric line bundles, and otherwise
![]() $\kappa $
is a composition of
$\kappa $
is a composition of
![]() $\iota ^*$
with a translation. The
$\iota ^*$
with a translation. The
![]() $\kappa _{(x,y)}$
are symplectic involutions of
$\kappa _{(x,y)}$
are symplectic involutions of
![]() $K_A(v)$
, and when
$K_A(v)$
, and when
![]() $\dim K_A(v)=4$
, these are all of the symplectic involutions.
$\dim K_A(v)=4$
, these are all of the symplectic involutions.
In the complex case, the group
![]() $G_{A}(v)$
also appears in [Reference Matsushita38] as
$G_{A}(v)$
also appears in [Reference Matsushita38] as
![]() $\Gamma _v$
. Markman defines
$\Gamma _v$
. Markman defines
![]() $\Gamma _v$
as the kernel of the map
$\Gamma _v$
as the kernel of the map
![]() $\phi $
above as well as in terms of Clifford algebras (§10.1, Remark 4.3 op.cit.). The result [Reference Matsushita38, Lemma 10.1] and its proof show
$\phi $
above as well as in terms of Clifford algebras (§10.1, Remark 4.3 op.cit.). The result [Reference Matsushita38, Lemma 10.1] and its proof show
![]() $\Gamma _v$
embeds into the monodromy group of
$\Gamma _v$
embeds into the monodromy group of
![]() $K_A(v)$
, acts trivially on
$K_A(v)$
, acts trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
and
$H^2(K_A(v),{\mathbb Z})$
and
![]() $H^3(K_A(v),{\mathbb Z})$
, and that
$H^3(K_A(v),{\mathbb Z})$
, and that
![]() $M_A(v)$
is isomorphic to a quotient of
$M_A(v)$
is isomorphic to a quotient of
![]() $A\times \hat {A}\times K_A(v)$
by an action of
$A\times \hat {A}\times K_A(v)$
by an action of
![]() $\Gamma _v$
. Thus, the fact that the automorphisms
$\Gamma _v$
. Thus, the fact that the automorphisms
![]() $L_y\otimes t_x^*$
are symplectic is not new, but we provide a proof to make our study of this family self-contained.
$L_y\otimes t_x^*$
are symplectic is not new, but we provide a proof to make our study of this family self-contained.
Beyond their analysis of the middle cohomology for
![]() $K_2(A)$
, Hassett and Tschinkel explicitly describe the fixed-point loci of the symplectic involutions. They show that the locus fixed by the standard involution contains the Kummer K3 surface
$K_2(A)$
, Hassett and Tschinkel explicitly describe the fixed-point loci of the symplectic involutions. They show that the locus fixed by the standard involution contains the Kummer K3 surface
as well as a unique isolated point supported at the identity element
![]() $0$
. Tarí in [Reference Tarí54] finishes the description by showing there are 35 more isolated points, which are tuples of two-torsion points of A. The deformation invariance of the symplectic involutions implies that the fixed locus of any
$0$
. Tarí in [Reference Tarí54] finishes the description by showing there are 35 more isolated points, which are tuples of two-torsion points of A. The deformation invariance of the symplectic involutions implies that the fixed locus of any
![]() $\iota _{(x,y)}$
in
$\iota _{(x,y)}$
in
![]() $K_A(v)$
also consists of a K3 surface and 36 isolated points [Reference Kass31, Thm. 7.5].
$K_A(v)$
also consists of a K3 surface and 36 isolated points [Reference Kass31, Thm. 7.5].
Motivated by these results, we seek a similar description of the fixed-point loci in fourfolds
![]() $K_A(0,l,s)$
, whose general member is a degree
$K_A(0,l,s)$
, whose general member is a degree
![]() $s+3$
line bundle on a genus 4 curve in the linear system
$s+3$
line bundle on a genus 4 curve in the linear system
![]() $|L|$
with
$|L|$
with
![]() $c_1(L)=l$
. These moduli spaces admit a Lagrangian fibration, which aids in our study. We give the following description:
$c_1(L)=l$
. These moduli spaces admit a Lagrangian fibration, which aids in our study. We give the following description:
Theorem 1.4 (Theorem 7.2)
The K3 surface in the fixed-point locus of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $K_A(0,l,s)$
is elliptically fibered with four singular fibers of type
$K_A(0,l,s)$
is elliptically fibered with four singular fibers of type
![]() $I_1$
and
$I_1$
and
![]() $10$
singular fibers of type
$10$
singular fibers of type
![]() $I_2$
.
$I_2$
.
The singular fibers in this elliptic fibration agree with a natural elliptic fibration on the Kummer K3 surface
![]() $K_1(A)$
when A is
$K_1(A)$
when A is
![]() $(1,3)$
-polarized – a necessary condition for
$(1,3)$
-polarized – a necessary condition for
![]() $K_A(0,l,s)$
to be a fourfold. The K3 surface appears to be closely connected to the relative Jacobian of
$K_A(0,l,s)$
to be a fourfold. The K3 surface appears to be closely connected to the relative Jacobian of
![]() $K_1(A)\to {\mathbb P}^1$
.
$K_1(A)\to {\mathbb P}^1$
.
We also describe the isolated points in the fixed-point locus using the Abel map for the curves in
![]() $|L|$
.
$|L|$
.
Outline
In Section 2, we provide a brief introduction to moduli spaces of sheaves, and Kummer-type varieties arising from them, over arbitrary fields. In Section 3, we identify which automorphisms of
![]() $M_A(v)$
given by translation and tensoring by a degree 0 line bundle restrict to automorphisms of
$M_A(v)$
given by translation and tensoring by a degree 0 line bundle restrict to automorphisms of
![]() $K_A(v)$
, and then show how these give rise to the description of the symplectic automorphisms discussed in Theorem 1.3. We also begin the analysis of the fixed-point loci for the symplectic involutions. In Section 4, we study the middle cohomology of fourfolds
$K_A(v)$
, and then show how these give rise to the description of the symplectic automorphisms discussed in Theorem 1.3. We also begin the analysis of the fixed-point loci for the symplectic involutions. In Section 4, we study the middle cohomology of fourfolds
![]() $K_A(v)$
, proving Theorem 1.1. In Section 5, we compare our results to questions about derived equivalences between abelian surfaces and their generalized Kummer fourfolds. Namely, we give criteria in Section 5.1 for when a derived equivalence between abelian surfaces A and B induces an isomorphism between
$K_A(v)$
, proving Theorem 1.1. In Section 5, we compare our results to questions about derived equivalences between abelian surfaces and their generalized Kummer fourfolds. Namely, we give criteria in Section 5.1 for when a derived equivalence between abelian surfaces A and B induces an isomorphism between
![]() $G_A(v)$
and
$G_A(v)$
and
![]() $G_B(v)$
, and we prove Corollary 1.2 in Section 5.2.
$G_B(v)$
, and we prove Corollary 1.2 in Section 5.2.
The second half of the paper is dedicated to studying the fixed-point locus of
![]() $\iota ^*$
for fourfolds
$\iota ^*$
for fourfolds
![]() $K_A(0,l,s)$
over
$K_A(0,l,s)$
over
![]() ${\mathbb C}$
, including the proof of Theorem 1.4. In Section 6, we study the general geometry of
${\mathbb C}$
, including the proof of Theorem 1.4. In Section 6, we study the general geometry of
![]() $K_A(0,l,s)$
and the fixed-point locus, and then focus on the elliptic fibers of the K3 surface in Section 7. In Section 8, we describe the isolated points in the fixed-point locus.
$K_A(0,l,s)$
and the fixed-point locus, and then focus on the elliptic fibers of the K3 surface in Section 7. In Section 8, we describe the isolated points in the fixed-point locus.
Notation
We write the standard involution on an abelian surface A, the morphism multiplying by
![]() $-1$
in the group law of A, as
$-1$
in the group law of A, as
![]() $\iota \colon A\to A$
. We write
$\iota \colon A\to A$
. We write
![]() $K_n(A)$
for the generalized Kummer variety of dimension
$K_n(A)$
for the generalized Kummer variety of dimension
![]() $2n$
. In particular, we write
$2n$
. In particular, we write
![]() $K_1(A)$
for the Kummer K3 surface of A.
$K_1(A)$
for the Kummer K3 surface of A.
For a smooth projective variety X over a field k, let
![]() $X_{{\bar {k}}}:=X\times _k {\bar {k}}$
. We denote by
$X_{{\bar {k}}}:=X\times _k {\bar {k}}$
. We denote by
![]() $\widetilde {H}(X_{{\bar {k}}},{\mathbb Z}_{\ell })$
the
$\widetilde {H}(X_{{\bar {k}}},{\mathbb Z}_{\ell })$
the
![]() $\ell $
-adic Mukai lattice of X, which is the direct sum of the even cohomology twisted into weight zero:
$\ell $
-adic Mukai lattice of X, which is the direct sum of the even cohomology twisted into weight zero:
This lattice is given the usual Mukai pairing. For
![]() $X=A$
an abelian surface,
$X=A$
an abelian surface,
![]() $(\alpha , \beta ) =-\alpha _0\beta _4+\alpha _2\beta _2-\alpha _4\beta _0$
. We will always assume that our Mukai vectors v satisfy the conditions given in Setting 2.4 unless indicated otherwise.
$(\alpha , \beta ) =-\alpha _0\beta _4+\alpha _2\beta _2-\alpha _4\beta _0$
. We will always assume that our Mukai vectors v satisfy the conditions given in Setting 2.4 unless indicated otherwise.
Throughout,
![]() $D(X)$
denotes the bounded derived category of coherent sheaves on X.
$D(X)$
denotes the bounded derived category of coherent sheaves on X.
2 Moduli spaces over arbitrary fields
Let A be an abelian surface defined over an arbitrary field k.
Definition 2.1. Let
![]() $\omega \in H^4_{\mathrm {\acute{e}t}}(A_{{\bar {k}}}, {\mathbb Z}_{\ell }(2))$
be the numerical equivalence class of a point on
$\omega \in H^4_{\mathrm {\acute{e}t}}(A_{{\bar {k}}}, {\mathbb Z}_{\ell }(2))$
be the numerical equivalence class of a point on
![]() $A_{{\bar {k}}}$
. A Mukai vector on A is an element of
$A_{{\bar {k}}}$
. A Mukai vector on A is an element of
where
![]() $N(A)$
is a subgroup of
$N(A)$
is a subgroup of
![]() $\widetilde {H}(A_{{\bar {k}}}, {\mathbb Z}_{\ell })$
under the natural inclusion.
$\widetilde {H}(A_{{\bar {k}}}, {\mathbb Z}_{\ell })$
under the natural inclusion.
Given a coherent sheaf
![]() $\mathcal F$
on A, we assign to it a Mukai vector
$\mathcal F$
on A, we assign to it a Mukai vector
![]() $v(\mathcal F)\in N(A)$
given by its rank, the Néron-Severi class of its determinantal line bundle and its Euler characteristic. We will write this as
$v(\mathcal F)\in N(A)$
given by its rank, the Néron-Severi class of its determinantal line bundle and its Euler characteristic. We will write this as
![]() $v(\mathcal F)=(r,l,s)$
.
$v(\mathcal F)=(r,l,s)$
.
By fixing a Mukai vector v and a polarization H on A, we can construct the moduli space
![]() $M_{A,H}(v)$
parametrizing H-semistable sheaves on A. We use the more compact notation
$M_{A,H}(v)$
parametrizing H-semistable sheaves on A. We use the more compact notation
![]() $M_A(v)$
. We ask that the Mukai vector satisfies the following conditions in order to ensure that the moduli space is nicely behaved (i.e., is a nonempty, smooth, projective variety over k).
$M_A(v)$
. We ask that the Mukai vector satisfies the following conditions in order to ensure that the moduli space is nicely behaved (i.e., is a nonempty, smooth, projective variety over k).
Definition 2.2.
-
(a) A Mukai vector
 $v \in N(A)$
is geometrically primitive if its image under
$v \in N(A)$
is geometrically primitive if its image under
 ${N(A) \to N(A_{{\bar {k}}})}$
is primitive in the lattice.
${N(A) \to N(A_{{\bar {k}}})}$
is primitive in the lattice. -
(b) A Mukai vector
 $(r,l,s)$
is positive if one of the following is satisfied:
$(r,l,s)$
is positive if one of the following is satisfied:-
(i)
 $r>0$
$r>0$
-
(ii)
 $r=0$
, l is effective and
$r=0$
, l is effective and
 $s\neq 0$
$s\neq 0$
-
(iii)
 $r=0$
,
$r=0$
,
 $l=0$
and
$l=0$
and
 $s<0$
.
$s<0$
.
-
-
(c) A polarization
 $H\in \mathrm {Pic}(A)$
is v-generic if every H-semistable sheaf with Mukai vector v defined over
$H\in \mathrm {Pic}(A)$
is v-generic if every H-semistable sheaf with Mukai vector v defined over
 ${\bar {k}}$
is H-stable.
${\bar {k}}$
is H-stable.
A polarization is often v-generic if it is not contained in a locally finite union of certain hyperplanes in
![]() $\operatorname {\mathrm {NS}}(A_{\bar {k}})_{\mathbb R}$
defined in [Reference Kaledin, Lehn and Sorger28, Def. 4.C.1], but this is not always enough to ensure genericity (see, for example, [Reference Frei, Honigs and Voight15, Ex. 1.7]).
$\operatorname {\mathrm {NS}}(A_{\bar {k}})_{\mathbb R}$
defined in [Reference Kaledin, Lehn and Sorger28, Def. 4.C.1], but this is not always enough to ensure genericity (see, for example, [Reference Frei, Honigs and Voight15, Ex. 1.7]).
When
![]() $v^2=0$
and H is v-generic, Mukai showed that
$v^2=0$
and H is v-generic, Mukai showed that
![]() $M_H(v)$
is an abelian surface [Reference Mumford46, Rmk. 5.13]. We focus on the higher-dimensional case.
$M_H(v)$
is an abelian surface [Reference Mumford46, Rmk. 5.13]. We focus on the higher-dimensional case.
Proposition 2.3. Let
![]() $v\in N(A)$
be a geometrically primitive and positive Mukai vector with
$v\in N(A)$
be a geometrically primitive and positive Mukai vector with
![]() $v^2\geq 2$
, and let H be a v-generic polarization on A. Then,
$v^2\geq 2$
, and let H be a v-generic polarization on A. Then,
![]() $M_A(v)$
is a nonempty, smooth, projective, geometrically irreducible variety of dimension
$M_A(v)$
is a nonempty, smooth, projective, geometrically irreducible variety of dimension
![]() $v^2+2$
over k.
$v^2+2$
over k.
Proof. The projectivity and smoothness are shown in [Reference García and Lax17, Prop. 6.9], which relies on classic results in [Reference Mukai44] as well as [Reference Li and Zou34] for the construction of moduli spaces of semistable sheaves over arbitrary fields. Geometric irreducibility of
![]() $M_A(v)$
follows from [Reference Kamenova, Mongardi and Oblomkov29, Thm. 4.1] (note that the authors work over
$M_A(v)$
follows from [Reference Kamenova, Mongardi and Oblomkov29, Thm. 4.1] (note that the authors work over
![]() ${\mathbb C}$
, but their proof holds for any algebraically closed field). Finally, the dimension claim follows from [Reference Mukai44, Cor. 0.2] once we know
${\mathbb C}$
, but their proof holds for any algebraically closed field). Finally, the dimension claim follows from [Reference Mukai44, Cor. 0.2] once we know
![]() $M_A(v)$
is nonempty; nonemptiness is a consequence of [Reference Yoshioka56, Thm. 0.1] along with a lifting argument as in [Reference García and Lax17, Prop. 6.9] when the field has positive characteristic.
$M_A(v)$
is nonempty; nonemptiness is a consequence of [Reference Yoshioka56, Thm. 0.1] along with a lifting argument as in [Reference García and Lax17, Prop. 6.9] when the field has positive characteristic.
Let
![]() $v:=(r,l,s)$
be a Mukai vector as in Proposition 2.3 and let
$v:=(r,l,s)$
be a Mukai vector as in Proposition 2.3 and let
denote the Fourier–Mukai transform on A, which has kernel the Poincaré bundle P on
![]() $A \times \hat {A}$
. In [Reference Yoshioka56, Thm. 4.1], Yoshioka proves over
$A \times \hat {A}$
. In [Reference Yoshioka56, Thm. 4.1], Yoshioka proves over
![]() ${\mathbb C}$
that the Albanese variety of
${\mathbb C}$
that the Albanese variety of
![]() $M_H(v)$
is
$M_H(v)$
is
![]() $A\times \hat {A}$
and fixing any
$A\times \hat {A}$
and fixing any
![]() $\mathcal F_0\in M_H(v)$
, we define the Albanese morphism as follows:
$\mathcal F_0\in M_H(v)$
, we define the Albanese morphism as follows:
 $$ \begin{align} M_A(v) &\to \hat{A}\times A\\ \mathcal F &\mapsto (\det(\mathcal F)\otimes \det(\mathcal F_0)^{-1}, \det(\Phi_P(\mathcal F))\otimes \det(\Phi_P(\mathcal F_0))^{-1})\notag \end{align} $$
$$ \begin{align} M_A(v) &\to \hat{A}\times A\\ \mathcal F &\mapsto (\det(\mathcal F)\otimes \det(\mathcal F_0)^{-1}, \det(\Phi_P(\mathcal F))\otimes \det(\Phi_P(\mathcal F_0))^{-1})\notag \end{align} $$
This construction also shows that over an arbitrary field k, the following map gives the Albanese torsor of
![]() $M_H(v)$
:
$M_H(v)$
:
 $$ \begin{align} \operatorname{\mathrm{alb}}\colon M_A(v) &\to \operatorname{\mathrm{Pic}}^l_A\times\operatorname{\mathrm{Pic}}^{m}_{\hat{A}}\\ \mathcal F &\mapsto (\det(\mathcal F),\det(\Phi_P(\mathcal F))),\notag \end{align} $$
$$ \begin{align} \operatorname{\mathrm{alb}}\colon M_A(v) &\to \operatorname{\mathrm{Pic}}^l_A\times\operatorname{\mathrm{Pic}}^{m}_{\hat{A}}\\ \mathcal F &\mapsto (\det(\mathcal F),\det(\Phi_P(\mathcal F))),\notag \end{align} $$
where m is the Néron-Severi class in the Mukai vector
![]() $\Phi _P(v):=(s,m,r)$
, which is the negative of the Poincaré dual of l by [Reference Mukai45, Prop. 1.17].
$\Phi _P(v):=(s,m,r)$
, which is the negative of the Poincaré dual of l by [Reference Mukai45, Prop. 1.17].
Setting 2.4. Let A be an abelian surface defined over a field k. Let
![]() $v:=(r,l,s)\in N(A)$
be a geometrically primitive and positive Mukai vector with
$v:=(r,l,s)\in N(A)$
be a geometrically primitive and positive Mukai vector with
![]() $v^2\geq 6$
and
$v^2\geq 6$
and
![]() $\operatorname {\mathrm {char}} k \nmid \frac {v^2}{2}$
. Let H be a v-generic polarization on A. Fix
$\operatorname {\mathrm {char}} k \nmid \frac {v^2}{2}$
. Let H be a v-generic polarization on A. Fix
![]() $(L,M)$
a pair of line bundles in
$(L,M)$
a pair of line bundles in
![]() $\operatorname {\mathrm {Pic}}^l(A)\times \operatorname {\mathrm {Pic}}^{m}(\hat {A})$
. Let
$\operatorname {\mathrm {Pic}}^l(A)\times \operatorname {\mathrm {Pic}}^{m}(\hat {A})$
. Let
![]() $K_A(v)$
be the fiber of
$K_A(v)$
be the fiber of
![]() $\operatorname {\mathrm {alb}}$
over
$\operatorname {\mathrm {alb}}$
over
![]() $(L,M)$
.
$(L,M)$
.
Over
![]() ${\mathbb C}$
, [Reference Yoshioka56, Thm. 0.2] shows that
${\mathbb C}$
, [Reference Yoshioka56, Thm. 0.2] shows that
![]() $K_A(v)$
is a hyperhähler variety, and the following result generalizes this to other fields.
$K_A(v)$
is a hyperhähler variety, and the following result generalizes this to other fields.
Proposition 2.5 [Reference Yoshioka56, Thm. 0.2], [Reference García and Lax17, Prop. 6.9]
Suppose we have data as in Setting 2.4. Then,
![]() $K_A(v)$
is a smooth, projective symplectic variety of dimension
$K_A(v)$
is a smooth, projective symplectic variety of dimension
![]() $v^2-2$
and is deformation equivalent to the generalized Kummer variety
$v^2-2$
and is deformation equivalent to the generalized Kummer variety
![]() $K_{(v^2-2)/2}(A)$
.
$K_{(v^2-2)/2}(A)$
.
For
![]() $K_A(v)$
over a field of characteristic zero, which we may assume is a subfield of
$K_A(v)$
over a field of characteristic zero, which we may assume is a subfield of
![]() ${\mathbb C}$
,
${\mathbb C}$
,
![]() $K_A(v)_{\mathbb C}$
is a hyperkähler variety. In positive characteristic, Fu and Li [Reference García and Lax17, Def. 3.1] define a symplectic variety X to be a smooth connected variety, where
$K_A(v)_{\mathbb C}$
is a hyperkähler variety. In positive characteristic, Fu and Li [Reference García and Lax17, Def. 3.1] define a symplectic variety X to be a smooth connected variety, where
![]() $\pi _1^{\mathrm {\acute{e}t}}(X)=0$
and X admits a nowhere degenerate closed algebraic
$\pi _1^{\mathrm {\acute{e}t}}(X)=0$
and X admits a nowhere degenerate closed algebraic
![]() $2$
-form.
$2$
-form.
We are interested in symplectic involutions on
![]() $K_A(v)$
. We will show in Theorem 3.15 that these all involve the induced action of the standard involution
$K_A(v)$
. We will show in Theorem 3.15 that these all involve the induced action of the standard involution
![]() $\iota $
on A. Pullback
$\iota $
on A. Pullback
![]() $\iota ^*$
sends degree
$\iota ^*$
sends degree
![]() $0$
line bundles on A to their inverses. For any line bundle
$0$
line bundles on A to their inverses. For any line bundle
![]() $\mathcal L\in \operatorname {\mathrm {Pic}}(A)$
, the multiplication by n map has the property that
$\mathcal L\in \operatorname {\mathrm {Pic}}(A)$
, the multiplication by n map has the property that
![]() $[n]^*\mathcal L\cong \mathcal L^{n^2}\otimes M$
for some
$[n]^*\mathcal L\cong \mathcal L^{n^2}\otimes M$
for some
![]() $M\in \operatorname {\mathrm {Pic}}^0(A)$
. Thus,
$M\in \operatorname {\mathrm {Pic}}^0(A)$
. Thus,
![]() $\mathcal L$
and
$\mathcal L$
and
![]() $\iota ^*\mathcal L$
differ by a degree
$\iota ^*\mathcal L$
differ by a degree
![]() $0$
line bundle, so are always in the same Néron-Severi class.
$0$
line bundle, so are always in the same Néron-Severi class.
In order for
![]() $\iota ^*$
to give a well-defined morphism on
$\iota ^*$
to give a well-defined morphism on
![]() $K_A(v)$
,
$K_A(v)$
,
![]() $K_A(v)$
must be a fiber of the Albanese morphism over a pair of symmetric line bundles L and M, which we prefer to do when possible for notational simplicity. In the case of generalized Kummer varieties
$K_A(v)$
must be a fiber of the Albanese morphism over a pair of symmetric line bundles L and M, which we prefer to do when possible for notational simplicity. In the case of generalized Kummer varieties
![]() $K_{n-1}(A)$
or varieties
$K_{n-1}(A)$
or varieties
![]() $K_A(v)$
whose Mukai vector has trivial Néron-Severi class, it is always possible to choose the fiber over the structure sheaves of A and
$K_A(v)$
whose Mukai vector has trivial Néron-Severi class, it is always possible to choose the fiber over the structure sheaves of A and
![]() $\hat {A}$
. For other choices of Mukai vector, we show in Lemma 2.6 below that over an algebraically closed field, we may always choose such a pair of symmetric line bundles.
$\hat {A}$
. For other choices of Mukai vector, we show in Lemma 2.6 below that over an algebraically closed field, we may always choose such a pair of symmetric line bundles.
Lemma 2.6. Let A be an abelian variety over an algebraically closed field k. Then, any class in
![]() $\operatorname {\mathrm {NS}}(A)$
has a symmetric representative. Moreover, there is a short exact sequence of the following form, where
$\operatorname {\mathrm {NS}}(A)$
has a symmetric representative. Moreover, there is a short exact sequence of the following form, where
![]() $\operatorname {\mathrm {Pic}}^{\operatorname {\mathrm {sym}}}(A)$
is the subgroup of all symmetric line bundles:
$\operatorname {\mathrm {Pic}}^{\operatorname {\mathrm {sym}}}(A)$
is the subgroup of all symmetric line bundles:
Proof. The action of
![]() $\iota ^*$
on the following short exact sequence
$\iota ^*$
on the following short exact sequence
gives rise to the long exact sequence
where
![]() $\operatorname {\mathrm {NS}}^{\operatorname {\mathrm {sym}}}(A)=\operatorname {\mathrm {NS}}(A)$
since, for any line bundle
$\operatorname {\mathrm {NS}}^{\operatorname {\mathrm {sym}}}(A)=\operatorname {\mathrm {NS}}(A)$
since, for any line bundle
![]() $\mathcal L$
,
$\mathcal L$
,
![]() $\iota ^*\mathcal L$
is in the same Néron-Severi class as
$\iota ^*\mathcal L$
is in the same Néron-Severi class as
![]() $\mathcal L$
. The group
$\mathcal L$
. The group
![]() $H^1({\mathbb Z}/2{\mathbb Z}, \operatorname {\mathrm {Pic}}^0(A))$
is trivial since crossed homomorphisms correspond to elements in
$H^1({\mathbb Z}/2{\mathbb Z}, \operatorname {\mathrm {Pic}}^0(A))$
is trivial since crossed homomorphisms correspond to elements in
![]() $\operatorname {\mathrm {Pic}}^0(A)$
and principal crossed homomorphisms correspond to choices of element in
$\operatorname {\mathrm {Pic}}^0(A)$
and principal crossed homomorphisms correspond to choices of element in
![]() $\operatorname {\mathrm {Pic}}^0(A)$
that have a square root, which is all of them, since we are working over an algebraically closed field.
$\operatorname {\mathrm {Pic}}^0(A)$
that have a square root, which is all of them, since we are working over an algebraically closed field.
The proof above requires the field k to be algebraically closed, but we will often work over a nonclosed field. In that case, the existence of a symmetric line bundle in a given Néron-Severi class is not guaranteed. Rather than working over a finite extension of the ground field in order to acquire a symmetric bundle, we will simply alter
![]() $\iota ^*$
by a correction factor to get an associated involution on
$\iota ^*$
by a correction factor to get an associated involution on
![]() $K_A(v)$
(see Construction 3.10).
$K_A(v)$
(see Construction 3.10).
3 Symplectic involutions on
 $K_A(v)$
$K_A(v)$
In [Reference Bolognesi and Massarenti8, Cor. 5(2)], the authors show that, for
![]() $X=K_{n-1}(A)$
over
$X=K_{n-1}(A)$
over
![]() ${\mathbb C}$
, the kernel of
${\mathbb C}$
, the kernel of
is isomorphic to
![]() ${\mathbb Z}/2{\mathbb Z} \ltimes ({\mathbb Z}/n{\mathbb Z})^4$
, generated by
${\mathbb Z}/2{\mathbb Z} \ltimes ({\mathbb Z}/n{\mathbb Z})^4$
, generated by
![]() $\iota $
and translation by elements of
$\iota $
and translation by elements of
![]() $A[n]$
. In fact, this group of automorphisms is isomorphic to
$A[n]$
. In fact, this group of automorphisms is isomorphic to
![]() ${\mathbb Z}/2{\mathbb Z} \ltimes ({\mathbb Z}/n{\mathbb Z})^4$
for any hyperkähler variety X of
${\mathbb Z}/2{\mathbb Z} \ltimes ({\mathbb Z}/n{\mathbb Z})^4$
for any hyperkähler variety X of
![]() $\operatorname {\mathrm {Kum}}_{n-1}$
-type, since it is a deformation invariant [Reference Honigs21, Thm. 2.1]. Moreover, when
$\operatorname {\mathrm {Kum}}_{n-1}$
-type, since it is a deformation invariant [Reference Honigs21, Thm. 2.1]. Moreover, when
![]() $\dim X=4$
,
$\dim X=4$
,
![]() $\ker \nu $
contains all of the symplectic involutions [Reference Kass31, Thm. 7.5(i)]. Markman identifies a subgroup
$\ker \nu $
contains all of the symplectic involutions [Reference Kass31, Thm. 7.5(i)]. Markman identifies a subgroup
![]() $\Gamma _v\cong ({\mathbb Z}/n{\mathbb Z})^4$
of
$\Gamma _v\cong ({\mathbb Z}/n{\mathbb Z})^4$
of
![]() $\ker \nu $
when
$\ker \nu $
when
![]() $X=K_A(v)$
as coming from the kernel of
$X=K_A(v)$
as coming from the kernel of
![]() $\phi $
defined below [Reference Matsushita38, §10.1]. In this section, we give an explicit description of
$\phi $
defined below [Reference Matsushita38, §10.1]. In this section, we give an explicit description of
![]() $\ker \nu $
for
$\ker \nu $
for
![]() $K_{A}(v)_{\bar {k}}$
when we are in the more general Setting 2.4 and k is arbitrary; this will allow us to understand the action of the Galois group on the fixed-point loci of the involutions in
$K_{A}(v)_{\bar {k}}$
when we are in the more general Setting 2.4 and k is arbitrary; this will allow us to understand the action of the Galois group on the fixed-point loci of the involutions in
![]() $\ker \nu $
.
$\ker \nu $
.
In Section 3.1, we identify which automorphisms of
![]() $M_A(v)$
given by translation and tensoring by a degree 0 line bundle restrict to automorphisms of
$M_A(v)$
given by translation and tensoring by a degree 0 line bundle restrict to automorphisms of
![]() $K_A(v)$
and show they form a group isomorphic to
$K_A(v)$
and show they form a group isomorphic to
![]() $({\mathbb Z}/n{\mathbb Z})^4$
. We also identify the group of such automorphisms when v is not primitive. The other automorphism needed to generate
$({\mathbb Z}/n{\mathbb Z})^4$
. We also identify the group of such automorphisms when v is not primitive. The other automorphism needed to generate
![]() $\ker \nu $
is
$\ker \nu $
is
![]() $\iota ^*$
when
$\iota ^*$
when
![]() $K_A(v)$
is the Albanese fiber over symmetric line bundles; in Section 3.2, we produce an involution
$K_A(v)$
is the Albanese fiber over symmetric line bundles; in Section 3.2, we produce an involution
![]() $\kappa $
to replace
$\kappa $
to replace
![]() $\iota ^*$
in the more general setting. We then study the fixed loci of the compositions of
$\iota ^*$
in the more general setting. We then study the fixed loci of the compositions of
![]() $\kappa $
with the automorphisms produced in Section 3.1. In Section 3.3, we show that these compositions are symplectic and act trivially on
$\kappa $
with the automorphisms produced in Section 3.1. In Section 3.3, we show that these compositions are symplectic and act trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
.
$H^2(K_A(v),{\mathbb Z})$
.
3.1 Automorphisms from translation and tensor
In this section, we work with data as in Setting 2.4, with the additional assumption that k is an algebraically closed field, and we define
![]() $n:=\frac {v^2}{2}$
. Because
$n:=\frac {v^2}{2}$
. Because
![]() $k=\bar {k}$
and
$k=\bar {k}$
and
![]() $\operatorname {\mathrm {char}} k \nmid n$
, we have
$\operatorname {\mathrm {char}} k \nmid n$
, we have
![]() $A[n]\cong ({\mathbb Z}/n{\mathbb Z})^{4}$
.
$A[n]\cong ({\mathbb Z}/n{\mathbb Z})^{4}$
.
We recall that given a line bundle
![]() $\mathcal {L}\in \operatorname {\mathrm {Pic}}(A)$
,
$\mathcal {L}\in \operatorname {\mathrm {Pic}}(A)$
,
![]() $\phi _{\mathcal L}\colon A\to \hat {A}$
is defined by
$\phi _{\mathcal L}\colon A\to \hat {A}$
is defined by
![]() $\phi _{\mathcal L}(x):=t_x^*\mathcal L\otimes \mathcal L^{-1}$
, where
$\phi _{\mathcal L}(x):=t_x^*\mathcal L\otimes \mathcal L^{-1}$
, where
![]() $t_x\colon A\to A$
is translation by a point
$t_x\colon A\to A$
is translation by a point
![]() $x\in A$
. We denote by
$x\in A$
. We denote by
![]() $L_y\in \operatorname {\mathrm {Pic}}^0(A)$
the line bundle corresponding to a point
$L_y\in \operatorname {\mathrm {Pic}}^0(A)$
the line bundle corresponding to a point
![]() $y\in \hat {A}$
. Note that
$y\in \hat {A}$
. Note that
![]() $\phi _{\mathcal L}$
is dependent only on the Néron-Severi class of
$\phi _{\mathcal L}$
is dependent only on the Néron-Severi class of
![]() $\mathcal L$
, so we will use the notation
$\mathcal L$
, so we will use the notation
![]() $\phi _{[\mathcal L]}$
.
$\phi _{[\mathcal L]}$
.
Pullback by the translation map and tensoring by degree
![]() $0$
line bundles give automorphisms of
$0$
line bundles give automorphisms of
![]() $M_A(v)$
, and we are interested in when these automorphisms respect the Albanese morphism. That is, we identify in Theorem 3.1 below which of the
$M_A(v)$
, and we are interested in when these automorphisms respect the Albanese morphism. That is, we identify in Theorem 3.1 below which of the
![]() $L_y\otimes t_x^* \in \operatorname {\mathrm {Aut}} M_A(v)$
restrict to automorphisms of
$L_y\otimes t_x^* \in \operatorname {\mathrm {Aut}} M_A(v)$
restrict to automorphisms of
![]() $K_A(v)$
.
$K_A(v)$
.
Theorem 3.1. Let v be a Mukai vector as in Setting 2.4. There are exactly
![]() $n^4$
elements
$n^4$
elements
![]() $(x,y)\in A\times \hat {A}$
for which the automorphism
$(x,y)\in A\times \hat {A}$
for which the automorphism
![]() $L_y\otimes t_x^*$
on
$L_y\otimes t_x^*$
on
![]() $M_A(v)$
restricts to an automorphism on
$M_A(v)$
restricts to an automorphism on
![]() $K_A(v)$
. These elements form a subgroup
$K_A(v)$
. These elements form a subgroup
whose set of k-points is isomorphic to
![]() $({\mathbb Z}/n{\mathbb Z})^4$
.
$({\mathbb Z}/n{\mathbb Z})^4$
.
The elements of
![]() $G_A(v)$
are the solutions to the following equations on
$G_A(v)$
are the solutions to the following equations on
![]() $\hat {A}$
and A, where l and m are the Néron-Severi classes of L and M:
$\hat {A}$
and A, where l and m are the Néron-Severi classes of L and M:
Equivalently,
![]() $G_A(v)$
is the kernel of the following isogeny:
$G_A(v)$
is the kernel of the following isogeny:
 $$ \begin{align} \phi\colon A\times\hat{A} &\to A\times\hat{A} \\ (x,y)&\mapsto (\phi_m(y)-sx,\phi_l(x)+ry).\notag \end{align} $$
$$ \begin{align} \phi\colon A\times\hat{A} &\to A\times\hat{A} \\ (x,y)&\mapsto (\phi_m(y)-sx,\phi_l(x)+ry).\notag \end{align} $$
The proof of Theorem 3.1 requires analysis of
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
. We will crucially need the following lemma.
$\phi _m$
. We will crucially need the following lemma.
Lemma 3.2 (Yoshioka [Reference Yoshioka56, Lem. 4.2])
where
![]() $\chi :=\chi (L)=\chi (M)=\frac {l^2}{2}=n+rs$
.
$\chi :=\chi (L)=\chi (M)=\frac {l^2}{2}=n+rs$
.
Additionally, we recall that for any
![]() $\mathcal F\in D(A)$
,
$\mathcal F\in D(A)$
,
This follows from [Reference Mukai43, (3.1)]. Though the statement is not quite identical to the one we give here, it immediately follows from biduality of the Poincaré bundle [Reference Huybrechts26, 9.12].
Proof of Theorem 3.1
The main issue in this proof is that maps of the form
![]() $L_y\otimes t_x^*$
are not, in general, well-defined as automorphisms on
$L_y\otimes t_x^*$
are not, in general, well-defined as automorphisms on
![]() $K_A(v)$
. Given
$K_A(v)$
. Given
![]() $\mathcal F\in K_A(v)$
,
$\mathcal F\in K_A(v)$
,
![]() $L_y\otimes t_x^*\mathcal F$
has the same Mukai vector as
$L_y\otimes t_x^*\mathcal F$
has the same Mukai vector as
![]() $\mathcal F$
but may not have the same image under the Albanese morphism. For instance, pullback by
$\mathcal F$
but may not have the same image under the Albanese morphism. For instance, pullback by
![]() $t_x^*$
, in general, preserves Néron–Severi classes of line bundles and acts trivially on the structure sheaf, but it does not act trivially on all line bundles.
$t_x^*$
, in general, preserves Néron–Severi classes of line bundles and acts trivially on the structure sheaf, but it does not act trivially on all line bundles.
We therefore seek the
![]() $(x,y)\in A\times \hat {A}$
that satisfy the following conditions:
$(x,y)\in A\times \hat {A}$
that satisfy the following conditions:
 $$ \begin{align*} L&=\det(\mathcal F)=\det(L_y\otimes t_x^*\mathcal F)=L_y^{\otimes r}\otimes t_x^*\det(\mathcal F)= L_y^{\otimes r}\otimes t_x^*L\\ M&=\det(\Phi_P(\mathcal F))=\det(\Phi_P(L_y\otimes t_x^*(\mathcal F)))= \det(t_y^*(L_{-x}\otimes \Phi_P(\mathcal F)))\\ &\phantom{{}=\det(\Phi_P(\mathcal F))}= t_y^*(L_{-x}^{\otimes s}\otimes\det(\Phi_P(\mathcal F))) =t_y^*(L_{-x}^{\otimes s}\otimes M ) =L_{-x}^{\otimes s}\otimes t_y^* M. \end{align*} $$
$$ \begin{align*} L&=\det(\mathcal F)=\det(L_y\otimes t_x^*\mathcal F)=L_y^{\otimes r}\otimes t_x^*\det(\mathcal F)= L_y^{\otimes r}\otimes t_x^*L\\ M&=\det(\Phi_P(\mathcal F))=\det(\Phi_P(L_y\otimes t_x^*(\mathcal F)))= \det(t_y^*(L_{-x}\otimes \Phi_P(\mathcal F)))\\ &\phantom{{}=\det(\Phi_P(\mathcal F))}= t_y^*(L_{-x}^{\otimes s}\otimes\det(\Phi_P(\mathcal F))) =t_y^*(L_{-x}^{\otimes s}\otimes M ) =L_{-x}^{\otimes s}\otimes t_y^* M. \end{align*} $$
We may rewrite these conditions as the equations (3.1). Equivalently, these
![]() $(x,y)$
are the kernel of the map
$(x,y)$
are the kernel of the map
![]() $\phi $
in (3.2).
$\phi $
in (3.2).
Precomposing the map
![]() $\phi $
with
$\phi $
with
![]() $\psi \colon A\times \hat {A} \to A\times \hat {A}$
, where
$\psi \colon A\times \hat {A} \to A\times \hat {A}$
, where
![]() $\psi (x,y)= (\phi _m(y)-rx,\phi _l(x)+sy)$
, and applying Lemma 3.2, we have
$\psi (x,y)= (\phi _m(y)-rx,\phi _l(x)+sy)$
, and applying Lemma 3.2, we have
 $$ \begin{align*} \phi\circ\psi(x,y)&= \phi\circ(\phi_m(y)-rx,\phi_l(x)+sy)\\ &=(\phi_m(\phi_l(x)+sy)-s(\phi_m(y)-rx),\phi_l(\phi_m(y)-rx)+r(\phi_l(x)+sy))\\ &=(-\chi\cdot x+rsx,-\chi\cdot y+rsy)=-n(x,y). \end{align*} $$
$$ \begin{align*} \phi\circ\psi(x,y)&= \phi\circ(\phi_m(y)-rx,\phi_l(x)+sy)\\ &=(\phi_m(\phi_l(x)+sy)-s(\phi_m(y)-rx),\phi_l(\phi_m(y)-rx)+r(\phi_l(x)+sy))\\ &=(-\chi\cdot x+rsx,-\chi\cdot y+rsy)=-n(x,y). \end{align*} $$
Thus,
![]() $\phi \circ \psi =[-n]$
, so
$\phi \circ \psi =[-n]$
, so
![]() $\phi $
is surjective and is hence an isogeny. Similarly,
$\phi $
is surjective and is hence an isogeny. Similarly,
![]() $\psi \circ \phi =[-n]$
and
$\psi \circ \phi =[-n]$
and
![]() $G_A(v)\leqslant (A\times \hat {A})[n]$
.
$G_A(v)\leqslant (A\times \hat {A})[n]$
.
We show
![]() $G_A(v)\cong ({\mathbb Z}/n{\mathbb Z})^4$
in Lemma 3.6. This will require an understanding of preimages of elements under
$G_A(v)\cong ({\mathbb Z}/n{\mathbb Z})^4$
in Lemma 3.6. This will require an understanding of preimages of elements under
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
, which we study in Claims 3.4 and 3.5.
$\phi _m$
, which we study in Claims 3.4 and 3.5.
Remark 3.3. Since the maps
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
are determined by the Néron–Severi classes of L and M, the proof of Theorem 3.1 shows that the automorphisms of
$\phi _m$
are determined by the Néron–Severi classes of L and M, the proof of Theorem 3.1 shows that the automorphisms of
![]() $M_A(v)$
given by elements of
$M_A(v)$
given by elements of
![]() $G_A(v)$
will restrict to automorphisms of not just one, but any fiber of the Albanese morphism on
$G_A(v)$
will restrict to automorphisms of not just one, but any fiber of the Albanese morphism on
![]() $M_A(v)$
.
$M_A(v)$
.
Furthermore, for any
![]() $(x,y)\in (A\times \hat {A})[n]$
, the automorphism
$(x,y)\in (A\times \hat {A})[n]$
, the automorphism
![]() $L_y\otimes t_x^*$
induces a permutation of the Albanese fibers and if
$L_y\otimes t_x^*$
induces a permutation of the Albanese fibers and if
![]() $(x,y)\notin G_A(v)$
, this permutation does not have any fixed fibers.
$(x,y)\notin G_A(v)$
, this permutation does not have any fixed fibers.
If we extend the domain of
![]() $\det \times \det \Phi _P$
to elements of
$\det \times \det \Phi _P$
to elements of
![]() $D(A)$
with Mukai vector v (by mapping to the Grothendieck group before taking determinants),
$D(A)$
with Mukai vector v (by mapping to the Grothendieck group before taking determinants),
![]() $L_y\otimes t_x^*$
acts on the fibers of this map as well.
$L_y\otimes t_x^*$
acts on the fibers of this map as well.
Before proving Lemma 3.6, we need results on the kernels of
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
:
$\phi _m$
:
Claim 3.4. Let
![]() $p\neq \operatorname {\mathrm {char}} k$
be a prime and
$p\neq \operatorname {\mathrm {char}} k$
be a prime and
![]() $\chi \neq 0$
. Suppose
$\chi \neq 0$
. Suppose
![]() $p^q$
is the highest power of p dividing
$p^q$
is the highest power of p dividing
![]() $\chi $
. Then, the group of p-power torsion points in
$\chi $
. Then, the group of p-power torsion points in
![]() $\ker \phi _l\cong \ker \phi _m$
is
$\ker \phi _l\cong \ker \phi _m$
is
where
![]() $0\leq n_1\leq n_2$
and
$0\leq n_1\leq n_2$
and
![]() $n_1+n_2=q$
. If
$n_1+n_2=q$
. If
![]() $n_1>0$
, then L and M are
$n_1>0$
, then L and M are
![]() $p^{n_1}$
-st powers of other line bundles.
$p^{n_1}$
-st powers of other line bundles.
If L and M are separable, we may define their polarization type to be the termwise product of pairs
![]() $(p^{n_1},p^{n_2})$
as p varies over primes dividing
$(p^{n_1},p^{n_2})$
as p varies over primes dividing
![]() $\chi $
(cf. [Reference Birkenhake and Lange6, §2]).
$\chi $
(cf. [Reference Birkenhake and Lange6, §2]).
Proof. Since
![]() $\ker \phi _l \cong \ker \phi _{-l}$
and
$\ker \phi _l \cong \ker \phi _{-l}$
and
![]() $\chi (L) \neq 0$
, we may assume that L is ample. The proof of Riemann–Roch for abelian varieties in [Reference Naruki47, §16] implies that the degree of
$\chi (L) \neq 0$
, we may assume that L is ample. The proof of Riemann–Roch for abelian varieties in [Reference Naruki47, §16] implies that the degree of
![]() $\phi _l$
is
$\phi _l$
is
![]() $\chi ^2$
. The structure of
$\chi ^2$
. The structure of
![]() $\ker \phi _l \cap A[p^q]$
is then determined by Lemma 3.2 and the fact that the Weil pairing
$\ker \phi _l \cap A[p^q]$
is then determined by Lemma 3.2 and the fact that the Weil pairing
![]() $e^L$
on the p-torsion is skew-symmetric [Reference Naruki47, §20, Thm. 1]. Since
$e^L$
on the p-torsion is skew-symmetric [Reference Naruki47, §20, Thm. 1]. Since
![]() $\phi _m$
is the negative of the dual of
$\phi _m$
is the negative of the dual of
![]() $\phi _l$
[Reference Birkenhake and Lange6, §2], the group structure of p-power torsion points in
$\phi _l$
[Reference Birkenhake and Lange6, §2], the group structure of p-power torsion points in
![]() $\ker \phi _m$
is isomorphic to that in
$\ker \phi _m$
is isomorphic to that in
![]() $\ker \phi _l$
. The last statement is a consequence of [Reference Naruki47, §23, Thm. 3].
$\ker \phi _l$
. The last statement is a consequence of [Reference Naruki47, §23, Thm. 3].
The images of any two elements of the same order under the compositions
![]() $\phi _l\circ \phi _m$
or
$\phi _l\circ \phi _m$
or
![]() $\phi _m\circ \phi _l$
will have the same order. However,
$\phi _m\circ \phi _l$
will have the same order. However,
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
do not respect orders in this way.
$\phi _m$
do not respect orders in this way.
Claim 3.5. Let
![]() $p\neq \operatorname {\mathrm {char}} k$
be a prime dividing
$p\neq \operatorname {\mathrm {char}} k$
be a prime dividing
![]() $\chi $
, and assume that l and m are not p-th multiples of other classes, so
$\chi $
, and assume that l and m are not p-th multiples of other classes, so
![]() $n_1=0$
. Suppose
$n_1=0$
. Suppose
![]() $p^d\mid \chi $
for some
$p^d\mid \chi $
for some
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
-
(a) Suppose
 $u\in A[p^d]\cap \ker {\phi _l}$
. Then, the preimage of u in
$u\in A[p^d]\cap \ker {\phi _l}$
. Then, the preimage of u in
 $\hat {A}[p^d]$
under
$\hat {A}[p^d]$
under
 $\phi _m$
is of the form
$\phi _m$
is of the form
 $b+({\mathbb Z}/p^d{\mathbb Z})^2$
for some
$b+({\mathbb Z}/p^d{\mathbb Z})^2$
for some
 $b\in \hat {A}[p^d]$
.
$b\in \hat {A}[p^d]$
. -
(b) Suppose
 $v\in \hat {A}[p^d]\cap \ker {\phi _m}$
. Then, the preimage of v in
$v\in \hat {A}[p^d]\cap \ker {\phi _m}$
. Then, the preimage of v in
 $\hat {A}[p^d]$
vnder
$\hat {A}[p^d]$
vnder
 $\phi _l$
is of the form
$\phi _l$
is of the form
 $a+({\mathbb Z}/p^d{\mathbb Z})^2$
for some
$a+({\mathbb Z}/p^d{\mathbb Z})^2$
for some
 $a\in {A}[p^d]$
.
$a\in {A}[p^d]$
.
Now, suppose
![]() $p^q=\chi $
.
$p^q=\chi $
.
-
(c) Suppose
 $u\in A$
and
$u\in A$
and
 $\phi _l(u)$
has order
$\phi _l(u)$
has order
 $p^c$
. Then, the preimage of u in
$p^c$
. Then, the preimage of u in
 $\hat {A}$
under
$\hat {A}$
under
 $\phi _m$
is of the form
$\phi _m$
is of the form
 $b+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
$b+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
 $b\in \hat {A}[p^{c+q}]$
.
$b\in \hat {A}[p^{c+q}]$
. -
(d) Suppose
 $v\in \hat {A}$
and
$v\in \hat {A}$
and
 $\phi _m(v)$
has order
$\phi _m(v)$
has order
 $p^c$
. Then, the preimage of v in
$p^c$
. Then, the preimage of v in
 ${A}$
under
${A}$
under
 $\phi _l$
is of the form
$\phi _l$
is of the form
 $a+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
$a+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
 $b\in \hat {A}[p^{c+q}]$
.
$b\in \hat {A}[p^{c+q}]$
.
Proof. (a) By Lemma 3.2, the composition
![]() $\phi _l\circ \phi _m$
is given by multiplication by
$\phi _l\circ \phi _m$
is given by multiplication by
![]() $-\chi $
. Thus,
$-\chi $
. Thus,
![]() $\phi _m\circ \phi _l$
acts on
$\phi _m\circ \phi _l$
acts on
![]() $A[p^d]$
as the zero map, and hence,
$A[p^d]$
as the zero map, and hence,
By Claim 3.4,
![]() $A[p^d]\cap \ker \phi _l$
has
$A[p^d]\cap \ker \phi _l$
has
![]() $p^{2d}$
elements and
$p^{2d}$
elements and
![]() $\phi _m$
acting on
$\phi _m$
acting on
![]() $\hat {A}[p^d]$
is a
$\hat {A}[p^d]$
is a
![]() $p^{2d}$
-to-
$p^{2d}$
-to-
![]() $1$
map. It follows by counting that
$1$
map. It follows by counting that
![]() $\operatorname {\mathrm {im}} \phi _m|_{\hat {A}[p^d]} = A[p^d]\cap \ker \phi _l$
. By Claim 3.4, the preimage of u is as stated.
$\operatorname {\mathrm {im}} \phi _m|_{\hat {A}[p^d]} = A[p^d]\cap \ker \phi _l$
. By Claim 3.4, the preimage of u is as stated.
Part (b) follows analogously.
(c) By Lemma 3.2, the preimage of
![]() $\phi _l(u)$
under
$\phi _l(u)$
under
![]() $\phi _l\circ \phi _m$
consists of elements of order
$\phi _l\circ \phi _m$
consists of elements of order
![]() $p^{c+q}$
. By Lemma 3.4, the result follows.
$p^{c+q}$
. By Lemma 3.4, the result follows.
Part (d) follows analogously.
The following result is proved using a case-by-case argument. The explicit argument given has the advantage of aiding in the analysis of examples. See [Reference Matsushita38, Lemma 10.1] for an approach using deformations over
![]() ${\mathbb C}$
.
${\mathbb C}$
.
Lemma 3.6. The solutions to the equations (3.1) form a group isomorphic to
![]() $({\mathbb Z}/n{\mathbb Z})^4 \leqslant (A\times \hat {A})[n]$
.
$({\mathbb Z}/n{\mathbb Z})^4 \leqslant (A\times \hat {A})[n]$
.
Proof.
Case 1:
![]() $\chi =0$
.
$\chi =0$
.
Both L and M must have degree
![]() $0$
, so
$0$
, so
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _m$
are both the
$\phi _m$
are both the
![]() $0$
-morphism. The equations (3.1) simplify to
$0$
-morphism. The equations (3.1) simplify to
Furthermore,
![]() $n=-rs$
. Since
$n=-rs$
. Since
![]() $v=(r,l,s)$
is positive and
$v=(r,l,s)$
is positive and
![]() $v^2\geq 4$
, we must have
$v^2\geq 4$
, we must have
![]() $r>0$
and
$r>0$
and
![]() $s<0$
. The solutions consist of all products of
$s<0$
. The solutions consist of all products of
![]() $|s|$
-torsion points on A and r-torsion points on
$|s|$
-torsion points on A and r-torsion points on
![]() $\hat {A}$
.
$\hat {A}$
.
The group of solutions is isomorphic to
![]() $({\mathbb Z}/r{\mathbb Z})^4 \times ({\mathbb Z}/|s|{\mathbb Z})^4$
, hence
$({\mathbb Z}/r{\mathbb Z})^4 \times ({\mathbb Z}/|s|{\mathbb Z})^4$
, hence
![]() $({\mathbb Z}/n{\mathbb Z})^4$
, since in this case, primitivity of the Mukai vector implies r and s are relatively prime.
$({\mathbb Z}/n{\mathbb Z})^4$
, since in this case, primitivity of the Mukai vector implies r and s are relatively prime.
Now, let p be a prime divisor of n and
![]() $p^q$
be the highest power of p dividing n. We treat the remaining cases by analyzing solutions in
$p^q$
be the highest power of p dividing n. We treat the remaining cases by analyzing solutions in
![]() $(A\times \hat {A})[p^q]$
. We may then conclude by using the Sun Zi Remainder Theorem.
$(A\times \hat {A})[p^q]$
. We may then conclude by using the Sun Zi Remainder Theorem.
Case 2:
![]() $\chi \neq 0$
and at least one of r or s is relatively prime with p.
$\chi \neq 0$
and at least one of r or s is relatively prime with p.
Suppose r is relatively prime with p. Fix an arbitrary
![]() $x\in A[p^q]$
. The equation
$x\in A[p^q]$
. The equation
![]() $\phi _l(x)=-ry$
then has exactly one solution y because multiplication by
$\phi _l(x)=-ry$
then has exactly one solution y because multiplication by
![]() $-r$
acts bijectively on
$-r$
acts bijectively on
![]() $\hat {A}[p^q]$
.
$\hat {A}[p^q]$
.
Now we check that
![]() $(x,y)$
is a solution to (3.1): Applying
$(x,y)$
is a solution to (3.1): Applying
![]() $\phi _m$
, we have
$\phi _m$
, we have
![]() $\phi _m\circ \phi _l(x)=-r\phi _m(y)$
. Using Lemma 3.2, we then have
$\phi _m\circ \phi _l(x)=-r\phi _m(y)$
. Using Lemma 3.2, we then have
![]() $-rsx=-r\phi _m(y)$
. Since x and y are
$-rsx=-r\phi _m(y)$
. Since x and y are
![]() $p^q$
-torsion, multiplication by
$p^q$
-torsion, multiplication by
![]() $-r$
acts bijectively, implying
$-r$
acts bijectively, implying
![]() $sx=\phi _m(y)$
.
$sx=\phi _m(y)$
.
Thus, for each
![]() $x\in A[p^q]$
, there is one
$x\in A[p^q]$
, there is one
![]() $y\in \hat {A}[p^q]$
so that
$y\in \hat {A}[p^q]$
so that
![]() $(x,y)$
is a solution to (3.1). The projection map
$(x,y)$
is a solution to (3.1). The projection map
![]() $(x,y)\mapsto x$
gives an isomorphism from solutions to (3.1) to
$(x,y)\mapsto x$
gives an isomorphism from solutions to (3.1) to
![]() $A[p^q]\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
$A[p^q]\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
If s is relatively prime with p, an analogous argument shows there is exactly one solution
![]() $(x,y)$
to (3.1) for each
$(x,y)$
to (3.1) for each
![]() $y\in \hat {A}[p^q]$
and that, again, the group of all solutions is isomorphic to
$y\in \hat {A}[p^q]$
and that, again, the group of all solutions is isomorphic to
![]() $({\mathbb Z}/p^q{\mathbb Z})^4$
.
$({\mathbb Z}/p^q{\mathbb Z})^4$
.
Cases 1 and 2 have covered all cases where r and s are not both divisible by p. Going forward, we assume
![]() $p\mid r$
and
$p\mid r$
and
![]() $p\mid s$
. If
$p\mid s$
. If
![]() $\operatorname {\mathrm {char}}(k)\neq 0$
, our assumption in Setting 2.4 that
$\operatorname {\mathrm {char}}(k)\neq 0$
, our assumption in Setting 2.4 that
![]() $\operatorname {\mathrm {char}}(k)\nmid n$
implies in the following cases that
$\operatorname {\mathrm {char}}(k)\nmid n$
implies in the following cases that
![]() $\operatorname {\mathrm {char}}(k)\neq p$
, and so we may apply Claim 3.4. By the primitivity of the Mukai vector,
$\operatorname {\mathrm {char}}(k)\neq p$
, and so we may apply Claim 3.4. By the primitivity of the Mukai vector,
![]() $n_1=0$
and
$n_1=0$
and
![]() $n_2$
is equal to the highest power of p dividing
$n_2$
is equal to the highest power of p dividing
![]() $\chi $
.
$\chi $
.
Let j be the highest power of p dividing r and k be the highest power of p dividing s. If r or s is
![]() $0$
, we choose the convention that j or k is
$0$
, we choose the convention that j or k is
![]() $\infty $
.
$\infty $
.
In each of Cases 3, 4, 5, we handle in stages the situations where q becomes higher and higher relative to j and k. From now on, we assume
![]() $j\geq k$
. If
$j\geq k$
. If
![]() $k>j$
, the argument is analogous.
$k>j$
, the argument is analogous.
Case 3:
![]() $\chi \neq 0$
,
$\chi \neq 0$
,
![]() $0<k\leq j$
and
$0<k\leq j$
and
![]() $q\leq j$
. We observe that
$q\leq j$
. We observe that
![]() $p^q$
is the highest power of p that divides
$p^q$
is the highest power of p that divides
![]() $\chi $
.
$\chi $
.
Solutions
![]() $(x,y)\in (A\times \hat {A})[p^q]$
to the first equation in (3.1) are precisely those where
$(x,y)\in (A\times \hat {A})[p^q]$
to the first equation in (3.1) are precisely those where
![]() $\phi _l(x)=0$
. By Claim 3.4, the group of such x is isomorphic to
$\phi _l(x)=0$
. By Claim 3.4, the group of such x is isomorphic to
![]() $({\mathbb Z}/p^q{\mathbb Z})^2$
.
$({\mathbb Z}/p^q{\mathbb Z})^2$
.
Fix such an x. We observe that
![]() $sx\in A[p^q]$
and
$sx\in A[p^q]$
and
![]() $\phi _l(sx)=0$
. By Claim 3.5(a), the preimage of
$\phi _l(sx)=0$
. By Claim 3.5(a), the preimage of
![]() $sx$
under
$sx$
under
![]() $\phi _m$
in
$\phi _m$
in
![]() $\hat {A}[p^q]$
is of the form
$\hat {A}[p^q]$
is of the form
![]() $b+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
$b+({\mathbb Z}/p^q{\mathbb Z})^2$
for some
![]() $b\in \hat {A}[p^q]$
. Thus, there are
$b\in \hat {A}[p^q]$
. Thus, there are
![]() $p^{4q}$
total solutions.
$p^{4q}$
total solutions.
The projection
![]() $(x,y)\mapsto x$
gives a surjective group homomorphism
$(x,y)\mapsto x$
gives a surjective group homomorphism
![]() $G_A(v)\twoheadrightarrow ({\mathbb Z}/p^q{\mathbb Z})^2$
. The kernel of this map consists of all solutions where
$G_A(v)\twoheadrightarrow ({\mathbb Z}/p^q{\mathbb Z})^2$
. The kernel of this map consists of all solutions where
![]() $x=0$
, which by Claim 3.4 is isomorphic to
$x=0$
, which by Claim 3.4 is isomorphic to
![]() $({\mathbb Z}/p^q{\mathbb Z})^2$
. Since
$({\mathbb Z}/p^q{\mathbb Z})^2$
. Since
![]() $G_A(v)\leqslant (A\times \hat {A})[p^q]\cong ({\mathbb Z}/p^q{\mathbb Z})^8$
, this short exact sequence shows it must be isomorphic to
$G_A(v)\leqslant (A\times \hat {A})[p^q]\cong ({\mathbb Z}/p^q{\mathbb Z})^8$
, this short exact sequence shows it must be isomorphic to
![]() $({\mathbb Z}/p^q{\mathbb Z})^4$
.
$({\mathbb Z}/p^q{\mathbb Z})^4$
.
In Cases 4 and 5, we make a reduction argument. We observe that for any
![]() $(x,y)\in G_A(v)$
,
$(x,y)\in G_A(v)$
,
![]() $(sx,sy)\in G_A(v)\cap (A\times \hat {A})[p^{q-k}]$
. In each of Cases 4 and 5, we will show that the map
$(sx,sy)\in G_A(v)\cap (A\times \hat {A})[p^{q-k}]$
. In each of Cases 4 and 5, we will show that the map
given by multiplication by s is surjective and
![]() $p^{4k}$
-to-
$p^{4k}$
-to-
![]() $1$
. This argument may be repeated to reduce each case to previous cases.
$1$
. This argument may be repeated to reduce each case to previous cases.
Case 4:
![]() $\chi \neq 0$
,
$\chi \neq 0$
,
![]() $0<k \leq j< q$
and
$0<k \leq j< q$
and
![]() $q\leq j+k$
.
$q\leq j+k$
.
We note that
![]() $p^q\mid \chi $
. Since
$p^q\mid \chi $
. Since
![]() $q-k\leq j$
, the argument in Case 3 shows that
$q-k\leq j$
, the argument in Case 3 shows that
Let
![]() $(u,v)\in G_A(v)\cap (A\times \hat {A})[p^{q-k}]$
. We seek
$(u,v)\in G_A(v)\cap (A\times \hat {A})[p^{q-k}]$
. We seek
![]() $(x,y)\in G_A(v)< (A\times \hat {A})[p^{q}]$
, where
$(x,y)\in G_A(v)< (A\times \hat {A})[p^{q}]$
, where
![]() $(sx,sy)=(u,v)$
. First, we search for elements y, where
$(sx,sy)=(u,v)$
. First, we search for elements y, where
![]() $\phi _m(y)=u$
and
$\phi _m(y)=u$
and
![]() $sy=v$
. Thus, we look at the preimage of u under
$sy=v$
. Thus, we look at the preimage of u under
![]() $\phi _m$
and analyze which of those elements give v when multiplied by s.
$\phi _m$
and analyze which of those elements give v when multiplied by s.
Note that
![]() $\phi _l(u)=-rv=0$
. Since u is
$\phi _l(u)=-rv=0$
. Since u is
![]() $p^{q-k}$
-torsion, it is also
$p^{q-k}$
-torsion, it is also
![]() $p^q$
-torsion. So by Claim 3.5(a), the preimage of u under
$p^q$
-torsion. So by Claim 3.5(a), the preimage of u under
![]() $\phi _m$
in
$\phi _m$
in
![]() $\hat {A}[p^q]$
is of the form
$\hat {A}[p^q]$
is of the form
![]() $b+({\mathbb Z}/p^q{\mathbb Z})^2$
, where
$b+({\mathbb Z}/p^q{\mathbb Z})^2$
, where
![]() $b\in \hat {A}[p^{q}]$
. Multiplying by s gives a
$b\in \hat {A}[p^{q}]$
. Multiplying by s gives a
![]() $p^{2k}$
-to-
$p^{2k}$
-to-
![]() $1$
map on the following cosets:
$1$
map on the following cosets:
We will now show that v is in the image of this map: the preimage of
![]() $su$
under
$su$
under
![]() $\phi _m$
in
$\phi _m$
in
![]() $\hat {A}[p^q]$
is of the form
$\hat {A}[p^q]$
is of the form
![]() $v+({\mathbb Z}/p^q{\mathbb Z})^2$
. The preimage of
$v+({\mathbb Z}/p^q{\mathbb Z})^2$
. The preimage of
![]() $su$
under
$su$
under
![]() $\phi _m$
that is
$\phi _m$
that is
![]() $p^{q-k}$
-torsion is thus of the form
$p^{q-k}$
-torsion is thus of the form
![]() $v+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
and has exactly
$v+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
and has exactly
![]() $p^{2(q-k)}$
elements. Now, the elements of
$p^{2(q-k)}$
elements. Now, the elements of
![]() $sb+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
are
$sb+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
are
![]() $p^{q-k}$
-torsion, there are
$p^{q-k}$
-torsion, there are
![]() $p^{2(q-k)}$
of them and their image under
$p^{2(q-k)}$
of them and their image under
![]() $\phi _m$
is
$\phi _m$
is
![]() $su$
. Thus, these sets are equal, implying
$su$
. Thus, these sets are equal, implying
![]() $v\in sb+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. Thus, there are
$v\in sb+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. Thus, there are
![]() $p^{2k}$
elements
$p^{2k}$
elements
![]() $y\in \hat {A}[p^q]$
with the desired properties.
$y\in \hat {A}[p^q]$
with the desired properties.
Now we search for elements x, where
![]() $\phi _l(x)=-ry=-\frac {r}{s}v$
and
$\phi _l(x)=-ry=-\frac {r}{s}v$
and
![]() $sx=u$
. Note that since
$sx=u$
. Note that since
![]() $j\geq k$
,
$j\geq k$
,
![]() $-\frac {r}{s}=\frac {cp^e}{d}$
for some c, d relatively prime with p. We may define multiplying by
$-\frac {r}{s}=\frac {cp^e}{d}$
for some c, d relatively prime with p. We may define multiplying by
![]() $\frac {1}{d}$
on p-power torsion points by taking the preimage under multiplication by d since it is a bijection on such points. We examine the preimage of
$\frac {1}{d}$
on p-power torsion points by taking the preimage under multiplication by d since it is a bijection on such points. We examine the preimage of
![]() $-\frac {r}{s}v$
under
$-\frac {r}{s}v$
under
![]() $\phi _l$
and analyze which of those elements give u when multiplied by s.
$\phi _l$
and analyze which of those elements give u when multiplied by s.
Note
![]() $\phi _m(-\frac {r}{s}v)=-ru=0$
. So by Claim 3.5(b), the preimage of
$\phi _m(-\frac {r}{s}v)=-ru=0$
. So by Claim 3.5(b), the preimage of
![]() $-\frac {r}{s}v$
under
$-\frac {r}{s}v$
under
![]() $\phi _l$
is of the form
$\phi _l$
is of the form
![]() $a+({\mathbb Z}/p^q{\mathbb Z})^2$
, where
$a+({\mathbb Z}/p^q{\mathbb Z})^2$
, where
![]() $a\in {A}[p^{q}]$
.
$a\in {A}[p^{q}]$
.
Multiplying by s gives a
![]() $p^{2k}$
-to-
$p^{2k}$
-to-
![]() $1$
map on the following cosets:
$1$
map on the following cosets:
We will now show that u is in the image of this map: The preimage of
![]() $-rv$
under
$-rv$
under
![]() $\phi _l$
in
$\phi _l$
in
![]() $A[p^q]$
is of the form
$A[p^q]$
is of the form
![]() $u+({\mathbb Z}/p^q{\mathbb Z})^2$
. The preimage of
$u+({\mathbb Z}/p^q{\mathbb Z})^2$
. The preimage of
![]() $-rv$
under
$-rv$
under
![]() $\phi _l$
that is
$\phi _l$
that is
![]() $p^{q-k}$
-torsion is thus of the form
$p^{q-k}$
-torsion is thus of the form
![]() $u+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. The elements of
$u+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. The elements of
![]() $sa+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
are
$sa+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
are
![]() $p^{q-k}$
-torsion and their image under
$p^{q-k}$
-torsion and their image under
![]() $\phi _l$
is
$\phi _l$
is
![]() $-rv$
. Thus, these sets are equal, implying
$-rv$
. Thus, these sets are equal, implying
![]() $u\in sa+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. In summary, there are
$u\in sa+({\mathbb Z}/p^{q-k}{\mathbb Z})^2$
. In summary, there are
![]() $p^{2k}$
elements
$p^{2k}$
elements
![]() $x\in A[p^q]$
, where
$x\in A[p^q]$
, where
![]() $\phi _l(x)=-\frac {r}{s}v=-ry$
and
$\phi _l(x)=-\frac {r}{s}v=-ry$
and
![]() $sx=u$
.
$sx=u$
.
This shows that (3.3) is a surjective
![]() $p^{4k}$
-to-
$p^{4k}$
-to-
![]() $1$
map. Since multiplication by s decreases the order of the p-power torsion of an element by exactly
$1$
map. Since multiplication by s decreases the order of the p-power torsion of an element by exactly
![]() $p^k$
, by (3.4) we may conclude that
$p^k$
, by (3.4) we may conclude that
![]() $G_A(v)\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
$G_A(v)\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
Case 5:
![]() $\chi \neq 0$
,
$\chi \neq 0$
,
![]() $0<k\leq j< q$
and
$0<k\leq j< q$
and
![]() $j+k<q$
. In this case,
$j+k<q$
. In this case,
![]() $p^{j+k}$
divides
$p^{j+k}$
divides
![]() $\chi $
and no higher powers of p may divide
$\chi $
and no higher powers of p may divide
![]() $\chi $
.
$\chi $
.
By the argument in Case 4, we have
We will first extend our result for solutions of order up to
![]() $p^{j+2k}$
. For convenience, define
$p^{j+2k}$
. For convenience, define
![]() $t:=\min \{q,j+2k\}$
.
$t:=\min \{q,j+2k\}$
.
Let
We seek
so that
![]() $(sx,sy)=(u,v)$
. First, we search for elements y, where
$(sx,sy)=(u,v)$
. First, we search for elements y, where
![]() $\phi _m(y)=u$
and
$\phi _m(y)=u$
and
![]() $sy=v$
; thus, we look at the preimage of u under
$sy=v$
; thus, we look at the preimage of u under
![]() $\phi _m$
and analyze which of those elements give v when multiplied by s.
$\phi _m$
and analyze which of those elements give v when multiplied by s.
If
![]() $\phi _l(u)=0$
, then the argument from Case 4 shows that there are
$\phi _l(u)=0$
, then the argument from Case 4 shows that there are
![]() $p^{2k}$
elements
$p^{2k}$
elements
![]() $y\in \hat {A}[p^{t}]$
, where
$y\in \hat {A}[p^{t}]$
, where
![]() $\phi _m(y)=u$
and
$\phi _m(y)=u$
and
![]() $sy=v$
.
$sy=v$
.
If
![]() $\phi _l(u)\in \hat {A}[p^k]\setminus \{0\}$
, then by Claim 3.5(c), the preimage of u under
$\phi _l(u)\in \hat {A}[p^k]\setminus \{0\}$
, then by Claim 3.5(c), the preimage of u under
![]() $\phi _m$
in
$\phi _m$
in
![]() $\hat {A}[p^{t}]$
is of the form
$\hat {A}[p^{t}]$
is of the form
![]() $b+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
$b+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
![]() $b\in \hat {A}[p^{t}]\setminus \hat {A}[p^{j+k}]$
.
$b\in \hat {A}[p^{t}]\setminus \hat {A}[p^{j+k}]$
.
Note that
![]() $\phi _l(\phi _m(b))=-rv$
and by Lemma 3.2,
$\phi _l(\phi _m(b))=-rv$
and by Lemma 3.2,
![]() $-rsb=-(n+rs)b=-rv$
. Multiplication by s gives a
$-rsb=-(n+rs)b=-rv$
. Multiplication by s gives a
![]() $p^{2k}$
-to-
$p^{2k}$
-to-
![]() $1$
map on the following cosets:
$1$
map on the following cosets:
We will now show that v is in the image of this map.
The preimage of
![]() $su$
under
$su$
under
![]() $\phi _m$
in
$\phi _m$
in
![]() $\hat {A}[p^{j+k}]$
is of the form
$\hat {A}[p^{j+k}]$
is of the form
![]() $v+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
. The part of
$v+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
. The part of
![]() $v+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
whose image under multiplication by
$v+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
whose image under multiplication by
![]() $-r$
is
$-r$
is
![]() $-rv$
is of the form
$-rv$
is of the form
![]() $v+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Since
$v+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Since
![]() $\phi _m$
maps
$\phi _m$
maps
![]() $sb+({\mathbb Z}/p^{j}{\mathbb Z})^2$
to
$sb+({\mathbb Z}/p^{j}{\mathbb Z})^2$
to
![]() $su$
and multiplying this coset by
$su$
and multiplying this coset by
![]() $-r$
gives
$-r$
gives
![]() $-rv$
, by counting elements,
$-rv$
, by counting elements,
![]() $sb+({\mathbb Z}/p^{j}{\mathbb Z})^2=v+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Hence,
$sb+({\mathbb Z}/p^{j}{\mathbb Z})^2=v+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Hence,
![]() $v\in sb+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Thus, there are
$v\in sb+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Thus, there are
![]() $p^{2k}$
elements
$p^{2k}$
elements
![]() $y\in b+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
$y\in b+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
![]() $\phi _m(y)=u$
and
$\phi _m(y)=u$
and
![]() $sy=v$
.
$sy=v$
.
Now we search for elements x where
![]() $\phi _l(x)=-ry=-\frac {r}{s}v$
and
$\phi _l(x)=-ry=-\frac {r}{s}v$
and
![]() $sx=u$
. We examine the preimage of
$sx=u$
. We examine the preimage of
![]() $-\frac {r}{s}v$
under
$-\frac {r}{s}v$
under
![]() $\phi _l$
and analyze which of those elements give u when multiplied by s.
$\phi _l$
and analyze which of those elements give u when multiplied by s.
If
![]() $\phi _m(-\frac {r}{s}v)=-ru=0$
, we may conclude using the arguments in Case 4. Otherwise, by Claim 3.5(d), the preimage of
$\phi _m(-\frac {r}{s}v)=-ru=0$
, we may conclude using the arguments in Case 4. Otherwise, by Claim 3.5(d), the preimage of
![]() $-\frac {r}{s}v$
under
$-\frac {r}{s}v$
under
![]() $\phi _l$
in
$\phi _l$
in
![]() $A[p^{t}]$
is of the form
$A[p^{t}]$
is of the form
![]() $a+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
where
$a+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
where
![]() $a\in {A}[p^{t}]\setminus {A}[p^{j+k}]$
. Note that
$a\in {A}[p^{t}]\setminus {A}[p^{j+k}]$
. Note that
![]() $\phi _m(\phi _l(a))=-ru$
and by Lemma 3.2,
$\phi _m(\phi _l(a))=-ru$
and by Lemma 3.2,
![]() $-rsa=-ru$
.
$-rsa=-ru$
.
Multiplying by s gives a
![]() $p^{2k}$
-to-
$p^{2k}$
-to-
![]() $1$
map on cosets:
$1$
map on cosets:
We will now show that u is in the image of this map. The preimage of
![]() $-rv$
under
$-rv$
under
![]() $\phi _l$
is of the form
$\phi _l$
is of the form
![]() $u+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
. The part of
$u+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
. The part of
![]() $u+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
whose image under multiplication by
$u+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
whose image under multiplication by
![]() $-r$
is
$-r$
is
![]() $-ru$
is of the form
$-ru$
is of the form
![]() $u+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. We have shown that
$u+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. We have shown that
![]() $\phi _l$
maps
$\phi _l$
maps
![]() $sa+({\mathbb Z}/p^{j}{\mathbb Z})^2$
to
$sa+({\mathbb Z}/p^{j}{\mathbb Z})^2$
to
![]() $-rv$
and multiplying this coset by
$-rv$
and multiplying this coset by
![]() $-r$
gives
$-r$
gives
![]() $-ru$
. By counting elements, we have the set equality
$-ru$
. By counting elements, we have the set equality
![]() $sa+({\mathbb Z}/p^{j}{\mathbb Z})^2=u+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Hence,
$sa+({\mathbb Z}/p^{j}{\mathbb Z})^2=u+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Hence,
![]() $u\in sa+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Thus, there are
$u\in sa+({\mathbb Z}/p^{j}{\mathbb Z})^2$
. Thus, there are
![]() $p^{2k}$
elements
$p^{2k}$
elements
![]() $x\in a+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
$x\in a+({\mathbb Z}/p^{j+k}{\mathbb Z})^2$
, where
![]() $\phi _l(x)=-\frac {r}{s}v$
and
$\phi _l(x)=-\frac {r}{s}v$
and
![]() $sx=u$
. Thus, the following map is surjective and
$sx=u$
. Thus, the following map is surjective and
![]() $p^{4k}$
-to-
$p^{4k}$
-to-
![]() $1$
:
$1$
:
If
![]() $q\leq j+2k$
, we may now conclude, in combination with (3.5), that
$q\leq j+2k$
, we may now conclude, in combination with (3.5), that
![]() $G_A(v)\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
$G_A(v)\cong ({\mathbb Z}/p^q{\mathbb Z})^4$
.
If
![]() $q> j+2k$
, (3.6) shows that
$q> j+2k$
, (3.6) shows that
![]() $G_A(v)\cap (A\times \hat {A})[p^{j+2k}]\cong ({\mathbb Z}/p^{j+2k}{\mathbb Z})^4$
. The above argument may be repeated for solutions of orders up to
$G_A(v)\cap (A\times \hat {A})[p^{j+2k}]\cong ({\mathbb Z}/p^{j+2k}{\mathbb Z})^4$
. The above argument may be repeated for solutions of orders up to
![]() $p^{j+3k}$
and then upward inductively to conclude that
$p^{j+3k}$
and then upward inductively to conclude that
![]() $G_A(v)\cong ({\mathbb Z}/p^{q}{\mathbb Z})^4$
.
$G_A(v)\cong ({\mathbb Z}/p^{q}{\mathbb Z})^4$
.
Example 3.7. (a) For
![]() $K_2(A)\cong K_A(1,0,-3)$
, l and m are the trivial Néron-Severi classes (these are treated in general by Case 1 of the proof of Lemma 3.6), so
$K_2(A)\cong K_A(1,0,-3)$
, l and m are the trivial Néron-Severi classes (these are treated in general by Case 1 of the proof of Lemma 3.6), so
![]() $\phi _l(x)=0$
and
$\phi _l(x)=0$
and
![]() $\phi _m(y)=0$
. The equations (3.1) simplify to
$\phi _m(y)=0$
. The equations (3.1) simplify to
![]() $0=-y$
and
$0=-y$
and
![]() $0=-3x$
, which recovers the fact that the group of symplectic automorphisms for
$0=-3x$
, which recovers the fact that the group of symplectic automorphisms for
![]() $K_2(A)$
is generated by
$K_2(A)$
is generated by
![]() $\iota $
and translation by elements of
$\iota $
and translation by elements of
![]() $A[3]$
[Reference Bolognesi and Massarenti8, Cor. 5(2)].
$A[3]$
[Reference Bolognesi and Massarenti8, Cor. 5(2)].
(b) In Sections 6–8, we consider fourfolds
![]() $K_A(v)$
, where
$K_A(v)$
, where
![]() $v=(0,l,s)$
for l primitive and
$v=(0,l,s)$
for l primitive and
![]() $\chi =3$
. If
$\chi =3$
. If
![]() $s\equiv s'\ \textrm {mod}\ 3$
, then
$s\equiv s'\ \textrm {mod}\ 3$
, then
![]() $G_A(0,l,s)=G_A(0,l,s')$
, leaving only three possible distinct groups of this form, which are described by a combination of Cases 2 and 3 of Lemma 3.6. Case 2 shows that
$G_A(0,l,s)=G_A(0,l,s')$
, leaving only three possible distinct groups of this form, which are described by a combination of Cases 2 and 3 of Lemma 3.6. Case 2 shows that
![]() $G_A(0,l,1)$
and
$G_A(0,l,1)$
and
![]() $G_A(0,l,2)$
, though in general distinct, each have one element
$G_A(0,l,2)$
, though in general distinct, each have one element
![]() $(x,y)\in (A\times \hat {A})[3]$
for every
$(x,y)\in (A\times \hat {A})[3]$
for every
![]() $y\in \hat {A}[3]$
: for any
$y\in \hat {A}[3]$
: for any
![]() $y\in \hat {A}[3]$
, there is one
$y\in \hat {A}[3]$
, there is one
![]() $x\in \ker \phi _l$
so that
$x\in \ker \phi _l$
so that
![]() $t_y^*M\simeq L_{x}\otimes M$
. However, we see from Case 3 that
$t_y^*M\simeq L_{x}\otimes M$
. However, we see from Case 3 that
![]() $G_A(0,l,0)$
is the product of
$G_A(0,l,0)$
is the product of
![]() $\ker \phi _l$
and
$\ker \phi _l$
and
![]() $\ker \phi _m$
.
$\ker \phi _m$
.
The assumption in Theorem 3.1 that v is primitive is necessary for
![]() $G_A(v)$
to be isomorphic to
$G_A(v)$
to be isomorphic to
![]() $({\mathbb Z}/n{\mathbb Z})^4$
. In the case where
$({\mathbb Z}/n{\mathbb Z})^4$
. In the case where
![]() $v=2v_0$
for
$v=2v_0$
for
![]() $v_0$
a primitive Mukai vector with
$v_0$
a primitive Mukai vector with
![]() $v_0^2=2$
, which is used to construct O’Grady sixfolds, the solutions to the equations (3.1) are precisely of the form
$v_0^2=2$
, which is used to construct O’Grady sixfolds, the solutions to the equations (3.1) are precisely of the form
![]() $(A\times \hat {A})[2]\cong ({\mathbb Z}/2{\mathbb Z})^8$
, as is shown in [Reference Mukai42, Lem. 5.1]. We generalize this result by extending Theorem 3.1 to find all solutions to (3.1) for any Mukai vector.
$(A\times \hat {A})[2]\cong ({\mathbb Z}/2{\mathbb Z})^8$
, as is shown in [Reference Mukai42, Lem. 5.1]. We generalize this result by extending Theorem 3.1 to find all solutions to (3.1) for any Mukai vector.
In the following result, we alter our hypotheses by naming the primitive vector of Setting 2.4
![]() $v_0$
and considering a multiple of
$v_0$
and considering a multiple of
![]() $v_0$
.
$v_0$
.
Corollary 3.8. Let
![]() $v=(r,l,s)$
be a Mukai vector on an abelian surface A so that
$v=(r,l,s)$
be a Mukai vector on an abelian surface A so that
![]() $v=dv_0$
, where
$v=dv_0$
, where
![]() $v_0=(r_0,l_0,s_0)$
is primitive and
$v_0=(r_0,l_0,s_0)$
is primitive and
![]() $n:=\frac {v_0^2}{2}$
.
$n:=\frac {v_0^2}{2}$
.
Then, the group
![]() $G_A(v)$
of solutions
$G_A(v)$
of solutions
![]() $(x,y)\in A\times \hat {A}$
to the following equations
$(x,y)\in A\times \hat {A}$
to the following equations
is isomorphic to
![]() $({\mathbb Z}/dn{\mathbb Z})^4\times ({\mathbb Z}/d{\mathbb Z})^4$
.
$({\mathbb Z}/dn{\mathbb Z})^4\times ({\mathbb Z}/d{\mathbb Z})^4$
.
Proof. Let m and
![]() $m_0$
be the respective Néron-Severi classes determined by
$m_0$
be the respective Néron-Severi classes determined by
![]() $\Phi _P$
. We see from the definition of
$\Phi _P$
. We see from the definition of
![]() $\phi _l$
that
$\phi _l$
that
![]() $\phi _l=d\cdot \phi _{l_0}$
and likewise,
$\phi _l=d\cdot \phi _{l_0}$
and likewise,
![]() $\phi _m=d\cdot \phi _{m_0}$
: if we choose
$\phi _m=d\cdot \phi _{m_0}$
: if we choose
![]() $(L_0,M_0)\in \operatorname {\mathrm {Pic}}^{l_0}(A)\times \operatorname {\mathrm {Pic}}^{m_0}(\hat {A})$
and
$(L_0,M_0)\in \operatorname {\mathrm {Pic}}^{l_0}(A)\times \operatorname {\mathrm {Pic}}^{m_0}(\hat {A})$
and
![]() $L:=L_0^{\otimes d}$
,
$L:=L_0^{\otimes d}$
,
![]() $M:=M_0^{\otimes d}$
, then for any
$M:=M_0^{\otimes d}$
, then for any
![]() $x\in A$
, we have
$x\in A$
, we have
Since
![]() $\phi _{l_0}$
and
$\phi _{l_0}$
and
![]() $\phi _{m_0}$
are group homomorphisms, we have, for any
$\phi _{m_0}$
are group homomorphisms, we have, for any
![]() $(x,y)\in A \times \hat {A}$
,
$(x,y)\in A \times \hat {A}$
,
Thus, a pair
![]() $(x,y)\in A\times \hat {A}$
is a solution to (3.7) if and only if
$(x,y)\in A\times \hat {A}$
is a solution to (3.7) if and only if
or equivalently,
![]() $(dx,dy)$
solves the equations (3.1) given by
$(dx,dy)$
solves the equations (3.1) given by
![]() $v_0$
. By Theorem 3.1, the set of solutions to the equations (3.1) given by
$v_0$
. By Theorem 3.1, the set of solutions to the equations (3.1) given by
![]() $v_0$
is isomorphic to
$v_0$
is isomorphic to
![]() $({\mathbb Z}/n{\mathbb Z})^4\cong G_A(v_0)$
. We may conclude by observing that the set of solutions to (3.7) is given by exactly the elements of
$({\mathbb Z}/n{\mathbb Z})^4\cong G_A(v_0)$
. We may conclude by observing that the set of solutions to (3.7) is given by exactly the elements of
![]() $A\times \hat {A}$
that are in
$A\times \hat {A}$
that are in
![]() $G_A(v_0)$
after being multiplied by d.
$G_A(v_0)$
after being multiplied by d.
3.2 Involutions and fixed loci
Let A be an abelian surface over an arbitrary field k. If
![]() $K_A(v)$
is a fiber over symmetric line bundles, then
$K_A(v)$
is a fiber over symmetric line bundles, then
![]() $\iota ^*$
gives an involution of
$\iota ^*$
gives an involution of
![]() $K_A(v)$
. However, if symmetric bundles do not exist in the appropriate Néron-Severi classes over k, we show here how to define an involution
$K_A(v)$
. However, if symmetric bundles do not exist in the appropriate Néron-Severi classes over k, we show here how to define an involution
![]() $\kappa $
to replace
$\kappa $
to replace
![]() $\iota ^*$
. For the remainder of the section, we fix a set of data as in Setting 2.4 and hence, fix a variety
$\iota ^*$
. For the remainder of the section, we fix a set of data as in Setting 2.4 and hence, fix a variety
![]() $K_A(v)$
over k.
$K_A(v)$
over k.
We first give a lemma that will allow us to construct the involution
![]() $\kappa $
.
$\kappa $
.
Lemma 3.9. Suppose we have an additional choice of line bundles
![]() $L'\in \operatorname {\mathrm {Pic}}^l(A)$
,
$L'\in \operatorname {\mathrm {Pic}}^l(A)$
,
![]() $M'\in \operatorname {\mathrm {Pic}}^m(\hat {A})$
over k. Let
$M'\in \operatorname {\mathrm {Pic}}^m(\hat {A})$
over k. Let
![]() $K_A(v)':=\operatorname {\mathrm {alb}}^{-1}(L',M')$
. Then, there is an element
$K_A(v)':=\operatorname {\mathrm {alb}}^{-1}(L',M')$
. Then, there is an element
![]() $(a,b)\in (A\times \hat {A})(k)$
so that
$(a,b)\in (A\times \hat {A})(k)$
so that
![]() $L_b\otimes t_a^*\colon K_A(v) \to K_A(v)'$
is an isomorphism over k. It is unique up to composition with elements in
$L_b\otimes t_a^*\colon K_A(v) \to K_A(v)'$
is an isomorphism over k. It is unique up to composition with elements in
![]() $G_A(v)(k)$
.
$G_A(v)(k)$
.
Proof. Recall that for any
![]() $(x,y)\in A\times \hat {A}$
, applying
$(x,y)\in A\times \hat {A}$
, applying
![]() $L_y\otimes t_x^*$
to an element
$L_y\otimes t_x^*$
to an element
![]() $\mathcal F\in K_A(v)$
, we have
$\mathcal F\in K_A(v)$
, we have
We also recall that the morphism
![]() $\phi \colon A\times \hat {A} \to A \times \hat {A}$
from (3.2) is an isogeny defined over k and sends sends
$\phi \colon A\times \hat {A} \to A \times \hat {A}$
from (3.2) is an isogeny defined over k and sends sends
![]() $(x,y)$
to
$(x,y)$
to
The element
![]() $(a,b)$
desired is precisely a preimage of
$(a,b)$
desired is precisely a preimage of
![]() $(L'\otimes L^{-1},M'\otimes M^{-1})\in (A\times \hat {A})(k)$
under
$(L'\otimes L^{-1},M'\otimes M^{-1})\in (A\times \hat {A})(k)$
under
![]() $\phi $
. Finally,
$\phi $
. Finally,
![]() $L_b\otimes t_a^*: K_A(v) \to K_A(v)'$
is an isomorphism since it has an inverse
$L_b\otimes t_a^*: K_A(v) \to K_A(v)'$
is an isomorphism since it has an inverse
![]() $L_{-b}\otimes t_{-a}^*$
.
$L_{-b}\otimes t_{-a}^*$
.
Construction 3.10. Applying
![]() $\iota ^*$
gives an isomorphism from
$\iota ^*$
gives an isomorphism from
![]() $K_A(v)$
to
$K_A(v)$
to
![]() $\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
. By Lemma 3.9, there is an
$\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
. By Lemma 3.9, there is an
![]() $(a,b)\in (A\times \hat {A})(k)$
such that
$(a,b)\in (A\times \hat {A})(k)$
such that
![]() $L_b\otimes t_a^*$
maps isomorphically from
$L_b\otimes t_a^*$
maps isomorphically from
![]() $\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
back to
$\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
back to
![]() $K_A(v)$
. So we have the following automorphism defined over k:
$K_A(v)$
. So we have the following automorphism defined over k:
 $$ \begin{align*} \kappa\colon K_A(v)&\to K_A(v)\\ \mathcal F&\mapsto L_b\otimes t_a^*\iota^*{\mathcal F}. \end{align*} $$
$$ \begin{align*} \kappa\colon K_A(v)&\to K_A(v)\\ \mathcal F&\mapsto L_b\otimes t_a^*\iota^*{\mathcal F}. \end{align*} $$
Remark 3.11. We note that
![]() $\kappa $
is an involution. More generally, for any
$\kappa $
is an involution. More generally, for any
![]() $(c,d)\in A\times \hat {A}$
, the morphism
$(c,d)\in A\times \hat {A}$
, the morphism
![]() $L_d\otimes t_c^*\iota ^*$
(which in general is an automorphism of
$L_d\otimes t_c^*\iota ^*$
(which in general is an automorphism of
![]() $M(v)$
but perhaps not of
$M(v)$
but perhaps not of
![]() $K(v)$
) is an involution on
$K(v)$
) is an involution on
![]() $M_A(v)$
. Indeed,
$M_A(v)$
. Indeed,
![]() $(\iota \circ t_c)^2=\operatorname {\mathrm {id}}$
on A and
$(\iota \circ t_c)^2=\operatorname {\mathrm {id}}$
on A and
![]() $L_d$
is degree
$L_d$
is degree
![]() $0$
and hence, fixed under pullback by translation; thus, for any
$0$
and hence, fixed under pullback by translation; thus, for any
![]() $\mathcal F\in M_A(v)$
, we have:
$\mathcal F\in M_A(v)$
, we have:
 $$ \begin{align*} (L_d\otimes t_c^*\iota^*)\circ (L_d\otimes t_c^*\iota^*)(\mathcal F) &=L_d\otimes t_c^*\iota^*L_d \otimes t_c^*\iota^*t_c^*\iota^*(\mathcal F)\\ &=L_d\otimes t_c^*L_d^{-1} \otimes \mathcal F =L_d\otimes L_d^{-1} \otimes \mathcal F=\mathcal F. \end{align*} $$
$$ \begin{align*} (L_d\otimes t_c^*\iota^*)\circ (L_d\otimes t_c^*\iota^*)(\mathcal F) &=L_d\otimes t_c^*\iota^*L_d \otimes t_c^*\iota^*t_c^*\iota^*(\mathcal F)\\ &=L_d\otimes t_c^*L_d^{-1} \otimes \mathcal F =L_d\otimes L_d^{-1} \otimes \mathcal F=\mathcal F. \end{align*} $$
The following are thus involutions of
![]() $K_A(v)$
, where
$K_A(v)$
, where
![]() $(x,y)\in G_A(v)(k)$
:
$(x,y)\in G_A(v)(k)$
:
Under the simplifying assumption that L and M are symmetric, we may instead denote these involutions as
Lemma 3.12. Let
![]() $n:=\frac {v^2}{2}$
be odd. Assume
$n:=\frac {v^2}{2}$
be odd. Assume
![]() $k=\bar {k}$
and that L and M are symmetric, so
$k=\bar {k}$
and that L and M are symmetric, so
![]() $\iota ^*$
is an involution on
$\iota ^*$
is an involution on
![]() $K_A(v)$
. Then,
$K_A(v)$
. Then,
![]() $\operatorname {\mathrm {Fix}}(\iota _{(x,y)})$
is a translation of
$\operatorname {\mathrm {Fix}}(\iota _{(x,y)})$
is a translation of
![]() $\operatorname {\mathrm {Fix}}(\iota _{(0,0)})$
; that is, there exists
$\operatorname {\mathrm {Fix}}(\iota _{(0,0)})$
; that is, there exists
![]() $(u,w)\in G_A(v)$
so that
$(u,w)\in G_A(v)$
so that
More generally, without the assumption that L and M are symmetric, there exists
![]() $(u,w)\in G_A(v)$
so that
$(u,w)\in G_A(v)$
so that
Proof. Let
![]() $\mathcal F\in K_A(v)$
be in the fixed locus of
$\mathcal F\in K_A(v)$
be in the fixed locus of
![]() $\iota ^*$
. Pick
$\iota ^*$
. Pick
![]() $(u,w)\in G_A(v)$
so that
$(u,w)\in G_A(v)$
so that
![]() $2w=y$
and
$2w=y$
and
![]() $2u=x$
, which is possible since n is odd. For instance, when
$2u=x$
, which is possible since n is odd. For instance, when
![]() $\frac {v^2}{2}=3$
,
$\frac {v^2}{2}=3$
,
![]() $K_A(v)$
is a fourfold and the elements of
$K_A(v)$
is a fourfold and the elements of
![]() $G_A(v)$
are all three-torsion, so we may choose
$G_A(v)$
are all three-torsion, so we may choose
![]() $(-x,-y)$
.
$(-x,-y)$
.
Then,
![]() $L_{w}\otimes t_{u}^*\mathcal F$
must be fixed by the involution
$L_{w}\otimes t_{u}^*\mathcal F$
must be fixed by the involution
The other direction of the containment is similar, as is the case with
![]() $\iota ^*$
replaced by
$\iota ^*$
replaced by
![]() $\kappa $
.
$\kappa $
.
Proposition 3.13. Let
![]() $n:=\frac {v^2}{2}$
be odd, assume
$n:=\frac {v^2}{2}$
be odd, assume
![]() $k=\bar {k}$
and let
$k=\bar {k}$
and let
![]() $L'\in \operatorname {\mathrm {Pic}}^l(A)$
and
$L'\in \operatorname {\mathrm {Pic}}^l(A)$
and
![]() $M'\in \operatorname {\mathrm {Pic}}^m(\hat {A})$
be symmetric line bundles (cf. Lemma 2.6). Fix an involution
$M'\in \operatorname {\mathrm {Pic}}^m(\hat {A})$
be symmetric line bundles (cf. Lemma 2.6). Fix an involution
![]() $\kappa $
as in Construction 3.10 on
$\kappa $
as in Construction 3.10 on
![]() $K_A(v)$
. Then, the fixed locus of
$K_A(v)$
. Then, the fixed locus of
![]() $\kappa $
in
$\kappa $
in
![]() $K_A(v)$
is isomorphic to the fixed locus of
$K_A(v)$
is isomorphic to the fixed locus of
![]() $\iota ^*=\iota _{(0,0)}$
in
$\iota ^*=\iota _{(0,0)}$
in
![]() $K_A(v)'$
.
$K_A(v)'$
.
Proof. By Lemma 3.9, there is an
![]() $(x,y)\in A\times \hat {A}$
so that
$(x,y)\in A\times \hat {A}$
so that
![]() $L_y\otimes t_x^*$
gives an isomorphism from
$L_y\otimes t_x^*$
gives an isomorphism from
![]() $K_A(v)$
to
$K_A(v)$
to
![]() $K_A(v)'$
. The composition
$K_A(v)'$
. The composition
may be rearranged to
![]() $L_{-2y}\otimes t_{-2x}^*\iota ^*$
, where
$L_{-2y}\otimes t_{-2x}^*\iota ^*$
, where
![]() $L_{-2y}\otimes t_{-2x}^*$
gives an isomorphism from
$L_{-2y}\otimes t_{-2x}^*$
gives an isomorphism from
![]() $\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
to
$\operatorname {\mathrm {alb}}^{-1}(\iota ^*L,\iota ^*M)$
to
![]() $K_A(v)$
. Thus, by the uniqueness statement of Lemma 3.9, there is an element
$K_A(v)$
. Thus, by the uniqueness statement of Lemma 3.9, there is an element
![]() $(u,w)\in G_A(v)$
for which
$(u,w)\in G_A(v)$
for which
![]() $L_w\otimes t_u^*\circ L_{-2y}\otimes t_{-2x}^*$
is equal to the map
$L_w\otimes t_u^*\circ L_{-2y}\otimes t_{-2x}^*$
is equal to the map
![]() $L_{b}\otimes t_{a}^*$
in the definition of
$L_{b}\otimes t_{a}^*$
in the definition of
![]() $\kappa $
. Then,
$\kappa $
. Then,
![]() $L_{-y}\otimes t_{-x}^* \operatorname {\mathrm {Fix}}(\iota ^*)$
is equal to
$L_{-y}\otimes t_{-x}^* \operatorname {\mathrm {Fix}}(\iota ^*)$
is equal to
![]() $\operatorname {\mathrm {Fix}}(\kappa _{(-u,-w)})$
, which is isomorphic to
$\operatorname {\mathrm {Fix}}(\kappa _{(-u,-w)})$
, which is isomorphic to
![]() $\operatorname {\mathrm {Fix}}(\kappa )$
by Lemma 3.12.
$\operatorname {\mathrm {Fix}}(\kappa )$
by Lemma 3.12.
Finally, we give the following general result on the action of the Galois group on the geometric fixed loci.
Proposition 3.14. Let k be an arbitrary field. For
![]() $(x,y)\in G_{A_{{\bar {k}}}}(v)$
, the action of
$(x,y)\in G_{A_{{\bar {k}}}}(v)$
, the action of
![]() $\sigma \in \operatorname {\mathrm {Gal}}(k/k)$
sends the fixed locus of
$\sigma \in \operatorname {\mathrm {Gal}}(k/k)$
sends the fixed locus of
![]() $\kappa _{(x,y)}$
in
$\kappa _{(x,y)}$
in
![]() $K_A(v)_{\bar {k}}$
to the fixed locus of
$K_A(v)_{\bar {k}}$
to the fixed locus of
![]() $\kappa _{(\sigma ^{-1} x,\sigma ^{-1} y)}$
.
$\kappa _{(\sigma ^{-1} x,\sigma ^{-1} y)}$
.
Proof. Suppose
![]() $\mathcal F$
is fixed by
$\mathcal F$
is fixed by
![]() $\kappa _{(x,y)}$
. We use the equality
$\kappa _{(x,y)}$
. We use the equality
![]() $t_x\circ \sigma =\sigma \circ t_{\sigma ^{-1}x}$
and the observation that
$t_x\circ \sigma =\sigma \circ t_{\sigma ^{-1}x}$
and the observation that
![]() $\sigma $
commutes with
$\sigma $
commutes with
![]() $\iota $
and, moreover,
$\iota $
and, moreover,
![]() $\kappa $
, since
$\kappa $
, since
![]() $\kappa $
is defined over the ground field k, to simplify the following equation:
$\kappa $
is defined over the ground field k, to simplify the following equation:
Then, we have
![]() $\sigma ^*L_y\simeq L_{\sigma ^{-1}y}$
, which we may verify using
$\sigma ^*L_y\simeq L_{\sigma ^{-1}y}$
, which we may verify using
![]() $\Phi _P\colon D(A)\to D(\hat {A})$
:
$\Phi _P\colon D(A)\to D(\hat {A})$
:
 $$ \begin{align*} \Phi_P(L_{-\sigma^{-1}y}\otimes \sigma^*L_y) &\simeq t_{-\sigma^{-1}y}^*\sigma^*k(-y)[-g] \simeq \sigma^*t_{-y}^*k(-y)[-g]\\ &\simeq\sigma^*k(0_{\hat{A}})[-g]\simeq k(0_{\hat{A}})[-g].\\[-38pt] \end{align*} $$
$$ \begin{align*} \Phi_P(L_{-\sigma^{-1}y}\otimes \sigma^*L_y) &\simeq t_{-\sigma^{-1}y}^*\sigma^*k(-y)[-g] \simeq \sigma^*t_{-y}^*k(-y)[-g]\\ &\simeq\sigma^*k(0_{\hat{A}})[-g]\simeq k(0_{\hat{A}})[-g].\\[-38pt] \end{align*} $$
3.3 Symplectic automorphisms and involutions
Let A be an abelian surface over
![]() ${\mathbb C}$
. In the following lemma, we give a generalization of [Reference Bolognesi and Massarenti8, Cor. 5(2)] to hyperkähler varieties
${\mathbb C}$
. In the following lemma, we give a generalization of [Reference Bolognesi and Massarenti8, Cor. 5(2)] to hyperkähler varieties
![]() $K_A(v)$
over
$K_A(v)$
over
![]() ${\mathbb C}$
.
${\mathbb C}$
.
Theorem 3.15. Suppose we are in Setting 2.4 and we fix an involution
![]() $\kappa $
as in Construction 3.10. Then, the kernel of
$\kappa $
as in Construction 3.10. Then, the kernel of
consists of automorphisms of the form
![]() $L_y\otimes t_x^*$
and of the form
$L_y\otimes t_x^*$
and of the form
![]() $\kappa _{(x,y)}:=L_y\otimes t_x^*\kappa $
for
$\kappa _{(x,y)}:=L_y\otimes t_x^*\kappa $
for
![]() $(x,y)\in G_A(v)$
. Thus, for any
$(x,y)\in G_A(v)$
. Thus, for any
![]() $(x,y)\in G_A(v)$
, the automorphism
$(x,y)\in G_A(v)$
, the automorphism
![]() $L_y\otimes t_x^*$
is symplectic. The
$L_y\otimes t_x^*$
is symplectic. The
![]() $\kappa _{(x,y)}$
are symplectic involutions of
$\kappa _{(x,y)}$
are symplectic involutions of
![]() $K_A(v)$
, and when
$K_A(v)$
, and when
![]() $\dim K_A(v)=4$
, these are all of the symplectic involutions.
$\dim K_A(v)=4$
, these are all of the symplectic involutions.
Remark 3.16. While
![]() $\kappa $
is not unique, by Lemma 3.9, the collection of elements in
$\kappa $
is not unique, by Lemma 3.9, the collection of elements in
![]() $\ker \nu $
is independent of the choice made in Construction 3.10.
$\ker \nu $
is independent of the choice made in Construction 3.10.
Proof. Elements of
![]() $(x,y)\in A\times \hat {A}$
act on
$(x,y)\in A\times \hat {A}$
act on
![]() $M_A(v)$
via
$M_A(v)$
via
![]() $L_{y}\otimes t_{x}^*$
. Abelian varieties are path-connected, so the action of any element in
$L_{y}\otimes t_{x}^*$
. Abelian varieties are path-connected, so the action of any element in
![]() $A\times \hat {A}$
is homotopic to the identity, which implies the induced action on
$A\times \hat {A}$
is homotopic to the identity, which implies the induced action on
![]() $H^2(M_A(v),{\mathbb Z})$
is trivial. If
$H^2(M_A(v),{\mathbb Z})$
is trivial. If
![]() $(x,y)\in G_A(v)$
, then Theorem 3.1 shows that the action of
$(x,y)\in G_A(v)$
, then Theorem 3.1 shows that the action of
![]() $L_{y}\otimes t_{x}^*$
restricts to
$L_{y}\otimes t_{x}^*$
restricts to
![]() $K_A(v)$
. By [Reference Yoshioka56, Thm. 0.2(2)], the restriction map
$K_A(v)$
. By [Reference Yoshioka56, Thm. 0.2(2)], the restriction map
![]() $H^2(M_A(v),{\mathbb Z})\to H^2(K_A(v),{\mathbb Z})$
is a surjection. Therefore,
$H^2(M_A(v),{\mathbb Z})\to H^2(K_A(v),{\mathbb Z})$
is a surjection. Therefore,
![]() $L_{y}\otimes t_{x}^*$
acts trivially on
$L_{y}\otimes t_{x}^*$
acts trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
as well.
$H^2(K_A(v),{\mathbb Z})$
as well.
By [Reference Yoshioka56, Thm. 0.2(2)], there is an isomorphism
where
![]() $v^{\perp } \subset H^{even}(A,{\mathbb Z})$
is the orthogonal complement to v under the Mukai pairing. Since
$v^{\perp } \subset H^{even}(A,{\mathbb Z})$
is the orthogonal complement to v under the Mukai pairing. Since
![]() $\iota ^*$
acts by
$\iota ^*$
acts by
![]() $-1$
on
$-1$
on
![]() $H^1(A,{\mathbb Z})$
, it acts trivially on
$H^1(A,{\mathbb Z})$
, it acts trivially on
![]() $H^{even}(A,{\mathbb Z})$
.
$H^{even}(A,{\mathbb Z})$
.
If we assume L and M are symmetric,
![]() $\iota ^*$
is an automorphism of
$\iota ^*$
is an automorphism of
![]() $K_A(v)$
and therefore must act trivially on
$K_A(v)$
and therefore must act trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
. If L and M are not both symmetric, since we are working over an algebraically closed field, we observe that
$H^2(K_A(v),{\mathbb Z})$
. If L and M are not both symmetric, since we are working over an algebraically closed field, we observe that
![]() $\kappa $
is a composition of translation to an Albanese fiber over symmetric bundles, application of
$\kappa $
is a composition of translation to an Albanese fiber over symmetric bundles, application of
![]() $\iota ^*$
on that fiber and translation back (cf. proof of Proposition 3.13). Thus,
$\iota ^*$
on that fiber and translation back (cf. proof of Proposition 3.13). Thus,
![]() $\kappa $
will act trivially on
$\kappa $
will act trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
as well.
$H^2(K_A(v),{\mathbb Z})$
as well.
By the discussion above,
![]() $\ker \nu $
contains
$\ker \nu $
contains
![]() $2n^4$
elements, so by Theorem 3.1, we have identified all of them. The automorphisms in this kernel are clearly symplectic as the symplectic form generates part of
$2n^4$
elements, so by Theorem 3.1, we have identified all of them. The automorphisms in this kernel are clearly symplectic as the symplectic form generates part of
![]() $H^2(K_A(v),{\mathbb C})$
.
$H^2(K_A(v),{\mathbb C})$
.
For any nontrivial choice of
![]() $(x,y)\in G_A(v)$
,
$(x,y)\in G_A(v)$
,
![]() $L_y\otimes t_x^*$
is not an involution, but by Section 3.2,
$L_y\otimes t_x^*$
is not an involution, but by Section 3.2,
![]() $\kappa _{(x,y)}$
is an involution on
$\kappa _{(x,y)}$
is an involution on
![]() $K_A(v)$
.
$K_A(v)$
.
Finally, suppose
![]() $\dim K_A(v)=4$
. By [Reference Kass31, Thm. 7.5(i)], all of the symplectic involutions of
$\dim K_A(v)=4$
. By [Reference Kass31, Thm. 7.5(i)], all of the symplectic involutions of
![]() $K_A(v)$
act trivially on
$K_A(v)$
act trivially on
![]() $H^2(K_A(v),{\mathbb Z})$
.
$H^2(K_A(v),{\mathbb Z})$
.
4 The middle cohomology of fourfolds
 $K_A(v)$
$K_A(v)$
In this section, we work with data as in Setting 2.4 with the additional assumption that
![]() $v^2=6$
, so
$v^2=6$
, so
![]() $K_A(v)$
is a fourfold. We will prove results characterizing the middle cohomology of
$K_A(v)$
is a fourfold. We will prove results characterizing the middle cohomology of
![]() $K_A(v)$
when k has characteristic
$K_A(v)$
when k has characteristic
![]() $0$
in Section 4.1. We use these results to characterize the cohomology similarly when k has positive characteristic in Section 4.2 via a brief lifting argument.
$0$
in Section 4.1. We use these results to characterize the cohomology similarly when k has positive characteristic in Section 4.2 via a brief lifting argument.
4.1 Results in characteristic zero
Assume
![]() $K_A(v)$
is defined over an arbitrary field k of characteristic zero, so we may assume without loss of generality that
$K_A(v)$
is defined over an arbitrary field k of characteristic zero, so we may assume without loss of generality that
![]() $\bar {k} \hookrightarrow {\mathbb C}$
. In this case, we can identify the Galois representations which make up the middle cohomology of
$\bar {k} \hookrightarrow {\mathbb C}$
. In this case, we can identify the Galois representations which make up the middle cohomology of
![]() $K_A(v)$
. This will depend on understanding the fixed loci of
$K_A(v)$
. This will depend on understanding the fixed loci of
![]() $\kappa _{(x,y)}$
for
$\kappa _{(x,y)}$
for
![]() $(x,y)\in G_{A_{\bar {k}}}(v)$
.
$(x,y)\in G_{A_{\bar {k}}}(v)$
.
Proposition 4.1. Suppose
![]() $k={\bar {k}}$
. The fixed locus of any involution
$k={\bar {k}}$
. The fixed locus of any involution
![]() $\kappa _{(x,y)}$
for
$\kappa _{(x,y)}$
for
![]() $(x,y)\in G_A(v)$
on a fourfold
$(x,y)\in G_A(v)$
on a fourfold
![]() $K_A(v)$
consists of a K3 surface and 36 isolated points.
$K_A(v)$
consists of a K3 surface and 36 isolated points.
Proof. First, suppose
![]() $k={\mathbb C}$
. Work of Hassett and Tschinkel [Reference Honigs21] and Tarí [Reference Tarí54] shows that the statement is true for
$k={\mathbb C}$
. Work of Hassett and Tschinkel [Reference Honigs21] and Tarí [Reference Tarí54] shows that the statement is true for
![]() $K_2(A)$
. A discussion of the isolated fixed points in this case is given in Section 6.1.
$K_2(A)$
. A discussion of the isolated fixed points in this case is given in Section 6.1.
Every hyperkähler fourfold
![]() $K_A(v)$
is deformation equivalent to
$K_A(v)$
is deformation equivalent to
![]() $K_2(A)$
and by [Reference Honigs21, Thm. 2.1], its group of symplectic involutions is also a deformation invariant. Thus, as in Kapfer and Menet [Reference Kass31, Thm. 7.5], the fixed loci are related by deformation as well, so the statement holds for
$K_2(A)$
and by [Reference Honigs21, Thm. 2.1], its group of symplectic involutions is also a deformation invariant. Thus, as in Kapfer and Menet [Reference Kass31, Thm. 7.5], the fixed loci are related by deformation as well, so the statement holds for
![]() $K_A(v)$
.
$K_A(v)$
.
Now let k be any algebraically closed field of characteristic zero. Since A is defined over k, we can assume without loss of generality that
![]() $k \hookrightarrow {\mathbb C}$
. Let
$k \hookrightarrow {\mathbb C}$
. Let
![]() ${K}_A(v)_{{\mathbb C}} := K_A(v) \times _{k} {\mathbb C}$
and consider the Cartesian square
${K}_A(v)_{{\mathbb C}} := K_A(v) \times _{k} {\mathbb C}$
and consider the Cartesian square

where
![]() $\widetilde {\kappa }_{(x,y)}$
is formed by replacing
$\widetilde {\kappa }_{(x,y)}$
is formed by replacing
![]() $\kappa $
with its extension to
$\kappa $
with its extension to
![]() ${\mathbb C}$
, which we call
${\mathbb C}$
, which we call
![]() $\tilde {\kappa }$
. By Theorem 3.15,
$\tilde {\kappa }$
. By Theorem 3.15,
![]() $\widetilde {\kappa }_{(x,y)}$
is a symplectic involution, and by the argument above,
$\widetilde {\kappa }_{(x,y)}$
is a symplectic involution, and by the argument above,
![]() $\operatorname {\mathrm {Fix}}(\widetilde {\kappa }_{(x,y)})$
is a K3 surface
$\operatorname {\mathrm {Fix}}(\widetilde {\kappa }_{(x,y)})$
is a K3 surface
![]() $Z:=Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
plus 36 isolated points.
$Z:=Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
plus 36 isolated points.
By [Reference Frei14, Rmk. 3 following Thm 2.3],
This descent of the fixed-point locus means that
![]() $\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
consists of a surface
$\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
consists of a surface
![]() $S:=S_{(x,y)}\subset K_A(v)$
along with 36 k-points. We claim that S is a K3 surface. Indeed, we see via the valuative criterion of properness, using the fact that
$S:=S_{(x,y)}\subset K_A(v)$
along with 36 k-points. We claim that S is a K3 surface. Indeed, we see via the valuative criterion of properness, using the fact that
![]() $\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
is a closed subscheme of
$\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
is a closed subscheme of
![]() $K_A(v)$
, that
$K_A(v)$
, that
![]() $S \to \operatorname {\mathrm {Spec}} k$
is proper. By flat base change, we have that
$S \to \operatorname {\mathrm {Spec}} k$
is proper. By flat base change, we have that
![]() $H^1(S,\mathcal {O}_S)\otimes {\mathbb C} \cong H^1(Z,\mathcal {O}_{Z})=0$
, and
$H^1(S,\mathcal {O}_S)\otimes {\mathbb C} \cong H^1(Z,\mathcal {O}_{Z})=0$
, and
![]() $H^0(S,\omega _S)\otimes {\mathbb C} \cong H^0(Z,\omega _{Z})={\mathbb C}$
, so
$H^0(S,\omega _S)\otimes {\mathbb C} \cong H^0(Z,\omega _{Z})={\mathbb C}$
, so
![]() $\omega _S$
has a nonvanishing global section and hence, is trivial. Finally, S is smooth by [Reference Esteves11, Lem. 4.1], which completes the proof.
$\omega _S$
has a nonvanishing global section and hence, is trivial. Finally, S is smooth by [Reference Esteves11, Lem. 4.1], which completes the proof.
See [Reference Kapfer and Menet30] for further discussion of these fixed-point loci in hyperkählers of Kummer type.
Let k now be arbitrary. Let
![]() $S_{(x,y)}\subset K_A(v)_{\bar {k}}$
be the K3 surface in
$S_{(x,y)}\subset K_A(v)_{\bar {k}}$
be the K3 surface in
![]() $\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
and
$\operatorname {\mathrm {Fix}}(\kappa _{(x,y)})$
and
![]() $s_{(x,y)}\in H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
the image of
$s_{(x,y)}\in H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
the image of
![]() $[S_{(x,y)}]\in \operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}}$
under the cycle class map
$[S_{(x,y)}]\in \operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}}$
under the cycle class map
![]() $\operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}} \to H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
.
$\operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}} \to H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
.
Lemma 4.2. For
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\bar {k}/k)$
, the induced action on the cycle classes
$\sigma \in \operatorname {\mathrm {Gal}}(\bar {k}/k)$
, the induced action on the cycle classes
![]() $s_{(x,y)}$
for
$s_{(x,y)}$
for
![]() $(x,y)\in G_{A_{\bar {k}}}(v)$
is given by
$(x,y)\in G_{A_{\bar {k}}}(v)$
is given by
Proof. By [Reference Mongardi and Wandel40, Prop. 9.2], the cycle class map is Galois equivariant, so
![]() $\sigma ^*s_{(x,y)}$
is the cycle class of
$\sigma ^*s_{(x,y)}$
is the cycle class of
![]() $[\sigma ^* S_{(x,y)}]\in \operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}}$
. As in the proof of [Reference Mongardi and Wandel40, Prop. 9.2], we have that
$[\sigma ^* S_{(x,y)}]\in \operatorname {\mathrm {CH}}^2 K_A(v)_{\bar {k}}$
. As in the proof of [Reference Mongardi and Wandel40, Prop. 9.2], we have that
![]() $[\sigma ^* S_{(x,y)}]$
is the preimage of
$[\sigma ^* S_{(x,y)}]$
is the preimage of
![]() $S_{(x,y)}$
under
$S_{(x,y)}$
under
![]() $\sigma ^*\colon K_A(v)_{\bar {k}} \to K_A(v)_{\bar {k}}$
. By Proposition 3.14,
$\sigma ^*\colon K_A(v)_{\bar {k}} \to K_A(v)_{\bar {k}}$
. By Proposition 3.14,
![]() $(\sigma ^*)^{-1}(S_{(x,y)})=S_{(\sigma x, \sigma y)}$
. Thus, we conclude that
$(\sigma ^*)^{-1}(S_{(x,y)})=S_{(\sigma x, \sigma y)}$
. Thus, we conclude that
![]() $\sigma ^*s_{(x,y)}=s_{(\sigma x, \sigma y)}$
, as desired.
$\sigma ^*s_{(x,y)}=s_{(\sigma x, \sigma y)}$
, as desired.
Definition 4.3. For a finite Galois module G, let
![]() ${\mathbb Q}_{\ell }[G]$
be the
${\mathbb Q}_{\ell }[G]$
be the
![]() ${\mathbb Q}_{\ell }$
-vector space with basis given by G, where the action of the Galois group on
${\mathbb Q}_{\ell }$
-vector space with basis given by G, where the action of the Galois group on
![]() ${\mathbb Q}_{\ell }[G]$
is determined by the action on G: for
${\mathbb Q}_{\ell }[G]$
is determined by the action on G: for
![]() $\sigma \in \operatorname {\mathrm {Gal}}({\bar {k}}/k)$
and
$\sigma \in \operatorname {\mathrm {Gal}}({\bar {k}}/k)$
and
![]() $\sum _{g_i \in G} a_i g_i \in {\mathbb Q}_{\ell }[G]$
,
$\sum _{g_i \in G} a_i g_i \in {\mathbb Q}_{\ell }[G]$
,
 $$\begin{align*}\sigma \cdot \sum_{g_i \in G} a_i g_i = \sum_{g_i \in G} a_i \left(\sigma \cdot g_i\right).\end{align*}$$
$$\begin{align*}\sigma \cdot \sum_{g_i \in G} a_i g_i = \sum_{g_i \in G} a_i \left(\sigma \cdot g_i\right).\end{align*}$$
We call
![]() ${\mathbb Q}_{\ell }[G]$
the permutation representation.
${\mathbb Q}_{\ell }[G]$
the permutation representation.
Recall that when k is not algebraically closed, the group
![]() $G_{A_{{\bar {k}}}}(v)$
naturally has the structure of a finite
$G_{A_{{\bar {k}}}}(v)$
naturally has the structure of a finite
![]() $\operatorname {\mathrm {Gal}}({\bar {k}}/k)$
-module.
$\operatorname {\mathrm {Gal}}({\bar {k}}/k)$
-module.
Theorem 4.4. There is an isomorphism of Galois representations
where V is the
![]() $80$
-dimensional subrepresentation of
$80$
-dimensional subrepresentation of
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
and the trivial representation
![]() ${\mathbb Q}_{\ell }$
is the span of
${\mathbb Q}_{\ell }$
is the span of
![]() $(0,0)\in G_{A_{\bar {k}}}(v)$
.
$(0,0)\in G_{A_{\bar {k}}}(v)$
.
Remark 4.5. As will be shown in Lemma 5.7, the action of the Galois group on
![]() $H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
, and hence
$H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
, and hence
![]() $\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
, is determined by the action on
$\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
, is determined by the action on
![]() $H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))$
.
$H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))$
.
Proof. By Theorem 3.1, we have
![]() $3^4=81$
involutions
$3^4=81$
involutions
 $$ \begin{align*} \kappa_{(x,y)} \colon K_A(v)_{\bar{k}} &\to K_A(v)_{\bar{k}}\\ {\mathcal{F}} &\mapsto L_{y}\otimes t_{x}^*\kappa{\mathcal{F}}, \end{align*} $$
$$ \begin{align*} \kappa_{(x,y)} \colon K_A(v)_{\bar{k}} &\to K_A(v)_{\bar{k}}\\ {\mathcal{F}} &\mapsto L_{y}\otimes t_{x}^*\kappa{\mathcal{F}}, \end{align*} $$
where
![]() $(x,y)\in G_{A_{\bar {k}}}(v)$
.
$(x,y)\in G_{A_{\bar {k}}}(v)$
.
As in the proof of Proposition 4.1, let
![]() ${K}_A(v)_{{\mathbb C}} := K_A(v)\times _k {\mathbb C}$
and
${K}_A(v)_{{\mathbb C}} := K_A(v)\times _k {\mathbb C}$
and
![]() $\widetilde {\kappa }_{(x,y)}\colon {K}_A(v)_{{\mathbb C}} \to {K}_A(v)_{{\mathbb C}}$
the base change of
$\widetilde {\kappa }_{(x,y)}\colon {K}_A(v)_{{\mathbb C}} \to {K}_A(v)_{{\mathbb C}}$
the base change of
![]() $\kappa _{(x,y)}$
. By Proposition 4.1,
$\kappa _{(x,y)}$
. By Proposition 4.1,
![]() $\operatorname {\mathrm {Fix}}(\widetilde {\kappa }_{(x,y)})$
contains a K3 surface
$\operatorname {\mathrm {Fix}}(\widetilde {\kappa }_{(x,y)})$
contains a K3 surface
![]() $Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
. This gives 81 distinct K3 surfaces in
$Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
. This gives 81 distinct K3 surfaces in
![]() ${K}_A(v)_{{\mathbb C}}$
, where the distinctness follows from [Reference Honigs21, Thm. 2.1]. Via the cycle class map, these 81 surfaces give corresponding classes
${K}_A(v)_{{\mathbb C}}$
, where the distinctness follows from [Reference Honigs21, Thm. 2.1]. Via the cycle class map, these 81 surfaces give corresponding classes
![]() $z_{(x,y)}\in H^4({K}_A(v)_{{\mathbb C}}, {\mathbb Q})$
.
$z_{(x,y)}\in H^4({K}_A(v)_{{\mathbb C}}, {\mathbb Q})$
.
Similarly, there are K3 surfaces
![]() $S_{(x,y)}\subset K_A(v)_{\bar {k}}$
and corresponding cohomology classes
$S_{(x,y)}\subset K_A(v)_{\bar {k}}$
and corresponding cohomology classes
![]() $s_{(x,y)}\in H^4_{\mathrm {\acute{e}t}}({K}_A(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
such that
$s_{(x,y)}\in H^4_{\mathrm {\acute{e}t}}({K}_A(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
such that
![]() $S_{(x,y)}\times _{\bar {k}} {\mathbb C}= Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
. Under the comparison and smooth base change isomorphisms
$S_{(x,y)}\times _{\bar {k}} {\mathbb C}= Z_{(x,y)}\subset {K}_A(v)_{{\mathbb C}}$
. Under the comparison and smooth base change isomorphisms
the classes
![]() $z_{(x,y)}$
correspond to the classes
$z_{(x,y)}$
correspond to the classes
![]() $s_{(x,y)}$
.
$s_{(x,y)}$
.
By [Reference Kass31, Thm. 7.5(ii)], the pair
![]() $({K}_A(v)_{{\mathbb C}}, \widetilde {\kappa }_{(x,y)})$
is deformation equivalent to the pair
$({K}_A(v)_{{\mathbb C}}, \widetilde {\kappa }_{(x,y)})$
is deformation equivalent to the pair
![]() $(K_2(A_{{\mathbb C}}), t_{\tau }\circ [-\operatorname {\mathrm {Id}}]^{[[3]]})$
for some
$(K_2(A_{{\mathbb C}}), t_{\tau }\circ [-\operatorname {\mathrm {Id}}]^{[[3]]})$
for some
![]() $\tau \in A_{{\mathbb C}}[3]$
. In particular, these complex manifolds are diffeomorphic and so they have isomorphic cohomology rings. By [Reference Honigs21, Prop. 4.3] (see also the discussion in [Reference Kass31, §6.4]), the
$\tau \in A_{{\mathbb C}}[3]$
. In particular, these complex manifolds are diffeomorphic and so they have isomorphic cohomology rings. By [Reference Honigs21, Prop. 4.3] (see also the discussion in [Reference Kass31, §6.4]), the
![]() ${\mathbb Q}_{\ell }$
-span of
${\mathbb Q}_{\ell }$
-span of
![]() $\{z_{(x,y)}-z_{(0,0)}\}_{(x,y) \in G_{A_{\mathbb C}}(v)}$
is an 80-dimensional vector space of
$\{z_{(x,y)}-z_{(0,0)}\}_{(x,y) \in G_{A_{\mathbb C}}(v)}$
is an 80-dimensional vector space of
![]() $H^4(K_A(v)_{{\mathbb C}},{\mathbb Q}_{\ell }(2))$
which is a direct sum complement to the subspace
$H^4(K_A(v)_{{\mathbb C}},{\mathbb Q}_{\ell }(2))$
which is a direct sum complement to the subspace
![]() $\operatorname {\mathrm {Sym}}^2H^2(K_A(v)_{{\mathbb C}},{\mathbb Q}_{\ell }(1))$
.
$\operatorname {\mathrm {Sym}}^2H^2(K_A(v)_{{\mathbb C}},{\mathbb Q}_{\ell }(1))$
.
Since the
![]() $s_{(x,y)}$
in
$s_{(x,y)}$
in
![]() $H^4(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
correspond to the
$H^4(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
correspond to the
![]() $z_{(x,y)}$
, it follows that
$z_{(x,y)}$
, it follows that
is an
![]() $80$
-dimensional subspace of
$80$
-dimensional subspace of
![]() $H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
which is a direct sum complement to
$H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
which is a direct sum complement to
![]() $\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
.
$\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
.
By Lemma 4.2, we know that for
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\bar {k}/k)$
,
$\sigma \in \operatorname {\mathrm {Gal}}(\bar {k}/k)$
,
Thus, V is a Galois-invariant subspace of
![]() $H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
. Noting that
$H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
. Noting that
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
is semisimple by Maschke’s Theorem – the Galois action factors through a finite group representation determined by the finite extension of k over which
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
is semisimple by Maschke’s Theorem – the Galois action factors through a finite group representation determined by the finite extension of k over which
![]() $G_{A_{\bar {k}}}(v)$
is defined – and that
$G_{A_{\bar {k}}}(v)$
is defined – and that
![]() $\sigma ^*(s_{(0,0)})=s_{(0,0)}$
, this shows that V is the
$\sigma ^*(s_{(0,0)})=s_{(0,0)}$
, this shows that V is the
![]() $80$
-dimensional subrepresentation of
$80$
-dimensional subrepresentation of
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
where the trivial representation corresponds to
![]() $(0,0)\in G_{A_{\bar {k}}}(v)$
. Hence,
$(0,0)\in G_{A_{\bar {k}}}(v)$
. Hence,
![]() $H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
has the decomposition as stated.
$H^4_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(2))$
has the decomposition as stated.
4.2 Results in positive characteristic via lifting
In this section we observe that, because Kummer varieties
![]() $K_A(v)$
defined over a field of positive characteristic lift to characteristic
$K_A(v)$
defined over a field of positive characteristic lift to characteristic
![]() $0$
[Reference García and Lax17], we may use Theorem 4.4 to give a similar description of the middle cohomology.
$0$
[Reference García and Lax17], we may use Theorem 4.4 to give a similar description of the middle cohomology.
Proposition 4.6. Suppose we have data as in Setting 2.4, where the base field k has characteristic
![]() $p>0$
. Then,
$p>0$
. Then,
where
![]() $V'$
is the
$V'$
is the
![]() $80$
-dimensional subrepresentation of
$80$
-dimensional subrepresentation of
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
such that
and the trivial representation
![]() ${\mathbb Q}_{\ell }$
is the span of
${\mathbb Q}_{\ell }$
is the span of
![]() $(0,0)\in G_{A_{\bar {k}}}(v)$
.
$(0,0)\in G_{A_{\bar {k}}}(v)$
.
Proof. As explained in the proof of [Reference García and Lax17, Prop. 6.9], it is possible to lift
![]() $K_A(v)$
to characteristic
$K_A(v)$
to characteristic
![]() $0$
by lifting its defining data. That is, the data
$0$
by lifting its defining data. That is, the data
![]() $(A,v,H,L,M)$
defined over k has a lift
$(A,v,H,L,M)$
defined over k has a lift
![]() $(\mathcal {A}, v_W, \mathcal {H}, \mathcal {L}, \mathcal {M})$
to a complete discrete valuation ring W of characteristic zero with residue field k and field of fractions
$(\mathcal {A}, v_W, \mathcal {H}, \mathcal {L}, \mathcal {M})$
to a complete discrete valuation ring W of characteristic zero with residue field k and field of fractions
![]() $F:=\operatorname {\mathrm {Frac}} W$
. Note that all of this lifting data can be recovered from a lift of
$F:=\operatorname {\mathrm {Frac}} W$
. Note that all of this lifting data can be recovered from a lift of
![]() $(A,H,L)$
. Indeed, lifting A automatically gives us a lift of
$(A,H,L)$
. Indeed, lifting A automatically gives us a lift of
![]() $\hat {A}$
, and lifting line bundles on
$\hat {A}$
, and lifting line bundles on
![]() $\hat {A}$
amounts to lifting their Néron–Severi class; a lift of the Néron–Severi class of M is given by the Néron–Severi class of
$\hat {A}$
amounts to lifting their Néron–Severi class; a lift of the Néron–Severi class of M is given by the Néron–Severi class of
![]() $\det (\Phi _{\mathcal P}(\mathcal {L}))$
. Call the specialization of
$\det (\Phi _{\mathcal P}(\mathcal {L}))$
. Call the specialization of
![]() $v_W$
to the generic fiber
$v_W$
to the generic fiber
![]() $v_F$
.
$v_F$
.
There is a surjection of Galois groups
which is given by restricting automorphisms to the ring of integers of
![]() $\bar {F}$
and then passing to the quotient
$\bar {F}$
and then passing to the quotient
![]() $\bar {k}$
. By the smooth base change theorem [Reference Altman and Kleiman1, Exp. XVI, Corollaire 2.2], for
$\bar {k}$
. By the smooth base change theorem [Reference Altman and Kleiman1, Exp. XVI, Corollaire 2.2], for
![]() $\ell \neq p$
, there are isomorphisms
$\ell \neq p$
, there are isomorphisms
 $$ \begin{align} \begin{aligned} H^2_{\mathrm {\acute{e}t}}(K_{A_{\bar{F}}}(v_F), {\mathbb Q}_{\ell}(1)) &\cong H^2_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar{k}}, {\mathbb Q}_{\ell}(1)),\text{ and}\\ H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar{F}}}(v_F), {\mathbb Q}_{\ell}(2)) &\cong H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar{k}}, {\mathbb Q}_{\ell}(2)), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} H^2_{\mathrm {\acute{e}t}}(K_{A_{\bar{F}}}(v_F), {\mathbb Q}_{\ell}(1)) &\cong H^2_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar{k}}, {\mathbb Q}_{\ell}(1)),\text{ and}\\ H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar{F}}}(v_F), {\mathbb Q}_{\ell}(2)) &\cong H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar{k}}, {\mathbb Q}_{\ell}(2)), \end{aligned} \end{align} $$
which are equivariant with respect to the action of
![]() $\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on the left and
$\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on the left and
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on the right, compatible with (4.1).
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on the right, compatible with (4.1).
The isomorphisms of (4.2) are compatible with the ring structure on cohomology, so the isomorphism
![]() $H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar {F}}}(v_F), {\mathbb Q}_{\ell }(2)) \cong H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
restricts to an isomorphism
$H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar {F}}}(v_F), {\mathbb Q}_{\ell }(2)) \cong H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
restricts to an isomorphism
which is again compatible with the respective Galois group actions.
Let the following be the decomposition given by Theorem 4.4:
and let
![]() $V' \subset H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
be the vector space complement to
$V' \subset H^4_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(2))$
be the vector space complement to
![]() $\operatorname {\mathrm {Sym}}^2 H^2_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(1))$
. Using the fact that V is a
$\operatorname {\mathrm {Sym}}^2 H^2_{\mathrm {\acute{e}t}}(K_{A}(v)_{\bar {k}}, {\mathbb Q}_{\ell }(1))$
. Using the fact that V is a
![]() $\operatorname {\mathrm {Gal}}(\bar {F}/F)$
subrepresentation of
$\operatorname {\mathrm {Gal}}(\bar {F}/F)$
subrepresentation of
![]() $H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar {F}}}(v_F), {\mathbb Q}_{\ell }(2))$
, we conclude that
$H^4_{\mathrm {\acute{e}t}}(K_{A_{\bar {F}}}(v_F), {\mathbb Q}_{\ell }(2))$
, we conclude that
as
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
representations. In particular, there is an isomorphism
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
representations. In particular, there is an isomorphism
![]() $V\cong V'$
which is equivariant with respect to the action of
$V\cong V'$
which is equivariant with respect to the action of
![]() $\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on the left and
$\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on the left and
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on the right, again compatible with (4.1).
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on the right, again compatible with (4.1).
The subgroup
![]() $G_{A_{\bar {F}}}(v_F)\leqslant (A_{\bar {F}}\times \hat {A}_{\bar {F}})[3]$
is given by equations (3.1) determined by
$G_{A_{\bar {F}}}(v_F)\leqslant (A_{\bar {F}}\times \hat {A}_{\bar {F}})[3]$
is given by equations (3.1) determined by
![]() $v_F$
, which is part of our lifted data. Thus, since the action of
$v_F$
, which is part of our lifted data. Thus, since the action of
![]() $\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on V is given by
$\operatorname {\mathrm {Gal}}(\bar {F}/F)$
on V is given by
![]() $G_{A_{\bar {F}}}(v)$
, the action of
$G_{A_{\bar {F}}}(v)$
, the action of
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on
![]() $V'$
must be the one determined analogously by
$V'$
must be the one determined analogously by
![]() $G_{A_{\bar {k}}}(v)$
.
$G_{A_{\bar {k}}}(v)$
.
5 Relation to derived equivalences
There are a number of results related to derived equivalences of smooth, projective symplectic varieties. For example, if X and Y are derived equivalent smooth complex projective surfaces, then
![]() $D(\operatorname {\mathrm {Hilb}}^nX)\cong D(\operatorname {\mathrm {Hilb}}^nY)$
[Reference Polishchuk51, Prop. 8]. If X and Y are K3 surfaces, then the converse holds, and if two moduli spaces of stable sheaves
$D(\operatorname {\mathrm {Hilb}}^nX)\cong D(\operatorname {\mathrm {Hilb}}^nY)$
[Reference Polishchuk51, Prop. 8]. If X and Y are K3 surfaces, then the converse holds, and if two moduli spaces of stable sheaves
![]() $M_X(v)$
and
$M_X(v)$
and
![]() $M_Y(v')$
are derived equivalent, then X and Y are also derived equivalent [Reference Birkenhake and Lange5, Cor. 9.7]. If X and Y are derived equivalent K3 surfaces over any field k, then the
$M_Y(v')$
are derived equivalent, then X and Y are also derived equivalent [Reference Birkenhake and Lange5, Cor. 9.7]. If X and Y are derived equivalent K3 surfaces over any field k, then the
![]() $\ell $
-adic étale cohomologies of any moduli
$\ell $
-adic étale cohomologies of any moduli
![]() $M_X(v)$
and
$M_X(v)$
and
![]() $M_Y(v')$
of equal dimension are isomorphic as
$M_Y(v')$
of equal dimension are isomorphic as
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
representations [Reference Frei, Honigs and Voight15, Thm. 2]. However, it is still an open question when such moduli are derived equivalent.
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
representations [Reference Frei, Honigs and Voight15, Thm. 2]. However, it is still an open question when such moduli are derived equivalent.
In the direction of symplectic varieties of Kummer type, complex abelian surfaces A and B are derived equivalent if and only if there is an isomorphism
![]() $K_1(A)\cong K_1(B)$
between their associated Kummer K3 surfaces [Reference Hudson and Barth24, Reference Stellari53]. This result has also been proved for abelian surfaces over fields of odd characteristic [Reference Magni36]; the relation between Kummer surfaces and twisted derived equivalence of abelian surfaces has been examined in [Reference Li and Zou35, Thm. 6.5.2]. While A and
$K_1(A)\cong K_1(B)$
between their associated Kummer K3 surfaces [Reference Hudson and Barth24, Reference Stellari53]. This result has also been proved for abelian surfaces over fields of odd characteristic [Reference Magni36]; the relation between Kummer surfaces and twisted derived equivalence of abelian surfaces has been examined in [Reference Li and Zou35, Thm. 6.5.2]. While A and
![]() $\hat {A}$
are always derived equivalent over their field of definition, it is not known exactly when there is a derived equivalence between the generalized Kummer fourfolds
$\hat {A}$
are always derived equivalent over their field of definition, it is not known exactly when there is a derived equivalence between the generalized Kummer fourfolds
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
. Recently, it was shown that, over an algebraically closed field of characteristic zero, they are derived equivalent when A has a polarization of exponent coprime to
$K_2(\hat {A})$
. Recently, it was shown that, over an algebraically closed field of characteristic zero, they are derived equivalent when A has a polarization of exponent coprime to
![]() $3$
[Reference Markman37, Theorem 1].
$3$
[Reference Markman37, Theorem 1].
Given these results, we ask the following two questions, which we examine in Sections 5.1 and 5.2, respectively.
Question 1. Suppose we have a derived equivalence of abelian surfaces
![]() $D^b(A)\cong D^b(B)$
. How do the groups
$D^b(A)\cong D^b(B)$
. How do the groups
![]() $G_A(v)$
introduced in Section 3 interact with the Rouquier isomorphism
$G_A(v)$
introduced in Section 3 interact with the Rouquier isomorphism
![]() $A\times \hat {A}\simeq B\times \hat {B}$
?
$A\times \hat {A}\simeq B\times \hat {B}$
?
Question 2. Under what conditions are irreducible symplectic fourfolds of Kummer type derived equivalent?
Throughout this section, we will assume we are working with data as in Setting 2.4 and that all varieties
![]() $K_A(v)$
are an Albanese fiber over symmetric line bundles.
$K_A(v)$
are an Albanese fiber over symmetric line bundles.
5.1 Compatibility with the Rouquier isomorphism
Proposition 5.1 (Rouquier, cf. [Reference Huybrechts26, Prop. 9.45])
Let A and B be abelian varieties and
![]() $F\colon D(A) \to D(B)$
a derived equivalence. There is an isomorphism
$F\colon D(A) \to D(B)$
a derived equivalence. There is an isomorphism
![]() $f \colon A\times \hat {A} \to B \times \hat {B}$
, called the Rouquier isomorphism, which maps
$f \colon A\times \hat {A} \to B \times \hat {B}$
, called the Rouquier isomorphism, which maps
![]() $(a,\alpha )\in A\times \hat {A}$
to the unique element
$(a,\alpha )\in A\times \hat {A}$
to the unique element
![]() $(b,\beta )\in B\times \hat {B}$
so that the following diagram commutes:
$(b,\beta )\in B\times \hat {B}$
so that the following diagram commutes:

The following proposition gives some results addressing Question 1.
Proposition 5.2. Let A and B be abelian surfaces over a field k, and let
![]() $v=(r,l,s)\in N(A)$
and
$v=(r,l,s)\in N(A)$
and
![]() $v'=(r',l',s')\in N(B)$
.
$v'=(r',l',s')\in N(B)$
.
Let
![]() $F\colon D(A)\to D(B)$
be a derived equivalence such that
$F\colon D(A)\to D(B)$
be a derived equivalence such that
![]() $F(v)=v'$
. Then, the base change of the Rouquier isomorphism to the algebraic closure
$F(v)=v'$
. Then, the base change of the Rouquier isomorphism to the algebraic closure
![]() $\bar {k}$
restricts to a group scheme isomorphism
$\bar {k}$
restricts to a group scheme isomorphism
under any of the following conditions:
-
(a) For any elements
 $\mathcal F,\mathcal G\in M_A(v)$
such that
$\mathcal F,\mathcal G\in M_A(v)$
such that
 $\operatorname {\mathrm {alb}}(\mathcal F)=\operatorname {\mathrm {alb}}(\mathcal G)$
, we have
$\operatorname {\mathrm {alb}}(\mathcal F)=\operatorname {\mathrm {alb}}(\mathcal G)$
, we have
 $\det (F(\mathcal F))=\det (F(\mathcal G))$
and
$\det (F(\mathcal F))=\det (F(\mathcal G))$
and
 $\det (\Phi _P\circ F(\mathcal F))=\det (\Phi _P\circ F(\mathcal G))$
;
$\det (\Phi _P\circ F(\mathcal F))=\det (\Phi _P\circ F(\mathcal G))$
; -
(b) F is a stability-preserving Fourier–Mukai transform; that is, if
 $E\in M_A(v)$
, then
$E\in M_A(v)$
, then
 $F(E)$
is in
$F(E)$
is in
 $M_B(v')$
; or
$M_B(v')$
; or -
(c)
 $k={\mathbb C}$
and
$k={\mathbb C}$
and
 $\frac {v^2}{2}= 3$
(i.e.,
$\frac {v^2}{2}= 3$
(i.e.,
 $K_A(v)$
is a fourfold).
$K_A(v)$
is a fourfold).
We note that the isomorphism (5.2) implies that the actions of
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
on
![]() $G_{A_{\bar {k}}}(v)$
and
$G_{A_{\bar {k}}}(v)$
and
![]() $G_{B_{\bar {k}}}(v')$
are isomorphic.
$G_{B_{\bar {k}}}(v')$
are isomorphic.
Proof. Let
![]() $(a,\alpha )\in G_{A_{\bar {k}}}(v)$
. By Remark 3.3, to prove that
$(a,\alpha )\in G_{A_{\bar {k}}}(v)$
. By Remark 3.3, to prove that
![]() $(b,\beta ):=f_{\bar {k}}(a,\alpha )\in G_{B_{\bar {k}}}(v')$
, it suffices to produce an element
$(b,\beta ):=f_{\bar {k}}(a,\alpha )\in G_{B_{\bar {k}}}(v')$
, it suffices to produce an element
![]() $\mathcal H\in D(B)$
, where
$\mathcal H\in D(B)$
, where
![]() $v(\mathcal H)=v'$
,
$v(\mathcal H)=v'$
,
![]() $\det (\mathcal H)=\det (L_{\beta }\otimes t_b^*\mathcal H)$
, and
$\det (\mathcal H)=\det (L_{\beta }\otimes t_b^*\mathcal H)$
, and
![]() $\det (\Phi _P(\mathcal H))=\det (\Phi _P(L_{\beta }\otimes t_b^*\mathcal H))$
.
$\det (\Phi _P(\mathcal H))=\det (\Phi _P(L_{\beta }\otimes t_b^*\mathcal H))$
.
Under condition (a), for any
![]() $\mathcal F\in M_A(v)$
, we may take
$\mathcal F\in M_A(v)$
, we may take
![]() $\mathcal H:=F(\mathcal F)$
. In this case, we have
$\mathcal H:=F(\mathcal F)$
. In this case, we have
![]() $L_{\beta }\otimes t_b^*\mathcal H=F(L_{\alpha }\otimes t_a^*\mathcal F)$
. Since
$L_{\beta }\otimes t_b^*\mathcal H=F(L_{\alpha }\otimes t_a^*\mathcal F)$
. Since
condition (a) allows us to conclude that
![]() $\mathcal H$
has the needed property.
$\mathcal H$
has the needed property.
Under condition (b), F restricts to an isomorphism
![]() $M_A(v)\to M_B(v')$
and by the universal property of the Albanese morphism, there is a commutative diagram as follows:
$M_A(v)\to M_B(v')$
and by the universal property of the Albanese morphism, there is a commutative diagram as follows:

Thus, F satisfies condition (a).
By [Reference Honigs21, Prop. 4.3] if
![]() $K_A(v)$
is a fourfold, the intersection of the fixed loci of
$K_A(v)$
is a fourfold, the intersection of the fixed loci of
![]() $\kappa $
and
$\kappa $
and
![]() $(L_{\alpha }\otimes t_a^*)\kappa $
acting on
$(L_{\alpha }\otimes t_a^*)\kappa $
acting on
![]() $K_A(r,l,s)$
is nonempty. For instance, in
$K_A(r,l,s)$
is nonempty. For instance, in
![]() $K_2(A)$
, the intersection of
$K_2(A)$
, the intersection of
![]() $\operatorname {\mathrm {Fix}}(\kappa )$
and
$\operatorname {\mathrm {Fix}}(\kappa )$
and
![]() $\operatorname {\mathrm {Fix}}(\kappa _{(\tau ,0)})$
where
$\operatorname {\mathrm {Fix}}(\kappa _{(\tau ,0)})$
where
![]() $\tau \in A[3]$
(cf. Lemma 3.12) contains
$\tau \in A[3]$
(cf. Lemma 3.12) contains
![]() $(0,\tau ,-\tau )$
.
$(0,\tau ,-\tau )$
.
Let
![]() $\mathcal G$
be an element in this intersection. It is thus fixed by
$\mathcal G$
be an element in this intersection. It is thus fixed by
![]() $L_{\alpha }\otimes t_a^*$
. Following the diagram above, we see that
$L_{\alpha }\otimes t_a^*$
. Following the diagram above, we see that
![]() $\mathcal H:=F(\mathcal G)$
is fixed by
$\mathcal H:=F(\mathcal G)$
is fixed by
![]() $L_{\beta }\otimes t_b^*$
and thus, F satisfies the needed condition.
$L_{\beta }\otimes t_b^*$
and thus, F satisfies the needed condition.
Remark 5.3. The barrier to a proof of Proposition 5.2 under more general conditions is that it is not known that a general Fourier–Mukai equivalence will respect the Albanese morphism acting on
![]() $M_A(v)$
.
$M_A(v)$
.
The proof of Proposition 5.2 under condition (c) hinges on the selection of an element fixed by the automorphisms from Theorem 3.1. We anticipate that analogous results are available for higher-dimensional varieties of Kummer type. For instance, in
![]() $K_{n-1}(A)$
, the intersection between
$K_{n-1}(A)$
, the intersection between
![]() $\operatorname {\mathrm {Fix}}(\iota _{(0,0)})$
and
$\operatorname {\mathrm {Fix}}(\iota _{(0,0)})$
and
![]() $\operatorname {\mathrm {Fix}}(\iota _{(\tau ,0)})$
where
$\operatorname {\mathrm {Fix}}(\iota _{(\tau ,0)})$
where
![]() $\tau \in A[n]$
contains
$\tau \in A[n]$
contains
![]() $(0,\tau ,2\tau ,\ldots ,(n-1)\tau )$
.
$(0,\tau ,2\tau ,\ldots ,(n-1)\tau )$
.
Example 5.4. (a) For any abelian surface A we have the Fourier–Mukai equivalence
![]() $\Phi _P:D(A)\to D(\hat {A})$
. For any Mukai vector v on A, condition (a) of Proposition 5.2 is satisfied for
$\Phi _P:D(A)\to D(\hat {A})$
. For any Mukai vector v on A, condition (a) of Proposition 5.2 is satisfied for
![]() $F=\Phi _P$
since
$F=\Phi _P$
since
![]() $\Phi _P\circ \Phi _P=\iota ^*\circ [-2]$
. If
$\Phi _P\circ \Phi _P=\iota ^*\circ [-2]$
. If
![]() $v:=(r,l,s)$
, then
$v:=(r,l,s)$
, then
![]() $v':=F(v)=(s,m,r)$
[Reference Yoshioka56, Lemma 3.1], and
$v':=F(v)=(s,m,r)$
[Reference Yoshioka56, Lemma 3.1], and
![]() $G_{A_{\bar {k}}}(v)$
and
$G_{A_{\bar {k}}}(v)$
and
![]() $G_{\hat {A}_{\bar {k}}}(v')$
are very closely related via the canonical identification between an abelian surface and the dual of its dual. By Theorem 3.1, the elements in
$G_{\hat {A}_{\bar {k}}}(v')$
are very closely related via the canonical identification between an abelian surface and the dual of its dual. By Theorem 3.1, the elements in
![]() $G_{A_{\bar {k}}}(v)$
satisfy the equations shown in (3.1) and the elements of
$G_{A_{\bar {k}}}(v)$
satisfy the equations shown in (3.1) and the elements of
![]() $G_{\hat {A}_{\bar {k}}}(v')$
satisfy the equations
$G_{\hat {A}_{\bar {k}}}(v')$
satisfy the equations
Thus,
![]() $(x,y)\in G_{A_{\bar {k}}}(v)$
if and only if
$(x,y)\in G_{A_{\bar {k}}}(v)$
if and only if
![]() $(-y,x)\in G_{\hat {A}_{\bar {k}}}(v')$
.
$(-y,x)\in G_{\hat {A}_{\bar {k}}}(v')$
.
(b) Let A be an abelian surface defined over a field k of characteristic
![]() $0$
with
$0$
with
![]() $\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
and
$\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
and
![]() $l^2=2n$
. By [Reference Hassett and Tschinkel20, Lem. 3.6], the Fourier–Mukai equivalence
$l^2=2n$
. By [Reference Hassett and Tschinkel20, Lem. 3.6], the Fourier–Mukai equivalence
![]() $L\otimes ^{\mathbb {L}}(-)\colon D(A) \to D(A)$
satisfies condition (a) of Proposition 5.2; in fact,
$L\otimes ^{\mathbb {L}}(-)\colon D(A) \to D(A)$
satisfies condition (a) of Proposition 5.2; in fact,
![]() $M_A(1,0,-n) \cong M_A(1,l,0)$
. Moreover, by [Reference Yoshioka56, Prop. 3.5], applying the Fourier–Mukai transform
$M_A(1,0,-n) \cong M_A(1,l,0)$
. Moreover, by [Reference Yoshioka56, Prop. 3.5], applying the Fourier–Mukai transform
![]() $\Phi _P$
followed by a shift
$\Phi _P$
followed by a shift
![]() $[-1]$
gives an isomorphism
$[-1]$
gives an isomorphism
![]() $M_{A}(1,l,0)\cong M_{\hat {A}}(0,-\hat {l},-1)$
, where
$M_{A}(1,l,0)\cong M_{\hat {A}}(0,-\hat {l},-1)$
, where
![]() $\hat {l}$
is the Néron-Severi class of
$\hat {l}$
is the Néron-Severi class of
![]() $\Phi _P(1,l,0)$
. If l is an ample generator of
$\Phi _P(1,l,0)$
. If l is an ample generator of
![]() $\operatorname {\mathrm {NS}}(A)$
, then
$\operatorname {\mathrm {NS}}(A)$
, then
![]() $-\hat {l}$
is an ample generator of
$-\hat {l}$
is an ample generator of
![]() $\operatorname {\mathrm {NS}}(\hat {A})$
.
$\operatorname {\mathrm {NS}}(\hat {A})$
.
The shift functor
![]() $[1]$
acts on Mukai vectors by multiplication by
$[1]$
acts on Mukai vectors by multiplication by
![]() $-1$
, and in general,
$-1$
, and in general,
![]() $G_A(v)=G_A(-v)$
. Thus, there are isomorphisms of group schemes
$G_A(v)=G_A(-v)$
. Thus, there are isomorphisms of group schemes
though as discussed in Remark 3.7, the groups
![]() $G_A(1,0,-n)$
and
$G_A(1,0,-n)$
and
![]() $G_{A}(1,{l},0)$
are distinct subgroups of
$G_{A}(1,{l},0)$
are distinct subgroups of
![]() $(A\times \hat {A})[n]$
.
$(A\times \hat {A})[n]$
.
5.2 Derived equivalence of fourfolds of Kummer type
The following result provides some information on Question 2 and allows us to produce an example where two such varieties over a number field k are not derived equivalent over k.
Proposition 5.5. Let A and B be isogenous abelian surfaces over a finitely generated field k of characteristic
![]() $0$
. Let v and
$0$
. Let v and
![]() $v'$
be Mukai vectors with
$v'$
be Mukai vectors with
![]() $v^2=v^{\prime 2} =6$
, so that
$v^2=v^{\prime 2} =6$
, so that
![]() $K_A(v)$
and
$K_A(v)$
and
![]() $K_B(v')$
are fourfolds. If
$K_B(v')$
are fourfolds. If
![]() $K_A(v)$
and
$K_A(v)$
and
![]() $K_B(v')$
are derived equivalent over k, then
$K_B(v')$
are derived equivalent over k, then
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
and
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
and
![]() ${\mathbb Q}_{\ell }[G_{B_{\bar {k}}}(v')]$
are isomorphic as
${\mathbb Q}_{\ell }[G_{B_{\bar {k}}}(v')]$
are isomorphic as
![]() $\operatorname {\mathrm {Gal}}(\bar {k}/k)$
-representations.
$\operatorname {\mathrm {Gal}}(\bar {k}/k)$
-representations.
We begin with a lemma about the orthogonal complement to v in the Mukai lattice.
Lemma 5.6. Let A be an abelian surface over a field k and v a Mukai vector with
![]() $v^2\geq 2$
. Let
$v^2\geq 2$
. Let
![]() $v^{\perp }\subset \tilde {H}(A_{{\bar {k}}}, {\mathbb Q}_{\ell })$
be the orthogonal complement to v under the Mukai pairing. Then, there is a Galois equivariant isomorphism
$v^{\perp }\subset \tilde {H}(A_{{\bar {k}}}, {\mathbb Q}_{\ell })$
be the orthogonal complement to v under the Mukai pairing. Then, there is a Galois equivariant isomorphism
![]() $v^{\perp } \cong H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))\oplus {\mathbb Q}_{\ell }$
.
$v^{\perp } \cong H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell }(1))\oplus {\mathbb Q}_{\ell }$
.
Proof. Let
![]() $w:=(1,0,-n)$
for
$w:=(1,0,-n)$
for
![]() $n:=\frac {v^2}{2}\geq 1$
, and note that
$n:=\frac {v^2}{2}\geq 1$
, and note that
We will show that
![]() $v^{\perp } \cong w^{\perp }$
. For any
$v^{\perp } \cong w^{\perp }$
. For any
![]() $y \in \tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
with
$y \in \tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
with
![]() $y^2\neq 0$
, let reflection through y be given by
$y^2\neq 0$
, let reflection through y be given by
Observe that
![]() $(v-w)^2\neq 0$
or
$(v-w)^2\neq 0$
or
![]() $(v+w)^2 \neq 0$
, and so reflection through
$(v+w)^2 \neq 0$
, and so reflection through
![]() $v-w$
or
$v-w$
or
![]() $v+w$
gives an isometry
$v+w$
gives an isometry
![]() $\tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell }) \xrightarrow {\sim } \tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
which sends v to
$\tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell }) \xrightarrow {\sim } \tilde {H}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
which sends v to
![]() $\pm w$
. Thus, the isometry restricts to a Galois equivariant isomorphism
$\pm w$
. Thus, the isometry restricts to a Galois equivariant isomorphism
![]() $v^{\perp } \xrightarrow {\sim } w^{\perp }$
.
$v^{\perp } \xrightarrow {\sim } w^{\perp }$
.
Lemma 5.7. Let A be an abelian surface over a field k and v a Mukai vector with
![]() $v^2\geq 6$
. Then, there is a Galois equivariant isomorphism
$v^2\geq 6$
. Then, there is a Galois equivariant isomorphism
Proof. By [Reference Yoshioka56, Thm. 0.2(2)], along with the comparison theorem for singular and étale cohomology and the smooth base change theorem, we have a Galois equivariant isomorphism
![]() $H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))\cong v^{\perp }$
(In fact, this isomorphism exists over
$H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))\cong v^{\perp }$
(In fact, this isomorphism exists over
![]() ${\mathbb Z}_{\ell }$
, while the isomorphism of Lemma 5.6 may only exist over
${\mathbb Z}_{\ell }$
, while the isomorphism of Lemma 5.6 may only exist over
![]() ${\mathbb Q}_{\ell }$
). This combined with Lemma 5.6 gives the result.
${\mathbb Q}_{\ell }$
). This combined with Lemma 5.6 gives the result.
Proof of Proposition 5.5
Suppose that
![]() $K_A(v)$
and
$K_A(v)$
and
![]() $K_B(v')$
are derived equivalent, so they have isomorphic sums of even cohomologies after Tate twists [Reference Honigs, Achter, Casalaina-Martin, Honigs and Vial22, Lem. 3.1]:
$K_B(v')$
are derived equivalent, so they have isomorphic sums of even cohomologies after Tate twists [Reference Honigs, Achter, Casalaina-Martin, Honigs and Vial22, Lem. 3.1]:
![]() $\widetilde {H}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell })\cong \widetilde {H}(K_B(v')_{\bar {k}},{\mathbb Q}_{\ell })$
. We know that the zeroth and top cohomologies of
$\widetilde {H}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell })\cong \widetilde {H}(K_B(v')_{\bar {k}},{\mathbb Q}_{\ell })$
. We know that the zeroth and top cohomologies of
![]() $K_A(v)$
and
$K_A(v)$
and
![]() $K_B(v')$
are trivial Galois representations, and Lemma 5.7 gives that
$K_B(v')$
are trivial Galois representations, and Lemma 5.7 gives that
By Theorem 4.4 and Poincáre duality (cf. [Reference Hosono, Lian, Oguiso and Yau23]), it follows that there is an isomorphism of Galois modules
where
![]() $V_A:=V$
from Theorem 4.4. There is a similar isomorphism for
$V_A:=V$
from Theorem 4.4. There is a similar isomorphism for
![]() $\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
involving
$\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
involving
![]() $V_B$
. We will check that these representations are semisimple, so that we can reduce to a comparison of
$V_B$
. We will check that these representations are semisimple, so that we can reduce to a comparison of
![]() $V_A$
and
$V_A$
and
![]() $V_B$
.
$V_B$
.
By [Reference Fogarty13, Thm. 3] and its extension to finitely generated fields of characteristic 0 in [Reference Zarhin57, Thm. 4.3],
![]() $H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
is a semisimple representation, and thus so is
$H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}}, {\mathbb Q}_{\ell })$
is a semisimple representation, and thus so is
![]() $\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
. The
$\operatorname {\mathrm {Sym}}^2H^2_{\mathrm {\acute{e}t}}(K_A(v)_{\bar {k}},{\mathbb Q}_{\ell }(1))$
. The
![]() $\operatorname {\mathrm {Gal}}({\bar {k}}/k)$
-representation
$\operatorname {\mathrm {Gal}}({\bar {k}}/k)$
-representation
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
factors through a finite group representation, determined by the finite extension of k over which
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)]$
factors through a finite group representation, determined by the finite extension of k over which
![]() $G_{A_{\bar {k}}}(v)$
is defined, and so by Maschke’s theorem, it is also semisimple. Thus, the representation
$G_{A_{\bar {k}}}(v)$
is defined, and so by Maschke’s theorem, it is also semisimple. Thus, the representation
![]() $\widetilde {H}(K_A(v),{\mathbb Q}_{\ell })$
is semisimple. The same also holds for
$\widetilde {H}(K_A(v),{\mathbb Q}_{\ell })$
is semisimple. The same also holds for
![]() $\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
, so applying Schur’s Lemma, this allows us to cancel isomorphic representations in the direct sums for
$\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
, so applying Schur’s Lemma, this allows us to cancel isomorphic representations in the direct sums for
![]() $\widetilde {H}(K_A(v),{\mathbb Q}_{\ell })$
and for
$\widetilde {H}(K_A(v),{\mathbb Q}_{\ell })$
and for
![]() $\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
. Since A and B are isogenous, there is an isomorphism
$\widetilde {H}(K_B(v'),{\mathbb Q}_{\ell })$
. Since A and B are isogenous, there is an isomorphism
![]() $H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell })\cong H^2_{\mathrm {\acute{e}t}}(B_{\bar {k}},{\mathbb Q}_{\ell })$
, so along with the observations above, we are reduced to an isomorphism
$H^2_{\mathrm {\acute{e}t}}(A_{\bar {k}},{\mathbb Q}_{\ell })\cong H^2_{\mathrm {\acute{e}t}}(B_{\bar {k}},{\mathbb Q}_{\ell })$
, so along with the observations above, we are reduced to an isomorphism
![]() $V_A\cong V_B$
. This extends to an isomorphism
$V_A\cong V_B$
. This extends to an isomorphism
![]() ${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)] \cong {\mathbb Q}_{\ell }[G_{B_{\bar {k}}}(v')]$
, as desired.
${\mathbb Q}_{\ell }[G_{A_{\bar {k}}}(v)] \cong {\mathbb Q}_{\ell }[G_{B_{\bar {k}}}(v')]$
, as desired.
We use this result to give a negative answer to Question 2 in the case of generalized Kummer varieties
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
.
$K_2(\hat {A})$
.
Corollary 5.8. For an abelian surface A defined over a number field k for which
![]() ${\mathbb Q}_{\ell }[A[3]]$
and
${\mathbb Q}_{\ell }[A[3]]$
and
![]() ${\mathbb Q}_{\ell }[\hat {A}[3]]$
are not isomorphic as Galois modules over k,
${\mathbb Q}_{\ell }[\hat {A}[3]]$
are not isomorphic as Galois modules over k,
![]() $K_2(A)\cong K_A(1,0,-3)$
and
$K_2(A)\cong K_A(1,0,-3)$
and
![]() $K_2(\hat {A})\cong K_A(3,0,-1)$
are not derived equivalent over k.
$K_2(\hat {A})\cong K_A(3,0,-1)$
are not derived equivalent over k.
Proof. We have
![]() $G_{A_{\bar {k}}}(1,0,-3)=A[3]$
and by the discussion in Example 5.4(a),
$G_{A_{\bar {k}}}(1,0,-3)=A[3]$
and by the discussion in Example 5.4(a),
![]() $G_{A_{\bar {k}}}(3,0,-1)=G_{\hat {A}_{\bar {k}}}(1,0,-3)=\hat {A}[3]$
. The result then follows by Proposition 5.5.
$G_{A_{\bar {k}}}(3,0,-1)=G_{\hat {A}_{\bar {k}}}(1,0,-3)=\hat {A}[3]$
. The result then follows by Proposition 5.5.
In [Reference Fu and Li16] the authors exhibit an abelian surface A defined over a number field k where
![]() ${\mathbb Q}_{\ell }[A[3]]$
and
${\mathbb Q}_{\ell }[A[3]]$
and
![]() ${\mathbb Q}_{\ell }[\hat {A}[3]]$
are not isomorphic as Galois modules over k.
${\mathbb Q}_{\ell }[\hat {A}[3]]$
are not isomorphic as Galois modules over k.
Remark 5.9. If A is an abelian surface as in the proof of Corollary 5.8, any derived equivalence between
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
would have to be defined over a field larger than k. Moreover, the kernel of such a derived equivalence could not be constructed out of only universal bundles, since such bundles would naturally be defined over k, and the derived equivalence would descend.
$K_2(\hat {A})$
would have to be defined over a field larger than k. Moreover, the kernel of such a derived equivalence could not be constructed out of only universal bundles, since such bundles would naturally be defined over k, and the derived equivalence would descend.
Remark 5.10. The argument in Corollary 5.8 cannot be used to rule out derived equivalences between
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
in many contexts; for instance, it does not work when A is principally polarized, since such a polarization would give an isomorphism between
$K_2(\hat {A})$
in many contexts; for instance, it does not work when A is principally polarized, since such a polarization would give an isomorphism between
![]() $A[3]$
and
$A[3]$
and
![]() $\hat {A}[3]$
.
$\hat {A}[3]$
.
Proposition 5.5 also holds for Kummer varieties over fields of positive characteristic that satisfy the hypotheses of Proposition 4.6; Tate’s theorem gives the needed semisimplicity result [Reference Tate55]. However, over a finite field in general, Tate’s isogeny theorem implies there is an isomorphism between the Tate modules
![]() $T_{\ell }A$
and
$T_{\ell }A$
and
![]() $T_{\ell }\hat {A}$
. Thus, it would not be possible to use the approach of Corollary 5.8 to rule out a derived equivalence between
$T_{\ell }\hat {A}$
. Thus, it would not be possible to use the approach of Corollary 5.8 to rule out a derived equivalence between
![]() $K_2(A)$
and
$K_2(A)$
and
![]() $K_2(\hat {A})$
if A was defined over a finite field.
$K_2(\hat {A})$
if A was defined over a finite field.
6 A
 $(1,3)$
-polarized example: Lagrangian fibrations
$(1,3)$
-polarized example: Lagrangian fibrations
In this and the following sections, we consider an extended example where we work over
![]() ${\mathbb C}$
.
${\mathbb C}$
.
Let
![]() $(A,L)$
be a polarized abelian surface where L is symmetric,
$(A,L)$
be a polarized abelian surface where L is symmetric,
![]() $\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
for
$\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
for
![]() $l:=c_1(L)$
and
$l:=c_1(L)$
and
![]() $l^2=6$
, so L is a
$l^2=6$
, so L is a
![]() $(1,3)$
-polarization (see Claim 3.4). Let
$(1,3)$
-polarization (see Claim 3.4). Let
![]() $K_A(0,l,s)$
be as in Setting 2.4 and assume
$K_A(0,l,s)$
be as in Setting 2.4 and assume
![]() $M\in \operatorname {\mathrm {Pic}}^{m}(\hat {A})$
is also symmetric. We will see below that the spaces
$M\in \operatorname {\mathrm {Pic}}^{m}(\hat {A})$
is also symmetric. We will see below that the spaces
![]() $K_A(0,l,s)$
are fibered over
$K_A(0,l,s)$
are fibered over
![]() ${\mathbb P}^2$
in Jacobians of irreducible genus 4 curves, and while they can be identified fiberwise as s varies, their global geometry differs: the discriminant of the Beauville–Bogomolov–Fujiki form on
${\mathbb P}^2$
in Jacobians of irreducible genus 4 curves, and while they can be identified fiberwise as s varies, their global geometry differs: the discriminant of the Beauville–Bogomolov–Fujiki form on
![]() $\operatorname {\mathrm {Pic}}(K_A(0,l,s))$
changes, so these moduli spaces are not, in general, birational.
$\operatorname {\mathrm {Pic}}(K_A(0,l,s))$
changes, so these moduli spaces are not, in general, birational.
We consider the fixed locus of
![]() $K_A(0,l,s)$
under the action of
$K_A(0,l,s)$
under the action of
![]() $\iota ^*$
, which we refer to as
$\iota ^*$
, which we refer to as
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
. By Lemma 3.12, the fixed locus of any symplectic involution on
$\operatorname {\mathrm {Fix}}(\iota ^*)$
. By Lemma 3.12, the fixed locus of any symplectic involution on
![]() $K_A(0,l,s)$
is a translation of
$K_A(0,l,s)$
is a translation of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
. The moduli space
$\operatorname {\mathrm {Fix}}(\iota ^*)$
. The moduli space
![]() $K_A(0,l,s)$
parametrizes rank
$K_A(0,l,s)$
parametrizes rank
![]() $1$
stable sheaves, or equivalently, rank
$1$
stable sheaves, or equivalently, rank
![]() $1$
torsion-free sheaves, supported on irreducible curves in A. When the supporting curves are smooth, these sheaves are line bundles on the curves, but we also encounter curves with nodal singularities, in which case the space of rank 1 torsion-free sheaves naturally compactifies the space of line bundles.
$1$
torsion-free sheaves, supported on irreducible curves in A. When the supporting curves are smooth, these sheaves are line bundles on the curves, but we also encounter curves with nodal singularities, in which case the space of rank 1 torsion-free sheaves naturally compactifies the space of line bundles.
In this section, we give necessary background and show that there is a natural fibration of
![]() $K_A(0,l,s)$
in abelian surfaces such that
$K_A(0,l,s)$
in abelian surfaces such that
![]() $\operatorname {\mathrm {Fix}}({\iota ^*})\subset K_A(0,l,s)$
contains an elliptically fibered K3 surface. In Section 7, we will analyze the singular fibers of this K3 surface, and in Section 8 we will analyze the isolated points of the fixed locus.
$\operatorname {\mathrm {Fix}}({\iota ^*})\subset K_A(0,l,s)$
contains an elliptically fibered K3 surface. In Section 7, we will analyze the singular fibers of this K3 surface, and in Section 8 we will analyze the isolated points of the fixed locus.
For comparison, we first give a description of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
in
$\operatorname {\mathrm {Fix}}(\iota ^*)$
in
![]() $K_A(1,0,-3)$
here.
$K_A(1,0,-3)$
here.
6.1
 $\operatorname {\mathrm {Fix}}(\iota ^*)$
for
$\operatorname {\mathrm {Fix}}(\iota ^*)$
for
 $K_2(A)$
$K_2(A)$
The points in
![]() $K_2(A)\cong K_A(1,0,-3)$
consist of
$K_2(A)\cong K_A(1,0,-3)$
consist of
![]() $0$
-dimensional length
$0$
-dimensional length
![]() $3$
subschemes of A for which the support sums to
$3$
subschemes of A for which the support sums to
![]() $0$
. It was shown in [Reference Honigs21, Thm. 4.4] that
$0$
. It was shown in [Reference Honigs21, Thm. 4.4] that
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
contains the Kummer K3 surface
$\operatorname {\mathrm {Fix}}(\iota ^*)$
contains the Kummer K3 surface
as well as a unique isolated point supported at the identity element
![]() $0$
.
$0$
.
Any length
![]() $3$
subscheme in
$3$
subscheme in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
containing a point
$\operatorname {\mathrm {Fix}}(\iota ^*)$
containing a point
![]() $a\in A$
in its support that is not fixed by
$a\in A$
in its support that is not fixed by
![]() $\iota ^*$
must be of the form
$\iota ^*$
must be of the form
![]() $(0,a,-a)$
, which is in the Kummer K3 surface described above. Thus, the remaining isolated points in
$(0,a,-a)$
, which is in the Kummer K3 surface described above. Thus, the remaining isolated points in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
found by Tarí [Reference Tarí54] must consist of triples of three distinct points of
$\operatorname {\mathrm {Fix}}(\iota ^*)$
found by Tarí [Reference Tarí54] must consist of triples of three distinct points of
![]() $A[2]\cong ({\mathbb Z}/2{\mathbb Z})^4$
that sum to
$A[2]\cong ({\mathbb Z}/2{\mathbb Z})^4$
that sum to
![]() $0$
. The identity element cannot be contained in such a triple. Once we have chosen two of the points, the third is forced, and length
$0$
. The identity element cannot be contained in such a triple. Once we have chosen two of the points, the third is forced, and length
![]() $3$
subschemes are unordered, so we have
$3$
subschemes are unordered, so we have
such isolated points.
6.2 Stable sheaves and compactifications of the Jacobian
Let
![]() $\operatorname {\mathrm {Pic}}^d(C)$
be the set of degree d line bundles on any curve C. We write
$\operatorname {\mathrm {Pic}}^d(C)$
be the set of degree d line bundles on any curve C. We write
![]() $\operatorname {\mathrm {Pic}}^d_C$
for the Picard scheme of degree d on a curve C, and we use
$\operatorname {\mathrm {Pic}}^d_C$
for the Picard scheme of degree d on a curve C, and we use
![]() $\overline {\mathrm {Pic}}{}^d_C$
to denote the moduli scheme parametrizing rank
$\overline {\mathrm {Pic}}{}^d_C$
to denote the moduli scheme parametrizing rank
![]() $1$
degree d torsion-free sheaves on the mildly singular curves C that arise in this paper, which are all Gorenstein and, moreover, have planar singularities.
$1$
degree d torsion-free sheaves on the mildly singular curves C that arise in this paper, which are all Gorenstein and, moreover, have planar singularities.
If C is elliptic,
![]() $\operatorname {\mathrm {Pic}}^d_C\cong C$
for any d, and this fact has some generalizations to compactified Jacobians of singular genus
$\operatorname {\mathrm {Pic}}^d_C\cong C$
for any d, and this fact has some generalizations to compactified Jacobians of singular genus
![]() $1$
curves that we will find useful.
$1$
curves that we will find useful.
Proposition 6.1 [Reference Langer33, §3, p. 14],[Reference Faltings12, Ex. 39]
Let C be a genus
![]() $1$
reduced curve that is irreducible and nodal. Then,
$1$
reduced curve that is irreducible and nodal. Then,
![]() $\overline {\mathrm {Pic}}{}^d_C\cong C$
for any d.
$\overline {\mathrm {Pic}}{}^d_C\cong C$
for any d.
The Abel map [Reference Langer33, Def. 1.0.5] and a generalization of it for compactified Jacobians of Gorenstein curves is useful to our arguments. We use the development of this map given by Kass in [Reference Langer33], though we do not need the full power of Kass’s theory.
Generalized divisors on C are nonzero subsheaves of the sheaf of the total quotient ring of C,
![]() $I_D\subset \mathcal {K}$
, that are coherent
$I_D\subset \mathcal {K}$
, that are coherent
![]() $\mathcal O_C$
-modules. These divisors generalize Cartier divisors, which they coincide with when
$\mathcal O_C$
-modules. These divisors generalize Cartier divisors, which they coincide with when
![]() $I_D$
is a line bundle. An effective generalized divisor on C is a
$I_D$
is a line bundle. An effective generalized divisor on C is a
![]() $0$
-dimensional closed subscheme
$0$
-dimensional closed subscheme
![]() $Z\subset C$
, meaning the following generalization of the Abel map continues to have the intuitive quality of sending points to corresponding elements in
$Z\subset C$
, meaning the following generalization of the Abel map continues to have the intuitive quality of sending points to corresponding elements in
![]() $\overline {\mathrm {Pic}}{}^{-d}_C$
[Reference Langer33, Def. 5.0.7], [Reference Altman and Kleiman2, Thm. 8.5]:
$\overline {\mathrm {Pic}}{}^{-d}_C$
[Reference Langer33, Def. 5.0.7], [Reference Altman and Kleiman2, Thm. 8.5]:
 $$ \begin{align} \alpha\colon \operatorname{\mathrm{Hilb}}^d_C &\to \overline{\mathrm{Pic}}{}^{-d}_C\\ [D] &\mapsto I_D\notag \end{align} $$
$$ \begin{align} \alpha\colon \operatorname{\mathrm{Hilb}}^d_C &\to \overline{\mathrm{Pic}}{}^{-d}_C\\ [D] &\mapsto I_D\notag \end{align} $$
When the degree d is greater than or equal to the arithmetic genus g, this map is surjective and generically has fibers isomorphic to
![]() ${\mathbb P}^{d-g}$
. If D is an effective generalized divisor,
${\mathbb P}^{d-g}$
. If D is an effective generalized divisor,
![]() $\alpha ^{-1}([I_D])$
is the complete linear system
$\alpha ^{-1}([I_D])$
is the complete linear system
![]() $|D|$
. If
$|D|$
. If
![]() $g=d$
, the map is generically injective. The locus where
$g=d$
, the map is generically injective. The locus where
![]() $\alpha $
is non-injective in this case is the exceptional locus
$\alpha $
is non-injective in this case is the exceptional locus
![]() $C^1_d$
, which consists of divisors D whose image under the canonical map lies on a hyperplane. Such divisors
$C^1_d$
, which consists of divisors D whose image under the canonical map lies on a hyperplane. Such divisors
![]() $D,D'$
are linearly equivalent if there are canonical divisors
$D,D'$
are linearly equivalent if there are canonical divisors
![]() $K,K'$
such that
$K,K'$
such that
![]() $K-D=K'-D'$
.
$K-D=K'-D'$
.
Related to Proposition 6.1, this generalized Abel map is an isomorphism when C is a nodal genus-
![]() $1$
curve.
$1$
curve.
6.3 The Lagrangian fibration of
 $K_A(0,l,s)$
$K_A(0,l,s)$
Since
![]() $l^2=6$
,
$l^2=6$
,
![]() $K_A(0,l,s)$
is
$K_A(0,l,s)$
is
![]() $4$
-dimensional, and since
$4$
-dimensional, and since
![]() $\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
for
$\operatorname {\mathrm {NS}}(A)={\mathbb Z} l$
for
![]() $l:=c_1(L)$
, the curves
$l:=c_1(L)$
, the curves
![]() $C\in |L|$
are irreducible. Hence, all rank 1 torsion-free sheaves are stable. Thus,
$C\in |L|$
are irreducible. Hence, all rank 1 torsion-free sheaves are stable. Thus,
![]() $K_A(0,l,s)$
parametrizes rank 1 torsion-free sheaves on irreducible curves
$K_A(0,l,s)$
parametrizes rank 1 torsion-free sheaves on irreducible curves
![]() $C\subset A$
where
$C\subset A$
where
![]() $C\in |L|$
, which are generically line bundles. Curves in this linear system have arithmetic genus
$C\in |L|$
, which are generically line bundles. Curves in this linear system have arithmetic genus
![]() $4$
and by Riemann-Roch, the line bundles parametrized by
$4$
and by Riemann-Roch, the line bundles parametrized by
![]() $K_A(0,l,s)$
have degree
$K_A(0,l,s)$
have degree
![]() $d:=s+3$
.
$d:=s+3$
.
We see that
![]() $h^0(A,L)=3$
and
$h^0(A,L)=3$
and
![]() $h^1(A,L)=h^2(A,L)=0$
. Thus, there is a map sending elements of
$h^1(A,L)=h^2(A,L)=0$
. Thus, there is a map sending elements of
![]() $K_A(0,l,s)$
to their supports in the linear system
$K_A(0,l,s)$
to their supports in the linear system
![]() $|L|$
:
$|L|$
:
 $$ \begin{align} f\colon K_A(0,l,s)&\to {\mathbb P}^2\cong |L|\\ \mathcal F&\mapsto \operatorname{\mathrm{supp}}(\mathcal F) \notag \end{align} $$
$$ \begin{align} f\colon K_A(0,l,s)&\to {\mathbb P}^2\cong |L|\\ \mathcal F&\mapsto \operatorname{\mathrm{supp}}(\mathcal F) \notag \end{align} $$
Lemma 6.2. Let
![]() $C\in |L|$
and
$C\in |L|$
and
![]() $h_C\colon C\hookrightarrow A$
be the natural inclusion. The fiber of f over
$h_C\colon C\hookrightarrow A$
be the natural inclusion. The fiber of f over
![]() $C\in |L|$
is the fiber over M of the following surjective morphism:
$C\in |L|$
is the fiber over M of the following surjective morphism:
 $$ \begin{align} \varphi_C\colon \overline{\mathrm{Pic}}{}_C^d &\to \operatorname{\mathrm{Pic}}^{m}_{\hat{A}}\\ \mathcal F &\mapsto \det(\Phi_P(h_{C*}\mathcal F)).\notag \end{align} $$
$$ \begin{align} \varphi_C\colon \overline{\mathrm{Pic}}{}_C^d &\to \operatorname{\mathrm{Pic}}^{m}_{\hat{A}}\\ \mathcal F &\mapsto \det(\Phi_P(h_{C*}\mathcal F)).\notag \end{align} $$
This fiber
![]() $f^{-1}(C)=\varphi _C^{-1}(M)$
is a translation of the fiber of the following map over
$f^{-1}(C)=\varphi _C^{-1}(M)$
is a translation of the fiber of the following map over
![]() $0_A$
:
$0_A$
:
 $$ \begin{align} j_C:\overline{\mathrm{Pic}}{}^0_C\to A\\ I_D\to -\Sigma D,\notag \end{align} $$
$$ \begin{align} j_C:\overline{\mathrm{Pic}}{}^0_C\to A\\ I_D\to -\Sigma D,\notag \end{align} $$
where
![]() $\Sigma D$
is the sum of points in the divisor D using the group law on A.
$\Sigma D$
is the sum of points in the divisor D using the group law on A.
When C is smooth,
![]() $j_C$
is the morphism given by the universal property of the Jacobian, which sends a line bundle (e.g.,
$j_C$
is the morphism given by the universal property of the Jacobian, which sends a line bundle (e.g.,
![]() ${\mathcal O}(p-q)$
) to
${\mathcal O}(p-q)$
) to
![]() $p-q$
.
$p-q$
.
Remark 6.3. We will analyze the
![]() $\iota ^*$
-invariant portion of
$\iota ^*$
-invariant portion of
![]() $\varphi _C^{-1}(M)$
in later results. This lemma shows that we may reduce to analyzing the
$\varphi _C^{-1}(M)$
in later results. This lemma shows that we may reduce to analyzing the
![]() $\iota ^*$
-invariant portion of the fiber of
$\iota ^*$
-invariant portion of the fiber of
![]() $j_C$
over
$j_C$
over
![]() $0_A$
, which we call
$0_A$
, which we call
![]() $\ker j_C$
, somewhat abusing notation in the singular case.
$\ker j_C$
, somewhat abusing notation in the singular case.
Proof. Recall that
![]() $K_A(0,l,s)$
is the fiber of the Albanese map over
$K_A(0,l,s)$
is the fiber of the Albanese map over
![]() $(L,M)$
:
$(L,M)$
:
We consider the interaction of
![]() $\operatorname {\mathrm {alb}}$
with f. Let
$\operatorname {\mathrm {alb}}$
with f. Let
![]() $\mathcal C$
be the tautological family of curves in
$\mathcal C$
be the tautological family of curves in
![]() $|L|$
. We may identify the fiber of (6.6) over
$|L|$
. We may identify the fiber of (6.6) over
![]() $\{L\}\times \operatorname {\mathrm {Pic}}^{m}_{\hat {A}}$
with the relative compactified Jacobian
$\{L\}\times \operatorname {\mathrm {Pic}}^{m}_{\hat {A}}$
with the relative compactified Jacobian
![]() $\smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}$
, which has a map to supports
$\smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}$
, which has a map to supports
![]() $g:\smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}\to |L|$
. Thus, there is an inclusion
$g:\smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}\to |L|$
. Thus, there is an inclusion
![]() $K_A(0,l,s) \hookrightarrow \smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}$
making the following diagram commute:
$K_A(0,l,s) \hookrightarrow \smash {\overline {\mathrm {Pic}}{}^d_{\mathcal C/{\mathbb P}^2}}$
making the following diagram commute:

For any curve
![]() $C\in |L|$
, the fiber of g over C is
$C\in |L|$
, the fiber of g over C is
![]() $\overline {\mathrm {Pic}}{}^d_C$
, which is isomorphic to
$\overline {\mathrm {Pic}}{}^d_C$
, which is isomorphic to
![]() $\operatorname {\mathrm {Pic}}^d_C$
if C is smooth. The morphism
$\operatorname {\mathrm {Pic}}^d_C$
if C is smooth. The morphism
![]() $\varphi _C$
given in the statement of the lemma is the restriction of the Albanese morphism (6.6) on
$\varphi _C$
given in the statement of the lemma is the restriction of the Albanese morphism (6.6) on
![]() $M_A(0,l,s)$
to
$M_A(0,l,s)$
to
![]() $\overline {\mathrm {Pic}}{}^d_C$
. Using (6.7), we see the fiber of f over C is equal to the fiber of
$\overline {\mathrm {Pic}}{}^d_C$
. Using (6.7), we see the fiber of f over C is equal to the fiber of
![]() $\varphi _C$
over M.
$\varphi _C$
over M.
Let
![]() $\mathcal L$
be a line bundle on C and p a point in C. As in [Reference Artin, Grothendieck and Verdier52, §17.2], applying
$\mathcal L$
be a line bundle on C and p a point in C. As in [Reference Artin, Grothendieck and Verdier52, §17.2], applying
![]() $\det (\Phi _P(h_{C*}-))$
to the short exact sequence
$\det (\Phi _P(h_{C*}-))$
to the short exact sequence
implies
where
![]() $P_p$
is the line bundle on
$P_p$
is the line bundle on
![]() $\hat {A}$
corresponding to
$\hat {A}$
corresponding to
![]() $p\in C\subset A$
. Moreover, for any divisor D on C, we have
$p\in C\subset A$
. Moreover, for any divisor D on C, we have
where
![]() $P_{\Sigma D}$
is the line bundle on
$P_{\Sigma D}$
is the line bundle on
![]() $\hat {A}$
corresponding to the point on A that comes from summing D using the group law on A. If C is singular, this argument may be extended to ideal sheaves of generalized divisors D. Thus,
$\hat {A}$
corresponding to the point on A that comes from summing D using the group law on A. If C is singular, this argument may be extended to ideal sheaves of generalized divisors D. Thus,
![]() $\varphi _C$
is a translation of the morphism
$\varphi _C$
is a translation of the morphism
![]() $j_C$
of (6.5) by an element of
$j_C$
of (6.5) by an element of
![]() $\overline {\mathrm {Pic}}{}^d(C)$
.
$\overline {\mathrm {Pic}}{}^d(C)$
.
If C is smooth, the map induced by applying the universal property of the Jacobian to the inclusion
![]() $C\hookrightarrow A$
is surjective [Reference Donovan10]; thus,
$C\hookrightarrow A$
is surjective [Reference Donovan10]; thus,
![]() $\varphi _C$
is surjective as well.
$\varphi _C$
is surjective as well.
Alternately, to prove
![]() $\varphi _C$
is surjective for smooth curves C, we may observe that
$\varphi _C$
is surjective for smooth curves C, we may observe that
![]() $\varphi _C$
is equivariant under the action of
$\varphi _C$
is equivariant under the action of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
and the action of
$\operatorname {\mathrm {Pic}}^0(A)$
and the action of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
on
$\operatorname {\mathrm {Pic}}^0(A)$
on
![]() $\operatorname {\mathrm {Pic}}^{m}\hat {A}$
is transitive. For singular C, if we restrict
$\operatorname {\mathrm {Pic}}^{m}\hat {A}$
is transitive. For singular C, if we restrict
![]() $\varphi _C$
to
$\varphi _C$
to
![]() $\operatorname {\mathrm {Pic}}^d_C\subset \overline {\mathrm {Pic}}{}^d_C$
, the same argument holds and so
$\operatorname {\mathrm {Pic}}^d_C\subset \overline {\mathrm {Pic}}{}^d_C$
, the same argument holds and so
![]() $\varphi _C$
is surjective.
$\varphi _C$
is surjective.
In [Reference Hassett and Tschinkel20], Gulbrandsen shows that the map
![]() $f\colon K_A(0,l,-1)\to {\mathbb P}^2$
is a Lagrangian fibration. There is a similar Lagrangian fibration of
$f\colon K_A(0,l,-1)\to {\mathbb P}^2$
is a Lagrangian fibration. There is a similar Lagrangian fibration of
![]() $K_A(0,l,s)$
for any choice of s.
$K_A(0,l,s)$
for any choice of s.
Proposition 6.4. For any s, the map
![]() $f\colon K(0,l,s)\to {\mathbb P}^2$
is a Lagrangian fibration.
$f\colon K(0,l,s)\to {\mathbb P}^2$
is a Lagrangian fibration.
Proof. By [Reference Milne39, Thm. 1], it suffices to prove that f is surjective and its fibers are connected. By Lemma 6.2, the fiber of f over
![]() $C\in |L|$
is the fiber of
$C\in |L|$
is the fiber of
![]() $\varphi _C$
over M, which is nonempty since
$\varphi _C$
over M, which is nonempty since
![]() $\varphi _C$
is surjective. Thus, f is surjective. By [Reference Donovan10, Lem. 2.6], the fibers of f over smooth curves are connected. By considering the Stein factorization of f, we conclude that f has connected fibers.
$\varphi _C$
is surjective. Thus, f is surjective. By [Reference Donovan10, Lem. 2.6], the fibers of f over smooth curves are connected. By considering the Stein factorization of f, we conclude that f has connected fibers.
6.4 The Lagrangian fibration restricted to
 $\operatorname {\mathrm {Fix}}(\iota ^*)$
$\operatorname {\mathrm {Fix}}(\iota ^*)$
Since
![]() $K(0,l,s)$
is fibered over
$K(0,l,s)$
is fibered over
![]() $|L|$
, we begin by analyzing the action of
$|L|$
, we begin by analyzing the action of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $|L|$
.
$|L|$
.
The restriction of the Weil pairing
![]() $\langle -,\phi _L(-)\rangle $
on points in A to
$\langle -,\phi _L(-)\rangle $
on points in A to
![]() $A[2]$
yields a quadratic form
$A[2]$
yields a quadratic form
![]() $q_L\colon A[2]\to \mu _2$
. Since
$q_L\colon A[2]\to \mu _2$
. Since
![]() $\ker (\phi _L)\cong ({\mathbb Z}/3{\mathbb Z})^2$
(see Claim 3.4), it contains only the trivial element of
$\ker (\phi _L)\cong ({\mathbb Z}/3{\mathbb Z})^2$
(see Claim 3.4), it contains only the trivial element of
![]() $A[2]$
. Hence,
$A[2]$
. Hence,
![]() $q_L$
is nondegenerate. Whether
$q_L$
is nondegenerate. Whether
![]() $q_L$
is even or odd as a quadratic form (cf. [Reference Artin, Grothendieck and Verdier52, p. 63], [Reference Borówka and Sankaran9, §3]) determines several facts about the action of
$q_L$
is even or odd as a quadratic form (cf. [Reference Artin, Grothendieck and Verdier52, p. 63], [Reference Borówka and Sankaran9, §3]) determines several facts about the action of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $|L|$
.
$|L|$
.
Proposition 6.5. The action of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $H^0(A,L)$
decomposes into eigenspaces
$H^0(A,L)$
decomposes into eigenspaces
![]() $H^0(A,L)_+$
and
$H^0(A,L)_+$
and
![]() $H^0(A,L)_-$
with eigenvalues
$H^0(A,L)_-$
with eigenvalues
![]() $\pm 1$
. Furthermore,
$\pm 1$
. Furthermore,
 $$\begin{align*}\dim(H^0(A,L)_+)= \begin{cases} 2 & \text{if } q_L \text{ is even} \\ 1 & \text{if } q_L \text{ is odd} \end{cases} \quad \dim(H^0(A,L)_-)= \begin{cases} 1 & \text{if } q_L \text{ is even} \\ 2 & \text{if } q_L \text{ is odd}. \end{cases} \end{align*}$$
$$\begin{align*}\dim(H^0(A,L)_+)= \begin{cases} 2 & \text{if } q_L \text{ is even} \\ 1 & \text{if } q_L \text{ is odd} \end{cases} \quad \dim(H^0(A,L)_-)= \begin{cases} 1 & \text{if } q_L \text{ is even} \\ 2 & \text{if } q_L \text{ is odd}. \end{cases} \end{align*}$$
We call the
![]() $1$
-dimensional and
$1$
-dimensional and
![]() $2$
-dimensional eigenspaces, respectively,
$2$
-dimensional eigenspaces, respectively,
For generic A, any curve
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
is smooth and hyperelliptic, and there are
$C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
is smooth and hyperelliptic, and there are
![]() $10$
points in
$10$
points in
![]() $A[2]$
though which it passes. If
$A[2]$
though which it passes. If
![]() $q_L$
is even, then
$q_L$
is even, then
![]() $0_A$
is among these
$0_A$
is among these
![]() $10$
points. The remaining
$10$
points. The remaining
![]() $6$
points in
$6$
points in
![]() $A[2]$
are the base locus of
$A[2]$
are the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. If
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. If
![]() $q_L$
is odd, then
$q_L$
is odd, then
![]() $0_A$
is among these
$0_A$
is among these
![]() $6$
points.
$6$
points.
The space
![]() $V_{\operatorname {\mathrm {hyp}}}$
was named for the fact that the curves in it are hyperelliptic. The name
$V_{\operatorname {\mathrm {hyp}}}$
was named for the fact that the curves in it are hyperelliptic. The name
![]() $V_{\operatorname {\mathrm {ell}}}$
was chosen because, by Riemann–Hurwitz, quotients
$V_{\operatorname {\mathrm {ell}}}$
was chosen because, by Riemann–Hurwitz, quotients
![]() $C/\iota $
of smooth curves
$C/\iota $
of smooth curves
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
are elliptic.
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
are elliptic.
Proof. Calculations on the dimensions of
![]() $H^0(A,L)_{\pm }$
and the number of points through which these curves pass have been carried out in [Reference Borówka and Sankaran9, §3], [Reference Donovan10, §3] and [Reference O’Grady48]. See [Reference Boissière, Nieper-Wißkirchen and Sarti7, Ch. 4] and [Reference Artin, Grothendieck and Verdier52, Ch. 13] for further details.
$H^0(A,L)_{\pm }$
and the number of points through which these curves pass have been carried out in [Reference Borówka and Sankaran9, §3], [Reference Donovan10, §3] and [Reference O’Grady48]. See [Reference Boissière, Nieper-Wißkirchen and Sarti7, Ch. 4] and [Reference Artin, Grothendieck and Verdier52, Ch. 13] for further details.
By Proposition 4.1,
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
consists of a K3 surface and
$\operatorname {\mathrm {Fix}}(\iota ^*)$
consists of a K3 surface and
![]() $36$
isolated points. Here, we study the geometry of the K3 surface.
$36$
isolated points. Here, we study the geometry of the K3 surface.
Proposition 6.6. The K3 surface in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
is elliptically fibered.
$\operatorname {\mathrm {Fix}}(\iota ^*)$
is elliptically fibered.
Proof. By Proposition 6.5,
and thus,
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
is fibered over
$\operatorname {\mathrm {Fix}}(\iota ^*)$
is fibered over
![]() ${\mathbb P}^1\sqcup {\mathbb P}^0$
.
${\mathbb P}^1\sqcup {\mathbb P}^0$
.
By Lemma 6.2, the fiber of
![]() $K_A(0,l,s)$
over C is the fiber of
$K_A(0,l,s)$
over C is the fiber of
![]() $\varphi _C$
over M. Let
$\varphi _C$
over M. Let
![]() $C\in |L|^{\iota ^*}$
be smooth. By Remark 6.3, to determine the dimension of the
$C\in |L|^{\iota ^*}$
be smooth. By Remark 6.3, to determine the dimension of the
![]() $\iota ^*$
-invariant parts of this fiber, we examine the eigenvalues of the action of
$\iota ^*$
-invariant parts of this fiber, we examine the eigenvalues of the action of
![]() $\iota ^*$
on the tangent space of
$\iota ^*$
on the tangent space of
![]() $\ker j_C$
.
$\ker j_C$
.
We have a short exact sequence on tangent spaces
The tangent space
![]() $T_0A$
is
$T_0A$
is
![]() $H^1(A,\mathcal O_A)$
, and it is
$H^1(A,\mathcal O_A)$
, and it is
![]() $2$
-dimensional with
$2$
-dimensional with
![]() $\iota ^*$
acting as multiplication by
$\iota ^*$
acting as multiplication by
![]() $-1$
. The tangent space
$-1$
. The tangent space
![]() $T_0\operatorname {\mathrm {Pic}}^0_C$
is
$T_0\operatorname {\mathrm {Pic}}^0_C$
is
![]() $H^1(C,\mathcal O_C) \cong H^0(C,\omega _C)^*$
, which is
$H^1(C,\mathcal O_C) \cong H^0(C,\omega _C)^*$
, which is
![]() $4$
-dimensional. On the other hand, tensoring the short exact sequence
$4$
-dimensional. On the other hand, tensoring the short exact sequence
with
![]() $L\cong \mathcal O_A(C)$
gives
$L\cong \mathcal O_A(C)$
gives
By adjunction,
![]() $\mathcal O_C(C)\cong \omega _C$
, so we have the following long exact sequence:
$\mathcal O_C(C)\cong \omega _C$
, so we have the following long exact sequence:
The map
![]() $H^0(A,\mathcal O_A)\to H^0(A,L)$
sends the generator of the
$H^0(A,\mathcal O_A)\to H^0(A,L)$
sends the generator of the
![]() $1$
-dimensional space
$1$
-dimensional space
![]() $H^0(A,\mathcal O_A)$
to
$H^0(A,\mathcal O_A)$
to
![]() $[C]$
. Putting all of this together, the eigenvalues and dimensions of eigenspaces of
$[C]$
. Putting all of this together, the eigenvalues and dimensions of eigenspaces of
![]() $\iota ^*$
acting on the tangent space of
$\iota ^*$
acting on the tangent space of
![]() $\ker j_C$
are equal to those of
$\ker j_C$
are equal to those of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $H^0(A,L)/[C]$
.
$H^0(A,L)/[C]$
.
Suppose
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
. Then, by Proposition 6.5, the eigenvalues of
$C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
. Then, by Proposition 6.5, the eigenvalues of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $H^0(A,L)/[C]$
are both the same: if
$H^0(A,L)/[C]$
are both the same: if
![]() $q_L$
is even, they are both
$q_L$
is even, they are both
![]() $+1$
, and if
$+1$
, and if
![]() $q_L$
is odd, they are both
$q_L$
is odd, they are both
![]() $-1$
. In each case, these eigenvalues are different from the eigenvalue of the action of
$-1$
. In each case, these eigenvalues are different from the eigenvalue of the action of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $[C]$
. If, instead,
$[C]$
. If, instead,
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
, then for
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
, then for
![]() $q_L$
even or odd, the eigenvalues of
$q_L$
even or odd, the eigenvalues of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $H^0(A,L)/[C]$
are
$H^0(A,L)/[C]$
are
![]() $+1$
and
$+1$
and
![]() $-1$
.
$-1$
.
The tangent space of the fiber of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
over
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}\sqcup {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
is isomorphic to the eigenspace of
$C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}\sqcup {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
is isomorphic to the eigenspace of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $T_0\ker j_C$
with the same eigenvalue as the action of
$T_0\ker j_C$
with the same eigenvalue as the action of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $[C]$
. Thus,
$[C]$
. Thus,
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
has
$\operatorname {\mathrm {Fix}}(\iota ^*)$
has
![]() $0$
-dimensional fibers over
$0$
-dimensional fibers over
![]() ${\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
and generically
${\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
and generically
![]() $1$
-dimensional fibers over
$1$
-dimensional fibers over
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}} \cong {\mathbb P}^1$
. For any
${\mathbb P} V_{\operatorname {\mathrm {ell}}} \cong {\mathbb P}^1$
. For any
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
that is smooth, the fiber of
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
that is smooth, the fiber of
![]() $j_C$
over
$j_C$
over
![]() $0_A$
is
$0_A$
is
![]() $2$
-dimensional and so must be an abelian surface. Since
$2$
-dimensional and so must be an abelian surface. Since
![]() $\iota ^*$
acts with two different eigenvalues on the tangent space of
$\iota ^*$
acts with two different eigenvalues on the tangent space of
![]() $\ker j_C$
, it must be, up to isogeny, the product of two elliptic curves.
$\ker j_C$
, it must be, up to isogeny, the product of two elliptic curves.
Generically, curves
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
are smooth, and as mentioned above,
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
are smooth, and as mentioned above,
![]() $C/\iota $
is an elliptic curve. Since the quotient map
$C/\iota $
is an elliptic curve. Since the quotient map
![]() $C\to C/\iota $
is a ramified cyclic double cover mapping between smooth varieties, pullback induces an inclusion
$C\to C/\iota $
is a ramified cyclic double cover mapping between smooth varieties, pullback induces an inclusion
![]() $\operatorname {\mathrm {Pic}}^0(C/\iota )\hookrightarrow \operatorname {\mathrm {Pic}}^0(C)$
. We may represent any point in the image as
$\operatorname {\mathrm {Pic}}^0(C/\iota )\hookrightarrow \operatorname {\mathrm {Pic}}^0(C)$
. We may represent any point in the image as
![]() $\mathcal O(x+\iota (x))$
for some
$\mathcal O(x+\iota (x))$
for some
![]() $x\in C$
. Such line bundles are in
$x\in C$
. Such line bundles are in
![]() $\ker j_C$
. Similarly, there is an inclusion of
$\ker j_C$
. Similarly, there is an inclusion of
![]() $\smash {\operatorname {\mathrm {Pic}}^d_{C/\iota }}$
into
$\smash {\operatorname {\mathrm {Pic}}^d_{C/\iota }}$
into
![]() $(\varphi _C^{-1}(M))^{\iota ^*}$
, and by the tangent space calculation, we see that generically these elliptic curves
$(\varphi _C^{-1}(M))^{\iota ^*}$
, and by the tangent space calculation, we see that generically these elliptic curves
![]() $\operatorname {\mathrm {Pic}}^d_{C/\iota }\cong C/\iota $
are the
$\operatorname {\mathrm {Pic}}^d_{C/\iota }\cong C/\iota $
are the
![]() $1$
-dimensional part of the fiber of f over C.
$1$
-dimensional part of the fiber of f over C.
In the case of
![]() $K_A(0,l,-1)$
, we are able to give the following refinement by a different argument.
$K_A(0,l,-1)$
, we are able to give the following refinement by a different argument.
Proposition 6.7. The fixed locus of
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $K_A(0,l,-1)$
consists of the Kummer K3 surface
$K_A(0,l,-1)$
consists of the Kummer K3 surface
![]() $K_1(A)\cong K_1(\hat {A})$
and 36 isolated points.
$K_1(A)\cong K_1(\hat {A})$
and 36 isolated points.
Proof. Hassett and Tschinkel [Reference Honigs21] and Tarí [Reference Tarí54] showed that the fixed locus of a symplectic involution on
![]() $K_2(A)$
consists of the Kummer K3 surface
$K_2(A)$
consists of the Kummer K3 surface
![]() $K_1(A)$
and 36 additional isolated points.
$K_1(A)$
and 36 additional isolated points.
As discussed in Example 5.4(b), a series of derived equivalences compatible with
![]() $\iota ^*$
gives an isomorphism
$\iota ^*$
gives an isomorphism
![]() $K_A(0,l,-1)\cong K_{\hat {A}}(1,0,-3)$
. Hence, the K3 surface in the fixed locus of
$K_A(0,l,-1)\cong K_{\hat {A}}(1,0,-3)$
. Hence, the K3 surface in the fixed locus of
![]() $\iota ^*$
acting on
$\iota ^*$
acting on
![]() $K_A(0,l,-1)$
is isomorphic to
$K_A(0,l,-1)$
is isomorphic to
![]() $K_1(\hat {A})$
, which is isomorphic over
$K_1(\hat {A})$
, which is isomorphic over
![]() ${\mathbb C}$
to
${\mathbb C}$
to
![]() $K_1(A)$
[Reference Hudson and Barth24, Reference Stellari53].
$K_1(A)$
[Reference Hudson and Barth24, Reference Stellari53].
7 A
 $(1,3)$
-polarized example: Singular fibers of an elliptic K3
$(1,3)$
-polarized example: Singular fibers of an elliptic K3
The proof of Proposition 6.6 shows that the fibration
![]() $K_A(0,l,s) \to |L|$
restricts to a fibration
$K_A(0,l,s) \to |L|$
restricts to a fibration
![]() $\operatorname {\mathrm {Fix}}(\iota ^*) \to {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
, and when
$\operatorname {\mathrm {Fix}}(\iota ^*) \to {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
, and when
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
is smooth, the fiber of
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
is smooth, the fiber of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
over C is isomorphic to
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over C is isomorphic to
![]() $\operatorname {\mathrm {Pic}}^d_{C/\iota }$
. It remains to examine the fibers in
$\operatorname {\mathrm {Pic}}^d_{C/\iota }$
. It remains to examine the fibers in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
over curves in
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over curves in
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
that are singular. We show below that the singular fibers are the same as the singular fibers of a natural elliptic fibration of the Kummer K3 of A, which we now describe.
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
that are singular. We show below that the singular fibers are the same as the singular fibers of a natural elliptic fibration of the Kummer K3 of A, which we now describe.
In [Reference O’Grady48], Naruki analyzes an elliptic fibration of Kummer K3 surfaces that are constructed from
![]() $(1,3)$
-polarized abelian surfaces. He uses the linear system
$(1,3)$
-polarized abelian surfaces. He uses the linear system
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
of Proposition 6.5 to induce a linear system we will call W on
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
of Proposition 6.5 to induce a linear system we will call W on
![]() $K_1(A)$
, which yields an elliptic fibration
$K_1(A)$
, which yields an elliptic fibration
![]() $K_1(A) \to {\mathbb P}^1$
whose fibers are generically
$K_1(A) \to {\mathbb P}^1$
whose fibers are generically
![]() $C/\iota $
for
$C/\iota $
for
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. Since
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. Since
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
must have arithmetic genus
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
must have arithmetic genus
![]() $4$
and pass through at least
$4$
and pass through at least
![]() $6$
points in
$6$
points in
![]() $A[2]$
, Riemann–Hurwitz shows that if
$A[2]$
, Riemann–Hurwitz shows that if
![]() $C/\iota $
is a smooth elliptic curve, then C must be smooth as well and pass through exactly
$C/\iota $
is a smooth elliptic curve, then C must be smooth as well and pass through exactly
![]() $6$
points in
$6$
points in
![]() $A[2]$
.
$A[2]$
.
Proposition 7.1 (Naruki [Reference O’Grady48, §4])
Under a genericity assumption on A [Reference O’Grady48, p. 224, (GA)], the linear system W has:
-
(i) Four singular fibers of type
 $I_1$
.
$I_1$
. -
(ii) Ten singular fibers of type
 $I_2$
. There is one fiber of this type for each point of
$I_2$
. There is one fiber of this type for each point of
 $A[2]$
that is not in the base locus of
$A[2]$
that is not in the base locus of
 ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. The line in
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. The line in
 $K_1(A)$
that is the blow up of this point is contained in the fiber.
$K_1(A)$
that is the blow up of this point is contained in the fiber.
We show that the same is true for
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
:
$\operatorname {\mathrm {Fix}}(\iota ^*)$
:
Theorem 7.2. Let A be an abelian surface satisfying the hypotheses at the beginning of the section such that the singular fibers of W consist of four fibers of type
![]() $I_1$
and ten fibers of type
$I_1$
and ten fibers of type
![]() $I_2$
, as in Proposition 7.1. Then, for any s,
$I_2$
, as in Proposition 7.1. Then, for any s,
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
contains an elliptically fibered K3 whose singular fibers are of the same type.
$\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
contains an elliptically fibered K3 whose singular fibers are of the same type.
Proof. We split the proof into two parts. In Proposition 7.3 below, we show that there are 4 fibers of type
![]() $I_1$
. In Proposition 7.4, we show that there are 10 fibers of type
$I_1$
. In Proposition 7.4, we show that there are 10 fibers of type
![]() $I_2$
.
$I_2$
.
For topological reasons, this must be all of the one-dimensional locus of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
. Indeed, the
$\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
. Indeed, the
![]() $4$
singular fibers of type
$4$
singular fibers of type
![]() $I_1$
and
$I_1$
and
![]() $10$
singular fibers of type
$10$
singular fibers of type
![]() $I_2$
account for the fact that the topological Euler number of a K3 surface is
$I_2$
account for the fact that the topological Euler number of a K3 surface is
![]() $24$
[Reference Huybrechts and Lehn27, Rmk. 11.1.12].
$24$
[Reference Huybrechts and Lehn27, Rmk. 11.1.12].
Proposition 7.3. Let
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be a curve inducing a genus
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be a curve inducing a genus
![]() $1$
singular curve
$1$
singular curve
![]() $C/\iota $
of type
$C/\iota $
of type
![]() $I_1$
in W. Then,
$I_1$
in W. Then,
![]() $\smash {\overline {\mathrm {Pic}}{}^0_{C/\iota }\cong \overline {\mathrm {Pic}}{}^d_{C/\iota }}$
is a singular curve of type
$\smash {\overline {\mathrm {Pic}}{}^0_{C/\iota }\cong \overline {\mathrm {Pic}}{}^d_{C/\iota }}$
is a singular curve of type
![]() $I_1$
and includes into
$I_1$
and includes into
![]() $(\ker j_C)^{\iota ^*}$
.
$(\ker j_C)^{\iota ^*}$
.
Proof. By assumption, the curve
![]() $C/\iota $
is of type
$C/\iota $
is of type
![]() $I_1$
and hence has arithmetic genus
$I_1$
and hence has arithmetic genus
![]() $1$
with one nodal singularity. Applying the Riemann–Hurwitz formula for singular curves [Reference Green, Kim, Laza and Robles18, (1.2)] to the double cover
$1$
with one nodal singularity. Applying the Riemann–Hurwitz formula for singular curves [Reference Green, Kim, Laza and Robles18, (1.2)] to the double cover
![]() $C\to C/\iota $
, we see the arithmetic genus
$C\to C/\iota $
, we see the arithmetic genus
![]() $4$
curve C has geometric genus
$4$
curve C has geometric genus
![]() $2$
with
$2$
with
![]() $6$
ramification points, so it must have two singular points that are exchanged by
$6$
ramification points, so it must have two singular points that are exchanged by
![]() $\iota $
. We call these points x and
$\iota $
. We call these points x and
![]() $\iota x$
and then write
$\iota x$
and then write
![]() $[x,\iota x]$
for the singular point of
$[x,\iota x]$
for the singular point of
![]() $C/\iota $
.
$C/\iota $
.
Consider the induced map on the normalizations of these curves:
![]() $C^{\nu }\to (C/\iota )^{\nu }$
. Since this is a ramified double cover of curves, the pullback map
$C^{\nu }\to (C/\iota )^{\nu }$
. Since this is a ramified double cover of curves, the pullback map
![]() $\operatorname {\mathrm {Pic}}^0((C/\iota )^{\nu })\to \operatorname {\mathrm {Pic}}^0(C^{\nu })$
is an inclusion. We have the following map between short exact sequences of groups:
$\operatorname {\mathrm {Pic}}^0((C/\iota )^{\nu })\to \operatorname {\mathrm {Pic}}^0(C^{\nu })$
is an inclusion. We have the following map between short exact sequences of groups:

The elements of
![]() ${\mathbb C}^*$
correspond to all possible choices for identifying the two fibers over a given node. The vertical maps are pullbacks along quotient maps, and
${\mathbb C}^*$
correspond to all possible choices for identifying the two fibers over a given node. The vertical maps are pullbacks along quotient maps, and
![]() ${\mathbb C}^*\to {\mathbb C}^*\oplus {\mathbb C}^*$
is the diagonal map, which corresponds to a choice of gluing a line bundle at the node on
${\mathbb C}^*\to {\mathbb C}^*\oplus {\mathbb C}^*$
is the diagonal map, which corresponds to a choice of gluing a line bundle at the node on
![]() $C/\iota $
getting mapped to the same choice of gluing at each of the nodes on C. By the five lemma, the map
$C/\iota $
getting mapped to the same choice of gluing at each of the nodes on C. By the five lemma, the map
![]() $\operatorname {\mathrm {Pic}}^0(C/\iota )\to \operatorname {\mathrm {Pic}}^0(C)$
is an injection.
$\operatorname {\mathrm {Pic}}^0(C/\iota )\to \operatorname {\mathrm {Pic}}^0(C)$
is an injection.
The Abel map (see Section 6.2) shows the points in
![]() $\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }}$
correspond to points on the curve
$\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }}$
correspond to points on the curve
![]() $C/\iota $
, and all its elements are line bundles except for the sheaf corresponding to the singular point of
$C/\iota $
, and all its elements are line bundles except for the sheaf corresponding to the singular point of
![]() $C/\iota $
.
$C/\iota $
.
The pullback map
![]() $\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }\to \overline {\mathrm {Pic}}{}^{-2}_{C}}$
sends
$\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }\to \overline {\mathrm {Pic}}{}^{-2}_{C}}$
sends
![]() $\mathcal L([x,\iota x])$
to
$\mathcal L([x,\iota x])$
to
![]() $\mathcal L([x]+[\iota x])$
, which is also not a line bundle and maps to
$\mathcal L([x]+[\iota x])$
, which is also not a line bundle and maps to
![]() $0$
under
$0$
under
![]() $\varphi _C$
. Thus, this pullback map is an injection. The sheaf
$\varphi _C$
. Thus, this pullback map is an injection. The sheaf
![]() $\mathcal L([x,\iota x])$
is fixed by
$\mathcal L([x,\iota x])$
is fixed by
![]() $\iota ^*$
. We may choose an isomorphism
$\iota ^*$
. We may choose an isomorphism
![]() $\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }\cong \overline {\mathrm {Pic}}{}^0_{C/\iota }}$
compatible with
$\smash {\overline {\mathrm {Pic}}{}^{-1}_{C/\iota }\cong \overline {\mathrm {Pic}}{}^0_{C/\iota }}$
compatible with
![]() $\iota ^*$
to see that
$\iota ^*$
to see that
![]() $\smash {\overline {\mathrm {Pic}}{}^0_{C/\iota }}$
includes into
$\smash {\overline {\mathrm {Pic}}{}^0_{C/\iota }}$
includes into
![]() $(\ker {j_C})^{\iota ^*}$
.
$(\ker {j_C})^{\iota ^*}$
.
By Proposition 6.1,
![]() $\overline {\mathrm {Pic}}{}^0_{C/\iota }$
is a singular curve of type
$\overline {\mathrm {Pic}}{}^0_{C/\iota }$
is a singular curve of type
![]() $I_1$
.
$I_1$
.
Proposition 7.4. Let
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be a curve inducing a genus
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be a curve inducing a genus
![]() $1$
singular curve X of type
$1$
singular curve X of type
![]() $I_2$
in W. Then,
$I_2$
in W. Then,
![]() $(\ker {j_C})^{\iota ^*}$
contains a curve of type
$(\ker {j_C})^{\iota ^*}$
contains a curve of type
![]() $I_2$
.
$I_2$
.
Proof. By the discussion in [Reference O’Grady48], the curve X in the linear system W that corresponds to C is the intersection of a line and a conic. The line in X is the blowup of a point
![]() $q\in A[2]$
that is one of the
$q\in A[2]$
that is one of the
![]() $10$
such not in the base locus of
$10$
such not in the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. The curve C thus has a node at q. The normalization
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
. The curve C thus has a node at q. The normalization
![]() $f \colon C^{\nu } \to C$
inherits an action of
$f \colon C^{\nu } \to C$
inherits an action of
![]() $\iota $
, and the quotient
$\iota $
, and the quotient
![]() $C^{\nu }/\iota $
is the conic contained in X. Thus,
$C^{\nu }/\iota $
is the conic contained in X. Thus,
![]() $C^{\nu }$
is hyperelliptic and as a double cover of
$C^{\nu }$
is hyperelliptic and as a double cover of
![]() $C^{\nu }/\iota $
, it is ramified at
$C^{\nu }/\iota $
, it is ramified at
![]() $8$
points, consisting of the six points
$8$
points, consisting of the six points
![]() $p_1,\ldots ,p_6$
in the base locus of
$p_1,\ldots ,p_6$
in the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
and the two points above q (named
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
and the two points above q (named
![]() $q_1,q_2$
). By Riemann–Hurwitz,
$q_1,q_2$
). By Riemann–Hurwitz,
![]() $C^{\nu }$
has genus
$C^{\nu }$
has genus
![]() $3$
. Thus, C has arithmetic genus
$3$
. Thus, C has arithmetic genus
![]() $4$
and geometric genus
$4$
and geometric genus
![]() $3$
, so the node at p is its unique singularity.
$3$
, so the node at p is its unique singularity.
Via Altman and Kleiman’s presentation schemes [Reference Barth and Nieto3], we have the following description of
![]() $\overline {\mathrm {Pic}}{}^0_C$
(cf. [Reference Kass32, §3.3]). Pullback by the normalization map
$\overline {\mathrm {Pic}}{}^0_C$
(cf. [Reference Kass32, §3.3]). Pullback by the normalization map
![]() $f:C^{\nu }\to C$
gives the short exact sequence on Picard groups
$f:C^{\nu }\to C$
gives the short exact sequence on Picard groups
where, again, the elements of
![]() ${\mathbb C}^*$
correspond to all possible choices for identifying the two fibers over q. The presentation scheme of f gives a
${\mathbb C}^*$
correspond to all possible choices for identifying the two fibers over q. The presentation scheme of f gives a
![]() ${\mathbb P}^1$
-bundle
${\mathbb P}^1$
-bundle
![]() $\pi \colon P\to \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, where the fiber over a point
$\pi \colon P\to \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, where the fiber over a point
![]() $I'\in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
is given by presentations of
$I'\in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
is given by presentations of
![]() $I'$
; that is, short exact sequences of sheaves on C of the following form:
$I'$
; that is, short exact sequences of sheaves on C of the following form:
It follows that
![]() $I\in \overline {\mathrm {Pic}}{}^0_C$
, so there is a natural morphism
$I\in \overline {\mathrm {Pic}}{}^0_C$
, so there is a natural morphism
![]() $\kappa \colon P \to \overline {\mathrm {Pic}}{}^0_C$
, which is an isomorphism when restricted to the preimage of
$\kappa \colon P \to \overline {\mathrm {Pic}}{}^0_C$
, which is an isomorphism when restricted to the preimage of
![]() $\operatorname {\mathrm {Pic}}^0_C\subset \overline {\mathrm {Pic}}{}^0_C$
. For each
$\operatorname {\mathrm {Pic}}^0_C\subset \overline {\mathrm {Pic}}{}^0_C$
. For each
![]() $I' \in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, there is a
$I' \in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, there is a
![]() ${\mathbb C}^* \subset {\mathbb P}^1=\pi ^{-1}(I')$
, exactly the
${\mathbb C}^* \subset {\mathbb P}^1=\pi ^{-1}(I')$
, exactly the
![]() ${\mathbb C}^*$
of (7.1), which gets mapped injectively under
${\mathbb C}^*$
of (7.1), which gets mapped injectively under
![]() $\kappa $
into
$\kappa $
into
![]() $\operatorname {\mathrm {Pic}}^0_C$
.
$\operatorname {\mathrm {Pic}}^0_C$
.
Furthermore, there is a closed embedding
![]() $\varepsilon '\colon \operatorname {\mathrm {Pic}}^0_{C^{\nu }} \times \{q_1,q_2\} \hookrightarrow P$
, which sends a pair
$\varepsilon '\colon \operatorname {\mathrm {Pic}}^0_{C^{\nu }} \times \{q_1,q_2\} \hookrightarrow P$
, which sends a pair
![]() $(I',q_i)$
to the presentation
$(I',q_i)$
to the presentation
This gives the description of the rest of the
![]() ${\mathbb P}^1$
-fiber of
${\mathbb P}^1$
-fiber of
![]() $\pi $
over a point
$\pi $
over a point
![]() $I' \in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
: these are the two points compactifying the
$I' \in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
: these are the two points compactifying the
![]() ${\mathbb C}^*$
described above. Thus, to complete the description of
${\mathbb C}^*$
described above. Thus, to complete the description of
![]() $\overline {\mathrm {Pic}}{}^0_C$
, it remains to describe
$\overline {\mathrm {Pic}}{}^0_C$
, it remains to describe
![]() $\kappa $
restricted to
$\kappa $
restricted to
![]() $\varepsilon '(\operatorname {\mathrm {Pic}}^0_{C^{\nu }} \times \{q_1,q_2\})$
.
$\varepsilon '(\operatorname {\mathrm {Pic}}^0_{C^{\nu }} \times \{q_1,q_2\})$
.
Here,
![]() $\kappa $
is
$\kappa $
is
![]() $2$
-to-
$2$
-to-
![]() $1$
, but does not just trivially glue the two copies of
$1$
, but does not just trivially glue the two copies of
![]() $\operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
together. Rather, they are glued with a twist:
$\operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
together. Rather, they are glued with a twist:
Since
![]() $C^{\nu }$
is hyperelliptic,
$C^{\nu }$
is hyperelliptic,
![]() $2q_1 \sim _{\text {lin}} 2q_2$
and
$2q_1 \sim _{\text {lin}} 2q_2$
and
![]() $\mathcal O(q_1-q_2)$
is
$\mathcal O(q_1-q_2)$
is
![]() $2$
-torsion in
$2$
-torsion in
![]() $\operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, which further implies that
$\operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
, which further implies that
With this observation in hand, we now describe the one-dimensional component of the locus of
![]() $\overline {\mathrm {Pic}}{}^0_C$
that is in
$\overline {\mathrm {Pic}}{}^0_C$
that is in
![]() $(\ker j_C)^{\iota ^*}$
. While we are working in
$(\ker j_C)^{\iota ^*}$
. While we are working in
![]() $\overline {\mathrm {Pic}}{}^0_C$
, we will instead consider the fiber over
$\overline {\mathrm {Pic}}{}^0_C$
, we will instead consider the fiber over
![]() $0_A$
of
$0_A$
of
![]() $\varphi _C$
. By abuse of notation, we will also call this
$\varphi _C$
. By abuse of notation, we will also call this
![]() $\ker \varphi _C$
.
$\ker \varphi _C$
.
Claim 7.5. The locus of
![]() $\overline {\mathrm {Pic}}{}^0_C$
that is both fixed by
$\overline {\mathrm {Pic}}{}^0_C$
that is both fixed by
![]() $\iota ^*$
and is in
$\iota ^*$
and is in
![]() $\ker \varphi _C$
contains
$\ker \varphi _C$
contains
which is two copies of
![]() ${\mathbb P}^1$
intersecting at two points (i.e., a singular curve of type
${\mathbb P}^1$
intersecting at two points (i.e., a singular curve of type
![]() $I_2$
).
$I_2$
).
Proof. First, we observe that if
![]() $I'\in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
is fixed by
$I'\in \operatorname {\mathrm {Pic}}^0_{C^{\nu }}$
is fixed by
![]() $\iota ^*$
, and
$\iota ^*$
, and
is a presentation of
![]() $I'$
, then I is also fixed by
$I'$
, then I is also fixed by
![]() $\iota ^*$
. Indeed, by push-pull, we know that
$\iota ^*$
. Indeed, by push-pull, we know that
![]() $f_*\iota ^*I'\cong \iota ^*f_*I'$
. We have the short exact sequence
$f_*\iota ^*I'\cong \iota ^*f_*I'$
. We have the short exact sequence
so if
![]() $I'$
is fixed by
$I'$
is fixed by
![]() $\iota ^*$
, then
$\iota ^*$
, then
![]() $I\cong \iota ^*I$
. Thus, if
$I\cong \iota ^*I$
. Thus, if
![]() $I'$
is fixed, then the whole
$I'$
is fixed, then the whole
![]() ${\mathbb P}^1$
-fiber in P is pointwise fixed as well. Note also that, given a short exact sequence
${\mathbb P}^1$
-fiber in P is pointwise fixed as well. Note also that, given a short exact sequence
![]() $0\to I\to f_*I'\to k(q)\to 0$
, if
$0\to I\to f_*I'\to k(q)\to 0$
, if
![]() $I\in \ker \varphi _C$
, then by the discussion in the proof of Lemma 6.2 about the behavior of
$I\in \ker \varphi _C$
, then by the discussion in the proof of Lemma 6.2 about the behavior of
![]() $\varphi _C$
in short exact sequences, so are all the other possible I giving presentations of
$\varphi _C$
in short exact sequences, so are all the other possible I giving presentations of
![]() $I'$
.
$I'$
.
Since there is a short exact sequence
and
![]() $\mathcal O_C\in \ker \varphi _C$
, we know any other kernels of presentations of
$\mathcal O_C\in \ker \varphi _C$
, we know any other kernels of presentations of
![]() $f_*\mathcal O_{C^{\nu }}$
will as well. We also have that
$f_*\mathcal O_{C^{\nu }}$
will as well. We also have that
![]() $\mathcal O_{C^{\nu }}$
is fixed by
$\mathcal O_{C^{\nu }}$
is fixed by
![]() $\iota ^*$
, so it follows that
$\iota ^*$
, so it follows that
![]() $\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
is both fixed by
$\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
is both fixed by
![]() $\iota ^*$
and in
$\iota ^*$
and in
![]() $\ker \varphi _C$
.
$\ker \varphi _C$
.
The same holds for
![]() $\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}(q_1-q_2))$
: since
$\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}(q_1-q_2))$
: since
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are fixed by
$q_2$
are fixed by
![]() $\iota $
,
$\iota $
,
![]() $\mathcal O_{C^{\nu }}(q_1-q_2)$
is fixed by
$\mathcal O_{C^{\nu }}(q_1-q_2)$
is fixed by
![]() $\iota ^*$
, and we will show that any presentation is sent to
$\iota ^*$
, and we will show that any presentation is sent to
![]() $0$
by
$0$
by
![]() $\varphi _C$
. For a presentation
$\varphi _C$
. For a presentation
applying the inclusion
![]() $h_C:C\hookrightarrow A$
and
$h_C:C\hookrightarrow A$
and
![]() $\Phi _P$
, we have
$\Phi _P$
, we have
There is also a presentation
which gives
and hence,
On the other hand, there is a presentation
so
![]() $f_*\mathcal O_{C^{\nu }}(-q_1)\in \kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
, which we showed above is in
$f_*\mathcal O_{C^{\nu }}(-q_1)\in \kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
, which we showed above is in
![]() $\ker \varphi _C$
. Thus, the same is true for I.
$\ker \varphi _C$
. Thus, the same is true for I.
It remains to show that these two
![]() ${\mathbb P}^1$
’s in
${\mathbb P}^1$
’s in
![]() $\overline {\mathrm {Pic}}{}^0_C$
are glued together at two points. But this follows from the description of
$\overline {\mathrm {Pic}}{}^0_C$
are glued together at two points. But this follows from the description of
![]() $\overline {\mathrm {Pic}}{}^0_C$
, since
$\overline {\mathrm {Pic}}{}^0_C$
, since
and
While above we work in degree
![]() $0$
, we can twist by a degree d line bundle on C to get the description in
$0$
, we can twist by a degree d line bundle on C to get the description in
![]() $\overline {\mathrm {Pic}}{}^d_C$
. This completes the proof of Proposition 7.4.
$\overline {\mathrm {Pic}}{}^d_C$
. This completes the proof of Proposition 7.4.
Remark 7.6. It is interesting to consider
![]() $(\ker j_C)^{\iota ^*}$
in Propostion 7.4 from the point of view of the Abel map. We consider the case where
$(\ker j_C)^{\iota ^*}$
in Propostion 7.4 from the point of view of the Abel map. We consider the case where
![]() $d=-4$
. The fixed locus
$d=-4$
. The fixed locus
![]() $(\ker j_C)^{\iota ^*}\subseteq \overline {\mathrm {Pic}}{}_C^{-4}$
contains all divisors of the form
$(\ker j_C)^{\iota ^*}\subseteq \overline {\mathrm {Pic}}{}_C^{-4}$
contains all divisors of the form
![]() $-(x+\iota x+ y+\iota y)$
for
$-(x+\iota x+ y+\iota y)$
for
![]() $x,y\in C$
, but the information from the Abel map alone does not make clear which of these divisors get identified under linear equivalence in
$x,y\in C$
, but the information from the Abel map alone does not make clear which of these divisors get identified under linear equivalence in
![]() $\overline {\mathrm {Pic}}{}_C^{-4}$
. We will show that these divisors are all contained in the curve from Proposition 7.4. We may choose an isomorphism
$\overline {\mathrm {Pic}}{}_C^{-4}$
. We will show that these divisors are all contained in the curve from Proposition 7.4. We may choose an isomorphism
![]() $\overline {\mathrm {Pic}}{}^0_C\cong \overline {\mathrm {Pic}}{}^{-4}_C$
by subtracting four copies of a
$\overline {\mathrm {Pic}}{}^0_C\cong \overline {\mathrm {Pic}}{}^{-4}_C$
by subtracting four copies of a
![]() $2$
-torsion point
$2$
-torsion point
![]() $p\in C$
not at the node. Let
$p\in C$
not at the node. Let
![]() $p'\in C^{\nu }$
be preimage of p under the normalization map. Since
$p'\in C^{\nu }$
be preimage of p under the normalization map. Since
![]() $C^{\nu }$
is hyperelliptic,
$C^{\nu }$
is hyperelliptic,
![]() $\mathcal O_{C^{\nu }}(-4p')\cong \mathcal O_{C^{\nu }}(-x'-\iota x'-y'-\iota y')$
, where
$\mathcal O_{C^{\nu }}(-4p')\cong \mathcal O_{C^{\nu }}(-x'-\iota x'-y'-\iota y')$
, where
![]() $x'$
and
$x'$
and
![]() $y'$
are the preimages of x and y in
$y'$
are the preimages of x and y in
![]() $C^{\nu }$
. There is a presentation
$C^{\nu }$
. There is a presentation
so these divisors all lie in the
![]() ${\mathbb P}^1$
corresponding to the twist of
${\mathbb P}^1$
corresponding to the twist of
![]() $\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
.
$\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}))$
.
The divisors
![]() $-(x+\iota x+ y+\iota y)$
correspond to a two-dimensional family in
$-(x+\iota x+ y+\iota y)$
correspond to a two-dimensional family in
![]() $\operatorname {\mathrm {Hilb}}^4_C$
, but their image in
$\operatorname {\mathrm {Hilb}}^4_C$
, but their image in
![]() $\overline {\mathrm {Pic}}{}^{-4}_C$
is at most
$\overline {\mathrm {Pic}}{}^{-4}_C$
is at most
![]() $1$
-dimensional, so they must lie in the exceptional locus of the Abel map. Since C is not hyperelliptic, the canonical morphism gives a closed immersion into
$1$
-dimensional, so they must lie in the exceptional locus of the Abel map. Since C is not hyperelliptic, the canonical morphism gives a closed immersion into
![]() ${\mathbb P}^3$
and divisors in the exceptional locus are those that lie on a hyperplane in
${\mathbb P}^3$
and divisors in the exceptional locus are those that lie on a hyperplane in
![]() ${\mathbb P}^3$
; we see there must be an interaction of these planes with the action of
${\mathbb P}^3$
; we see there must be an interaction of these planes with the action of
![]() $\iota $
, but the particulars of it are not immediately clear.
$\iota $
, but the particulars of it are not immediately clear.
It would also be nice to have a description of the elements in
![]() $\overline {\mathrm {Pic}}{}^{-4}_C$
contained in the other copy of
$\overline {\mathrm {Pic}}{}^{-4}_C$
contained in the other copy of
![]() ${\mathbb P}^1$
in
${\mathbb P}^1$
in
![]() $(\ker j_C)^{\iota ^*}$
. Since the canonical bundle
$(\ker j_C)^{\iota ^*}$
. Since the canonical bundle
![]() $\omega _C$
is fixed by
$\omega _C$
is fixed by
![]() $\iota ^*$
and
$\iota ^*$
and
![]() $f^*\omega _C\cong \omega _{C^{\nu }}\otimes \mathcal O_{C^{\nu }}(q_1+q_2)\cong \mathcal O_{C^{\nu }}(4p'+q_1+q_2)$
, line bundles on C which fit into presentations with middle term
$f^*\omega _C\cong \omega _{C^{\nu }}\otimes \mathcal O_{C^{\nu }}(q_1+q_2)\cong \mathcal O_{C^{\nu }}(4p'+q_1+q_2)$
, line bundles on C which fit into presentations with middle term
![]() $f_*\left (f^*\omega _C^{-1}\otimes \mathcal O_{C^{\nu }}(x'+\iota x')\right )$
lie in the
$f_*\left (f^*\omega _C^{-1}\otimes \mathcal O_{C^{\nu }}(x'+\iota x')\right )$
lie in the
![]() ${\mathbb P}^1$
corresponding to the twist of
${\mathbb P}^1$
corresponding to the twist of
![]() $\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}(q_1-q_2))$
. However, the question of exactly which effective divisors give rise to these line bundles is again dependent on the geometry of the canonical embedding.
$\kappa (\pi ^{-1}(\mathcal O_{C^{\nu }}(q_1-q_2))$
. However, the question of exactly which effective divisors give rise to these line bundles is again dependent on the geometry of the canonical embedding.
Remark 7.7. In this section we have shown that the elliptic K3 surface in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
has the same types of singular fibers as those in the fibration of the Kummer K3 surface studied by Naruki [Reference O’Grady48]. By Proposition 6.7 for
$\operatorname {\mathrm {Fix}}(\iota ^*)$
has the same types of singular fibers as those in the fibration of the Kummer K3 surface studied by Naruki [Reference O’Grady48]. By Proposition 6.7 for
![]() $K_A(0,l,-1)$
, the K3 surface in the fixed-point locus is isomorphic to the Kummer K3 surface. However, it is not apparent that, in general, there is any kind of natural map from the K3 surface studied by Naruki to
$K_A(0,l,-1)$
, the K3 surface in the fixed-point locus is isomorphic to the Kummer K3 surface. However, it is not apparent that, in general, there is any kind of natural map from the K3 surface studied by Naruki to
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
, or that these fixed-point loci are Kummer K3 surfaces.
$\operatorname {\mathrm {Fix}}(\iota ^*)$
, or that these fixed-point loci are Kummer K3 surfaces.
8 A
 $(1,3)$
-polarized example: Isolated points
$(1,3)$
-polarized example: Isolated points
Finally, we seek a description of the
![]() $36$
isolated points in
$36$
isolated points in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
. We will use a combination of the Abel map and information about the geometry of
$\operatorname {\mathrm {Fix}}(\iota ^*)$
. We will use a combination of the Abel map and information about the geometry of
![]() $2$
-torsion points in a
$2$
-torsion points in a
![]() $(1,3)$
-polarized abelian surface to finish our description of the fixed loci.
$(1,3)$
-polarized abelian surface to finish our description of the fixed loci.
8.1 Geometry of
 $A[2]$
$A[2]$
The description of the isolated points in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
will require an understanding of line bundles on curves
$\operatorname {\mathrm {Fix}}(\iota ^*)\subset K_A(0,l,s)$
will require an understanding of line bundles on curves
![]() $C \in |L|^{\iota ^*}$
corresponding to divisors which sum to
$C \in |L|^{\iota ^*}$
corresponding to divisors which sum to
![]() $0$
in A.
$0$
in A.
As discussed in [Reference Beckmann4], the line bundle
![]() $L^2$
on our
$L^2$
on our
![]() $(1,3)$
-polarized abelian surface gives an embedding of the desingularized Kummer K3 surface into
$(1,3)$
-polarized abelian surface gives an embedding of the desingularized Kummer K3 surface into
![]() ${\mathbb P}^3$
. They describe an action of the Heisenberg group on
${\mathbb P}^3$
. They describe an action of the Heisenberg group on
![]() ${\mathbb P}^3$
that connects the geometry of the group action of elements
${\mathbb P}^3$
that connects the geometry of the group action of elements
![]() $A[2]$
to the corresponding lines in the Kummer K3 surface.
$A[2]$
to the corresponding lines in the Kummer K3 surface.
We use notation from Hudson’s analysis of
![]() $A[2]$
for principally polarized abelian surfaces [Reference Huybrechts25, Ch. 1,§4], which has the same group structure: We write the group of points of
$A[2]$
for principally polarized abelian surfaces [Reference Huybrechts25, Ch. 1,§4], which has the same group structure: We write the group of points of
![]() $A[2]$
in multiplicative notation in terms of (a not minimal set of) generators
$A[2]$
in multiplicative notation in terms of (a not minimal set of) generators
![]() $1,A,B,C,A',B',C'$
, where
$1,A,B,C,A',B',C'$
, where
![]() $1$
is the identity. The following multiplication tables hold:
$1$
is the identity. The following multiplication tables hold:

Following Naruki [Reference O’Grady48], we see the six points of
![]() $A[2]$
that occur in the base locus of
$A[2]$
that occur in the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
must be a set of six in the group that coincides with those that would lie on a plane in Hudson’s
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
must be a set of six in the group that coincides with those that would lie on a plane in Hudson’s
![]() $(16,6)$
configuration, and so we take the following six points to be in the base locus of
$(16,6)$
configuration, and so we take the following six points to be in the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
:
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
:
Any possible choice of six points will have the same numerical properties described below as they will differ by a translation.
The remaining ten points of
![]() $A[2]$
are then:
$A[2]$
are then:
We will need the following observations in our identification of the isolated fixed points:
Lemma 8.1.
-
(a) The product of any four distinct points in (8.1) cannot be the identity.
-
(b) Given any point in (8.2), there are exactly two ways to then choose three distinct points from those in (8.1) so that the product of the four points is the identity.
-
(c) There are fifteen ways to choose four distinct points from among (8.2) so that their product is the identity.
Proof. The results may be verified directly.
In part (b), for instance, if we choose
![]() $1$
, we have exactly
$1$
, we have exactly
In part (c), the fifteen possibilities are:
 $$ \begin{align*} &(1)(A)(A')(AA') & &(A)(B)(C')(CC') \\ &(1)(B)(B')(BB') & &(A')(B')(C)(CC') \\ &(1)(C)(C')(CC') & &(A)(B')(C)(BB') \\ &(1)(AA')(BB')(CC') & &(A')(B)(C')(BB') \\ &(1)(A)(B)(C) & &(A')(B)(C)(AA') \\ &(1)(A')(B')(C') & &(A)(B')(C')(AA')\\ &(A)(A')(BB')(CC') & &(B)(B')(AA')(CC') \\ & & &(C)(C')(AA')(BB')\\[-39pt] \end{align*} $$
$$ \begin{align*} &(1)(A)(A')(AA') & &(A)(B)(C')(CC') \\ &(1)(B)(B')(BB') & &(A')(B')(C)(CC') \\ &(1)(C)(C')(CC') & &(A)(B')(C)(BB') \\ &(1)(AA')(BB')(CC') & &(A')(B)(C')(BB') \\ &(1)(A)(B)(C) & &(A')(B)(C)(AA') \\ &(1)(A')(B')(C') & &(A)(B')(C')(AA')\\ &(A)(A')(BB')(CC') & &(B)(B')(AA')(CC') \\ & & &(C)(C')(AA')(BB')\\[-39pt] \end{align*} $$
8.2 The fiber of
 $\operatorname {\mathrm {Fix}}(\iota ^*)$
over
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over
 ${\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
${\mathbb P} V_{\operatorname {\mathrm {hyp}}}$
Let
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}\cong {\mathbb P}^0$
. For A a general
$C\in {\mathbb P} V_{\operatorname {\mathrm {hyp}}}\cong {\mathbb P}^0$
. For A a general
![]() $(1,3)$
-polarized abelian surface, C is smooth by [Reference Donovan10, Lem. 3.4], so the kernel of
$(1,3)$
-polarized abelian surface, C is smooth by [Reference Donovan10, Lem. 3.4], so the kernel of
![]() $\varphi _C$
(6.4) is an abelian surface (see Proposition 6.4). The action
$\varphi _C$
(6.4) is an abelian surface (see Proposition 6.4). The action
![]() $\ker \varphi _C$
inherits from
$\ker \varphi _C$
inherits from
![]() $\iota ^*$
on
$\iota ^*$
on
![]() $K(0,l,s)$
is the action of
$K(0,l,s)$
is the action of
![]() $[-1]$
on it as an abelian surface. Thus, there will be exactly
$[-1]$
on it as an abelian surface. Thus, there will be exactly
![]() $16$
isolated fixed points, consisting of the
$16$
isolated fixed points, consisting of the
![]() $2$
-torsion points on
$2$
-torsion points on
![]() $\ker \varphi _C$
.
$\ker \varphi _C$
.
We may also analyze
![]() $(\ker \varphi _C)^{\iota ^*}$
using the Abel map
$(\ker \varphi _C)^{\iota ^*}$
using the Abel map
![]() $\alpha $
from (6.2). Since C is hyperelliptic, the canonical morphism is the degree
$\alpha $
from (6.2). Since C is hyperelliptic, the canonical morphism is the degree
![]() $2$
morphism
$2$
morphism
![]() $\pi \colon C\to {\mathbb P}^1$
. The canonical divisors of C are of the form
$\pi \colon C\to {\mathbb P}^1$
. The canonical divisors of C are of the form
![]() $\pi ^{-1}(t_1)+\pi ^{-1}(t_2)+\pi ^{-1}(t_3)$
for
$\pi ^{-1}(t_1)+\pi ^{-1}(t_2)+\pi ^{-1}(t_3)$
for
![]() $t_1,t_2,t_3\in {\mathbb P}^1$
. The sets of points in
$t_1,t_2,t_3\in {\mathbb P}^1$
. The sets of points in
![]() $\operatorname {\mathrm {Hilb}}^{4}_C$
which sum to
$\operatorname {\mathrm {Hilb}}^{4}_C$
which sum to
![]() $0$
and are fixed by
$0$
and are fixed by
![]() $\iota ^*$
consist of points of the form
$\iota ^*$
consist of points of the form
![]() $\pi ^{-1}(t_1)+\pi ^{-1}(t_2)$
, which are all linearly equivalent, and of four distinct
$\pi ^{-1}(t_1)+\pi ^{-1}(t_2)$
, which are all linearly equivalent, and of four distinct
![]() $2$
-torsion points that sum to
$2$
-torsion points that sum to
![]() $0$
.
$0$
.
From this point of view we find that the sixteen isolated points in
![]() $\operatorname {\mathrm {Pic}}^{-4}_C$
that sum to
$\operatorname {\mathrm {Pic}}^{-4}_C$
that sum to
![]() $0$
and are fixed by
$0$
and are fixed by
![]() $\iota ^*$
are (the negative of) the fifteen points given by Lemma 8.1(c) and the one point that is the image under
$\iota ^*$
are (the negative of) the fifteen points given by Lemma 8.1(c) and the one point that is the image under
![]() $\alpha $
of all points of the form
$\alpha $
of all points of the form
![]() $\pi ^{-1}(t_1)+\pi ^{-1}(t_2)$
.
$\pi ^{-1}(t_1)+\pi ^{-1}(t_2)$
.
This argument may be used to show that the same result holds for
![]() $\operatorname {\mathrm {Pic}}^d_C$
. We can take the isomorphism
$\operatorname {\mathrm {Pic}}^d_C$
. We can take the isomorphism
![]() $\operatorname {\mathrm {Pic}}^{-4}_C\cong \operatorname {\mathrm {Pic}}^d_C$
to be given by adding
$\operatorname {\mathrm {Pic}}^{-4}_C\cong \operatorname {\mathrm {Pic}}^d_C$
to be given by adding
![]() $d+4$
copies of a fixed
$d+4$
copies of a fixed
![]() $2$
-torsion point p, in which case the isomorphism commutes with
$2$
-torsion point p, in which case the isomorphism commutes with
![]() $\iota ^*$
. It is not always possible to choose this isomorphism so that it commutes with taking the kernel of the summation map, but we may instead consider the elements in
$\iota ^*$
. It is not always possible to choose this isomorphism so that it commutes with taking the kernel of the summation map, but we may instead consider the elements in
![]() $\operatorname {\mathrm {Pic}}^d_C$
that sum to
$\operatorname {\mathrm {Pic}}^d_C$
that sum to
![]() $(d+4)\cdot p$
, which amounts to simply performing this calculation in a different fiber of the Albanese map (2.2), which is related to our preferred fiber by an isomorphism.
$(d+4)\cdot p$
, which amounts to simply performing this calculation in a different fiber of the Albanese map (2.2), which is related to our preferred fiber by an isomorphism.
8.3 The fibers of
 $\operatorname {\mathrm {Fix}}(\iota ^*)$
over
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over
 ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
In the last section, we found 16 of the 36 isolated points in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
. To find the rest we examine
$\operatorname {\mathrm {Fix}}(\iota ^*)$
. To find the rest we examine
![]() $(\ker \varphi _C)^{\iota ^*}$
as C varies in
$(\ker \varphi _C)^{\iota ^*}$
as C varies in
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}\cong {\mathbb P}^1$
.
${\mathbb P} V_{\operatorname {\mathrm {ell}}}\cong {\mathbb P}^1$
.
If C is smooth, by our analysis of the tangent space of
![]() $\ker \varphi _C$
in the proof of Proposition 6.6,
$\ker \varphi _C$
in the proof of Proposition 6.6,
![]() $(\ker \varphi _C)^{\iota ^*}$
is isomorphic to the elliptic curve
$(\ker \varphi _C)^{\iota ^*}$
is isomorphic to the elliptic curve
![]() $C/\iota $
, and there are no isolated points.
$C/\iota $
, and there are no isolated points.
Let
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be singular of type
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be singular of type
![]() $I_1$
. Consider the modified Abel map
$I_1$
. Consider the modified Abel map
The curve C passes through exactly six
![]() $2$
-torsion points (8.1) (cf. Proposition 7.3). By Lemma 8.1(a) the only sets of four points on C that sum to
$2$
-torsion points (8.1) (cf. Proposition 7.3). By Lemma 8.1(a) the only sets of four points on C that sum to
![]() $0$
and are fixed by
$0$
and are fixed by
![]() $\iota ^*$
are those of the form
$\iota ^*$
are those of the form
![]() $(x,\iota x,y,\iota y)$
for some
$(x,\iota x,y,\iota y)$
for some
![]() $x,y\in C$
. Points of this form are already contained in the image of the pullback
$x,y\in C$
. Points of this form are already contained in the image of the pullback
![]() $\operatorname {\mathrm {Pic}}_{C/\iota }^0\cong \operatorname {\mathrm {Pic}}_{C/\iota }^{-2}\to \operatorname {\mathrm {Pic}}_{C}^{-4}$
. Thus,
$\operatorname {\mathrm {Pic}}_{C/\iota }^0\cong \operatorname {\mathrm {Pic}}_{C/\iota }^{-2}\to \operatorname {\mathrm {Pic}}_{C}^{-4}$
. Thus,
![]() $(\ker \varphi _C)^{\iota ^*}\cong C/\iota $
, and there are no isolated points.
$(\ker \varphi _C)^{\iota ^*}\cong C/\iota $
, and there are no isolated points.
Now let
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be singular of type
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
be singular of type
![]() $I_2$
. The curve C passes through seven points in
$I_2$
. The curve C passes through seven points in
![]() $A[2]$
: those in the base locus of
$A[2]$
: those in the base locus of
![]() ${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
(see (8.1)) as well as one additional
${\mathbb P} V_{\operatorname {\mathrm {ell}}}$
(see (8.1)) as well as one additional
![]() $2$
-torsion point. The points in
$2$
-torsion point. The points in
![]() $\operatorname {\mathrm {Hilb}}^4_C$
that sum to
$\operatorname {\mathrm {Hilb}}^4_C$
that sum to
![]() $0$
and are fixed by
$0$
and are fixed by
![]() $\iota ^*$
are those of the form
$\iota ^*$
are those of the form
![]() $(x,\iota x,y,\iota y)$
for some
$(x,\iota x,y,\iota y)$
for some
![]() $x,y\in C$
, as well as any tuple of four
$x,y\in C$
, as well as any tuple of four
![]() $2$
-torsion points that sum to
$2$
-torsion points that sum to
![]() $0$
. By Lemma 8.1(a,b), there are exactly two points of the latter form and they are isolated from the points of the former form (cf. Remark 7.6). Thus the fiber of
$0$
. By Lemma 8.1(a,b), there are exactly two points of the latter form and they are isolated from the points of the former form (cf. Remark 7.6). Thus the fiber of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
over C consists precisely of a singular curve of type
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over C consists precisely of a singular curve of type
![]() $I_2$
and two isolated fixed points. There are ten such singular curves, and thus all of the
$I_2$
and two isolated fixed points. There are ten such singular curves, and thus all of the
![]() $36$
isolated points in
$36$
isolated points in
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
are now accounted for.
$\operatorname {\mathrm {Fix}}(\iota ^*)$
are now accounted for.
Remark 8.2. It would be interesting to use the presentation scheme description of
![]() $\overline {\mathrm {Pic}}{}^d_C$
, for
$\overline {\mathrm {Pic}}{}^d_C$
, for
![]() $C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
singular, to identify the two isolated points in the fiber of
$C\in {\mathbb P} V_{\operatorname {\mathrm {ell}}}$
singular, to identify the two isolated points in the fiber of
![]() $\operatorname {\mathrm {Fix}}(\iota ^*)$
over C. For example, what line bundles do they pull back to on
$\operatorname {\mathrm {Fix}}(\iota ^*)$
over C. For example, what line bundles do they pull back to on
![]() $C^{\nu }$
?
$C^{\nu }$
?
Acknowledgements
We heartily thank Nicolas Addington, for pointing us in the direction of this work, and Alexander Polishchuk, for fruitful conversations during the early stages of this project. We also thank Nils Bruin, Maria Fox, Lie Fu, Zhiyuan Li, Eyal Markman, Martin Olsson, John Voight and Chelsea Walton for helpful discussions.
Competing interest
The authors have no competing interests to declare.
Financial support
During the preparation of this article, S.F. was partially supported by NSF DMS-1745670, and K.H. was partially supported by NSERC.