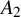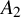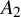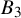1 Introduction
1.1 Deformed rational numbers
The theory of q-deformations of rational numbers has an extremely recent history. Deformed rational numbers were originally introduced in [Reference Morier-Genoud and Ovsienko16] and developed in [Reference Morier-Genoud and Ovsienko15]. The definition considered in these papers is via deformations of continued fraction expansions of rational numbers. The resulting q-rationals enjoy several pleasant properties, and the authors discuss connections to a wide variety of classical topics including the Farey triangulation, cluster algebras and the Jones polynomial.
In this paper, we present an enhancement of the notion of q-deformed rationals, from which the q-rationals of [Reference Morier-Genoud and Ovsienko16] can be easily read off. For any fixed positive q and a rational number
![]() $r/s$
, we describe a pair of real numbers, denoted
$r/s$
, we describe a pair of real numbers, denoted
![]() $[r/s]^{\flat }$
and
$[r/s]^{\flat }$
and
![]() $[r/s]^{\sharp }$
. The number
$[r/s]^{\sharp }$
. The number
![]() $[r/s]^{\sharp }$
is precisely the q-deformation of
$[r/s]^{\sharp }$
is precisely the q-deformation of
![]() $r/s$
considered in [Reference Morier-Genoud and Ovsienko16]. We argue that
$r/s$
considered in [Reference Morier-Genoud and Ovsienko16]. We argue that
![]() $[r/s]^{\flat }$
can also reasonably be thought of as a q-deformation of
$[r/s]^{\flat }$
can also reasonably be thought of as a q-deformation of
![]() $r/s$
.
$r/s$
.
For example, the number
![]() $[1/0]^{\sharp }$
, which is the q-deformation of
$[1/0]^{\sharp }$
, which is the q-deformation of
![]() $\infty $
in [Reference Morier-Genoud and Ovsienko16], is just
$\infty $
in [Reference Morier-Genoud and Ovsienko16], is just
![]() $\infty $
itself. However,
$\infty $
itself. However,
![]() $[1/0]^{\flat } = 1/(1-q)$
.
$[1/0]^{\flat } = 1/(1-q)$
.
For other rationals
![]() $r/s$
, the two q-deformations can both be described via the action of a group
$r/s$
, the two q-deformations can both be described via the action of a group
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z}) \subset \operatorname {\mathrm {PSL}}_2(\mathbb {R})$
, which acts on
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z}) \subset \operatorname {\mathrm {PSL}}_2(\mathbb {R})$
, which acts on
![]() $\mathbb {R} \cup \{\infty \}$
by fractional linear transformations. The action of this group on the numbers
$\mathbb {R} \cup \{\infty \}$
by fractional linear transformations. The action of this group on the numbers
![]() $[r/s]^{\sharp }$
has been further explored in [Reference Leclere and Morier-Genoud12].
$[r/s]^{\sharp }$
has been further explored in [Reference Leclere and Morier-Genoud12].
We define the groups
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
and give the construction of the two q-deformations in parallel in Section 2.
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
and give the construction of the two q-deformations in parallel in Section 2.
1.2 A compactification of the space of stability conditions
The motivation for our two constructions of q-deformed rational numbers comes from homological algebra. To explain this, in Section 5, we associate to each positive real q a compactification of the space of Bridgeland stability conditions on
![]() $\mathcal {C}_{2}$
, the 2-Calabi–Yau (2-CY) triangulated category for the
$\mathcal {C}_{2}$
, the 2-Calabi–Yau (2-CY) triangulated category for the
![]() $A_2$
quiver. This compactification is a generalisation of a construction of [Reference Bapat, Deopurkar and Licata2], which corresponds to the case
$A_2$
quiver. This compactification is a generalisation of a construction of [Reference Bapat, Deopurkar and Licata2], which corresponds to the case
![]() $q=1$
, and proceeds by embedding the space of stability conditions into an infinite dimensional projective space, and taking the closure there. We set
$q=1$
, and proceeds by embedding the space of stability conditions into an infinite dimensional projective space, and taking the closure there. We set
![]() $M_q$
to be the image of the space of stability conditions under this embedding,
$M_q$
to be the image of the space of stability conditions under this embedding,
![]() $\overline {M_q}$
to be its closure and
$\overline {M_q}$
to be its closure and
![]() $\partial \overline {M_q}$
to be
$\partial \overline {M_q}$
to be
![]() $\overline {M_q} \backslash M_q$
. In the construction, the ambient projective space is independent of q, but the embedding itself depends on q.
$\overline {M_q} \backslash M_q$
. In the construction, the ambient projective space is independent of q, but the embedding itself depends on q.
When
![]() $q=1$
, the spaces involved can be identified with basic objects of hyperbolic geometry: the space of stability conditions
$q=1$
, the spaces involved can be identified with basic objects of hyperbolic geometry: the space of stability conditions
![]() $\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
can be identified with the upper half plane
$\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
can be identified with the upper half plane
![]() $\mathbb {H}^2$
(homeomorphic to the open disk), and the compactification is then the closed disk
$\mathbb {H}^2$
(homeomorphic to the open disk), and the compactification is then the closed disk
![]() $\mathbb {H}^2 \cup \mathbb {R} \cup \{\infty \}$
. The points of the boundary do not correspond to stability conditions, but they can be regarded as translation-invariant metrics on the category
$\mathbb {H}^2 \cup \mathbb {R} \cup \{\infty \}$
. The points of the boundary do not correspond to stability conditions, but they can be regarded as translation-invariant metrics on the category
![]() $\mathcal {C}_2$
. Moreover, there is a canonical bijection between the spherical objects of
$\mathcal {C}_2$
. Moreover, there is a canonical bijection between the spherical objects of
![]() $\mathcal {C}_2$
up to shift and the rationals
$\mathcal {C}_2$
up to shift and the rationals
![]() $\mathbb {Q}\cup \{\infty \} \subset \mathbb {R}\cup \{\infty \}$
. It is a theorem of Rouquier–Zimmermann [Reference Rouquier and Zimmermann17] that this bijection intertwines the braid group action on the spherical objects with the
$\mathbb {Q}\cup \{\infty \} \subset \mathbb {R}\cup \{\infty \}$
. It is a theorem of Rouquier–Zimmermann [Reference Rouquier and Zimmermann17] that this bijection intertwines the braid group action on the spherical objects with the
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
action on
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
action on
![]() $\mathbb {Q}\cup \{\infty \}$
. Details about this construction may be found in [Reference Bapat, Deopurkar and Licata2] and references therein.
$\mathbb {Q}\cup \{\infty \}$
. Details about this construction may be found in [Reference Bapat, Deopurkar and Licata2] and references therein.
One of the main goals of this paper is to establish analogues of this result for the case
![]() $q\ne 1$
. When we vary q, the space
$q\ne 1$
. When we vary q, the space
![]() $M_q$
remains an open disk, but something interesting happens at the boundary: each spherical object in the category corresponds not to a rational point, but rather to an entire interval in
$M_q$
remains an open disk, but something interesting happens at the boundary: each spherical object in the category corresponds not to a rational point, but rather to an entire interval in
![]() $\partial \overline {M}_{q}$
. We elaborate on this statement in Section 4.4, by associating two projectivised linear functionals to each spherical object X. These functionals, called
$\partial \overline {M}_{q}$
. We elaborate on this statement in Section 4.4, by associating two projectivised linear functionals to each spherical object X. These functionals, called
![]() $\overline {\hom }_{q}(X,\cdotp )$
and
$\overline {\hom }_{q}(X,\cdotp )$
and
![]() $\operatorname {\mathrm {occ}}_{q}(X,\cdotp )$
, each map the set of spherical objects to
$\operatorname {\mathrm {occ}}_{q}(X,\cdotp )$
, each map the set of spherical objects to
![]() $\mathbb {R}$
. The former sends Y to the Laurent polynomial whose
$\mathbb {R}$
. The former sends Y to the Laurent polynomial whose
![]() $q^{k}$
-coefficient is the number of degree-k morphisms from X to Y. The definition of
$q^{k}$
-coefficient is the number of degree-k morphisms from X to Y. The definition of
![]() $\operatorname {\mathrm {occ}}_{q}(X, \cdotp )$
is a little more involved but is also intrinsically well-motivated. At
$\operatorname {\mathrm {occ}}_{q}(X, \cdotp )$
is a little more involved but is also intrinsically well-motivated. At
![]() $q=1$
, these two functionals agree and lie on the boundary, coinciding with the rational point in
$q=1$
, these two functionals agree and lie on the boundary, coinciding with the rational point in
![]() $\mathbb {R} \cup \{\infty \}$
corresponding to the spherical object X. When
$\mathbb {R} \cup \{\infty \}$
corresponding to the spherical object X. When
![]() $q \neq 1$
, they are distinct functionals, and the entire closed interval of convex combinations of the two functionals lies on the boundary. We call this interval
$q \neq 1$
, they are distinct functionals, and the entire closed interval of convex combinations of the two functionals lies on the boundary. We call this interval
![]() $I_{q,X}$
. We summarise these statements in the following theorem.
$I_{q,X}$
. We summarise these statements in the following theorem.
Theorem 1.1.
-
1. For all
 $q\in (0,\infty )$
, the space of stability conditions maps homeomorphically onto
$q\in (0,\infty )$
, the space of stability conditions maps homeomorphically onto
 ${M}_{q}$
, which is in turn homeomorphic to an open disk.
${M}_{q}$
, which is in turn homeomorphic to an open disk. -
2. The boundary of
 $\overline {M_q}$
is
$\overline {M_q}$
is
 $\partial \overline {M}_{q}$
and is homeomorphic to
$\partial \overline {M}_{q}$
and is homeomorphic to
 $\mathbb {R} \cup \{\infty \}$
.
$\mathbb {R} \cup \{\infty \}$
. -
3. The union of the intervals
 $I_{q,X}$
, as X ranges over the spherical objects of
$I_{q,X}$
, as X ranges over the spherical objects of
 $\mathcal {C}_2$
, is a dense subset of the boundary
$\mathcal {C}_2$
, is a dense subset of the boundary
 $\partial \overline {M}_q$
.
$\partial \overline {M}_q$
.
Further, we conjecture that
![]() $\overline {M}_{q}$
is homeomorphic to a closed disk. We prove this theorem in Section 5. The main tool used in the proof is a finite state automaton known as a Harder–Narasimhan automaton or HN automaton, introduced in [Reference Bapat, Deopurkar and Licata2]. This automaton controls how the HN filtration of an object in the
$\overline {M}_{q}$
is homeomorphic to a closed disk. We prove this theorem in Section 5. The main tool used in the proof is a finite state automaton known as a Harder–Narasimhan automaton or HN automaton, introduced in [Reference Bapat, Deopurkar and Licata2]. This automaton controls how the HN filtration of an object in the
![]() $A_2$
category transforms when acted on by a braid. (This automaton is also of use when
$A_2$
category transforms when acted on by a braid. (This automaton is also of use when
![]() $q=1$
, where it allows for a simpler proof of Rouquier–Zimmermann’s original result.)
$q=1$
, where it allows for a simpler proof of Rouquier–Zimmermann’s original result.)
We expect the role of HN automata in the study of triangulated autoequivalence groups will be somewhat analogous to the role of Thurston’s train track automata in the study of mapping class groups. For 2-CY catgories, such automata have been constructed in type
![]() $A_2$
and type
$A_2$
and type
![]() $\widehat {A}_1$
in [Reference Bapat, Deopurkar and Licata2], and in the Ph.D. thesis of Edmund Heng in all other rank 2 Coxeter types [Reference Heng6]. Constructing HN automata in higher rank examples and exploiting them to study stability conditions and autoequivalence groups is an important open problem. We give the definition of HN automata in Section 3.
$\widehat {A}_1$
in [Reference Bapat, Deopurkar and Licata2], and in the Ph.D. thesis of Edmund Heng in all other rank 2 Coxeter types [Reference Heng6]. Constructing HN automata in higher rank examples and exploiting them to study stability conditions and autoequivalence groups is an important open problem. We give the definition of HN automata in Section 3.
1.3 Relationship to the q-rational numbers
Recall that at
![]() $q = 1$
, the correspondence of spherical objects to rational numbers intertwines the braid group action on the spherical objects with the
$q = 1$
, the correspondence of spherical objects to rational numbers intertwines the braid group action on the spherical objects with the
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
action on
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
action on
![]() $\mathbb {R}\cup \{\infty \}$
. The bulk of Section 4 is devoted to the q-analogue of this correspondence, where the group
$\mathbb {R}\cup \{\infty \}$
. The bulk of Section 4 is devoted to the q-analogue of this correspondence, where the group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
is replaced by the group
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
is replaced by the group
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
. We prove the following result (see Theorems 4.7 and 4.8 for the precise statements).
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
. We prove the following result (see Theorems 4.7 and 4.8 for the precise statements).
Theorem 1.2. Consider assignments
 $$\begin{align*}X \mapsto (-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_q(P_2,X)}{\operatorname{\mathrm{occ}}_q(P_1,X)} \quad\text{and}\quad X \mapsto q^{-1}(-q)^{\epsilon}\frac{\overline{\hom}_q(X,P_2)}{\overline{\hom}_q(X,P_1)},\end{align*}$$
$$\begin{align*}X \mapsto (-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_q(P_2,X)}{\operatorname{\mathrm{occ}}_q(P_1,X)} \quad\text{and}\quad X \mapsto q^{-1}(-q)^{\epsilon}\frac{\overline{\hom}_q(X,P_2)}{\overline{\hom}_q(X,P_1)},\end{align*}$$
where
![]() $\epsilon $
is either
$\epsilon $
is either
![]() $0$
or
$0$
or
![]() $1$
depending on X. Each of these assignments intertwines the
$1$
depending on X. Each of these assignments intertwines the
![]() $B_3$
action on the spherical objects of
$B_3$
action on the spherical objects of
![]() $\mathcal {C}_2$
with the
$\mathcal {C}_2$
with the
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
action on
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
action on
![]() $\mathbb {R}\cup \{\infty \}$
.
$\mathbb {R}\cup \{\infty \}$
.
In fact, the first of the two assignments above recovers the q-rational numbers of [Reference Morier-Genoud and Ovsienko16, Reference Morier-Genoud and Ovsienko15].
Theorem 1.3. Let X be a spherical object of
![]() $\mathcal {C}_2$
corresponding to the rational number
$\mathcal {C}_2$
corresponding to the rational number
![]() $r/s$
. The ratio
$r/s$
. The ratio
 $$\begin{align*}(-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_q(P_2,X)}{\operatorname{\mathrm{occ}}_q(P_1,X)}\end{align*}$$
$$\begin{align*}(-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_q(P_2,X)}{\operatorname{\mathrm{occ}}_q(P_1,X)}\end{align*}$$
is the q-deformation
![]() $[r/s]_{q}^{\sharp }$
in the sense of Morier-Genoud–Ovsienko [Reference Morier-Genoud and Ovsienko16, Reference Morier-Genoud and Ovsienko15].
$[r/s]_{q}^{\sharp }$
in the sense of Morier-Genoud–Ovsienko [Reference Morier-Genoud and Ovsienko16, Reference Morier-Genoud and Ovsienko15].
This result suggests that the corresponding ratio of
![]() $\overline {\hom }_q$
functionals
$\overline {\hom }_q$
functionals
 $$\begin{align*}q^{-1}(-q)^{\epsilon}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*}$$
$$\begin{align*}q^{-1}(-q)^{\epsilon}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*}$$
should be thought of as another q-deformation of the corresponding rational number; it is in fact the alternative q-deformation
![]() $[r/s]_{q}^{\flat }$
mentioned above. In Section 2, we give an elementary parallel account of both of these q-deformations, and Theorems 4.7 and 4.8 give precise relationships between the q-deformations and homological algebra.
$[r/s]_{q}^{\flat }$
mentioned above. In Section 2, we give an elementary parallel account of both of these q-deformations, and Theorems 4.7 and 4.8 give precise relationships between the q-deformations and homological algebra.
1.4 The Jones polynomial of rational knots
In [Reference Morier-Genoud and Ovsienko16, Appendix A], Morier-Genoud and Ovsienko relate the q-deformed rational numbers to the Jones polynomial of rational (two-bridge) knots. In particular, they prove that the normalised Jones polynomial is equal to
![]() $q\mathcal {R}(q)+(1-q)\mathcal {S}(q)$
, where
$q\mathcal {R}(q)+(1-q)\mathcal {S}(q)$
, where
![]() $[r/s]^{\sharp }_{q} = \mathcal {R}(q)/\mathcal {S}(q)$
. In our Appendix A, we prove an analogous result involving our new q-deformed rational number
$[r/s]^{\sharp }_{q} = \mathcal {R}(q)/\mathcal {S}(q)$
. In our Appendix A, we prove an analogous result involving our new q-deformed rational number
![]() $[r/s]^{\flat }_{q}$
: the numerator of
$[r/s]^{\flat }_{q}$
: the numerator of
![]() $[r/s]^{\flat }_{q}$
is equal to the Jones polynomial of the corresponding rational knot (up to the signs of the coefficients).
$[r/s]^{\flat }_{q}$
is equal to the Jones polynomial of the corresponding rational knot (up to the signs of the coefficients).
2 q-deformed rational numbers
In this section, we present two different q-deformations of the set
![]() $\mathbb {Q}\cup \{\infty \}$
, one of which is exactly the q-deformed rational numbers of [Reference Morier-Genoud and Ovsienko16]. We begin by defining the two q-deformations via continued fraction expansions. Although the definitions may appear unmotivated at first, the remainder of the section provides several interpretations of the two deformations that also serve as motivation. Throughout this paper, a rational number is considered to be any element of
$\mathbb {Q}\cup \{\infty \}$
, one of which is exactly the q-deformed rational numbers of [Reference Morier-Genoud and Ovsienko16]. We begin by defining the two q-deformations via continued fraction expansions. Although the definitions may appear unmotivated at first, the remainder of the section provides several interpretations of the two deformations that also serve as motivation. Throughout this paper, a rational number is considered to be any element of
![]() $\mathbb {Q}\cup \{\infty \}$
. Also throughout this paper, we treat the case
$\mathbb {Q}\cup \{\infty \}$
. Also throughout this paper, we treat the case
![]() $0<q \leq 1$
. The case
$0<q \leq 1$
. The case
![]() $1\leq q< \infty $
is symmetric, and, up to sign, all of our results are preserved under this symmetry.
$1\leq q< \infty $
is symmetric, and, up to sign, all of our results are preserved under this symmetry.
2.1 Left and right q-deformed rational numbers
Recall that every nonzero rational number
![]() $r/s$
has a unique even continued fraction expression
$r/s$
has a unique even continued fraction expression
![]() $[a_{1}, \ldots ,a_{2n}]$
, where
$[a_{1}, \ldots ,a_{2n}]$
, where
 $$ \begin{align*}\frac{r}{s}=a_{1}+\cfrac{1}{a_{2}+\cfrac{1}{a_{3}+\cfrac{1}{\cfrac{\ddots}{a_{2n-1}+\cfrac{1}{a_{2n}}}}}},\end{align*} $$
$$ \begin{align*}\frac{r}{s}=a_{1}+\cfrac{1}{a_{2}+\cfrac{1}{a_{3}+\cfrac{1}{\cfrac{\ddots}{a_{2n-1}+\cfrac{1}{a_{2n}}}}}},\end{align*} $$
and either
![]() $a_{1} \in \mathbb {N}$
and
$a_{1} \in \mathbb {N}$
and
![]() $a_{2}, \ldots , a_{2n} \in \mathbb {N}\setminus \{0\}$
, or
$a_{2}, \ldots , a_{2n} \in \mathbb {N}\setminus \{0\}$
, or
![]() $-a_{1} \in \mathbb {N}$
and
$-a_{1} \in \mathbb {N}$
and
![]() $-a_{2}, \ldots ,-a_{2n} \in \mathbb {N}\setminus \{0\}$
. The continued fraction expansion of 0 is
$-a_{2}, \ldots ,-a_{2n} \in \mathbb {N}\setminus \{0\}$
. The continued fraction expansion of 0 is
![]() $[-1,1]$
. The continued fraction expansion of
$[-1,1]$
. The continued fraction expansion of
![]() $\infty $
is the empty expansion
$\infty $
is the empty expansion
![]() $[\,]$
.
$[\,]$
.
Remark 2.1. The convention for continued fractions that we have chosen here is slightly nonstandard. However, we have the following pleasing dichotomy under this convention:
-
1. strictly positive rational numbers only contain nonnegative numbers in their continued fraction expansions;
-
2. strictly negative rational numbers only contain nonpositive numbers in their continued fraction expansions.
The points 0 and
![]() $\infty $
are both negative and positive, and thus exceptional. The choice of which corresponds to the empty expansion is equivalent to the choice between odd and even continued fraction expansions. The odd continued fraction expansion of 0 is
$\infty $
are both negative and positive, and thus exceptional. The choice of which corresponds to the empty expansion is equivalent to the choice between odd and even continued fraction expansions. The odd continued fraction expansion of 0 is
![]() $[\,]$
, and that of
$[\,]$
, and that of
![]() $\infty $
is
$\infty $
is
![]() $[0,1,-1]$
. For even continued fractions,
$[0,1,-1]$
. For even continued fractions,
![]() $\infty $
is the ‘basepoint’ in Proposition 2.2; for odd continued fractions, it is 0.
$\infty $
is the ‘basepoint’ in Proposition 2.2; for odd continued fractions, it is 0.
The continued fraction expansion is related to the modular group
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
action on
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
action on
![]() $\mathbb {Q}\cup \{\infty \}$
. Recall that
$\mathbb {Q}\cup \{\infty \}$
. Recall that
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
is the quotient of the group of
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
is the quotient of the group of
![]() $2\times 2$
real invertible matrices by scalar matrices. The group
$2\times 2$
real invertible matrices by scalar matrices. The group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
is the subgroup of
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
is the subgroup of
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
generated by
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
generated by
 $$ \begin{align*} \sigma_{1}:=\begin{bmatrix} 1& -1 \\ 0 & 1\end{bmatrix}, \quad \sigma_{2}:= \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \sigma_{1}:=\begin{bmatrix} 1& -1 \\ 0 & 1\end{bmatrix}, \quad \sigma_{2}:= \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}. \end{align*} $$
The group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
acts on each of the sets
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
acts on each of the sets
by fractional linear transformations:
 $$ \begin{align}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot z=\frac{az+b}{cz+d}. \end{align} $$
$$ \begin{align}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot z=\frac{az+b}{cz+d}. \end{align} $$
The modular group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
also preserves, and is transitive on,
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
also preserves, and is transitive on,
![]() $\mathbb {Q} \cup \{\infty \}$
. The following is easy to check.
$\mathbb {Q} \cup \{\infty \}$
. The following is easy to check.
Proposition 2.2. Let r/s be a rational number. Suppose that r/s has an even continued fraction expansion [a 1, …, a 2n ]. Then
under the usual action of PSL2(ℤ) on ℚ ∪{∞}.
In order to obtain q-deformations of the rationals, we first define a family of discrete subgroups of
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
indexed by q, which deform the modular group
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
indexed by q, which deform the modular group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
. We then define the q-deformed rational using the action of the q-indexed subgroup, analogously to Proposition 2.2. This q-deformation of the modular group, and its relation to the q-rationals, was first studied in [Reference Leclere and Morier-Genoud12].
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
. We then define the q-deformed rational using the action of the q-indexed subgroup, analogously to Proposition 2.2. This q-deformation of the modular group, and its relation to the q-rationals, was first studied in [Reference Leclere and Morier-Genoud12].
Definition 2.3 [Reference Leclere and Morier-Genoud12, Section 3.2].
Set
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
to be the subgroup of
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
to be the subgroup of
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
generated by
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
generated by
 $$\begin{align*}\sigma_{1,q}:= \begin{bmatrix} q^{-1} & - q^{-1} \\ 0 & 1 \end{bmatrix}, \quad \sigma_{2,q}:=\begin{bmatrix} 1 & 0 \\ 1 & q^{-1} \end{bmatrix}.\end{align*}$$
$$\begin{align*}\sigma_{1,q}:= \begin{bmatrix} q^{-1} & - q^{-1} \\ 0 & 1 \end{bmatrix}, \quad \sigma_{2,q}:=\begin{bmatrix} 1 & 0 \\ 1 & q^{-1} \end{bmatrix}.\end{align*}$$
At
![]() $q = 1$
, the group
$q = 1$
, the group
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
is simply
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
is simply
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
. Recall the three-strand Artin braid group:
$\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
. Recall the three-strand Artin braid group:
The following is easy to check.
Proposition 2.4. The assignment
gives a homomorphism from
![]() $B_3$
to
$B_3$
to
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
.
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
.
Our definitions of the q-deformed rational numbers are motivated by Proposition 2.2 and use the homomorphism from
![]() $B_3 \to \operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
described above. We first set up the following notation.
$B_3 \to \operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
described above. We first set up the following notation.
Definition 2.5. Given an even continued fraction expansion
as above, define the braid corresponding to a as the following element of B 3:
For any q ∈ ℝ, denote by β a, q the image of β a in PSL2, q (ℤ).
Now we are in a position to define the q-deformed rational numbers (the second part is equivalent to [Reference Leclere and Morier-Genoud12, Proposition 3.2]).
Definition 2.6 (Left and right q-deformed rationals).
Let
![]() $r/s \in \mathbb {Q}\cup \{\infty \}$
with continued fraction expansion
$r/s \in \mathbb {Q}\cup \{\infty \}$
with continued fraction expansion
![]() $\mathbf {a}$
.
$\mathbf {a}$
.
-
1. The left q-deformed rational number corresponding to
 $r/s$
is
$r/s$
is  $$\begin{align*}\left[\frac{r}{s}\right]^{\flat}_q = \beta_{\mathbf{a},q}\left(\frac{1}{1-q}\right).\end{align*}$$
$$\begin{align*}\left[\frac{r}{s}\right]^{\flat}_q = \beta_{\mathbf{a},q}\left(\frac{1}{1-q}\right).\end{align*}$$
-
2. The right q-deformed rational number corresponding to
 $r/s$
is
$r/s$
is  $$\begin{align*}\left[\frac{r}{s}\right]^{\sharp}_q = \beta_{\mathbf{a},q}\left(\infty\right).\end{align*}$$
$$\begin{align*}\left[\frac{r}{s}\right]^{\sharp}_q = \beta_{\mathbf{a},q}\left(\infty\right).\end{align*}$$
At
![]() $q = 1$
, the left and right deformed rationals coincide and, by Proposition 2.2, are both equal to
$q = 1$
, the left and right deformed rationals coincide and, by Proposition 2.2, are both equal to
![]() $r/s$
.
$r/s$
.
Definition 2.7. Following [Reference Morier-Genoud and Ovsienko16], we fix the following notation for the rational functions associated to the left and right q-deformed rational numbers:
 $$\begin{align*}\left[\frac{r}{s}\right]_{q}^{\flat}=\frac{\mathcal{R}^{\flat}(q)}{\mathcal{S}^{\flat}(q)},\quad \left[\frac{r}{s}\right]_{q}^{\sharp}=\frac{\mathcal{R}^{\sharp}(q)}{\mathcal{S}^{\sharp}(q)},\end{align*}$$
$$\begin{align*}\left[\frac{r}{s}\right]_{q}^{\flat}=\frac{\mathcal{R}^{\flat}(q)}{\mathcal{S}^{\flat}(q)},\quad \left[\frac{r}{s}\right]_{q}^{\sharp}=\frac{\mathcal{R}^{\sharp}(q)}{\mathcal{S}^{\sharp}(q)},\end{align*}$$
where the polynomials in the numerator and denominator are normalised so that if
![]() $r/s>0$
(resp.
$r/s>0$
(resp.
![]() $r/s<0$
), the denominator has the lowest (resp. highest) degree term equal to 1. If
$r/s<0$
), the denominator has the lowest (resp. highest) degree term equal to 1. If
![]() $r/s=0$
, we set
$r/s=0$
, we set
If
![]() $r/s=\infty $
, we set
$r/s=\infty $
, we set
Remark 2.8. Note that
![]() $\mathcal {R}^{\flat }(q)$
,
$\mathcal {R}^{\flat }(q)$
,
![]() $\mathcal {S}^{\flat }(q)$
,
$\mathcal {S}^{\flat }(q)$
,
![]() $\mathcal {R}^{\sharp }(q)$
and
$\mathcal {R}^{\sharp }(q)$
and
![]() $\mathcal {S}^{\sharp }(q)$
depend on both r and s.
$\mathcal {S}^{\sharp }(q)$
depend on both r and s.
Example 2.9. Here are some simple examples of q-deformed rational numbers (cf. [Reference Morier-Genoud and Ovsienko16, Example 1.2]).
 $$ \begin{align*} \left[\frac{1}{2}\right]_{q}^{\flat} &=\frac{q^{2}}{1+q^{2}}, & \left[\frac{1}{2}\right]_{q}^{\sharp} &=\frac{q}{1+q},\\ \left[\frac{3}{2}\right]_{q}^{\flat} &=\frac{1+q^{2}+q^{3}}{1+q^{2}}, & \left[\frac{3}{2}\right]_{q}^{\sharp} &=\frac{1+q+q^{2}}{1+q},\\ \left[\frac{5}{2}\right]_{q}^{\flat} &=\frac{1+q+q^{2}+q^{3}+q^{4}}{1+q^{2}}, & \left[\frac{5}{2}\right]_{q}^{\sharp} &=\frac{1+2q+q^{2}+q^{3}}{1+q},\\ \left[\frac{5}{3}\right]_{q}^{\flat} &=\frac{1+q+q^{2}+q^{3}+q^{4}}{1+q+q^{3}}, & \left[\frac{5}{3}\right]_{q}^{\sharp} &=\frac{1+q+2q^{2}+q^{3}}{1+q+q^{2}},\\ \left[\frac{8}{3}\right]_{q}^{\flat} &=\frac{1+2q+q^{2}+2q^{3}+q^{4}+q^{5}}{1+q+q^{3}}, & \left[\frac{8}{3}\right]_{q}^{\sharp} &=\frac{1+2q+2q^{2}+2q^{3}+q^{4}}{1+q+q^{2}}.\\ \end{align*} $$
$$ \begin{align*} \left[\frac{1}{2}\right]_{q}^{\flat} &=\frac{q^{2}}{1+q^{2}}, & \left[\frac{1}{2}\right]_{q}^{\sharp} &=\frac{q}{1+q},\\ \left[\frac{3}{2}\right]_{q}^{\flat} &=\frac{1+q^{2}+q^{3}}{1+q^{2}}, & \left[\frac{3}{2}\right]_{q}^{\sharp} &=\frac{1+q+q^{2}}{1+q},\\ \left[\frac{5}{2}\right]_{q}^{\flat} &=\frac{1+q+q^{2}+q^{3}+q^{4}}{1+q^{2}}, & \left[\frac{5}{2}\right]_{q}^{\sharp} &=\frac{1+2q+q^{2}+q^{3}}{1+q},\\ \left[\frac{5}{3}\right]_{q}^{\flat} &=\frac{1+q+q^{2}+q^{3}+q^{4}}{1+q+q^{3}}, & \left[\frac{5}{3}\right]_{q}^{\sharp} &=\frac{1+q+2q^{2}+q^{3}}{1+q+q^{2}},\\ \left[\frac{8}{3}\right]_{q}^{\flat} &=\frac{1+2q+q^{2}+2q^{3}+q^{4}+q^{5}}{1+q+q^{3}}, & \left[\frac{8}{3}\right]_{q}^{\sharp} &=\frac{1+2q+2q^{2}+2q^{3}+q^{4}}{1+q+q^{2}}.\\ \end{align*} $$
By the results of [Reference Morier-Genoud and Ovsienko16, Section 2.6], it is clear that our right q-deformed rational numbers are the same as the q-rational numbers considered in [Reference Morier-Genoud and Ovsienko16]. And by [Reference Leclere and Morier-Genoud12, Theorem 4], this definition does not depend on the particular choice of continued fraction representation. In the next section, we motivate our definition of left q-deformed rational numbers.
2.2 Motivation via the q-Farey tessellation
In this section, we recall a q-deformation of the classical Farey tessellation of the hyperbolic plane, originally considered in [Reference Morier-Genoud and Ovsienko16]. We first recall the classical Farey tessellation. The hyperbolic plane has an upper half-plane model:
which embeds naturally into
![]() $\mathbb {C} \cup \{\infty \}$
. The group
$\mathbb {C} \cup \{\infty \}$
. The group
![]() $\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
, which acts on
$\operatorname {\mathrm {PSL}}_2(\mathbb {R})$
, which acts on
![]() $\mathbb {C} \cup \{\infty \}$
by fractional linear transformations, preserves the hyperbolic plane
$\mathbb {C} \cup \{\infty \}$
by fractional linear transformations, preserves the hyperbolic plane
![]() $\mathbb {H}$
and acts on it by hyperbolic isometries.
$\mathbb {H}$
and acts on it by hyperbolic isometries.
The hyperbolic plane admits a tessellation by ideal triangles according to the following iterative construction. We begin with an ‘initial geodesic’ E, namely the straight vertical line from
![]() $0$
to
$0$
to
![]() $\infty $
. Starting with E, we complete every geodesic in the tessellation to a triangle according to the following rule, called the Farey rule. By induction, every geodesic in the tessellation has rational vertices
$\infty $
. Starting with E, we complete every geodesic in the tessellation to a triangle according to the following rule, called the Farey rule. By induction, every geodesic in the tessellation has rational vertices
![]() $r/s$
and
$r/s$
and
![]() $r'/s'$
(the integers
$r'/s'$
(the integers
![]() $r,s,r',s'$
are uniquely determined by construction). We add a geodesic from
$r,s,r',s'$
are uniquely determined by construction). We add a geodesic from
![]() $r/s$
to
$r/s$
to
![]() $(r+r')/(s+s')$
and a geodesic from
$(r+r')/(s+s')$
and a geodesic from
![]() $(r+r')/(s+s')$
to
$(r+r')/(s+s')$
to
![]() $r'/s'$
(see Fig. 1). The ‘positive half’ of the hyperbolic plane, those
$r'/s'$
(see Fig. 1). The ‘positive half’ of the hyperbolic plane, those
![]() $z \in \mathbb {H}$
such that
$z \in \mathbb {H}$
such that
![]() $0\leq \Re (z) < \infty $
, is covered by applying the rule to the initial geodesic E with its vertices viewed as the fractions
$0\leq \Re (z) < \infty $
, is covered by applying the rule to the initial geodesic E with its vertices viewed as the fractions
![]() $0/1$
and
$0/1$
and
![]() $1/0$
. The ‘negative half’ is obtained by applying the rule to E with its vertices viewed as the fractions
$1/0$
. The ‘negative half’ is obtained by applying the rule to E with its vertices viewed as the fractions
![]() $0/1$
and
$0/1$
and
![]() $-1/0$
. We call the resulting tessellation the Farey tessellation of the hyperbolic plane. The set of vertices of the Farey tessellation is exactly
$-1/0$
. We call the resulting tessellation the Farey tessellation of the hyperbolic plane. The set of vertices of the Farey tessellation is exactly
![]() $\mathbb {Q} \cup \{\infty \}$
. Moreover, the Farey tessellation is preserved by the
$\mathbb {Q} \cup \{\infty \}$
. Moreover, the Farey tessellation is preserved by the
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action described above (that is, the
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action described above (that is, the
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action sends triangles to triangles), and the
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action sends triangles to triangles), and the
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-orbit of any Farey triangle is the entire hyperbolic plane.
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-orbit of any Farey triangle is the entire hyperbolic plane.

Figure 1 A standard Farey triangle.
Morier-Genoud and Ovsienko introduced a q-deformed Farey rule, which generates a tessellation of a subset of
![]() $\mathbb {H}$
. As with the regular Farey rule, we begin with a geodesic E between
$\mathbb {H}$
. As with the regular Farey rule, we begin with a geodesic E between
![]() $0$
and
$0$
and
![]() $\infty $
, but it is now assigned a label
$\infty $
, but it is now assigned a label
![]() $q^{-1}$
. We then extend every geodesic in the tessellation, with vertices
$q^{-1}$
. We then extend every geodesic in the tessellation, with vertices
![]() $\mathcal {R}(q)/\mathcal {S}(q)$
and
$\mathcal {R}(q)/\mathcal {S}(q)$
and
![]() $\mathcal {R}'(q)/\mathcal {S}'(q)$
(the vertices are now rational functions evaluated at q), to a triangle according to Fig. 2 (see [Reference Morier-Genoud and Ovsienko16, Definition 2.9]).
$\mathcal {R}'(q)/\mathcal {S}'(q)$
(the vertices are now rational functions evaluated at q), to a triangle according to Fig. 2 (see [Reference Morier-Genoud and Ovsienko16, Definition 2.9]).

Figure 2 A q-deformed Farey triangle.
For the positive half, interpret the vertices of E as the fractions
![]() $0/1$
and
$0/1$
and
![]() $1/0$
, and then continue according to Fig. 2. For the negative half, interpret the vertices of E as
$1/0$
, and then continue according to Fig. 2. For the negative half, interpret the vertices of E as
![]() $0/q$
and
$0/q$
and
![]() $-1/0$
. The bottom left edge of any triangle is always labelled
$-1/0$
. The bottom left edge of any triangle is always labelled
![]() $1$
, and we iteratively deduce labels for all other edges. The set of vertices of the q-deformed Farey tessellations is exactly the set of right q-deformed rational numbers
$1$
, and we iteratively deduce labels for all other edges. The set of vertices of the q-deformed Farey tessellations is exactly the set of right q-deformed rational numbers
![]() $[r/s]^{\sharp }_q$
. Fig. 3 depicts what the q-deformed Farey tessellations look like at two different values of q.
$[r/s]^{\sharp }_q$
. Fig. 3 depicts what the q-deformed Farey tessellations look like at two different values of q.

Figure 3 The deformed Farey tessellations at two values of q.
The action of
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
on
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
on
![]() $\mathbb {H}$
preserves q-deformed Farey triangles (since
$\mathbb {H}$
preserves q-deformed Farey triangles (since
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
is a subgroup of
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
is a subgroup of
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {R})$
, which preserves geodesics). Moreover,
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {R})$
, which preserves geodesics). Moreover,
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
acts on the q-deformed Farey tessellation exactly as
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
acts on the q-deformed Farey tessellation exactly as
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
acts on the classical Farey tessellation. More formally, let
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
acts on the classical Farey tessellation. More formally, let
![]() $\mathbb {T}$
denote the set of triangles in the Farey tessellation, and let
$\mathbb {T}$
denote the set of triangles in the Farey tessellation, and let
![]() $\mathbb {T}_{q}$
denote the set of q-deformed triangles. Since the
$\mathbb {T}_{q}$
denote the set of q-deformed triangles. Since the
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action preserves Farey triangles, there is an induced
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action preserves Farey triangles, there is an induced
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action on
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
-action on
![]() $\mathbb {T}$
, and similarly, there is an induced
$\mathbb {T}$
, and similarly, there is an induced
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
-action on
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
-action on
![]() $\mathbb {T}_{q}$
. Let
$\mathbb {T}_{q}$
. Let
![]() $\psi \colon \operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z}) \to \operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
be the group homomorphism given by setting
$\psi \colon \operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z}) \to \operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
be the group homomorphism given by setting
![]() $q = 1$
, and let
$q = 1$
, and let
![]() $\phi \colon \mathbb {T}_q \to \mathbb {T}$
be induced from the map
$\phi \colon \mathbb {T}_q \to \mathbb {T}$
be induced from the map
![]() $\mathcal {R}(q)/\mathcal {S}(q) \mapsto \mathcal {R}(1)/\mathcal {S}(1)$
on the vertices. Then, for any
$\mathcal {R}(q)/\mathcal {S}(q) \mapsto \mathcal {R}(1)/\mathcal {S}(1)$
on the vertices. Then, for any
![]() ${\beta } \in \operatorname {\mathrm {PSL}}_{2, q}(\mathbb {Z})$
, we have the following commutative square, as can be proven by comparing the actions on the vertices of the respective tessellations.
${\beta } \in \operatorname {\mathrm {PSL}}_{2, q}(\mathbb {Z})$
, we have the following commutative square, as can be proven by comparing the actions on the vertices of the respective tessellations.

We can now describe how left q-rationals arise in the q-deformed Farey tessellation. Consider any rational
![]() $r/s$
. In the standard Farey tessellation,
$r/s$
. In the standard Farey tessellation,
![]() $r/s$
is the middle vertex of a unique triangle and the right (resp. left) vertex of an infinite sequence of triangles. In the notation of Fig. 4,
$r/s$
is the middle vertex of a unique triangle and the right (resp. left) vertex of an infinite sequence of triangles. In the notation of Fig. 4,
![]() $r/s$
is the right vertex of
$r/s$
is the right vertex of
![]() $T_{0},T_{1},\ldots $
and the left vertex of
$T_{0},T_{1},\ldots $
and the left vertex of
![]() $T_{0}^{'},T_{1}^{'},\ldots $
.
$T_{0}^{'},T_{1}^{'},\ldots $
.

Figure 4 A fraction in the standard Farey tessellation.
Assume for convenience that
![]() $0<r/s<\infty $
, and let
$0<r/s<\infty $
, and let
![]() $T_{A}$
denote the triangle with vertices
$T_{A}$
denote the triangle with vertices
![]() $0,1,\infty $
. If the continued fraction expansion of
$0,1,\infty $
. If the continued fraction expansion of
![]() $r/s$
is
$r/s$
is
![]() $\mathbf {a}$
, then
$\mathbf {a}$
, then
Similarly, letting
![]() ${\beta }_{\mathbf {a}}^{'}={\beta }_{\mathbf {a}}\sigma _{2}^{-1}\sigma _{1}^{-1}$
, we have
${\beta }_{\mathbf {a}}^{'}={\beta }_{\mathbf {a}}\sigma _{2}^{-1}\sigma _{1}^{-1}$
, we have
As suggested by Fig. 4, for any point
![]() $x \in T_{0}$
,
$x \in T_{0}$
,
and for any point
![]() $x' \in T_{0}^{'}$
,
$x' \in T_{0}^{'}$
,
So we can view the rational point
![]() $r/s$
in the boundary as the limit of the sequences of Farey triangles
$r/s$
in the boundary as the limit of the sequences of Farey triangles
![]() $(T_{n})_{n \in \mathbb {N}}, (T_{n}^{'})_{n \in \mathbb {N}}$
.
$(T_{n})_{n \in \mathbb {N}}, (T_{n}^{'})_{n \in \mathbb {N}}$
.
When we
![]() $q$
-deform the Farey tessellation, we obtain corresponding sequences of triangles
$q$
-deform the Farey tessellation, we obtain corresponding sequences of triangles
![]() $(T_{q,n})_{n \in \mathbb{N}}, (T_{q,n}^{'})_{n\in \mathbb{N}}$
. The rightmost vertex of the triangles
$(T_{q,n})_{n \in \mathbb{N}}, (T_{q,n}^{'})_{n\in \mathbb{N}}$
. The rightmost vertex of the triangles
![]() $(T_{q,n})_{n \in \mathbb{N}}$
and the leftmost vertex of the triangles
$(T_{q,n})_{n \in \mathbb{N}}$
and the leftmost vertex of the triangles
![]() $(T_{q,n}^{'})_{n\in \mathbb{N}}$
is the right
$(T_{q,n}^{'})_{n\in \mathbb{N}}$
is the right
![]() $q$
-deformed rational number
$q$
-deformed rational number
![]() $[r/s]^{\sharp}_q$
(see Fig. 5). Theorem 2.12 proves that the sequence of rightmost vertices of the triangles
$[r/s]^{\sharp}_q$
(see Fig. 5). Theorem 2.12 proves that the sequence of rightmost vertices of the triangles
![]() $T_{q,n}'$
(and therefore the sequence of triangles
$T_{q,n}'$
(and therefore the sequence of triangles
![]() $T_{q,n}'$
) limits to
$T_{q,n}'$
) limits to
![]() $[r/s]^{\sharp}_q$
. On the other hand, by Theorem 2.12, the sequence of leftmost vertices of the triangles
$[r/s]^{\sharp}_q$
. On the other hand, by Theorem 2.12, the sequence of leftmost vertices of the triangles
![]() $T_{q,n}$
limits to
$T_{q,n}$
limits to
![]() $[r/s]^{\flat}_q$
. It is not hard to check that the sequence of triangles
$[r/s]^{\flat}_q$
. It is not hard to check that the sequence of triangles
![]() $T_{q,n}$
limits to a geodesic, with endpoints on the boundary (see Fig. 5). We call this geodesic the q-deformed rational curve corresponding to
$T_{q,n}$
limits to a geodesic, with endpoints on the boundary (see Fig. 5). We call this geodesic the q-deformed rational curve corresponding to
![]() $r/s$
. The left q-rational corresponding to
$r/s$
. The left q-rational corresponding to
![]() $r/s$
is the left endpoint of a q-deformed rational curve, and the right q-rational corresponding to
$r/s$
is the left endpoint of a q-deformed rational curve, and the right q-rational corresponding to
![]() $r/s$
is the right endpoint of the same curve. We denote by
$r/s$
is the right endpoint of the same curve. We denote by
![]() $\mathbb {Q}_q$
the union of all of the q-deformed rational curves, together with their endpoints. This motivates our definition of left and right q-rationals. Namely, if
$\mathbb {Q}_q$
the union of all of the q-deformed rational curves, together with their endpoints. This motivates our definition of left and right q-rationals. Namely, if
![]() $T_{n} \xrightarrow {n \to \infty } r/s$
, then the corresponding q-deformed sequence of triangles
$T_{n} \xrightarrow {n \to \infty } r/s$
, then the corresponding q-deformed sequence of triangles
![]() $T_{n,q}$
limits to the geodesic with endpoints
$T_{n,q}$
limits to the geodesic with endpoints
![]() $[r/s]_{q}^{\flat }$
and
$[r/s]_{q}^{\flat }$
and
![]() $[r/s]_{q}^{\sharp }$
.
$[r/s]_{q}^{\sharp }$
.

Figure 5 The sequence of triangles
![]() $T_{n,q}$
converging to the q-deformed rational curve of
$T_{n,q}$
converging to the q-deformed rational curve of
![]() $r/s$
, shown as a dotted line.
$r/s$
, shown as a dotted line.
2.3 Alternate descriptions of the deformed rational numbers
The left and right q-deformed rational numbers admit several elegant intrinsic definitions. Recall the classical q-deformation of the integers, which we call the right q-deformation:
We introduce a corresponding left q-deformation of n:
 $$\begin{align*}[n]_{q}^{\flat}:=\frac{1-q^{n-1}+q^{n}-q^{n+1}}{1-q} = 1 + q + \cdots + q^{n-2} + q^n.\end{align*}$$
$$\begin{align*}[n]_{q}^{\flat}:=\frac{1-q^{n-1}+q^{n}-q^{n+1}}{1-q} = 1 + q + \cdots + q^{n-2} + q^n.\end{align*}$$
The following proposition gives equivalent definitions of the two q-deformations of the rational numbers and is easy to check. In fact, this is how the (right) q-deformed rational numbers were originally defined (see [Reference Morier-Genoud and Ovsienko16, Definition 1.1]).
Proposition 2.10. Let
![]() $r/s$
be a finite rational number with even continued fraction expansion
$r/s$
be a finite rational number with even continued fraction expansion
![]() $[a_{1}, \ldots ,a_{2n}]$
.
$[a_{1}, \ldots ,a_{2n}]$
.
-
1. The corresponding right q-deformed rational has the following formula.
 $$\begin{align*}\Big[\cfrac{r}{s}\Big]^{\sharp}_{q} = [a_{1}]^{\sharp}_{q}+\cfrac{q^{a_{1}}}{[a_{2}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{2}}}{[a_{3}]^{\sharp}_{q}+\cfrac{q^{a_{3}}}{[a_{4}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{4}}}{\cfrac{\ddots}{[a_{2n-1}]^{\sharp}_{q}+\cfrac{q^{a_{2n-1}}}{[a_{2n}]^{\sharp}_{q^{-1}}}}}}}}\end{align*}$$
$$\begin{align*}\Big[\cfrac{r}{s}\Big]^{\sharp}_{q} = [a_{1}]^{\sharp}_{q}+\cfrac{q^{a_{1}}}{[a_{2}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{2}}}{[a_{3}]^{\sharp}_{q}+\cfrac{q^{a_{3}}}{[a_{4}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{4}}}{\cfrac{\ddots}{[a_{2n-1}]^{\sharp}_{q}+\cfrac{q^{a_{2n-1}}}{[a_{2n}]^{\sharp}_{q^{-1}}}}}}}}\end{align*}$$
-
2. The corresponding left q-deformed rational has the following formula.
 $$\begin{align*}\Big[\cfrac{r}{s}\Big]_{q}^{\flat} =[a_{1}]^{\sharp}_{q}+\cfrac{q^{a_{1}}}{[a_{2}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{2}}}{\cfrac{\ddots}{[a_{2n-1}]^{\sharp}_{q}+\cfrac{q^{a_{2n-1}}}{[a_{2n}]_{q^{-1}}^{\flat}}}}}\end{align*}$$
$$\begin{align*}\Big[\cfrac{r}{s}\Big]_{q}^{\flat} =[a_{1}]^{\sharp}_{q}+\cfrac{q^{a_{1}}}{[a_{2}]^{\sharp}_{q^{-1}}+\cfrac{q^{-a_{2}}}{\cfrac{\ddots}{[a_{2n-1}]^{\sharp}_{q}+\cfrac{q^{a_{2n-1}}}{[a_{2n}]_{q^{-1}}^{\flat}}}}}\end{align*}$$
The continued fraction expansion of every q-deformed rational number induces an element of
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
analogous to that in Proposition 2.2. Right-multiplying this element by
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
analogous to that in Proposition 2.2. Right-multiplying this element by
![]() $\infty $
(for right q-rationals) or
$\infty $
(for right q-rationals) or
![]() $1/(1-q)$
(for left q-rationals) returns the original q-rational. The following proposition expresses this element of
$1/(1-q)$
(for left q-rationals) returns the original q-rational. The following proposition expresses this element of
![]() $\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
in terms of the numerators and denominators of the corresponding q-rationals. The second part of this proposition appears as [Reference Morier-Genoud and Ovsienko16, Proposition 4.3].
$\operatorname {\mathrm {PSL}}_{2,q}(\mathbb {Z})$
in terms of the numerators and denominators of the corresponding q-rationals. The second part of this proposition appears as [Reference Morier-Genoud and Ovsienko16, Proposition 4.3].
Proposition 2.11 (Matrix formula for q-rationals).
Consider any rational number
![]() $r/s$
with continued fraction expansion
$r/s$
with continued fraction expansion
![]() $\mathbf {a}=[a_{1},\ldots ,a_{2n}]$
. Let
$\mathbf {a}=[a_{1},\ldots ,a_{2n}]$
. Let
![]() $r'/s'$
be the rational number with continued fraction expansion
$r'/s'$
be the rational number with continued fraction expansion
![]() $[a_{1}, \ldots ,a_{2n-1}]$
.
$[a_{1}, \ldots ,a_{2n-1}]$
.
-
1. We have the following for left q-rationals.
 $$\begin{align*}q^{a_{2}+a_{4}+ \cdots +a_{2n-2}}{\beta}_{\mathbf{a},q} \begin{bmatrix}1 & 1-q^{-1} \\ 1-q&1 \end{bmatrix}= \begin{cases} \begin{bmatrix}q^{-a_{2n}}\mathcal{R}^{\flat}(q) & \mathcal{R}^{\flat\prime}(q) \\ q^{-a_{2n}}\mathcal{S}^{\flat}(q) & \mathcal{S}^{\flat\prime}(q) \end{bmatrix}, & \displaystyle 0\leq \frac{r}{s}<\infty,\\[3ex] \begin{bmatrix} q^{-a_{2n}+1}\mathcal{R}^{\flat}(q) & \mathcal{R}^{\flat\prime}(q) \\ q^{-a_{2n}+1}\mathcal{S}^{\flat}(q) & \mathcal{S}^{\flat\prime}(q) \end{bmatrix}, & \displaystyle \frac{r}{s}<0\text{ or } \frac{r}{s}=\infty. \end{cases}\end{align*}$$
$$\begin{align*}q^{a_{2}+a_{4}+ \cdots +a_{2n-2}}{\beta}_{\mathbf{a},q} \begin{bmatrix}1 & 1-q^{-1} \\ 1-q&1 \end{bmatrix}= \begin{cases} \begin{bmatrix}q^{-a_{2n}}\mathcal{R}^{\flat}(q) & \mathcal{R}^{\flat\prime}(q) \\ q^{-a_{2n}}\mathcal{S}^{\flat}(q) & \mathcal{S}^{\flat\prime}(q) \end{bmatrix}, & \displaystyle 0\leq \frac{r}{s}<\infty,\\[3ex] \begin{bmatrix} q^{-a_{2n}+1}\mathcal{R}^{\flat}(q) & \mathcal{R}^{\flat\prime}(q) \\ q^{-a_{2n}+1}\mathcal{S}^{\flat}(q) & \mathcal{S}^{\flat\prime}(q) \end{bmatrix}, & \displaystyle \frac{r}{s}<0\text{ or } \frac{r}{s}=\infty. \end{cases}\end{align*}$$
-
2. We have the following for right q-rationals.
 $$\begin{align*}q^{a_{2}+a_{4}+ \cdots +a_{2n}}{\beta}_{\mathbf{a},q}= \begin{cases} \begin{bmatrix}q\mathcal{R}^{\sharp}(q) & \mathcal{R}^{\sharp\prime}(q) \\ q\mathcal{S}^{\sharp}(q) & \mathcal{S}^{\sharp\prime}(q) \end{bmatrix},& \displaystyle 0\leq \frac{r}{s}<\infty,\\[3ex] \begin{bmatrix}\mathcal{R}^{\sharp}(q) & \mathcal{R}^{\sharp\prime}(q) \\ \mathcal{S}^{\sharp}(q) & \mathcal{S}^{\sharp\prime}(q) \end{bmatrix}, & \displaystyle\frac{r}{s}<0 \text{ or } \frac{r}{s}=\infty. \end{cases}\end{align*}$$
$$\begin{align*}q^{a_{2}+a_{4}+ \cdots +a_{2n}}{\beta}_{\mathbf{a},q}= \begin{cases} \begin{bmatrix}q\mathcal{R}^{\sharp}(q) & \mathcal{R}^{\sharp\prime}(q) \\ q\mathcal{S}^{\sharp}(q) & \mathcal{S}^{\sharp\prime}(q) \end{bmatrix},& \displaystyle 0\leq \frac{r}{s}<\infty,\\[3ex] \begin{bmatrix}\mathcal{R}^{\sharp}(q) & \mathcal{R}^{\sharp\prime}(q) \\ \mathcal{S}^{\sharp}(q) & \mathcal{S}^{\sharp\prime}(q) \end{bmatrix}, & \displaystyle\frac{r}{s}<0 \text{ or } \frac{r}{s}=\infty. \end{cases}\end{align*}$$
2.4 Limits of q-deformed rational numbers
The following theorem partially formalises the description of q-deformed rational numbers depicted in Fig. 4 and Fig. 5. The vertices of the q-Farey tessellation are the right q-deformed rationals, while the left q-deformed rational numbers arise as limits of sequences of right q-deformed rationals. The same phenomenon is described in [Reference Morier-Genoud and Ovsienko15], in terms of Taylor series; see especially Theorem 1 and Remark 3.2. The proof owes its technique to the proofs in that paper.
Theorem 2.12 (Limits of q-rationals).
Suppose
![]() $q<1$
. Consider any convergent sequence of rational numbers
$q<1$
. Consider any convergent sequence of rational numbers
![]() $(r_{m}/s_{m})_{m \in \mathbb {N}} \in \mathbb {Q}^{\mathbb {N}}$
.
$(r_{m}/s_{m})_{m \in \mathbb {N}} \in \mathbb {Q}^{\mathbb {N}}$
.
-
1. If
 $(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to an irrational number
$(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to an irrational number
 $t \in \mathbb {R} \setminus \mathbb {Q}$
, then the sequence of right q-deformed rational numbers
$t \in \mathbb {R} \setminus \mathbb {Q}$
, then the sequence of right q-deformed rational numbers
 $([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to a limit uniquely determined by t.
$([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to a limit uniquely determined by t. -
2. If
 $(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to a rational number
$(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to a rational number
 $r/s$
from the right, then the sequence of right q-deformed rational numbers
$r/s$
from the right, then the sequence of right q-deformed rational numbers
 $([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to
$([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to
 $[r/s]_{q}^{\sharp }$
.
$[r/s]_{q}^{\sharp }$
. -
3. If
 $(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to a rational number
$(r_{m}/s_{m})_{m \in \mathbb {N}}$
converges to a rational number
 $r/s$
from the left, then the sequence of right q-deformed rational numbers
$r/s$
from the left, then the sequence of right q-deformed rational numbers
 $([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to
$([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}} \in \mathbb {R}^{\mathbb {N}}$
converges to
 $[r/s]_{q}^{\flat }$
.
$[r/s]_{q}^{\flat }$
.
By Theorem 2.12 Part (1), for every irrational number t, there is a unique q-deformation
![]() $[t]_{q}$
, which is the limit of the q-deformation of any rational sequence limiting to t. We call the set
$[t]_{q}$
, which is the limit of the q-deformation of any rational sequence limiting to t. We call the set
the q-deformed irrational numbers. See [Reference Leclere and Morier-Genoud12, Proposition 4.3, Examples 4.4–7] for an explicit formula for the q-deformation of quadratic irrational numbers.
Proof. First, we prove (1).
As noted in [Reference Leclere, Morier-Genoud, Ovsienko and Veselov13, Section 2], the negative q-rationals are the image of the positive q-rationals under the continuous bijection
with
![]() $\infty $
sent to
$\infty $
sent to
![]() $0$
and vice versa. Thus, it is sufficient to give a proof for positive t.
$0$
and vice versa. Thus, it is sufficient to give a proof for positive t.
Let
![]() $(r_{n}/s_{n})_{n \in \mathbb {N}}$
converge to a positive irrational number
$(r_{n}/s_{n})_{n \in \mathbb {N}}$
converge to a positive irrational number
![]() $t \in \mathbb {R} \setminus \mathbb {Q}$
. It is well-known that every irrational number has a unique infinite continued fraction expansion
$t \in \mathbb {R} \setminus \mathbb {Q}$
. It is well-known that every irrational number has a unique infinite continued fraction expansion
![]() $[a_{1},a_{2}, \ldots ]$
. We can approximate the sequence
$[a_{1},a_{2}, \ldots ]$
. We can approximate the sequence
![]() $(r_{n}/s_{n})_{n \in \mathbb {N}}$
by the ‘sequence of convergents’
$(r_{n}/s_{n})_{n \in \mathbb {N}}$
by the ‘sequence of convergents’
![]() $([a_{1},a_{2}, \ldots ,a_{n}])_{n \in \mathbb {N}}$
. Since
$([a_{1},a_{2}, \ldots ,a_{n}])_{n \in \mathbb {N}}$
. Since
![]() $[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
$[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
![]() $r/s>r'/s'$
, the right q-deformed sequence
$r/s>r'/s'$
, the right q-deformed sequence
![]() $([r_{n}/s_{n}]_{q}^{\sharp })_{n \in \mathbb {N}}$
is also approximated by
$([r_{n}/s_{n}]_{q}^{\sharp })_{n \in \mathbb {N}}$
is also approximated by
![]() $([a_{1},a_{2},\ldots ,a_{n}]_{q}^{\sharp })_{n \in \mathbb {N}}$
. Thus, we can assume without loss of generality that
$([a_{1},a_{2},\ldots ,a_{n}]_{q}^{\sharp })_{n \in \mathbb {N}}$
. Thus, we can assume without loss of generality that
![]() $r_{n}/s_{n}=[a_{1},a_{2},\ldots ,a_{n}]$
for all
$r_{n}/s_{n}=[a_{1},a_{2},\ldots ,a_{n}]$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
We split
![]() $(r_{n}/s_{n})_{n \in \mathbb {N}}$
into two disjoint subsequences. Define the index set
$(r_{n}/s_{n})_{n \in \mathbb {N}}$
into two disjoint subsequences. Define the index set
![]() $I\subset \mathbb {N}$
by
$I\subset \mathbb {N}$
by
Both
![]() $\lim_{n\in I} [r_n/s_n]_q^{\sharp}$
and
$\lim_{n\in I} [r_n/s_n]_q^{\sharp}$
and
![]() $\lim_{n \notin I} [r_n/s_n]_q^{\sharp}$
exist, as each sequence is monotone and bounded. Denote the former by
$\lim_{n \notin I} [r_n/s_n]_q^{\sharp}$
exist, as each sequence is monotone and bounded. Denote the former by
![]() $[t]_{q}^{-}$
and the latter by
$[t]_{q}^{-}$
and the latter by
![]() $[t]_{q}^{+}$
.
$[t]_{q}^{+}$
.
We would like to show
![]() $[t]_{q}^{-}=[t]_{q}^{+}$
. It is sufficient to show that
$[t]_{q}^{-}=[t]_{q}^{+}$
. It is sufficient to show that
Let
![]() $[r_{n}/s_{n}]_{q}^{\sharp }=\mathcal {R}^{\sharp }_{n}(q)/\mathcal {S}^{\sharp }_{n}(q)$
, and let
$[r_{n}/s_{n}]_{q}^{\sharp }=\mathcal {R}^{\sharp }_{n}(q)/\mathcal {S}^{\sharp }_{n}(q)$
, and let
![]() $[r_{n-1}/s_{n-1}]_{q}^{\sharp }=\mathcal {R}^{\sharp }_{n-1}(q)/\mathcal {S}^{\sharp }_{n-1}(q)$
, using the notation of Definition 2.7. By the matrix formula for right q-deformed rationals (Proposition 2.11), we have
$[r_{n-1}/s_{n-1}]_{q}^{\sharp }=\mathcal {R}^{\sharp }_{n-1}(q)/\mathcal {S}^{\sharp }_{n-1}(q)$
, using the notation of Definition 2.7. By the matrix formula for right q-deformed rationals (Proposition 2.11), we have
 $$ \begin{align*}\Big{\vert}\frac{\mathcal{R}^{\sharp}_{n}(q)}{\mathcal{S}^{\sharp}_{n}(q)}-\frac{\mathcal{R}^{\sharp}_{n-1}(q)}{\mathcal{S}^{\sharp}_{n-1}(q)}\Big{\vert}=q^{a_{2}+a_{4}+\cdots+a_{n}-1}\frac{{\vert}\det {\beta}_{\mathbf{a},q}{\vert}}{\mathcal{S}^{\sharp}_{n}(q)\mathcal{S}^{\sharp}_{n-1}(q)}.\end{align*} $$
$$ \begin{align*}\Big{\vert}\frac{\mathcal{R}^{\sharp}_{n}(q)}{\mathcal{S}^{\sharp}_{n}(q)}-\frac{\mathcal{R}^{\sharp}_{n-1}(q)}{\mathcal{S}^{\sharp}_{n-1}(q)}\Big{\vert}=q^{a_{2}+a_{4}+\cdots+a_{n}-1}\frac{{\vert}\det {\beta}_{\mathbf{a},q}{\vert}}{\mathcal{S}^{\sharp}_{n}(q)\mathcal{S}^{\sharp}_{n-1}(q)}.\end{align*} $$
By construction,
![]() $\mathcal {S}^{\sharp }_{n}(q)$
and
$\mathcal {S}^{\sharp }_{n}(q)$
and
![]() $\mathcal {S}^{\sharp }_{n-1}(q)$
both have constant term
$\mathcal {S}^{\sharp }_{n-1}(q)$
both have constant term
![]() $1$
and positive coefficients, so
$1$
and positive coefficients, so
![]() $\mathcal {S}^{\sharp }_{n}(q),\mathcal {S}^{\sharp }_{n-1}(q) \geq 1$
. And one can compute that
$\mathcal {S}^{\sharp }_{n}(q),\mathcal {S}^{\sharp }_{n-1}(q) \geq 1$
. And one can compute that
Therefore,
 $$ \begin{align*}\Big{\vert}\frac{\mathcal{R}^{\sharp}_{n}(q)}{\mathcal{S}^{\sharp}_{n}(q)}-\frac{\mathcal{R}^{\sharp}_{n-1}(q)}{\mathcal{S}^{\sharp}_{n-1}(q)}\Big{\vert}\leq q^{a_{1}+a_{3}+\cdots+a_{n-1}-1}.\end{align*} $$
$$ \begin{align*}\Big{\vert}\frac{\mathcal{R}^{\sharp}_{n}(q)}{\mathcal{S}^{\sharp}_{n}(q)}-\frac{\mathcal{R}^{\sharp}_{n-1}(q)}{\mathcal{S}^{\sharp}_{n-1}(q)}\Big{\vert}\leq q^{a_{1}+a_{3}+\cdots+a_{n-1}-1}.\end{align*} $$
(Technically, this assumes n is even; however, an all but identical argument works for n odd.) Given the assumption that t (and therefore also
![]() $\frac {r_{n}}{s_{n}}$
for sufficiently large n) are positive, we have
$\frac {r_{n}}{s_{n}}$
for sufficiently large n) are positive, we have
![]() $a_{1},\ldots ,a_{n-1}\geq 0$
. Since
$a_{1},\ldots ,a_{n-1}\geq 0$
. Since
![]() $q<1$
, we deduce that
$q<1$
, we deduce that
To prove that the limit is uniquely determined by t, we note again that
![]() $[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
$[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
![]() $r/s>r'/s'$
. Thus, between any two q-irrationals
$r/s>r'/s'$
. Thus, between any two q-irrationals
![]() $[t]_{q}, [t']_{q}$
for
$[t]_{q}, [t']_{q}$
for
![]() $t \neq t'$
, there is a right q-rational
$t \neq t'$
, there is a right q-rational
![]() $[r/s]_{q}^{\sharp }$
, so we cannot have
$[r/s]_{q}^{\sharp }$
, so we cannot have
![]() $[t]_{q}=[t']_{q}$
.
$[t]_{q}=[t']_{q}$
.
Now we prove (2). As in the irrational case, we can assume that
![]() $r/s$
is positive. Let
$r/s$
is positive. Let
![]() $[a_{1},\ldots ,a_{2n}]$
be the continued fraction expansion of
$[a_{1},\ldots ,a_{2n}]$
be the continued fraction expansion of
![]() $r/s$
. Any right limiting sequence approaching
$r/s$
. Any right limiting sequence approaching
![]() $r/s$
can be approximated by the sequence
$r/s$
can be approximated by the sequence
![]() $(r_{m}/s_{m})_{m \in \mathbb {N}}$
, where
$(r_{m}/s_{m})_{m \in \mathbb {N}}$
, where
![]() $r_{m}/s_{m}$
has continued fraction expansion
$r_{m}/s_{m}$
has continued fraction expansion
![]() $\mathbf {a}_{m}=[a_{1},\ldots ,a_{2n}-1,1,m]$
(unless
$\mathbf {a}_{m}=[a_{1},\ldots ,a_{2n}-1,1,m]$
(unless
![]() $a_{2n}=1$
, in which case
$a_{2n}=1$
, in which case
![]() $r_{m}/s_{m}$
has expansion
$r_{m}/s_{m}$
has expansion
![]() $\mathbf {a}_{m}=[a_{1},\ldots ,a_{2n-1}+1,m]$
). Since
$\mathbf {a}_{m}=[a_{1},\ldots ,a_{2n-1}+1,m]$
). Since
![]() $[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
$[r/s]_{q}^{\sharp }>[r'/s']_{q}^{\sharp }$
if and only if
![]() $r/s>r'/s'$
, the corresponding right q-deformed sequence is also approximated by
$r/s>r'/s'$
, the corresponding right q-deformed sequence is also approximated by
![]() $([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}}$
.
$([r_{m}/s_{m}]_{q}^{\sharp })_{m \in \mathbb {N}}$
.
Let
![]() $[{r}/{s}]_{q}^{\sharp }=\mathcal {R}^{\sharp }(q)/\mathcal {S}^{\sharp }(q)$
, and
$[{r}/{s}]_{q}^{\sharp }=\mathcal {R}^{\sharp }(q)/\mathcal {S}^{\sharp }(q)$
, and
![]() $[r_{m}/s_{m}]_{q}^{\sharp }=\mathcal {R}_{m}^{\sharp }(q)/\mathcal {S}_{m}^{\sharp }(q)$
, as defined in Definition 2.7. We view the right q-deformed rational numbers as vectors in projective space. Applying the matrix formula for right q-rationals (Proposition 2.11), we have
$[r_{m}/s_{m}]_{q}^{\sharp }=\mathcal {R}_{m}^{\sharp }(q)/\mathcal {S}_{m}^{\sharp }(q)$
, as defined in Definition 2.7. We view the right q-deformed rational numbers as vectors in projective space. Applying the matrix formula for right q-rationals (Proposition 2.11), we have
 $$ \begin{align*} \lim_{m \to \infty}\begin{bmatrix} \frac{q^{1-m}}{[m]_{q^{-1}}}\mathcal{R}_{m}^{\sharp}(q) \\ \frac{q^{1-m}}{[m]_{q^{-1}}}\mathcal{S}_{m}^{\sharp}(q) \end{bmatrix}&=\lim_{m \to \infty}\frac{1}{[m]_{q^{-1}}}q^{a_{2}+a_{4}+\cdots+a_{2n}}{\beta}_{\mathbf{a}_{m},q}\begin{bmatrix}1 \\ 0\end{bmatrix} \\&=q^{a_{2}+a_{4}+\cdots+a_{2n}}\sigma_{1,q}^{-a_{1}}\sigma_{2,q}^{a_{2}}\dots\sigma_{1,q}^{-a_{2n-1}}\sigma_{2,q}^{a_{2n}-1}\sigma_{1,q}^{-1}\begin{bmatrix} 0 & 0\\ 1 & q^{-1} -1\end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ &=\begin{bmatrix}\mathcal{R}^{\sharp}(q)\\ \mathcal{S}^{\sharp}(q)\end{bmatrix}. \end{align*} $$
$$ \begin{align*} \lim_{m \to \infty}\begin{bmatrix} \frac{q^{1-m}}{[m]_{q^{-1}}}\mathcal{R}_{m}^{\sharp}(q) \\ \frac{q^{1-m}}{[m]_{q^{-1}}}\mathcal{S}_{m}^{\sharp}(q) \end{bmatrix}&=\lim_{m \to \infty}\frac{1}{[m]_{q^{-1}}}q^{a_{2}+a_{4}+\cdots+a_{2n}}{\beta}_{\mathbf{a}_{m},q}\begin{bmatrix}1 \\ 0\end{bmatrix} \\&=q^{a_{2}+a_{4}+\cdots+a_{2n}}\sigma_{1,q}^{-a_{1}}\sigma_{2,q}^{a_{2}}\dots\sigma_{1,q}^{-a_{2n-1}}\sigma_{2,q}^{a_{2n}-1}\sigma_{1,q}^{-1}\begin{bmatrix} 0 & 0\\ 1 & q^{-1} -1\end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ &=\begin{bmatrix}\mathcal{R}^{\sharp}(q)\\ \mathcal{S}^{\sharp}(q)\end{bmatrix}. \end{align*} $$
The final claim (3) can be proved in essentially the same way as (2), replacing the sequence
![]() $[a_{1},\ldots ,a_{2n}-1,1,m]$
with the sequence
$[a_{1},\ldots ,a_{2n}-1,1,m]$
with the sequence
![]() $[a_{1},\ldots ,a_{2n},m]$
.
$[a_{1},\ldots ,a_{2n},m]$
.
Remark 2.13. In the preceding proof, we found that right q-deformed rationals correspond to limits of sequences of the form
![]() $([a_{1},\ldots ,a_{2n+1},m]_{q}^{\sharp })_{m \in \mathbb {Z}}$
, and left q-deformed rationals correspond to limits of sequences of the form
$([a_{1},\ldots ,a_{2n+1},m]_{q}^{\sharp })_{m \in \mathbb {Z}}$
, and left q-deformed rationals correspond to limits of sequences of the form
![]() $([a_{1},\ldots ,a_{2n},m]_{q}^{\sharp })_{m \in \mathbb {Z}}$
. Note that, for ordinary continued fractions,
$([a_{1},\ldots ,a_{2n},m]_{q}^{\sharp })_{m \in \mathbb {Z}}$
. Note that, for ordinary continued fractions,
Thus, in a sense, right q-rationals correspond to odd continued fraction expansions, and left q-rationals to even continued fraction expansions.
2.5 Topology of the q-Farey tessellation
We briefly summarise here the most important topological feature of the q-deformed Farey tessellation: it is an open disk, and the boundary of its closure is a circle, consisting of exactly the q-deformed rational curves and the q-deformed irrational numbers. Recall that
![]() $\mathbb {Q}_{q}$
denotes the union of the q-deformed rational curves (including their endpoints, the left and right q-deformed rational numbers), and that
$\mathbb {Q}_{q}$
denotes the union of the q-deformed rational curves (including their endpoints, the left and right q-deformed rational numbers), and that
![]() $\mathbb {I}_{q}$
denotes the q-deformed irrational numbers.
$\mathbb {I}_{q}$
denotes the q-deformed irrational numbers.
Proposition 2.14. Let
![]() $L_{q}$
denote the proper subset of
$L_{q}$
denote the proper subset of
![]() $\mathbb {H}$
covered by the q-deformed Farey tessellation.
$\mathbb {H}$
covered by the q-deformed Farey tessellation.
-
1. The set
 $L_{q}$
is homeomorphic to an open disk.
$L_{q}$
is homeomorphic to an open disk. -
2. The boundary
 $\partial \overline {L}_{q}$
is equal to
$\partial \overline {L}_{q}$
is equal to
 $\mathbb {Q}_{q} \sqcup \mathbb {I}_{q}$
.
$\mathbb {Q}_{q} \sqcup \mathbb {I}_{q}$
. -
3. There is a homeomorphism
 $\mathbb {Q}_{q} \sqcup \mathbb {I}_{q} \to \mathbb {R} \cup \{\infty \}$
, which restricts to the identity on the left and right q-deformed rationals and the q-deformed irrationals. So, by Part (2),
$\mathbb {Q}_{q} \sqcup \mathbb {I}_{q} \to \mathbb {R} \cup \{\infty \}$
, which restricts to the identity on the left and right q-deformed rationals and the q-deformed irrationals. So, by Part (2),
 $\partial \overline {L}_{q} \cong \mathbb {R}\cup \{\infty \}$
.
$\partial \overline {L}_{q} \cong \mathbb {R}\cup \{\infty \}$
. -
4. The set
 $\mathbb {Q}_{q}$
is dense in
$\mathbb {Q}_{q}$
is dense in
 $\partial \overline {L}_{q}$
.
$\partial \overline {L}_{q}$
.
We expect the following conjecture to hold as well.
Conjecture 2.15. The closure of the q-deformed Farey tessellation
![]() $\overline {L}_{q}$
is homeomorphic to a closed disk.
$\overline {L}_{q}$
is homeomorphic to a closed disk.
Because the q-deformed rational curves are dense in the boundary of
![]() $\overline {L}_{q}$
, these curves are arguably the true q-deformed analogues of the rational numbers, hence the notation
$\overline {L}_{q}$
, these curves are arguably the true q-deformed analogues of the rational numbers, hence the notation
![]() $\mathbb {Q}_q$
for their union.
$\mathbb {Q}_q$
for their union.
Proof of Proposition 2.14.
Part (1) of Proposition 2.14 is true by construction; the q-deformed Farey tessellation is homeomorphic to the classical Farey tessellation, which is homeomorphic to an open disk.
The homological counterpart of Part (2) is Theorem 5.15 below, and the proof of Part (2) is virtually the same as the proof of Theorem 5.15.
We will prove Part (3). Part (4) follows immediately from Part (3) and Theorem 2.12.
It is not hard to check that for any two real numbers
![]() $t<t'$
(which may be rational or irrational), we have the following inequalities:
$t<t'$
(which may be rational or irrational), we have the following inequalities:
The left (resp. right) weak inequality is strict if and only if t (resp.
![]() $t'$
) is rational. Define an embedding
$t'$
) is rational. Define an embedding
![]() $\iota :\mathbb {Q}_{q} \sqcup \mathbb {I}_{q} \to \mathbb {R} \cup \{\infty \}$
as follows. For
$\iota :\mathbb {Q}_{q} \sqcup \mathbb {I}_{q} \to \mathbb {R} \cup \{\infty \}$
as follows. For
![]() $t \in \mathbb {R} \cup \{\infty \}$
,
$t \in \mathbb {R} \cup \{\infty \}$
,
Extend
![]() $\iota $
to
$\iota $
to
![]() $\mathbb {Q}_{q}$
by continuously mapping the hyperbolic geodesic between
$\mathbb {Q}_{q}$
by continuously mapping the hyperbolic geodesic between
![]() $[r/s]_{q}^{\flat }$
and
$[r/s]_{q}^{\flat }$
and
![]() $[r/s]_{q}^{\sharp }$
onto the real interval between
$[r/s]_{q}^{\sharp }$
onto the real interval between
![]() $[r/s]_{q}^{\flat }$
and
$[r/s]_{q}^{\flat }$
and
![]() $[r/s]_{q}^{\sharp }$
. By Eq. (2.2),
$[r/s]_{q}^{\sharp }$
. By Eq. (2.2),
![]() $\iota $
is indeed an embedding.
$\iota $
is indeed an embedding.
To complete the proof, we just need to show that
![]() $\iota $
is surjective. Consider any
$\iota $
is surjective. Consider any
![]() $p \in \mathbb {R} \cup \{\infty \}$
. For convenience, assume that
$p \in \mathbb {R} \cup \{\infty \}$
. For convenience, assume that
![]() $0 < p <\infty $
. Suppose that
$0 < p <\infty $
. Suppose that
![]() $p \notin \iota (\mathbb {Q}_{q})$
; we will show that
$p \notin \iota (\mathbb {Q}_{q})$
; we will show that
![]() $p \in \mathbb {I}_{q}$
. By assumption, p does not lie in the interval in
$p \in \mathbb {I}_{q}$
. By assumption, p does not lie in the interval in
![]() $\mathbb {R} \cup \{\infty \}$
between
$\mathbb {R} \cup \{\infty \}$
between
![]() $[\infty ]_q^{\flat }$
and
$[\infty ]_q^{\flat }$
and
![]() $[\infty ]_q^{\sharp }$
. By the proof of Theorem 2.12, the sequence
$[\infty ]_q^{\sharp }$
. By the proof of Theorem 2.12, the sequence
![]() $[n]^{\sharp }_{q}$
for
$[n]^{\sharp }_{q}$
for
![]() $n \geq 0$
is a monotone increasing sequence converging to
$n \geq 0$
is a monotone increasing sequence converging to
![]() $[\infty ]_{q}^{\flat }$
. So, there exists
$[\infty ]_{q}^{\flat }$
. So, there exists
![]() $a_{1} \geq 0$
such that
$a_{1} \geq 0$
such that
The sequence
![]() $[a_{1},n]_{q}^{\sharp }$
for
$[a_{1},n]_{q}^{\sharp }$
for
![]() $n\geq 1$
is a monotone decreasing sequence converging to
$n\geq 1$
is a monotone decreasing sequence converging to
![]() $[a_{1}]_{q}^{\sharp }$
by the proof of Theorem 2.12. Since
$[a_{1}]_{q}^{\sharp }$
by the proof of Theorem 2.12. Since
![]() $p>[a_{1}]_{q}^{\sharp }$
, there exists
$p>[a_{1}]_{q}^{\sharp }$
, there exists
![]() $a_{2} \geq 1$
such that
$a_{2} \geq 1$
such that
Continuing in this manner, we obtain an infinite q-deformed continued fraction expansion
![]() $[a_{1},a_{2},\ldots ]_{q}^{\sharp }$
converging to p. By the first part of Theorem 2.12, the number p is the q-deformation of the irrational number with continued fraction expansion
$[a_{1},a_{2},\ldots ]_{q}^{\sharp }$
converging to p. By the first part of Theorem 2.12, the number p is the q-deformation of the irrational number with continued fraction expansion
![]() $[a_{1},a_{2},\ldots ]$
, which proves that
$[a_{1},a_{2},\ldots ]$
, which proves that
![]() $p \in \mathbb {I}_{q}$
as desired. This completes the proof.
$p \in \mathbb {I}_{q}$
as desired. This completes the proof.
3 Bridgeland stability conditions and Harder–Narasimhan automata
The remainder of the paper is concerned with the space of stability conditions on the
![]() $A_{2}$
2-Calabi–Yau category
$A_{2}$
2-Calabi–Yau category
![]() $\mathcal {C}_{2}$
. In particular, we show that the q-deformed rational numbers of Section 2 correspond to functionals on
$\mathcal {C}_{2}$
. In particular, we show that the q-deformed rational numbers of Section 2 correspond to functionals on
![]() $\mathcal {C}_{2}$
and appear, in this guise, as boundary points in a compactification of the space of stability conditions. Our main tool in proving the correspondence between q-rationals and functions on
$\mathcal {C}_{2}$
and appear, in this guise, as boundary points in a compactification of the space of stability conditions. Our main tool in proving the correspondence between q-rationals and functions on
![]() $\mathcal {C}_{2}$
will be an abstract gadget called a Harder–Narasimhan automaton, whose construction depends on the choice of a Bridgeland stability condition. In this section, we summarise relevant material from the theory of stability conditions and define the Harder–Narasimhan automaton.
$\mathcal {C}_{2}$
will be an abstract gadget called a Harder–Narasimhan automaton, whose construction depends on the choice of a Bridgeland stability condition. In this section, we summarise relevant material from the theory of stability conditions and define the Harder–Narasimhan automaton.
3.1 Background on Bridgeland stability conditions
We assume the reader is familiar with the theory of Bridgeland stability conditions [Reference Bridgeland4]. To briefly recall, a stability condition on a triangulated category is specified as
![]() $\tau = (\mathcal {P}_{\tau }, Z_{\tau })$
, where
$\tau = (\mathcal {P}_{\tau }, Z_{\tau })$
, where
![]() $\mathcal {P}_{\tau }$
is a slicing and
$\mathcal {P}_{\tau }$
is a slicing and
![]() $Z_{\tau }$
is a compatible central charge. An object of the category is called
$Z_{\tau }$
is a compatible central charge. An object of the category is called
![]() $\tau $
-semistable if it belongs to one of the full (abelian) subcategories
$\tau $
-semistable if it belongs to one of the full (abelian) subcategories
![]() $\mathcal {P}_{\tau }(\phi )$
for some
$\mathcal {P}_{\tau }(\phi )$
for some
![]() $\phi \in \mathbb {R}$
. In this case, the number
$\phi \in \mathbb {R}$
. In this case, the number
![]() $\phi $
is called the phase of that semistable object. An object is called
$\phi $
is called the phase of that semistable object. An object is called
![]() $\tau $
-stable if it is semistable (of some phase
$\tau $
-stable if it is semistable (of some phase
![]() $\phi $
) and, moreover, if it is simple in the abelian category
$\phi $
) and, moreover, if it is simple in the abelian category
![]() $\mathcal {P}_{\tau }(\phi )$
.
$\mathcal {P}_{\tau }(\phi )$
.
Recall also that every object of the category has a unique Harder–Narasimhan filtration with respect to
![]() $\tau $
.
$\tau $
.
Definition 3.1. Fix a stability condition
![]() $\tau $
on a triangulated category. Let X be any object of the category. The
$\tau $
on a triangulated category. Let X be any object of the category. The
![]() $\tau $
-Harder–Narasimhan filtration of X is the unique filtration
$\tau $
-Harder–Narasimhan filtration of X is the unique filtration

with the following properties.
-
1. Each filtration factor
 $A_i$
is semistable of some phase
$A_i$
is semistable of some phase
 $\phi _i$
, and
$\phi _i$
, and -
2. The numbers
 $\phi _i$
appear in decreasing order:
$\phi _i$
appear in decreasing order:
 $\phi _1> \phi _2 \cdots > \phi _n$
.
$\phi _1> \phi _2 \cdots > \phi _n$
.
Let
![]() $\mathcal {T}$
denote an arbitrary triangulated category. Recall that for any subset
$\mathcal {T}$
denote an arbitrary triangulated category. Recall that for any subset
![]() $I \subset \mathbb {R}$
, we define
$I \subset \mathbb {R}$
, we define
![]() $\mathcal {P}_{\tau }(I)$
to be the full subcategory of
$\mathcal {P}_{\tau }(I)$
to be the full subcategory of
![]() $\mathcal {T}$
consisting of objects whose Harder–Narasimhan filtration factors have phases in I. The subcategory
$\mathcal {T}$
consisting of objects whose Harder–Narasimhan filtration factors have phases in I. The subcategory
![]() $\mathcal {P}_{\tau }([0,1))$
corresponding to the half-open interval
$\mathcal {P}_{\tau }([0,1))$
corresponding to the half-open interval
![]() $[0,1) \subset \mathbb {R}$
is a full abelian subcategory of
$[0,1) \subset \mathbb {R}$
is a full abelian subcategory of
![]() $\mathcal T$
, which is the heart of a bounded t-structure on
$\mathcal T$
, which is the heart of a bounded t-structure on
![]() $\mathcal T$
(see [Reference Bridgeland4, Section 3]).
$\mathcal T$
(see [Reference Bridgeland4, Section 3]).
Let
![]() $\Sigma _{\tau }$
denote the set of indecomposable semistable objects of
$\Sigma _{\tau }$
denote the set of indecomposable semistable objects of
![]() $\mathcal T$
that lie in
$\mathcal T$
that lie in
![]() $\mathcal {P}_{\tau }([0,1))$
. Then every indecomposable semistable object lies in
$\mathcal {P}_{\tau }([0,1))$
. Then every indecomposable semistable object lies in
![]() $\Sigma _{\tau }$
up to an integer shift. We can count the (graded) multiplicity of any object of
$\Sigma _{\tau }$
up to an integer shift. We can count the (graded) multiplicity of any object of
![]() $\mathcal T$
in a given object of
$\mathcal T$
in a given object of
![]() $\Sigma _{\tau }$
, as follows.
$\Sigma _{\tau }$
, as follows.
Definition 3.2. Fix some
![]() $q> 0$
. The
$q> 0$
. The
![]() $\tau $
-Harder–Narasimhan multiplicity vector (or simply the HN multiplicity vector) of a semistable object
$\tau $
-Harder–Narasimhan multiplicity vector (or simply the HN multiplicity vector) of a semistable object
![]() $A \in \mathcal T$
is an element of
$A \in \mathcal T$
is an element of
![]() $\mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
, defined as follows. Let k be such that
$\mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
, defined as follows. Let k be such that
![]() $A \in \mathcal {P}_{\tau }([k,k+1))$
. For any
$A \in \mathcal {P}_{\tau }([k,k+1))$
. For any
![]() $B \in \Sigma _{\tau }$
, let
$B \in \Sigma _{\tau }$
, let
![]() $n_{B}$
be the number of indecomposable summands of A that are isomorphic to B. Then the coordinate of the HN multiplicity vector of A at
$n_{B}$
be the number of indecomposable summands of A that are isomorphic to B. Then the coordinate of the HN multiplicity vector of A at
![]() $B \in \Sigma _{\tau }$
is
$B \in \Sigma _{\tau }$
is
![]() $n_{B} q^{k}$
.
$n_{B} q^{k}$
.
The
![]() $\tau $
-Harder–Narasimhan multiplicity vector of a general object of
$\tau $
-Harder–Narasimhan multiplicity vector of a general object of
![]() $\mathcal T$
is defined as the sum of the
$\mathcal T$
is defined as the sum of the
![]() $\tau $
-Harder–Narasimhan multiplicity vectors of its
$\tau $
-Harder–Narasimhan multiplicity vectors of its
![]() $\tau $
-Harder–Narasimhan filtration factors.
$\tau $
-Harder–Narasimhan filtration factors.
Next, we introduce a graded version of Harder–Narasimhan mass (see [Reference Dimitrov, Haiden, Katzarkov and Kontsevich5, Section 4.5], [Reference Ikeda8, Section 3]).
Definition 3.3. Let
![]() $\tau $
be a stability condition on a triangulated category
$\tau $
be a stability condition on a triangulated category
![]() $\mathcal T$
. Let q be a fixed positive real number. Let X be an object of
$\mathcal T$
. Let q be a fixed positive real number. Let X be an object of
![]() $\mathcal T$
and consider its Harder–Narasimhan filtration:
$\mathcal T$
and consider its Harder–Narasimhan filtration:

Let
![]() $\phi _i$
denote the phase of the semistable object
$\phi _i$
denote the phase of the semistable object
![]() $A_i$
. The q-Harder–Narasimhan mass, or q-mass, of the object X is defined to be
$A_i$
. The q-Harder–Narasimhan mass, or q-mass, of the object X is defined to be
 $$\begin{align*}m_{q,\tau}(X) = \sum_{i = 1}^k q^{\phi_i}|Z_{\tau}(A_i)|.\end{align*}$$
$$\begin{align*}m_{q,\tau}(X) = \sum_{i = 1}^k q^{\phi_i}|Z_{\tau}(A_i)|.\end{align*}$$
Note that for
![]() $q = 1$
, the q-Harder–Narasimhan mass is simply the classical Harder–Narasimhan mass as defined in [Reference Bridgeland4, Section 5]. The q-mass function is due to [Reference Dimitrov, Haiden, Katzarkov and Kontsevich5, Section 4.4].
$q = 1$
, the q-Harder–Narasimhan mass is simply the classical Harder–Narasimhan mass as defined in [Reference Bridgeland4, Section 5]. The q-mass function is due to [Reference Dimitrov, Haiden, Katzarkov and Kontsevich5, Section 4.4].
Finally, we denote the space of stability conditions on a triangulated category
![]() $\mathcal T$
by
$\mathcal T$
by
![]() $\operatorname {\mathrm {Stab}}(\mathcal T)$
. There is a natural
$\operatorname {\mathrm {Stab}}(\mathcal T)$
. There is a natural
![]() $\mathbb {C}$
-action on
$\mathbb {C}$
-action on
![]() $\operatorname {\mathrm {Stab}}(\mathcal T)$
defined as follows.
$\operatorname {\mathrm {Stab}}(\mathcal T)$
defined as follows.
For
![]() $z = a + i\pi b \in \mathbb {C}$
and a stability condition
$z = a + i\pi b \in \mathbb {C}$
and a stability condition
![]() ${\tau }=(\mathcal {P}_{{\tau }},Z_{{\tau }})$
, define
${\tau }=(\mathcal {P}_{{\tau }},Z_{{\tau }})$
, define
![]() $z{\tau }=(\mathcal {P}_{z{\tau }}, Z_{z{\tau }})$
by
$z{\tau }=(\mathcal {P}_{z{\tau }}, Z_{z{\tau }})$
by
So for any
![]() $X \in \mathcal {T}$
, the action of
$X \in \mathcal {T}$
, the action of
![]() $z = a + i \pi b$
rotates the vector
$z = a + i \pi b$
rotates the vector
![]() $Z(X)$
by the angle
$Z(X)$
by the angle
![]() $\pi b$
, scales it by the quantity
$\pi b$
, scales it by the quantity
![]() $e^a$
, and simultaneously shifts the slicing by the quantity b. We will always consider the space
$e^a$
, and simultaneously shifts the slicing by the quantity b. We will always consider the space
![]() $\operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C}$
, which is the space of stability conditions up to this natural
$\operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C}$
, which is the space of stability conditions up to this natural
![]() $\mathbb {C}$
action.
$\mathbb {C}$
action.
3.2 Harder–Narasimhan and mass automata
Fix throughout this section a stability condition
![]() $\tau $
on
$\tau $
on
![]() $\mathcal T$
. Recall that
$\mathcal T$
. Recall that
![]() $\Sigma _{\tau }$
is the set of indecomposable
$\Sigma _{\tau }$
is the set of indecomposable
![]() $\tau $
-semistable objects of
$\tau $
-semistable objects of
![]() $\mathcal T$
that lie in
$\mathcal T$
that lie in
![]() $\mathcal {P}_{\tau }([0,1))$
. For any
$\mathcal {P}_{\tau }([0,1))$
. For any
![]() $X \in \operatorname {\mathrm {Ob}} \mathcal T$
, set
$X \in \operatorname {\mathrm {Ob}} \mathcal T$
, set
![]() $\operatorname {\mathrm {HN}}_{\tau }(X) \in \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
to be the
$\operatorname {\mathrm {HN}}_{\tau }(X) \in \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
to be the
![]() $\tau $
-HN multiplicity vector of X. Suppose also that a group G acts on
$\tau $
-HN multiplicity vector of X. Suppose also that a group G acts on
![]() $\mathcal T$
.
$\mathcal T$
.
In this section, we define Harder–Narasimhan automata on
![]() $\mathcal T$
. Our definition is just a graded version of the one from [Reference Bapat, Deopurkar and Licata2, Section 3], but we recall the key elements here. We begin with some notation.
$\mathcal T$
. Our definition is just a graded version of the one from [Reference Bapat, Deopurkar and Licata2, Section 3], but we recall the key elements here. We begin with some notation.
Let
![]() $\Theta $
be an arbitrary quiver. Let
$\Theta $
be an arbitrary quiver. Let
![]() $\Theta _0$
and
$\Theta _0$
and
![]() $\Theta _1$
denote the sets of vertices and edges of
$\Theta _1$
denote the sets of vertices and edges of
![]() $\Theta $
, respectively. Given
$\Theta $
, respectively. Given
![]() $\alpha \in \Theta _1$
, we say that
$\alpha \in \Theta _1$
, we say that
![]() $s(\alpha )\in \Theta _0$
is its source, and
$s(\alpha )\in \Theta _0$
is its source, and
![]() $t(\alpha ) \in \Theta _0$
is its target.
$t(\alpha ) \in \Theta _0$
is its target.
A G-labelling of
![]() $\Theta $
is a function
$\Theta $
is a function
![]() $\Theta _1 \to G$
. Then, every path (finite sequence of composable edges) in
$\Theta _1 \to G$
. Then, every path (finite sequence of composable edges) in
![]() $\Theta $
automatically acquires a label, namely the product of the corresponding group elements in reverse order.
$\Theta $
automatically acquires a label, namely the product of the corresponding group elements in reverse order.
A
![]() $\Theta $
-set
$\Theta $
-set
![]() $\underline {S}$
is a representation of
$\underline {S}$
is a representation of
![]() $\Theta $
in the category of sets. More precisely, it is specified by a collection of sets
$\Theta $
in the category of sets. More precisely, it is specified by a collection of sets
![]() $\{S_v \mid v \in \Theta _0\}$
, together with edge functions
$\{S_v \mid v \in \Theta _0\}$
, together with edge functions
![]() $\{f_{\alpha } \colon S_{s(\alpha )} \to S_{t(\alpha )} \mid \alpha \in \Theta _1\}$
.
$\{f_{\alpha } \colon S_{s(\alpha )} \to S_{t(\alpha )} \mid \alpha \in \Theta _1\}$
.
Let A be any ring. A
![]() $\Theta $
-representation
$\Theta $
-representation
![]() $\underline {M}$
of A-modules consists (as usual) of A-modules
$\underline {M}$
of A-modules consists (as usual) of A-modules
![]() $\{M_v \mid v \in \Theta _0\}$
and A-linear maps
$\{M_v \mid v \in \Theta _0\}$
and A-linear maps
![]() $\{f_{\alpha } \colon M_{s(\alpha )} \to M_{t(\alpha )}\mid \alpha \in \Theta _1\}$
. Any
$\{f_{\alpha } \colon M_{s(\alpha )} \to M_{t(\alpha )}\mid \alpha \in \Theta _1\}$
. Any
![]() $\Theta $
-representation is also a
$\Theta $
-representation is also a
![]() $\Theta $
-set.
$\Theta $
-set.
A morphism of
![]() $\Theta $
-sets (resp.
$\Theta $
-sets (resp.
![]() $\Theta $
-representations) consists of maps between the sets (resp. module maps between the modules) at each vertex, so that the square determined by every edge commutes.
$\Theta $
-representations) consists of maps between the sets (resp. module maps between the modules) at each vertex, so that the square determined by every edge commutes.
A G-set S, together with a G-labelling on
![]() $\ell \colon \Theta _1 \to G$
, naturally produces a
$\ell \colon \Theta _1 \to G$
, naturally produces a
![]() $\Theta $
-set, as follows. We declare each
$\Theta $
-set, as follows. We declare each
![]() $S_v$
to be S for every
$S_v$
to be S for every
![]() $v \in \Theta _0$
, and each
$v \in \Theta _0$
, and each
![]() $f_{\alpha } \colon S \to S$
to be the action of
$f_{\alpha } \colon S \to S$
to be the action of
![]() $\ell (\alpha )$
on S. In particular,
$\ell (\alpha )$
on S. In particular,
![]() $\operatorname {\mathrm {Ob}} \mathcal T$
is a
$\operatorname {\mathrm {Ob}} \mathcal T$
is a
![]() $\Theta $
-set, and we denote this as
$\Theta $
-set, and we denote this as
![]() $\underline {\operatorname {\mathrm {Ob}} \mathcal T}$
. Similarly, any G-representation, together with a G-labelling of
$\underline {\operatorname {\mathrm {Ob}} \mathcal T}$
. Similarly, any G-representation, together with a G-labelling of
![]() $\Theta $
, naturally produces a
$\Theta $
, naturally produces a
![]() $\Theta $
-representation.
$\Theta $
-representation.
Definition 3.4. Fix some
![]() $q> 0$
. A
$q> 0$
. A
![]() $\tau $
-HN automaton for the G-action on
$\tau $
-HN automaton for the G-action on
![]() $\mathcal T$
consists of the following data.
$\mathcal T$
consists of the following data.
-
1. A G-labelled quiver
 $\Theta $
(and hence the
$\Theta $
(and hence the
 $\Theta $
-set
$\Theta $
-set
 $\underline {\operatorname {\mathrm {Ob}} \mathcal T}$
).
$\underline {\operatorname {\mathrm {Ob}} \mathcal T}$
). -
2. A
 $\Theta $
-subset
$\Theta $
-subset
 $\underline {S} \subset \underline {\operatorname {\mathrm {Ob}} \mathcal T}$
.
$\underline {S} \subset \underline {\operatorname {\mathrm {Ob}} \mathcal T}$
. -
3. A
 $\Theta $
-representation
$\Theta $
-representation
 $\underline {M}$
of
$\underline {M}$
of
 $\mathbb {Z}[q^{\pm }]$
-modules.
$\mathbb {Z}[q^{\pm }]$
-modules. -
4. A morphism
 $i \colon \underline {S} \to \underline {M}$
.
$i \colon \underline {S} \to \underline {M}$
. -
5. A
 $\mathbb {Z}[q^{\pm }]$
-linear map
$\mathbb {Z}[q^{\pm }]$
-linear map
 $h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
for every
$h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
for every
 $v \in \Theta _0$
.
$v \in \Theta _0$
.
This data is required to satisfy
for every
![]() $v \in \Theta _0$
and every
$v \in \Theta _0$
and every
![]() $s \in S = S_v$
.
$s \in S = S_v$
.
Example 3.5. We illustrate the above definition with the following (somewhat trivial) example. Let
![]() $\mathcal T$
be any triangulated category and fix a stability condition
$\mathcal T$
be any triangulated category and fix a stability condition
![]() $\tau $
on it. Let G be the group
$\tau $
on it. Let G be the group
![]() $\mathbb {Z}$
, generated by the triangulated shift
$\mathbb {Z}$
, generated by the triangulated shift
![]() $(-)[1]$
. Then, an example of an HN automaton for this setup is given by the following data.
$(-)[1]$
. Then, an example of an HN automaton for this setup is given by the following data.
-
1. An infinite
 $\mathbb {Z}$
-labelled quiver
$\mathbb {Z}$
-labelled quiver
 $\Theta $
.
$\Theta $
. 
-
2. The following
 $\Theta $
-subset
$\Theta $
-subset
 $\underline {S} \subset \underline {\operatorname {\mathrm {Ob}} \mathcal T}$
.
$\underline {S} \subset \underline {\operatorname {\mathrm {Ob}} \mathcal T}$
. 
-
3. The following
 $\Theta $
-representation
$\Theta $
-representation
 $\underline {M}$
.
$\underline {M}$
. 
-
4. The morphism
 $i \colon \underline {S} \to \underline {M}$
is as follows. For any
$i \colon \underline {S} \to \underline {M}$
is as follows. For any
 $j \in \mathbb {Z}$
, the map
$j \in \mathbb {Z}$
, the map
 $i_j \colon S_j \to M_j$
is defined as
$i_j \colon S_j \to M_j$
is defined as  $$\begin{align*}i_j(X) = \operatorname{\mathrm{HN}}_{\tau}(X).\end{align*}$$
$$\begin{align*}i_j(X) = \operatorname{\mathrm{HN}}_{\tau}(X).\end{align*}$$
With this definition, i is
 $\Theta $
-equivariant (i.e., a morphism) because
$\Theta $
-equivariant (i.e., a morphism) because  $$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X[1]) = q\cdot \operatorname{\mathrm{HN}}_{\tau}(X).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X[1]) = q\cdot \operatorname{\mathrm{HN}}_{\tau}(X).\end{align*}$$
-
5. Finally, for each
 $j \in \mathbb {Z}$
, the map
$j \in \mathbb {Z}$
, the map
 $h_j \colon M_j \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
is just the identity map. The compatibility condition
$h_j \colon M_j \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
is just the identity map. The compatibility condition  $$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X) = h_j(i_j(X))\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X) = h_j(i_j(X))\end{align*}$$
is obvious.
Remark 3.6. The example above merely serves to illustrate the definition and does not compute anything interesting. However, appropriately engineered Harder–Narasimhan automata can be extremely useful for calculations, particularly for results about dynamics of autoequivalences in the category. An example of a computationally useful HN automaton is described in Section 4.1 of this paper. Other examples can be found in [Reference Bapat, Deopurkar and Licata2].
We also have the analogue of a mass automaton, as described in [Reference Bapat, Deopurkar and Licata2, Section 3].
Definition 3.7. Let q be a fixed positive real number. A
![]() $\tau $
-mass automaton is analogous to a
$\tau $
-mass automaton is analogous to a
![]() $\tau $
-HN automaton, with the definition modified as follows. The maps
$\tau $
-HN automaton, with the definition modified as follows. The maps
![]() $h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
are replaced by linear maps
$h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
are replaced by linear maps
![]() $m_v \colon M_v \to \mathbb {R}$
, satisfying
$m_v \colon M_v \to \mathbb {R}$
, satisfying
In particular, given an HN automaton for a stability condition
![]() $\tau $
and a fixed
$\tau $
and a fixed
![]() $q> 0$
, we can produce a
$q> 0$
, we can produce a
![]() $\tau $
-mass automaton by composing the HN vector with the q-mass function.
$\tau $
-mass automaton by composing the HN vector with the q-mass function.
4 A homological interpretation of q-deformed rational numbers
The aim of this section is to give a concrete homological interpretation of q-deformed rational numbers. We write down a particular Harder–Narasimhan automaton for the 2-Calabi–Yau category associated to the
![]() $A_2$
quiver, which yields the desired application.
$A_2$
quiver, which yields the desired application.
4.1 The 2-Calabi–Yau category associated to the
 $A_{2}$
quiver
$A_{2}$
quiver
We follow the construction of the 2-Calabi–Yau category associated to the
![]() $A_2$
quiver given in [Reference Seidel and Thomas18, Section 4.1] and [Reference Bapat, Deopurkar and Licata2, Section 2.1]. Let
$A_2$
quiver given in [Reference Seidel and Thomas18, Section 4.1] and [Reference Bapat, Deopurkar and Licata2, Section 2.1]. Let
![]() $P(A_2)$
denote the path algebra of the double of the
$P(A_2)$
denote the path algebra of the double of the
![]() $A_2$
quiver. This quiver has two vertices, denoted
$A_2$
quiver. This quiver has two vertices, denoted
![]() $1$
and
$1$
and
![]() $2$
, and two oriented edges, one from
$2$
, and two oriented edges, one from
![]() $1$
to
$1$
to
![]() $2$
and the other from
$2$
and the other from
![]() $2$
to
$2$
to
![]() $1$
. We denote by
$1$
. We denote by
![]() $Z_{2}$
the quotient of this path algebra by the two-sided ideal generated by all paths of length 3. We regard
$Z_{2}$
the quotient of this path algebra by the two-sided ideal generated by all paths of length 3. We regard
![]() $Z_2$
as a differential graded algebra with grading by path length, and zero differential. Let
$Z_2$
as a differential graded algebra with grading by path length, and zero differential. Let
![]() ${ \mathsf {DGM}}_{2}$
be the category of differential graded modules over
${ \mathsf {DGM}}_{2}$
be the category of differential graded modules over
![]() $Z_{2}$
, and let
$Z_{2}$
, and let
![]() $\mathcal {D}_{2}$
be the derived category of differential graded modules over
$\mathcal {D}_{2}$
be the derived category of differential graded modules over
![]() $Z_{2}$
(obtained from
$Z_{2}$
(obtained from
![]() ${ \mathsf {DGM}}_{2}$
by inverting quasi-isomorphisms; note that this is not the same as the standard derived category of the abelian category
${ \mathsf {DGM}}_{2}$
by inverting quasi-isomorphisms; note that this is not the same as the standard derived category of the abelian category
![]() ${ \mathsf {DGM}}_{2}$
). For
${ \mathsf {DGM}}_{2}$
). For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $P_{i}$
denote the differential graded module
$P_{i}$
denote the differential graded module
![]() $Z_{2}(i)$
, where
$Z_{2}(i)$
, where
![]() $(i)$
is the trivial path at the vertex i. The objects
$(i)$
is the trivial path at the vertex i. The objects
![]() $\{P_{1},P_{2}\}$
form an
$\{P_{1},P_{2}\}$
form an
![]() $A_{2}$
configuration of spherical objects in
$A_{2}$
configuration of spherical objects in
![]() $\mathcal {D}_{2}$
, in the sense of [Reference Seidel and Thomas18, Definition 1.1]. Let
$\mathcal {D}_{2}$
, in the sense of [Reference Seidel and Thomas18, Definition 1.1]. Let
![]() $\mathcal {C}_{2}$
denote the full triangulated subcategory of
$\mathcal {C}_{2}$
denote the full triangulated subcategory of
![]() $\mathcal {D}_{2}$
generated by
$\mathcal {D}_{2}$
generated by
![]() $P_{1},P_{2}$
under extensions. Then,
$P_{1},P_{2}$
under extensions. Then,
![]() $\mathcal {C}_{2}$
is a 2-Calabi–Yau category.
$\mathcal {C}_{2}$
is a 2-Calabi–Yau category.
Especially important for our purposes are the following structural features of
![]() $\mathcal {C}_{2}$
.
$\mathcal {C}_{2}$
.
-
1. There is a unique morphism (up to scaling) from
 $P_1$
to
$P_1$
to
 $P_2$
, and also from
$P_2$
, and also from
 $P_2$
to
$P_2$
to
 $P_1$
. We denote the cones of these morphisms by
$P_1$
. We denote the cones of these morphisms by
 $P_{12}$
and
$P_{12}$
and
 $P_{21}$
, respectively. They are indecomposable spherical objects of
$P_{21}$
, respectively. They are indecomposable spherical objects of
 $\mathcal {C}_{2}$
.
$\mathcal {C}_{2}$
. -
2. The extension closure of
 $P_{1},P_{2}$
is the heart of a bounded t-structure on
$P_{1},P_{2}$
is the heart of a bounded t-structure on
 $\mathcal {C}_{2}$
. We call this t-structure the standard t-structure on
$\mathcal {C}_{2}$
. We call this t-structure the standard t-structure on
 $\mathcal {C}_{2}$
and denote its heart by
$\mathcal {C}_{2}$
and denote its heart by
 $\heartsuit _{\operatorname {\mathrm {std}}}$
. Objects in the standard heart are direct sums of the indecomposables
$\heartsuit _{\operatorname {\mathrm {std}}}$
. Objects in the standard heart are direct sums of the indecomposables
 $P_{1}$
,
$P_{1}$
,
 $P_{2}$
,
$P_{2}$
,
 $P_{12}$
and
$P_{12}$
and
 $P_{21}$
.
$P_{21}$
. -
3. Every spherical object X in
 $\mathcal {C}_{2}$
gives rise to an autoequivalence
$\mathcal {C}_{2}$
gives rise to an autoequivalence
 $\sigma _{X}$
on
$\sigma _{X}$
on
 $\mathcal {C}_{2}$
known as the spherical twist along X. These autoequivalences form a group, generated by
$\mathcal {C}_{2}$
known as the spherical twist along X. These autoequivalences form a group, generated by
 $\sigma _{P_{1}},\sigma _{P_{2}}$
(henceforth simply
$\sigma _{P_{1}},\sigma _{P_{2}}$
(henceforth simply
 $\sigma _{1},\sigma _{2}$
). The group of spherical twists is isomorphic to the 3-strand braid group
$\sigma _{1},\sigma _{2}$
). The group of spherical twists is isomorphic to the 3-strand braid group
 $B_{3} = B_{A_2}$
, inducing a (weak) braid group action on
$B_{3} = B_{A_2}$
, inducing a (weak) braid group action on
 $\mathcal {C}_{2}$
(see [Reference Khovanov and Seidel10] and [Reference Seidel and Thomas18] for details). Let
$\mathcal {C}_{2}$
(see [Reference Khovanov and Seidel10] and [Reference Seidel and Thomas18] for details). Let
 $\mathbb {S}$
be the set of isomophism classes of spherical objects of
$\mathbb {S}$
be the set of isomophism classes of spherical objects of
 $\mathcal {C}_2$
. It is known that
$\mathcal {C}_2$
. It is known that
 $B_{3}$
acts transitively on this set; see, for example, [Reference Bapat, Deopurkar and Licata3, Theorem 1.1].
$B_{3}$
acts transitively on this set; see, for example, [Reference Bapat, Deopurkar and Licata3, Theorem 1.1].
4.2 Standard stability conditions on
 $\mathcal {C}_{2}$
$\mathcal {C}_{2}$
The proofs in the following section use a choice of a stability condition on
![]() $\mathcal {C}_2$
. Any choice will work, but for convenience, we choose a degenerate standard stability condition, defined as follows.
$\mathcal {C}_2$
. Any choice will work, but for convenience, we choose a degenerate standard stability condition, defined as follows.
Definition 4.1. A stability condition
![]() ${\tau }=(\mathcal {P}, Z)$
is standard if
${\tau }=(\mathcal {P}, Z)$
is standard if
![]() $\mathcal {P}([\phi ,\phi +1))=\heartsuit _{\operatorname {\mathrm {std}}}$
for some
$\mathcal {P}([\phi ,\phi +1))=\heartsuit _{\operatorname {\mathrm {std}}}$
for some
![]() $\phi \in \mathbb {R}$
. A standard stability condition
$\phi \in \mathbb {R}$
. A standard stability condition
![]() ${\tau }$
is degenerate if the phase of
${\tau }$
is degenerate if the phase of
![]() $P_1$
is equal to the phase of
$P_1$
is equal to the phase of
![]() $P_2$
.
$P_2$
.
Since
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are simple in
$P_2$
are simple in
![]() $\heartsuit _{\operatorname {\mathrm {std}}}$
, they are automatically stable in any standard stability condition. In a degenerate standard stability condition, the objects
$\heartsuit _{\operatorname {\mathrm {std}}}$
, they are automatically stable in any standard stability condition. In a degenerate standard stability condition, the objects
![]() $P_{12}$
and
$P_{12}$
and
![]() $P_{21}$
are also semistable of the same phase.
$P_{21}$
are also semistable of the same phase.
We will use the following proposition. It is a serious result, and corresponding versions of this proposition are true for any 2-Calabi–Yau category of a finite ADE type quiver. Several proofs of versions of this proposition are known, in various levels of generality: see, for example, [Reference Ishii, Ueda and Uehara9, Theorem 1], [Reference Ikeda7, Proposition 4.13], [Reference Adachi, Mizuno and Yang1, Corollary 9.5], [Reference Bapat, Deopurkar and Licata3, Theorem 1.2].
Proposition 4.2.
-
1. The space
 $\operatorname {\mathrm {Stab}}(\mathcal {C}_2)$
is connected.
$\operatorname {\mathrm {Stab}}(\mathcal {C}_2)$
is connected. -
2. For any stability condition
 ${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})$
, there exists a braid
${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})$
, there exists a braid
 ${\beta } \in B_{3}$
such that
${\beta } \in B_{3}$
such that
 ${\beta } {\tau }$
is a standard stability condition.
${\beta } {\tau }$
is a standard stability condition.
From now on, we fix a degenerate standard stability condition
![]() $\tau $
. The spherical objects in
$\tau $
. The spherical objects in
![]() $\mathcal {C}_{2}$
admit a simple classification based on their
$\mathcal {C}_{2}$
admit a simple classification based on their
![]() ${\tau }$
-HN filtration factors. This classification will be a key tool in later proofs. Given a set
${\tau }$
-HN filtration factors. This classification will be a key tool in later proofs. Given a set
![]() $S \subset \operatorname {\mathrm {Ob}} \mathcal {C}_2$
, let [
$S \subset \operatorname {\mathrm {Ob}} \mathcal {C}_2$
, let [
![]() $s\, |\, s \in S$
] denote the set of all objects of
$s\, |\, s \in S$
] denote the set of all objects of
![]() $\mathcal {C}_2$
whose
$\mathcal {C}_2$
whose
![]() $\tau $
-HN filtration factors consist of shifted copies of elements of S. For example,
$\tau $
-HN filtration factors consist of shifted copies of elements of S. For example,
![]() $[P_1,P_{12}]$
consists of all objects whose
$[P_1,P_{12}]$
consists of all objects whose
![]() $\tau $
-HN filtration factors are shifts of either
$\tau $
-HN filtration factors are shifts of either
![]() $P_1$
or
$P_1$
or
![]() $P_{12}$
.
$P_{12}$
.
The following proposition is similar to [Reference Bapat, Deopurkar and Licata2, Proposition 5.8].
Proposition 4.3. For each spherical object
![]() $X \in \mathbb {S}$
, one of the following is true:
$X \in \mathbb {S}$
, one of the following is true:
-
1.
 $X \in [P_{2}, P_{21}],$
$X \in [P_{2}, P_{21}],$
-
2.
 $X \in [P_{21}, P_{1}],$
$X \in [P_{21}, P_{1}],$
-
3.
 $X \in [P_{1}, P_{12}],$
$X \in [P_{1}, P_{12}],$
-
4.
 $X \in [P_{12}, P_{2}]$
.
$X \in [P_{12}, P_{2}]$
.
4.3 An automaton for the category
 $\mathcal {C}_2$
$\mathcal {C}_2$
In this section, we write down an explicit HN automaton for
![]() $\mathcal {C}_2$
(see Definition 3.4). In the next section, we discuss its implications on the dynamics of the braid group action on spherical objects of
$\mathcal {C}_2$
(see Definition 3.4). In the next section, we discuss its implications on the dynamics of the braid group action on spherical objects of
![]() $\mathcal {C}_2$
. Once again, fix
$\mathcal {C}_2$
. Once again, fix
![]() ${\tau }$
to be a degenerate standard stability condition. To construct a
${\tau }$
to be a degenerate standard stability condition. To construct a
![]() $\tau $
-HN automaton for
$\tau $
-HN automaton for
![]() $\mathcal {C}_2$
, we specify the following pieces of data.
$\mathcal {C}_2$
, we specify the following pieces of data.
-
1. Fig. 6 simultaneously depicts a
 $B_3$
-labelled graph
$B_3$
-labelled graph
 $\Theta $
and a
$\Theta $
and a
 $\Theta $
-set
$\Theta $
-set
 $\underline {S}\subset \underline {\operatorname {\mathrm {Ob}} C_2}$
.
$\underline {S}\subset \underline {\operatorname {\mathrm {Ob}} C_2}$
.
Figure 6 A
 $B_3$
-labelled graph
$B_3$
-labelled graph
 $\Theta $
, together with an assignment of a subset of
$\Theta $
, together with an assignment of a subset of
 $\operatorname {\mathrm {Ob}} \mathcal {C}_2$
to each vertex.
$\operatorname {\mathrm {Ob}} \mathcal {C}_2$
to each vertex. -
2. Fig. 7 depicts a
 $\Theta $
-representation
$\Theta $
-representation
 $\underline {M}$
. As shown in Fig. 6, the set at every vertex has the form
$\underline {M}$
. As shown in Fig. 6, the set at every vertex has the form
 $[A,B]$
, where
$[A,B]$
, where
 $A,B\in \Sigma _{\tau }$
. The summands in the module
$A,B\in \Sigma _{\tau }$
. The summands in the module
 $\mathbb {Z}[q^{\pm }]^2 = \mathbb {Z}[q^{\pm }] \oplus \mathbb {Z}[q^{\pm }]$
at that vertex should be thought of as being indexed by A and B, respectively.
$\mathbb {Z}[q^{\pm }]^2 = \mathbb {Z}[q^{\pm }] \oplus \mathbb {Z}[q^{\pm }]$
at that vertex should be thought of as being indexed by A and B, respectively.
Figure 7 A
 $ \Theta $
-representation
$ \Theta $
-representation
 $ \underline {M}$
.
$ \underline {M}$
. -
3. The morphism
 $i \colon \underline {S} \to \underline {M}$
is as follows. At each vertex, the map
$i \colon \underline {S} \to \underline {M}$
is as follows. At each vertex, the map
 $[A,B] \to \mathbb {Z}[q^{\pm }]^2$
takes an object
$[A,B] \to \mathbb {Z}[q^{\pm }]^2$
takes an object
 $X \in [A,B]$
to the A and B coordinates of
$X \in [A,B]$
to the A and B coordinates of
 $\operatorname {\mathrm {HN}}_{\tau }(X)$
. The proof that i is
$\operatorname {\mathrm {HN}}_{\tau }(X)$
. The proof that i is
 $\Theta $
-equivariant is a calculation that proceeds exactly as in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.1].
$\Theta $
-equivariant is a calculation that proceeds exactly as in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.1]. -
4. Finally,
 $h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
is simply the inclusion map. We need to check that for any vertex v and any
$h_v \colon M_v \to \mathbb {Z}[q^{\pm }]^{\Sigma _{\tau }}$
is simply the inclusion map. We need to check that for any vertex v and any
 $X \in S_v$
, we have
$X \in S_v$
, we have  $$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X) = h_v(i_v(X)).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{HN}}_{\tau}(X) = h_v(i_v(X)).\end{align*}$$
In other words, we check that the
 $\tau $
-HN multiplicity vectors transform according to matrices in Fig. 7. This check, which is involved, is essentially identical to the one done in [Reference Bapat, Deopurkar and Licata2, Proposition 5.1]. We omit the details here.
$\tau $
-HN multiplicity vectors transform according to matrices in Fig. 7. This check, which is involved, is essentially identical to the one done in [Reference Bapat, Deopurkar and Licata2, Proposition 5.1]. We omit the details here.
4.4 The dynamics of the braid group action on spherical objects
We now define two kinds of functionals
![]() $\mathbb {S}\times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
. The first of these is an extension of a functional
$\mathbb {S}\times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
. The first of these is an extension of a functional
![]() $\{P_{1},P_{2}\}\times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
that counts the ‘occurrences’ of the building block complexes
$\{P_{1},P_{2}\}\times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
that counts the ‘occurrences’ of the building block complexes
![]() $P_{2}$
and
$P_{2}$
and
![]() $P_{1}$
, respectively, in a complex
$P_{1}$
, respectively, in a complex
![]() $X \in \mathbb {S}$
. We continue to denote by
$X \in \mathbb {S}$
. We continue to denote by
![]() ${\tau }$
a degenerate standard stability condition on
${\tau }$
a degenerate standard stability condition on
![]() $\mathcal {C}_{2}$
.
$\mathcal {C}_{2}$
.
We know that in this case, the set of indecomposable semistable objects in the heart is just
With these coordinates, for any
![]() $X \in \mathcal {T}$
, we write
$X \in \mathcal {T}$
, we write
![]() $\operatorname {\mathrm {HN}}_{\tau }(X)$
as
$\operatorname {\mathrm {HN}}_{\tau }(X)$
as
Definition 4.4. We define functionals
![]() $\mathbb {S} \times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
as follows. For any
$\mathbb {S} \times \mathbb {S} \to \mathbb {Z}[q^{\pm }]$
as follows. For any
![]() $X \in \mathbb {S}$
,
$X \in \mathbb {S}$
,
 $$ \begin{align*} \operatorname{\mathrm{occ}}_{q}(P_{1}, X)&:=\pi_{2}(X)+\pi_{12}(X)+\pi_{21}(X),\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, X)&:=\pi_{1}(X)+\pi_{12}(X)+\pi_{21}(X). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{occ}}_{q}(P_{1}, X)&:=\pi_{2}(X)+\pi_{12}(X)+\pi_{21}(X),\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, X)&:=\pi_{1}(X)+\pi_{12}(X)+\pi_{21}(X). \end{align*} $$
For any
![]() $X,Y \in \mathbb {S}$
, let
$X,Y \in \mathbb {S}$
, let
![]() $X={\beta } P_{1}$
, then
$X={\beta } P_{1}$
, then
Remark 4.5. Note that
![]() $\operatorname {\mathrm {occ}}_{q}(P_{1},X)$
counts the ‘occurrences’ of
$\operatorname {\mathrm {occ}}_{q}(P_{1},X)$
counts the ‘occurrences’ of
![]() $P_{2}$
in X and vice versa, which is notationally confusing but somewhat unavoidable. Every occurrence of
$P_{2}$
in X and vice versa, which is notationally confusing but somewhat unavoidable. Every occurrence of
![]() $P_{2}$
in X must correspond to an HN filtration factor of the form
$P_{2}$
in X must correspond to an HN filtration factor of the form
![]() $P_{2}$
,
$P_{2}$
,
![]() $P_{12}$
or
$P_{12}$
or
![]() $P_{21}$
, up to shift. Thus, summing the number of these factors, with degree, gives the number of
$P_{21}$
, up to shift. Thus, summing the number of these factors, with degree, gives the number of
![]() $P_{2}$
’s, with degree.
$P_{2}$
’s, with degree.
Definition 4.6. The functional
![]() $\operatorname {\mathrm {occ}}_{q}$
has a close cousin,
$\operatorname {\mathrm {occ}}_{q}$
has a close cousin,
![]() $\overline {\hom }_{q}$
:
$\overline {\hom }_{q}$
:
 $$ \begin{align*}\overline{\hom}_{q}(X,Y):=\begin{cases} q^{n}(q^{-2}-q^{-1}), & Y\cong X[n],\\ \sum_{n \in \mathbb{Z}}\dim_{{\Bbbk}}\operatorname{\mathrm{Hom}}(X,Y[n])q^{-n}, & \text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}\overline{\hom}_{q}(X,Y):=\begin{cases} q^{n}(q^{-2}-q^{-1}), & Y\cong X[n],\\ \sum_{n \in \mathbb{Z}}\dim_{{\Bbbk}}\operatorname{\mathrm{Hom}}(X,Y[n])q^{-n}, & \text{otherwise.} \end{cases}\end{align*} $$
The following theorems relate these functionals to the q-deformed rational numbers. For reasons that will soon be obvious, for any
![]() $X \in \mathbb {S}$
, we write
$X \in \mathbb {S}$
, we write
![]() $X\geq 0$
to mean
$X\geq 0$
to mean
![]() $X \in [P_{2}, P_{21}]\cup [P_{21}, P_{1}]$
and
$X \in [P_{2}, P_{21}]\cup [P_{21}, P_{1}]$
and
![]() $X \leq 0$
to mean
$X \leq 0$
to mean
![]() $X \in [P_{1}, P_{12}]\cup [P_{12}, P_{2}]$
.
$X \in [P_{1}, P_{12}]\cup [P_{12}, P_{2}]$
.
Theorem 4.7. For every
![]() $X \in \mathbb {S}$
,
$X \in \mathbb {S}$
,
 $$ \begin{align*}(-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_{q}(P_{2},X)}{\operatorname{\mathrm{occ}}_{q}(P_{1},X)}\end{align*} $$
$$ \begin{align*}(-q)^{-\epsilon}\frac{\operatorname{\mathrm{occ}}_{q}(P_{2},X)}{\operatorname{\mathrm{occ}}_{q}(P_{1},X)}\end{align*} $$
is a right q-deformed rational number, where
 $$ \begin{align*}\epsilon=\begin{cases} 0, & X\geq 0,\\ 1, & X\leq0.\end{cases}\end{align*} $$
$$ \begin{align*}\epsilon=\begin{cases} 0, & X\geq 0,\\ 1, & X\leq0.\end{cases}\end{align*} $$
Moreover, the induced map from
![]() $\mathbb {S}$
to the set of q-deformed rationals is
$\mathbb {S}$
to the set of q-deformed rationals is
![]() $B_{3}$
-equivariant and bijective (up to shift).
$B_{3}$
-equivariant and bijective (up to shift).
Theorem 4.8. For every
![]() $X \in \mathbb {S}$
,
$X \in \mathbb {S}$
,
 $$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*} $$
$$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*} $$
is a left q-deformed rational number, where
 $$ \begin{align*}\epsilon=\begin{cases} 0, & X\geq0, X \not\cong P_{2}[n],\\ 1, & X\leq 0, X \not\cong P_{1}[n].\end{cases}\end{align*} $$
$$ \begin{align*}\epsilon=\begin{cases} 0, & X\geq0, X \not\cong P_{2}[n],\\ 1, & X\leq 0, X \not\cong P_{1}[n].\end{cases}\end{align*} $$
Moreover, the induced map from
![]() $\mathbb {S}$
to the set of left q-deformed rationals is
$\mathbb {S}$
to the set of left q-deformed rationals is
![]() $B_{3}$
-equivariant and bijective (up to shift).
$B_{3}$
-equivariant and bijective (up to shift).
These theorems were first proven in the case
![]() $q=1$
, where they are identical, by Rouquier and Zimmermann [Reference Rouquier and Zimmermann17, Proposition 4.8]. The proofs of these theorems for arbitrary q will occupy the rest of this section. In [Reference Bapat, Deopurkar and Licata2, Proposition 5.10], a proof of the original Rouquier–Zimmermann bijection is established using the theory of Harder–Narasimhan automata; it is this proof technique that we adapt to prove the above theorems. More precisely, to prove Theorem 4.7, we will use the automaton introduced in Section 4.3 to analyse the dynamics of spherical objects in
$q=1$
, where they are identical, by Rouquier and Zimmermann [Reference Rouquier and Zimmermann17, Proposition 4.8]. The proofs of these theorems for arbitrary q will occupy the rest of this section. In [Reference Bapat, Deopurkar and Licata2, Proposition 5.10], a proof of the original Rouquier–Zimmermann bijection is established using the theory of Harder–Narasimhan automata; it is this proof technique that we adapt to prove the above theorems. More precisely, to prove Theorem 4.7, we will use the automaton introduced in Section 4.3 to analyse the dynamics of spherical objects in
![]() $\mathcal {C}_{2}$
under the braid group action.
$\mathcal {C}_{2}$
under the braid group action.
The proof of Theorem 4.7 will proceed by an induction on the length of elements of
![]() $B_{3}$
. To facilitate this induction, we introduce a normal form for the three-strand braid group
$B_{3}$
. To facilitate this induction, we introduce a normal form for the three-strand braid group
![]() $B_{3}$
, which is (mostly) recognised by the automaton (that is, for every braid we will need in the proof, there is a path along the edges of the automaton given by its continued normal form). Let
$B_{3}$
, which is (mostly) recognised by the automaton (that is, for every braid we will need in the proof, there is a path along the edges of the automaton given by its continued normal form). Let
![]() $\omega :=\sigma _{2}\sigma _{1}\sigma _{2}\sigma _{1}\sigma _{2}\sigma _{1}$
be the generator of the centre of
$\omega :=\sigma _{2}\sigma _{1}\sigma _{2}\sigma _{1}\sigma _{2}\sigma _{1}$
be the generator of the centre of
![]() $B_{3}$
,
$B_{3}$
,
Lemma 4.9 (Continued normal form).
Consider any braid
![]() ${\beta } \in B_{3}$
. We can write
${\beta } \in B_{3}$
. We can write
![]() ${\beta }$
uniquely in one of four forms, determined by the image of
${\beta }$
uniquely in one of four forms, determined by the image of
![]() $P_{1}$
:
$P_{1}$
:

where
![]() $a_{1} \in \mathbb {N}$
,
$a_{1} \in \mathbb {N}$
,
![]() $a_{2},\ldots ,a_{2n} \in \mathbb {N}\setminus 0$
,
$a_{2},\ldots ,a_{2n} \in \mathbb {N}\setminus 0$
,
![]() $M,N \in \mathbb {Z}$
.
$M,N \in \mathbb {Z}$
.
Taking
![]() $P_{1}$
as the counterpart of
$P_{1}$
as the counterpart of
![]() $\infty $
and
$\infty $
and
![]() $P_{2}$
as the counterpart of 0, Lemma 4.9 corresponds exactly to the continued fraction expansion in Section 2.1.
$P_{2}$
as the counterpart of 0, Lemma 4.9 corresponds exactly to the continued fraction expansion in Section 2.1.
Proof. Consider any braid
![]() ${\beta } \in B_{3}$
. Let
${\beta } \in B_{3}$
. Let
![]() $\overline {{\beta }}$
denote the corresponding element of
$\overline {{\beta }}$
denote the corresponding element of
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
(under the standard surjection
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
(under the standard surjection
![]() $B_{3} \to \operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
.) Let
$B_{3} \to \operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
.) Let
![]() $\overline {{\beta }}\big [\begin {smallmatrix}1 \\ 0 \end {smallmatrix}\big ]=\big [\begin {smallmatrix} r \\ s \end {smallmatrix}\big ]$
. Then, by Proposition 2.2, there exists a matrix
$\overline {{\beta }}\big [\begin {smallmatrix}1 \\ 0 \end {smallmatrix}\big ]=\big [\begin {smallmatrix} r \\ s \end {smallmatrix}\big ]$
. Then, by Proposition 2.2, there exists a matrix
![]() $\overline {{\beta }'}$
of the form
$\overline {{\beta }'}$
of the form
such that
![]() $\overline {{\beta }'}\big [\begin {smallmatrix} 1 \\ 0 \end {smallmatrix}\big ]=\big [\begin {smallmatrix} r \\ s \end {smallmatrix}\big ]$
. Since
$\overline {{\beta }'}\big [\begin {smallmatrix} 1 \\ 0 \end {smallmatrix}\big ]=\big [\begin {smallmatrix} r \\ s \end {smallmatrix}\big ]$
. Since
![]() $\overline {{\beta }'}$
and
$\overline {{\beta }'}$
and
![]() $\overline {{\beta }}$
act identically on
$\overline {{\beta }}$
act identically on
![]() $\big [\begin {smallmatrix} 1 \\ 0 \end {smallmatrix}\big ]$
, we have that
$\big [\begin {smallmatrix} 1 \\ 0 \end {smallmatrix}\big ]$
, we have that
![]() $\overline {{\beta }'}=\overline {{\beta }}\overline {\sigma }_{1}^{M}$
for some
$\overline {{\beta }'}=\overline {{\beta }}\overline {\sigma }_{1}^{M}$
for some
![]() $M \in \mathbb {Z}$
(this can be deduced from the fact that every matrix in
$M \in \mathbb {Z}$
(this can be deduced from the fact that every matrix in
![]() $\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
has determinant 1). Lemma 4.9 then follows from the fact that the kernel of
$\operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
has determinant 1). Lemma 4.9 then follows from the fact that the kernel of
![]() $B_{3} \to \operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
is the centre
$B_{3} \to \operatorname {\mathrm {PSL}}_{2}(\mathbb {Z})$
is the centre
![]() $Z(B_{3})$
.
$Z(B_{3})$
.
If
![]() ${\beta }$
is given by the form in Lemma 4.9, we say that
${\beta }$
is given by the form in Lemma 4.9, we say that
![]() ${\beta }$
is written in ‘(even) continued form’. We say that
${\beta }$
is written in ‘(even) continued form’. We say that
![]() ${\beta }$
is written in ‘strict continued form’ if any of the following hold:
${\beta }$
is written in ‘strict continued form’ if any of the following hold:
-
1.
 ${\beta }$
is written in form (4.1),
${\beta }$
is written in form (4.1),
 $M \leq 0$
;
$M \leq 0$
; -
2.
 ${\beta }$
is written in form (4.2),
${\beta }$
is written in form (4.2),
 $M \geq 0$
;
$M \geq 0$
; -
3.
 ${\beta }$
is written in form (4.3);
${\beta }$
is written in form (4.3); -
4.
 ${\beta }$
is written in form (4.4),
${\beta }$
is written in form (4.4),
 $M\leq 0$
.
$M\leq 0$
.
The following corollary of Lemma 4.9 follows from the calculation:
Corollary 4.10 (Strict continued normal form).
For any
![]() $X \in \mathbb {S}$
, there exists a braid
$X \in \mathbb {S}$
, there exists a braid
![]() ${\beta }$
in strict continued form such that
${\beta }$
in strict continued form such that
![]() ${\beta } P_{1}=X$
.
${\beta } P_{1}=X$
.
Theorem 4.7 is an immediate corollary of the matrix formula for right q-rationals (Proposition 2.11) and the following Propositions 4.11 and 4.12:
Proposition 4.11. Consider any
![]() ${\beta } \in B_{3}$
which can be written in strict continued form, and let
${\beta } \in B_{3}$
which can be written in strict continued form, and let
![]() $\overline {{\beta }}$
be the corresponding q-deformed matrix. Up to multiplication by
$\overline {{\beta }}$
be the corresponding q-deformed matrix. Up to multiplication by
![]() $-1$
and by powers of q, we have an equality:
$-1$
and by powers of q, we have an equality:
 $$ \begin{align*}\overline{{\beta}}= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{1}) & (-q)^{-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{2}) \\ (-q)^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{2}) \end{bmatrix}, \end{align*} $$
$$ \begin{align*}\overline{{\beta}}= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{1}) & (-q)^{-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{2}) \\ (-q)^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{2}) \end{bmatrix}, \end{align*} $$
where
 $$ \begin{align*}\epsilon=\begin{cases} 0, & {\beta} P_{2}\geq 0, \\ 1, & {\beta} P_{2}\leq 0. \end{cases}\end{align*} $$
$$ \begin{align*}\epsilon=\begin{cases} 0, & {\beta} P_{2}\geq 0, \\ 1, & {\beta} P_{2}\leq 0. \end{cases}\end{align*} $$
Proposition 4.12. Consider any
![]() ${\beta } \in B_{3}$
which cannot be written in strict continued form. Then, up to multiplication by
${\beta } \in B_{3}$
which cannot be written in strict continued form. Then, up to multiplication by
![]() $-1$
and by powers of q, we have:
$-1$
and by powers of q, we have:
 $$ \begin{align*}\overline{{\beta}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{1}) & (-q)^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1},{\beta} P_{1} ) & (-q)^{2 \epsilon -1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{2}) \end{bmatrix} \end{align*} $$
$$ \begin{align*}\overline{{\beta}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{1}) & (-q)^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1},{\beta} P_{1} ) & (-q)^{2 \epsilon -1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta} P_{2}) \end{bmatrix} \end{align*} $$
where
 $$ \begin{align*}\epsilon=\begin{cases} 0, & {\beta} P_{2}\geq 0, \\ 1, & {\beta} P_{2} \leq 0. \end{cases}\end{align*} $$
$$ \begin{align*}\epsilon=\begin{cases} 0, & {\beta} P_{2}\geq 0, \\ 1, & {\beta} P_{2} \leq 0. \end{cases}\end{align*} $$
Proof of Proposition 4.11.
Consider any
![]() ${\beta } \in B_{3}$
which can be written in strict continued form. We induct on the length of
${\beta } \in B_{3}$
which can be written in strict continued form. We induct on the length of
![]() ${\beta }$
. The base case
${\beta }$
. The base case
![]() ${\beta }=\operatorname {\mathrm {Id}}$
is trivial. Since multiplication by
${\beta }=\operatorname {\mathrm {Id}}$
is trivial. Since multiplication by
![]() $\omega $
corresponds to scalar multiplication by a power of q, we can assume without loss of generality that the
$\omega $
corresponds to scalar multiplication by a power of q, we can assume without loss of generality that the
![]() $\omega ^{N}$
-term in
$\omega ^{N}$
-term in
![]() ${\beta }$
is trivial (i.e.,
${\beta }$
is trivial (i.e.,
![]() $N=0$
).
$N=0$
).
For the induction argument, note that
![]() ${\beta }$
, read from right to left, defines a path in
${\beta }$
, read from right to left, defines a path in
![]() $\Theta $
(Fig. 6). We will ignore the case that
$\Theta $
(Fig. 6). We will ignore the case that
![]() ${\beta }$
is in the forms (4.3) and (4.4) (in the notation of Lemma 4.9), since this can be easily done by hand.
${\beta }$
is in the forms (4.3) and (4.4) (in the notation of Lemma 4.9), since this can be easily done by hand.
Let
![]() ${\beta }_{l}$
be the braid consisting of the last l elementary braids in
${\beta }_{l}$
be the braid consisting of the last l elementary braids in
![]() ${\beta }$
, and suppose that
${\beta }$
, and suppose that
 $$ \begin{align*}\overline{{\beta}_{l}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & (-q^{-1})^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ (-q)^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix}\end{align*} $$
$$ \begin{align*}\overline{{\beta}_{l}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & (-q^{-1})^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ (-q)^{\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix}\end{align*} $$
There are eight cases, depending on whether
![]() ${\beta }$
has the form (4.1) or (4.2) in the notation of Lemma 4.9 and on the value of
${\beta }$
has the form (4.1) or (4.2) in the notation of Lemma 4.9 and on the value of
![]() ${\beta }_{l+1}{\beta }_{l}^{-1}$
. Note that
${\beta }_{l+1}{\beta }_{l}^{-1}$
. Note that
![]() ${\beta }_{l}P_{1} \in [P_{i}, P_{j}]$
if and only if
${\beta }_{l}P_{1} \in [P_{i}, P_{j}]$
if and only if
![]() ${\beta }_{l}P_{2} \in [P_{i}, P_{j}]$
. For illustrative purposes, we will assume that
${\beta }_{l}P_{2} \in [P_{i}, P_{j}]$
. For illustrative purposes, we will assume that
![]() ${\beta }$
has the form (4.1) (and thus
${\beta }$
has the form (4.1) (and thus
![]() $\epsilon =0$
), that
$\epsilon =0$
), that
![]() ${\beta }_{l}P_{1}, {\beta }_{l}P_{2}\in [P_{21}, P_{1}]$
and
${\beta }_{l}P_{1}, {\beta }_{l}P_{2}\in [P_{21}, P_{1}]$
and
![]() ${\beta }_{l+1}=\sigma _{2}{\beta }_{l}$
. First, we calculate
${\beta }_{l+1}=\sigma _{2}{\beta }_{l}$
. First, we calculate
 $$ \begin{align*} \overline{{\beta}_{l+1}}&=\overline{\sigma_{2}{\beta}_{l}} \\ &=\begin{bmatrix} 1 & 0 \\ 1 & q^{-1}\end{bmatrix}\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix} \\&=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1})+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2})+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix} \end{align*} $$
$$ \begin{align*} \overline{{\beta}_{l+1}}&=\overline{\sigma_{2}{\beta}_{l}} \\ &=\begin{bmatrix} 1 & 0 \\ 1 & q^{-1}\end{bmatrix}\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix} \\&=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1})+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2})+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}). \end{bmatrix} \end{align*} $$
However, by definition, we have equalities
 $$ \begin{align*} \begin{bmatrix} \pi_{21}({\beta}_{l}P_{1}) & \pi_{21}({\beta}_{l}P_{2}) \\ \pi_{1}({\beta}_{l}P_{1}) & \pi_{1}({\beta}_{l}P_{2}) \end{bmatrix}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{1})-\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{2})-\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{2}) \end{bmatrix} \end{align*} $$
$$ \begin{align*} \begin{bmatrix} \pi_{21}({\beta}_{l}P_{1}) & \pi_{21}({\beta}_{l}P_{2}) \\ \pi_{1}({\beta}_{l}P_{1}) & \pi_{1}({\beta}_{l}P_{2}) \end{bmatrix}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{1})-\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{2})-\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{2}) \end{bmatrix} \end{align*} $$
and
 $$ \begin{align}\begin{split} &\begin{bmatrix} \pi_{2}({\beta}_{l+1}P_{1}) & \pi_{2}({\beta}_{l+1}P_{2}) \\ \pi_{21}({\beta}_{l+1}P_{1})& \pi_{21}({\beta}_{l+1}P_{2}) \end{bmatrix}\\&=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{1})-\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{2})-\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{2}) \end{bmatrix}\end{split} \end{align} $$
$$ \begin{align}\begin{split} &\begin{bmatrix} \pi_{2}({\beta}_{l+1}P_{1}) & \pi_{2}({\beta}_{l+1}P_{2}) \\ \pi_{21}({\beta}_{l+1}P_{1})& \pi_{21}({\beta}_{l+1}P_{2}) \end{bmatrix}\\&=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{1})-\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{2})-\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{2}) \end{bmatrix}\end{split} \end{align} $$
Applying the linear representation embedded in
![]() $\Theta $
,
$\Theta $
,
 $$ \begin{align}\begin{split} \begin{bmatrix} \pi_{2}({\beta}_{l+1}P_{1}) & \pi_{2}({\beta}_{l+1}P_{2}) \\ \pi_{21}({\beta}_{l+1}P_{1}) & \pi_{21}({\beta}_{l+1}P_{2}) \end{bmatrix} &=\begin{bmatrix} q^{-1} & 0 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \pi_{21}({\beta}_{l}P_{1}) & \pi_{21}({\beta}_{l}P_{2}) \\ \pi_{1}({\beta}_{l}P_{1}) & \pi_{1}({\beta}_{l}P_{2}) \end{bmatrix}\\& =\begin{bmatrix} q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \end{bmatrix}\end{split} \end{align} $$
$$ \begin{align}\begin{split} \begin{bmatrix} \pi_{2}({\beta}_{l+1}P_{1}) & \pi_{2}({\beta}_{l+1}P_{2}) \\ \pi_{21}({\beta}_{l+1}P_{1}) & \pi_{21}({\beta}_{l+1}P_{2}) \end{bmatrix} &=\begin{bmatrix} q^{-1} & 0 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \pi_{21}({\beta}_{l}P_{1}) & \pi_{21}({\beta}_{l}P_{2}) \\ \pi_{1}({\beta}_{l}P_{1}) & \pi_{1}({\beta}_{l}P_{2}) \end{bmatrix}\\& =\begin{bmatrix} q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{1}) & q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l} P_{2}) \end{bmatrix}\end{split} \end{align} $$
Comparing Eq. (4.5) and Eq. (4.6) gives us that for
![]() $i \in \{1,2\}$
,
$i \in \{1,2\}$
,
 $$ \begin{align*} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{i})&=\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{i}),\\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{i})&=q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{i}) +\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{i}), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1}P_{i})&=\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{i}),\\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1}P_{i})&=q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l}P_{i}) +\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l}P_{i}), \end{align*} $$
which proves that
 $$ \begin{align*}\overline{{\beta}_{l+1}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1} P_{2}). \end{bmatrix}.\end{align*} $$
$$ \begin{align*}\overline{{\beta}_{l+1}}=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}_{l+1} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}_{l+1} P_{2}). \end{bmatrix}.\end{align*} $$
Verifying the other seven cases (using the exact same procedure) completes the induction argument.
The proof of Propositon 4.12 is virtually the same as the proof of Proposition 4.11. Any braid which cannot be written in strictly normal form can be obtained from one that can, by multiplying on the right by
![]() $\sigma _{1}^{M}$
. Thus, one can prove this case using the same method as in part 1, but changing the base case appropriately.
$\sigma _{1}^{M}$
. Thus, one can prove this case using the same method as in part 1, but changing the base case appropriately.
This completes the proof of Theorem 4.7.
A proof of Theorem 4.8 can be constructed independently, analogously to the above proof. In lieu of doing that, we will bootstrap Theorem 4.8 to Theorem 4.7 by way of the following relationship between
![]() $\operatorname {\mathrm {occ}}_{q}$
and
$\operatorname {\mathrm {occ}}_{q}$
and
![]() $\overline {\hom }_{q}$
:
$\overline {\hom }_{q}$
:
Lemma 4.13 (
 $\hom $
-values).
$\hom $
-values).
The functional
![]() $\overline {\hom }_{q}(P_{1},-)$
takes the following values:
$\overline {\hom }_{q}(P_{1},-)$
takes the following values:
 $$ \begin{align*}\overline{\hom}_{q}(P_{1},X)=\begin{cases} (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X), & X \geq 0\\ (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X), & X \leq 0. \end{cases}\end{align*} $$
$$ \begin{align*}\overline{\hom}_{q}(P_{1},X)=\begin{cases} (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X), & X \geq 0\\ (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X), & X \leq 0. \end{cases}\end{align*} $$
Symmetrically, the functional
![]() $\overline {\hom }_{q}(P_{2}, -)$
takes the following values:
$\overline {\hom }_{q}(P_{2}, -)$
takes the following values:
 $$ \begin{align*}\overline{\hom}_{q}(P_{2},X)=\begin{cases} (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{1},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2},X), & X\geq 0, \\ (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{1},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2},X), & X \leq 0. \end{cases}\end{align*} $$
$$ \begin{align*}\overline{\hom}_{q}(P_{2},X)=\begin{cases} (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{1},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2},X), & X\geq 0, \\ (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{1},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2},X), & X \leq 0. \end{cases}\end{align*} $$
Proof of Theorem 4.8.
Consider any
![]() $X \in \mathbb {S}$
. Assume that
$X \in \mathbb {S}$
. Assume that
![]() $X \neq P_{1},P_{2}$
. By Corollary 4.10, we can write
$X \neq P_{1},P_{2}$
. By Corollary 4.10, we can write
![]() $X={\beta } P_{1}$
for some
$X={\beta } P_{1}$
for some
![]() ${\beta }$
in strict continued form. It is easy to check that
${\beta }$
in strict continued form. It is easy to check that
![]() ${\beta } P_{1}\geq 0$
implies
${\beta } P_{1}\geq 0$
implies
![]() ${\beta }^{-1} P_{1} \leq 0$
(and vice versa), and thus, by Proposition 4.11, we have the following equality (up to scaling):
${\beta }^{-1} P_{1} \leq 0$
(and vice versa), and thus, by Proposition 4.11, we have the following equality (up to scaling):
 $$ \begin{align*} \overline{{\beta}}&=\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) & (-q)^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-q)^{1-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2})\end{bmatrix}^{-1}\\ &=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2}) & (-1)^{\epsilon}q^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \overline{{\beta}}&=\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) & (-q)^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-q)^{1-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2})\end{bmatrix}^{-1}\\ &=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2}) & (-1)^{\epsilon}q^{\epsilon-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) & \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) \end{bmatrix}. \end{align*} $$
Let
![]() $\mathcal {R}^{\flat }(q)/\mathcal {S}^{\flat }(q)$
be the rational function representation of
$\mathcal {R}^{\flat }(q)/\mathcal {S}^{\flat }(q)$
be the rational function representation of
![]() $[{\beta }(\infty )]_{q}^{\flat }$
, using the notation in Definition 2.7. Combining the matrix formula for right q-rationals (Proposition 2.11) and the
$[{\beta }(\infty )]_{q}^{\flat }$
, using the notation in Definition 2.7. Combining the matrix formula for right q-rationals (Proposition 2.11) and the
![]() $\hom $
-values lemma (Lemma 4.13), we have (again up to scaling):
$\hom $
-values lemma (Lemma 4.13), we have (again up to scaling):
 $$ \begin{align*} \begin{bmatrix} \mathcal{R}^{\flat}(q) \\ \mathcal{S}^{\flat}(q) \end{bmatrix} &= \overline{{\beta}}\begin{bmatrix}q^{-1}\\ q^{-1}-1 \end{bmatrix} \\ &=\begin{bmatrix} q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2}) +(-1)^{\epsilon}(q^{\epsilon-2}-q^{\epsilon-1})\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-1)^{\epsilon}q^{-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) +(q^{-1}-1)\operatorname{\mathrm{occ}}_{q} (P_{2}, {\beta}^{-1} P_{1}) \end{bmatrix} \\&=\begin{bmatrix} \overline{\hom}_{q}(P_{1}, {\beta}^{-1}P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\overline{\hom}_{q}(P_{1}, {\beta}^{-1}P_{1}) \end{bmatrix} \\ &=\begin{bmatrix} \overline{\hom}_{q}(X, P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\overline{\hom}_{q}(X,P_{1}) \end{bmatrix} \end{align*} $$
$$ \begin{align*} \begin{bmatrix} \mathcal{R}^{\flat}(q) \\ \mathcal{S}^{\flat}(q) \end{bmatrix} &= \overline{{\beta}}\begin{bmatrix}q^{-1}\\ q^{-1}-1 \end{bmatrix} \\ &=\begin{bmatrix} q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{2}) +(-1)^{\epsilon}(q^{\epsilon-2}-q^{\epsilon-1})\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{2}) \\ (-1)^{\epsilon}q^{-\epsilon}\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) +(q^{-1}-1)\operatorname{\mathrm{occ}}_{q} (P_{2}, {\beta}^{-1} P_{1}) \end{bmatrix} \\&=\begin{bmatrix} \overline{\hom}_{q}(P_{1}, {\beta}^{-1}P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\overline{\hom}_{q}(P_{1}, {\beta}^{-1}P_{1}) \end{bmatrix} \\ &=\begin{bmatrix} \overline{\hom}_{q}(X, P_{2}) \\ (-1)^{\epsilon}q^{1-\epsilon}\overline{\hom}_{q}(X,P_{1}) \end{bmatrix} \end{align*} $$
This shows that
 $$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*} $$
$$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}(X,P_{2})}{\overline{\hom}_{q}(X,P_{1})}\end{align*} $$
is indeed a left q-deformed rational number and that the map sending
![]() ${\beta } P_{1}$
to
${\beta } P_{1}$
to
![]() $[{\beta }(\infty )]_{q}^{\flat }$
is a bijection.
$[{\beta }(\infty )]_{q}^{\flat }$
is a bijection.
We now prove
![]() $B_{3}$
-equivariance. By construction, we have that for every
$B_{3}$
-equivariance. By construction, we have that for every
![]() $X \in \mathbb {S}$
, there is some
$X \in \mathbb {S}$
, there is some
![]() ${\beta } \in B_{3}$
, such that
${\beta } \in B_{3}$
, such that
![]() $X={\beta } P_{1}$
and
$X={\beta } P_{1}$
and
 $$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}({\beta} P_{1},P_{2})}{\overline{\hom}_{q}({\beta} P_{1},P_{1})}={\beta}\frac{\overline{\hom}_{q}(P_{1},P_{2})}{\overline{\hom}_{q}(P_{1},P_{1})}={\beta} [\infty]_{q}^{\flat}.\end{align*} $$
$$ \begin{align*}(-1)^{\epsilon}q^{\epsilon-1}\frac{\overline{\hom}_{q}({\beta} P_{1},P_{2})}{\overline{\hom}_{q}({\beta} P_{1},P_{1})}={\beta}\frac{\overline{\hom}_{q}(P_{1},P_{2})}{\overline{\hom}_{q}(P_{1},P_{1})}={\beta} [\infty]_{q}^{\flat}.\end{align*} $$
Consider any
![]() ${\beta }_{1}, {\beta }_{2} \in B_{3}$
such that
${\beta }_{1}, {\beta }_{2} \in B_{3}$
such that
![]() ${\beta }_{1} P_{1}={\beta }_{2} P_{1}$
. To prove
${\beta }_{1} P_{1}={\beta }_{2} P_{1}$
. To prove
![]() $B_{3}$
-equivariance, it will be sufficient to show that
$B_{3}$
-equivariance, it will be sufficient to show that
![]() ${\beta }_{1}$
and
${\beta }_{1}$
and
![]() ${\beta }_{2}$
act identically on
${\beta }_{2}$
act identically on
![]() $[\infty ]_{q}^{\flat }$
. By elementary braid group arithmetic,
$[\infty ]_{q}^{\flat }$
. By elementary braid group arithmetic,
![]() ${\beta }_{1}={\beta }_{2}\sigma _{1}^{n}$
for some
${\beta }_{1}={\beta }_{2}\sigma _{1}^{n}$
for some
![]() $n \in \mathbb {Z}$
. Since
$n \in \mathbb {Z}$
. Since
![]() $\sigma _{1}$
fixes
$\sigma _{1}$
fixes
![]() $[\infty ]_{q}^{\flat }$
, we have that
$[\infty ]_{q}^{\flat }$
, we have that
This completes the proof of
![]() $B_{3}$
-equivariance.
$B_{3}$
-equivariance.
5 A family of compactifications of the space of Bridgeland stability conditions
The aim of this section is to propose a family of compactifications of the space of Bridgeland stability conditions of a triangulated category indexed by
![]() $q> 0$
. This construction generalises results of [Reference Bapat, Deopurkar and Licata2]. In particular, for each real number
$q> 0$
. This construction generalises results of [Reference Bapat, Deopurkar and Licata2]. In particular, for each real number
![]() $q>0$
, the corresponding compactification will be the closure of an embedding (via q-masses) of
$q>0$
, the corresponding compactification will be the closure of an embedding (via q-masses) of
![]() $\operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C}$
into a fixed infinite projective space. We prove and conjecture several properties of this construction for 2-CY categories associated to connected quivers and analyse the construction in detail for the category
$\operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C}$
into a fixed infinite projective space. We prove and conjecture several properties of this construction for 2-CY categories associated to connected quivers and analyse the construction in detail for the category
![]() $\mathcal {C}_2$
.
$\mathcal {C}_2$
.
5.1 The deformed mass embedding
Suppose that
![]() $\mathcal T$
is the 2-CY category associated to a connected quiver (we will specialise to
$\mathcal T$
is the 2-CY category associated to a connected quiver (we will specialise to
![]() $\mathcal {C}_{2}$
again shortly). Let
$\mathcal {C}_{2}$
again shortly). Let
![]() $\mathbb {S}$
be the set of spherical objects of
$\mathbb {S}$
be the set of spherical objects of
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $\mathbb {R}^{\mathbb {S}}$
be the space of real-valued functions on
$\mathbb {R}^{\mathbb {S}}$
be the space of real-valued functions on
![]() $\mathbb {S}$
. Let
$\mathbb {S}$
. Let
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
denote the projectivisation of this space; that is,
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
denote the projectivisation of this space; that is,
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R}) = (\mathbb {R}^{\mathbb {S}} \setminus 0)/\mathbb {R}^{\times }$
. Recall the definition of the q-mass of an object X, given a stability condition
$\mathbb {P}^{\mathbb {S}}(\mathbb {R}) = (\mathbb {R}^{\mathbb {S}} \setminus 0)/\mathbb {R}^{\times }$
. Recall the definition of the q-mass of an object X, given a stability condition
![]() ${\tau }$
, denoted
${\tau }$
, denoted
![]() $m_{q,{\tau }}(X)$
(Definition 3.3). For any
$m_{q,{\tau }}(X)$
(Definition 3.3). For any
![]() $q> 0$
, we have a map
$q> 0$
, we have a map
defined as
The following proposition states that a stability condition can be recovered uniquely up to
![]() $\mathbb {C}$
-action from its q-mass vector.
$\mathbb {C}$
-action from its q-mass vector.
Proposition 5.1 (Injectivity).
Let
![]() $\mathcal T$
be the 2-CY category associated to a connected quiver. Let
$\mathcal T$
be the 2-CY category associated to a connected quiver. Let
![]() $\mathbb {S}$
be the set of spherical objects of
$\mathbb {S}$
be the set of spherical objects of
![]() $\mathcal T$
. Then, the map
$\mathcal T$
. Then, the map
![]() $m_q \colon \operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C} \to \mathbb {P}^{\mathbb {S}}(\mathbb {R}) $
is injective.
$m_q \colon \operatorname {\mathrm {Stab}}(\mathcal T)/\mathbb {C} \to \mathbb {P}^{\mathbb {S}}(\mathbb {R}) $
is injective.
Injectivity in the case that
![]() $q = 1$
is proven in [Reference Bapat, Deopurkar and Licata2, Proposition 4.1]. This proof works in general, given q-deformed versions of two trigonometric relations: Ikeda’s ‘q-deformed triangle inequality’ [Reference Ikeda8, Lemma 3.6] and a ‘q-deformed SSS-triangle congruence theorem’, which we describe presently.
$q = 1$
is proven in [Reference Bapat, Deopurkar and Licata2, Proposition 4.1]. This proof works in general, given q-deformed versions of two trigonometric relations: Ikeda’s ‘q-deformed triangle inequality’ [Reference Ikeda8, Lemma 3.6] and a ‘q-deformed SSS-triangle congruence theorem’, which we describe presently.
For any point
![]() $z \in \mathbb {H}\cup \mathbb {R}^{>0}$
, let
$z \in \mathbb {H}\cup \mathbb {R}^{>0}$
, let
![]() $\phi (z)$
denote the phase of z. For any pair of points
$\phi (z)$
denote the phase of z. For any pair of points
![]() $z_{1}, z_{2} \in \mathbb {H}\cup \mathbb {R}^{>0}$
, say that the triangle associated to
$z_{1}, z_{2} \in \mathbb {H}\cup \mathbb {R}^{>0}$
, say that the triangle associated to
![]() $(z_{1},z_{2})$
is the Euclidean planar triangle with vertices
$(z_{1},z_{2})$
is the Euclidean planar triangle with vertices
![]() $(0, z_{1}, z_{1}+z_{2})$
. Classically, the lengths of the sides of the trangle associated to
$(0, z_{1}, z_{1}+z_{2})$
. Classically, the lengths of the sides of the trangle associated to
![]() $(z_{1},z_{2})$
would be
$(z_{1},z_{2})$
would be
![]() ${\vert } z_{1}{\vert }$
,
${\vert } z_{1}{\vert }$
,
![]() ${\vert } z_{2} {\vert }$
and
${\vert } z_{2} {\vert }$
and
![]() ${\vert } z_{1}+z_{2}{\vert }$
. For our purposes, however, it is natural to ‘q-deform’ this measure. The q-deformed length of a side of this triangle will involve both the classical length and the phase of the corresponding vector. Precisely, for
${\vert } z_{1}+z_{2}{\vert }$
. For our purposes, however, it is natural to ‘q-deform’ this measure. The q-deformed length of a side of this triangle will involve both the classical length and the phase of the corresponding vector. Precisely, for
![]() $v\in \{z_{1},z_{2},z_{1}+z_{2}\}$
, the q-deformed length of the side with classical length
$v\in \{z_{1},z_{2},z_{1}+z_{2}\}$
, the q-deformed length of the side with classical length
![]() ${\vert } v{\vert }$
is
${\vert } v{\vert }$
is
![]() $q^{\phi (v)}{\vert } v{\vert }$
. Ikeda’s q-deformed triangle inequality ([Reference Ikeda8, Lemma 3.6]) says that the q-deformed side-length satisfies the triangle inequality:
$q^{\phi (v)}{\vert } v{\vert }$
. Ikeda’s q-deformed triangle inequality ([Reference Ikeda8, Lemma 3.6]) says that the q-deformed side-length satisfies the triangle inequality:
The next lemma says that the classical SSS-property is also preserved under q-deformation: the q-deformed side-lengths uniquely determine the triangle (up to congruence).
Lemma 5.2 (q-SSS).
Let
![]() $z_{1}, z_{2}, z_{1}', z_{2}' \in \mathbb {H} \cup \mathbb {R}^{>0}$
and suppose that
$z_{1}, z_{2}, z_{1}', z_{2}' \in \mathbb {H} \cup \mathbb {R}^{>0}$
and suppose that
 $$ \begin{align*} q^{\phi(z_{1})}{\vert} z_{1} {\vert}&=q^{\phi(z_{1}')}{\vert} z_{1}' {\vert},\\ q^{\phi(z_{2})}{\vert} z_{2} {\vert}&=q^{\phi(z_{2}')}{\vert} z_{2}' {\vert},\\ q^{\phi(z_{1}+z_{2})}{\vert} z_{1} + z_{2} {\vert}&=q^{\phi(z_{1}'+z_{2}')}{\vert} z_{1}' + z_{2}' {\vert}. \end{align*} $$
$$ \begin{align*} q^{\phi(z_{1})}{\vert} z_{1} {\vert}&=q^{\phi(z_{1}')}{\vert} z_{1}' {\vert},\\ q^{\phi(z_{2})}{\vert} z_{2} {\vert}&=q^{\phi(z_{2}')}{\vert} z_{2}' {\vert},\\ q^{\phi(z_{1}+z_{2})}{\vert} z_{1} + z_{2} {\vert}&=q^{\phi(z_{1}'+z_{2}')}{\vert} z_{1}' + z_{2}' {\vert}. \end{align*} $$
Then, the triangle associated to
![]() $(z_{1}, z_{2})$
is congruent to the triangle associated to
$(z_{1}, z_{2})$
is congruent to the triangle associated to
![]() $(z_{1}', z_{2}')$
.
$(z_{1}', z_{2}')$
.
Proof. Assume that
![]() $z_{1}=z_{1}'=1$
(by rotating and scaling appropriately). For convenience, let
$z_{1}=z_{1}'=1$
(by rotating and scaling appropriately). For convenience, let
To prove the proposition, it is enough to show that given the assumption, the vector
![]() $z_{2}$
is uniquely determined by the values
$z_{2}$
is uniquely determined by the values
![]() $q^{\phi _{2}}m_{2}$
and
$q^{\phi _{2}}m_{2}$
and
![]() $q^{\phi _{12}}m_{12}$
. For any
$q^{\phi _{12}}m_{12}$
. For any
![]() $t \in [0,1]$
, let
$t \in [0,1]$
, let
![]() $w_{t}$
be the vector with phase t and length
$w_{t}$
be the vector with phase t and length
![]() $q^{-t}c$
. We explicitly construct a function
$q^{-t}c$
. We explicitly construct a function
![]() $T_{q,c}:[0,1] \to \mathbb {R}$
, which maps
$T_{q,c}:[0,1] \to \mathbb {R}$
, which maps
![]() $t \in [0,1]$
to
$t \in [0,1]$
to
![]() $q^{\phi (1+w_{t})}{\vert } 1+w_{t} {\vert }$
. If
$q^{\phi (1+w_{t})}{\vert } 1+w_{t} {\vert }$
. If
![]() $T_{q,c}$
is injective, then since
$T_{q,c}$
is injective, then since
![]() $T_{q,c}(\phi _{2})=q^{\phi _{12}}m_{12}$
, we can derive
$T_{q,c}(\phi _{2})=q^{\phi _{12}}m_{12}$
, we can derive
![]() $\phi _{2}$
from
$\phi _{2}$
from
![]() $q^{\phi _{12}}m_{12}$
. Thus, given
$q^{\phi _{12}}m_{12}$
. Thus, given
![]() $q^{\phi _{12}}m_{12}$
and
$q^{\phi _{12}}m_{12}$
and
![]() $q^{\phi _{2}}m_{2}$
, we can derive
$q^{\phi _{2}}m_{2}$
, we can derive
![]() $\phi _{2}$
and
$\phi _{2}$
and
![]() $m_{2}$
, which determine
$m_{2}$
, which determine
![]() $z_{2}$
.
$z_{2}$
.
By the law of cosines,
 $$ \begin{align*}\phi(1+w_{t}) =\frac{1}{\pi}\cos^{-1}\Big(\frac{1+c q^{-t} \cos (\pi t)}{\sqrt{1+(c q^{-t})^{2}+2 cq^{-t} \cos(\pi t)}}\Big),\end{align*} $$
$$ \begin{align*}\phi(1+w_{t}) =\frac{1}{\pi}\cos^{-1}\Big(\frac{1+c q^{-t} \cos (\pi t)}{\sqrt{1+(c q^{-t})^{2}+2 cq^{-t} \cos(\pi t)}}\Big),\end{align*} $$
and
Thus,
The derivative of
![]() $T_{q,c}$
on the interval
$T_{q,c}$
on the interval
![]() $[0,1]$
simplifies to
$[0,1]$
simplifies to
 $$ \begin{align*}T_{q,c}'(t)=-\frac{q^{f(t)}}{\pi \sqrt{c^{2}+q^{2t}+2c q^{t} \cos(\pi t)}}(cq^{t} \ln^{2}(q)\sin(\pi t)+ \pi^{2}c q^{t} \sin(\pi t)),\end{align*} $$
$$ \begin{align*}T_{q,c}'(t)=-\frac{q^{f(t)}}{\pi \sqrt{c^{2}+q^{2t}+2c q^{t} \cos(\pi t)}}(cq^{t} \ln^{2}(q)\sin(\pi t)+ \pi^{2}c q^{t} \sin(\pi t)),\end{align*} $$
where
 $$ \begin{align*}f(t)=-t+\frac{\cos^{-1}\Big(\frac{1+c q^{t}\cos(\pi t)}{\sqrt{1+(cq^{-t})^{2}+2cq^{-t} \cos(\pi t)}}\Big)}{\pi}.\end{align*} $$
$$ \begin{align*}f(t)=-t+\frac{\cos^{-1}\Big(\frac{1+c q^{t}\cos(\pi t)}{\sqrt{1+(cq^{-t})^{2}+2cq^{-t} \cos(\pi t)}}\Big)}{\pi}.\end{align*} $$
Since
![]() $T^{\prime }_{q,c}$
is evidently negative,
$T^{\prime }_{q,c}$
is evidently negative,
![]() $T_{q,c}$
is injective on
$T_{q,c}$
is injective on
![]() $[0,1]$
, completing the proof.
$[0,1]$
, completing the proof.
Further, we conjecture that the mass map is a homeomorphism onto its image.
Conjecture 5.3. Let
![]() $\mathcal T$
be the 2-CY category associated to a connected quiver and let
$\mathcal T$
be the 2-CY category associated to a connected quiver and let
![]() $\mathbb {S}$
be the set of spherical objects of
$\mathbb {S}$
be the set of spherical objects of
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $m_q$
denote the mass map for a
$m_q$
denote the mass map for a
![]() $q\in (0,\infty )$
. Then,
$q\in (0,\infty )$
. Then,
-
1. The map
 $m_q$
is a homeomorphism onto its image.
$m_q$
is a homeomorphism onto its image. -
2. The closure of the image of
 $m_q$
is a compactification of
$m_q$
is a compactification of
 $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
and is a real manifold with boundary.
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
and is a real manifold with boundary. -
3. When
 $\mathcal {T}$
is a 2-CY category of type ADE, the closure of the image of
$\mathcal {T}$
is a 2-CY category of type ADE, the closure of the image of
 $m_q$
is homeomorphic to a closed Euclidean ball.
$m_q$
is homeomorphic to a closed Euclidean ball.
In the remainder of this section we prove a weaker implication of the above conjecture in type
![]() $A_{2}$
; we show that the map
$A_{2}$
; we show that the map
![]() $m_q$
is a homeomorphism onto its image, that the image of
$m_q$
is a homeomorphism onto its image, that the image of
![]() $m_q$
is homeomorphic to an open Euclidean disk and that the boundary of the closure is homeomorphic to a circle.
$m_q$
is homeomorphic to an open Euclidean disk and that the boundary of the closure is homeomorphic to a circle.
The analogue of this conjecture for the 2-CY category of the
![]() $A_{2}$
-quiver at
$A_{2}$
-quiver at
![]() $q=1$
is proved in [Reference Bapat, Deopurkar and Licata2, Proposition 5.7]. The proof of the (following) q-deformed proposition is essentially the same (again switching the triangle inequality for the q-deformed analogue from [Reference Ikeda8, Lemma 3.6]).
$q=1$
is proved in [Reference Bapat, Deopurkar and Licata2, Proposition 5.7]. The proof of the (following) q-deformed proposition is essentially the same (again switching the triangle inequality for the q-deformed analogue from [Reference Ikeda8, Lemma 3.6]).
Proposition 5.4 (Homeomorphism).
The map
![]() $m_{q}\colon \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C} \to \mathbb {P}^{\mathbb {S}}(\mathbb {R})$
is a homeomorphism onto its image. Moreover, the closure of
$m_{q}\colon \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C} \to \mathbb {P}^{\mathbb {S}}(\mathbb {R})$
is a homeomorphism onto its image. Moreover, the closure of
![]() $m_{q}(\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C})$
is compact in
$m_{q}(\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C})$
is compact in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
.
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
.
5.2 The deformed mass embedding for N-CY categories
While the results of this paper focus on the
![]() $2$
-CY case, we make a remark about the deformed mass embedding for an N-CY category associated to a connected quiver for any
$2$
-CY case, we make a remark about the deformed mass embedding for an N-CY category associated to a connected quiver for any
![]() $N> 2$
.
$N> 2$
.
The construction of these categories is analogous to the constructions discussed in [Reference Bapat, Deopurkar and Licata2, Section 2.1], where the path-length grading is modified so that the loop map has degree N. In particular, for any edge
![]() $e \colon i \to j$
in the double of the quiver, choose
$e \colon i \to j$
in the double of the quiver, choose
![]() $d_e \in \mathbb {N}$
as the degree of e with the following constraint. If
$d_e \in \mathbb {N}$
as the degree of e with the following constraint. If
![]() $\overline {e} \colon j \to i$
is the opposite edge to e, we have
$\overline {e} \colon j \to i$
is the opposite edge to e, we have
![]() $d_e + d_{\overline {e}} = N$
. Each such choice of integers
$d_e + d_{\overline {e}} = N$
. Each such choice of integers
![]() $d_e$
yields a corresponding N-CY category.
$d_e$
yields a corresponding N-CY category.
Fix
![]() $N> 2$
. Fix a corresponding N-CY category
$N> 2$
. Fix a corresponding N-CY category
![]() $\mathcal {T}$
, where
$\mathcal {T}$
, where
![]() $d_e$
is the degree of an edge e with
$d_e$
is the degree of an edge e with
![]() $d_e + d_{\overline {e}} = N$
. Let
$d_e + d_{\overline {e}} = N$
. Let
![]() $\mathbb {S}$
be the set of (N)-spherical objects of
$\mathbb {S}$
be the set of (N)-spherical objects of
![]() $\mathcal {T}$
. Exactly as for
$\mathcal {T}$
. Exactly as for
![]() $N = 2$
, we have a q-deformed mass map
$N = 2$
, we have a q-deformed mass map
Let
![]() $\mathcal {T}$
be an N-CY category associated to a connected quiver, where
$\mathcal {T}$
be an N-CY category associated to a connected quiver, where
![]() $N> 2$
. In contrast to Proposition 5.1, the mass map
$N> 2$
. In contrast to Proposition 5.1, the mass map
![]() $m_q \colon \operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
is usually not injective, as demonstrated by the following example.
$m_q \colon \operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
is usually not injective, as demonstrated by the following example.
Example 5.5. The doubled
![]() $A_2$
quiver gives a simple counterexample to injectivity of the mass map for N-CY categories with
$A_2$
quiver gives a simple counterexample to injectivity of the mass map for N-CY categories with
![]() $N> 2$
. Suppose the vertices are indexed by the numbers
$N> 2$
. Suppose the vertices are indexed by the numbers
![]() $\{1, 2\}$
. For the edge
$\{1, 2\}$
. For the edge
![]() $e \colon 1 \to 2$
, set
$e \colon 1 \to 2$
, set
![]() $d_e = 1$
. For the opposite edge
$d_e = 1$
. For the opposite edge
![]() $\overline {e} \colon 2 \to 1$
, set
$\overline {e} \colon 2 \to 1$
, set
![]() $d_{\overline {e}} = N - 1$
. Then, the only nontrivial extension E between
$d_{\overline {e}} = N - 1$
. Then, the only nontrivial extension E between
![]() $P_1$
and
$P_1$
and
![]() $P_2$
is realised by the degree
$P_2$
is realised by the degree
![]() $1$
map
$1$
map
![]() $P_1 \to P_2$
. Define a stability condition
$P_1 \to P_2$
. Define a stability condition
![]() $\tau $
whose
$\tau $
whose
![]() $[0,1)$
heart is
$[0,1)$
heart is
![]() $\heartsuit _{\operatorname {\mathrm {std}}}$
, by choosing
$\heartsuit _{\operatorname {\mathrm {std}}}$
, by choosing
![]() $Z_{\tau }(P_1)$
and
$Z_{\tau }(P_1)$
and
![]() $Z_{\tau }(P_2)$
to lie in the upper half plane, with the phase of
$Z_{\tau }(P_2)$
to lie in the upper half plane, with the phase of
![]() $P_2$
higher than the phase of
$P_2$
higher than the phase of
![]() $P_1$
, as shown in the figure below. It is easy to check that E is not semistable and, furthermore, that
$P_1$
, as shown in the figure below. It is easy to check that E is not semistable and, furthermore, that
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are the only stable objects of
$P_2$
are the only stable objects of
![]() $\heartsuit _{\operatorname {\mathrm {std}}}$
.
$\heartsuit _{\operatorname {\mathrm {std}}}$
.

Let
![]() $m_2$
and
$m_2$
and
![]() $\varphi _2$
be the modulus and phase of
$\varphi _2$
be the modulus and phase of
![]() $Z(P_2)$
, respectively, in
$Z(P_2)$
, respectively, in
![]() $\tau $
. Now consider a stability condition
$\tau $
. Now consider a stability condition
![]() $\tau '$
defined as follows. Set
$\tau '$
defined as follows. Set
![]() $Z_{\tau '}(P_1) = Z_{\tau }(P_1)$
, and change
$Z_{\tau '}(P_1) = Z_{\tau }(P_1)$
, and change
![]() $Z_{\tau '}(P_2)$
to be any other vector in the upper half plane whose phase is higher than the phase of
$Z_{\tau '}(P_2)$
to be any other vector in the upper half plane whose phase is higher than the phase of
![]() $P_1$
and which satisfies
$P_1$
and which satisfies
For example, at
![]() $q = 1$
, this is achieved simply by rotating
$q = 1$
, this is achieved simply by rotating
![]() $Z_{\tau }(P_2)$
slightly.
$Z_{\tau }(P_2)$
slightly.

It is clear that
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
define distinct points of
$\tau '$
define distinct points of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
. However, since
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
. However, since
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are the only stable objects in both
$P_2$
are the only stable objects in both
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
, we have
$\tau '$
, we have
![]() $m_q(\tau ) = m_q(\tau ')$
by construction. In particular, the mass map is not injective.
$m_q(\tau ) = m_q(\tau ')$
by construction. In particular, the mass map is not injective.
However, we can achieve injectivity by considering a product of two distinct deformed mass maps.
Proposition 5.6. Let
![]() $q,r> 0$
be two distinct real numbers. Let
$q,r> 0$
be two distinct real numbers. Let
![]() $\mathcal {T}$
be an N-CY category associated to connected quiver, where
$\mathcal {T}$
be an N-CY category associated to connected quiver, where
![]() $N \geq 2$
. The map
$N \geq 2$
. The map
is injective.
Proof. We present a sketch of the proof. We again follow the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 4.1] with modifications to the second half of the argument.
Let
![]() $\tau $
be a stability condition, which we may assume to be a standard stability condition by applying a suitable braid. This follows from, for example, [Reference Ikeda7, Proposition 4.13] as remarked in [Reference Bapat, Deopurkar and Licata2, Proposition 4.1] and is true for an N-CY category for any N. By applying a phase shift if necessary, assume that the phases of the (stable) objects
$\tau $
be a stability condition, which we may assume to be a standard stability condition by applying a suitable braid. This follows from, for example, [Reference Ikeda7, Proposition 4.13] as remarked in [Reference Bapat, Deopurkar and Licata2, Proposition 4.1] and is true for an N-CY category for any N. By applying a phase shift if necessary, assume that the phases of the (stable) objects
![]() $P_i$
all lie in the interval
$P_i$
all lie in the interval
![]() $[0,1)$
. Let
$[0,1)$
. Let
![]() $\tau '$
be another stability condition such that
$\tau '$
be another stability condition such that
![]() $(m_q \times m_r)(\tau ) = (m_q \times m_r)(\tau ')$
. The same argument as in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 4.1] shows that
$(m_q \times m_r)(\tau ) = (m_q \times m_r)(\tau ')$
. The same argument as in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 4.1] shows that
![]() $\tau '$
must have the same collection of stable objects as
$\tau '$
must have the same collection of stable objects as
![]() $\tau $
. We now show that they describe the same point in
$\tau $
. We now show that they describe the same point in
![]() $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
.
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
.
The equation
![]() $(m_q \times m_r)(\tau ) = (m_q \times m_r)(\tau ')$
shows that there is a global positive real scalar
$(m_q \times m_r)(\tau ) = (m_q \times m_r)(\tau ')$
shows that there is a global positive real scalar
![]() $\lambda $
such that for any object X in the category, we have
$\lambda $
such that for any object X in the category, we have
Explicitly, suppose
![]() $X = P_i$
for some i. Then, we have
$X = P_i$
for some i. Then, we have
 $$ \begin{align*} q^{\phi_{\tau}(P_i)}|Z_{\tau}(P_i)| &= \lambda \cdot q^{\phi_{\tau'}(P_i)}|Z_{\tau'}(P_i)|,\\ r^{\phi_{\tau}(P_i)}|Z_{\tau}(P_i)| &= \lambda \cdot r^{\phi_{\tau'}(P_i)}|Z_{\tau'}(P_i)|. \end{align*} $$
$$ \begin{align*} q^{\phi_{\tau}(P_i)}|Z_{\tau}(P_i)| &= \lambda \cdot q^{\phi_{\tau'}(P_i)}|Z_{\tau'}(P_i)|,\\ r^{\phi_{\tau}(P_i)}|Z_{\tau}(P_i)| &= \lambda \cdot r^{\phi_{\tau'}(P_i)}|Z_{\tau'}(P_i)|. \end{align*} $$
Taking the quotient of these two equations, and noting that
![]() $q \neq r$
are positive, we conclude that
$q \neq r$
are positive, we conclude that
![]() $\phi _{\tau }(P_i) = \phi _{\tau '}(P_i)$
for every i. Further, from the equations above, we conclude that
$\phi _{\tau }(P_i) = \phi _{\tau '}(P_i)$
for every i. Further, from the equations above, we conclude that
for each i. In other words, the central charges of
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
are equal up to a real scalar, which means that
$\tau '$
are equal up to a real scalar, which means that
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
are equal in
$\tau '$
are equal in
![]() $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
.
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
.
The combinatorics of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
, as well as that of the images of
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
, as well as that of the images of
![]() $m_q$
and
$m_q$
and
![]() $m_q \times m_r$
appears to be extremely interesting and worthy of investigation. In particular, it would be interesting to study how the combinatorics of
$m_q \times m_r$
appears to be extremely interesting and worthy of investigation. In particular, it would be interesting to study how the combinatorics of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
is related to the structure of the exchange graphs of the N-CY categories as discussed, for example, in [Reference King and Qiu11]. However, we do not explore these directions in this paper.
$\operatorname {\mathrm {Stab}}(\mathcal {T})/\mathbb {C}$
is related to the structure of the exchange graphs of the N-CY categories as discussed, for example, in [Reference King and Qiu11]. However, we do not explore these directions in this paper.
5.3 Analogy with the q-Farey tessellation
In the remainder of this section, we will only work with the category
![]() $\mathcal {C}_2$
and with
$\mathcal {C}_2$
and with
![]() $q \in (0,1)$
(although everything we state is true for
$q \in (0,1)$
(although everything we state is true for
![]() $q \in (1, \infty )$
up to sign/orientation). We will use
$q \in (1, \infty )$
up to sign/orientation). We will use
![]() $M_{q}$
to denote
$M_{q}$
to denote
Our goal is to classify the points in the ‘boundary’
![]() $\partial \overline {M}_{q}:=\overline {M}_{q}\setminus M_{q}$
. We will show that the
$\partial \overline {M}_{q}:=\overline {M}_{q}\setminus M_{q}$
. We will show that the
![]() $\operatorname {\mathrm {occ}}_{q}$
and
$\operatorname {\mathrm {occ}}_{q}$
and
![]() $\overline {\hom }_{q}$
functionals lie in
$\overline {\hom }_{q}$
functionals lie in
![]() $\partial \overline {M}_{q}$
and then use Theorem 4.7 and Theorem 4.8 to completely describe
$\partial \overline {M}_{q}$
and then use Theorem 4.7 and Theorem 4.8 to completely describe
![]() $\partial \overline {M}_{q}$
.
$\partial \overline {M}_{q}$
.
In Section 2.2, we described ‘q-deformed rational curves’ as limits of sequences of triangles in the q-deformed Farey tessellation. These curves satisfy two notable properties:
-
1. they are in natural,
 $B_{3}$
-equivariant bijection with the rational numbers;
$B_{3}$
-equivariant bijection with the rational numbers; -
2. their union is a dense subset of the boundary of the q-Farey tessellation.
The same phenomenon occurs in the embedding of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
in projective space. Let
$\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
in projective space. Let
![]() $\overline {\hom }_{q}(X),\operatorname {\mathrm {occ}}_{q}(X)$
denote the functionals
$\overline {\hom }_{q}(X),\operatorname {\mathrm {occ}}_{q}(X)$
denote the functionals
![]() $\overline {\hom }_{q}(X,\cdotp ), \operatorname {\mathrm {occ}}_{q}(X,\cdotp )$
, respectively, viewed as elements of
$\overline {\hom }_{q}(X,\cdotp ), \operatorname {\mathrm {occ}}_{q}(X,\cdotp )$
, respectively, viewed as elements of
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
. That is,
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
. That is,
Set
as indicated in the introduction to the paper.
We will show shortly that the convex sets
![]() $I_{q,X}$
for
$I_{q,X}$
for
![]() $X \in \mathbb {S}$
arise as limits of stability conditions. The functional
$X \in \mathbb {S}$
arise as limits of stability conditions. The functional
![]() $\overline {\hom }_{q}(X)$
should be thought of as the correspondent of the left q-deformed rational number naturally associated to X and
$\overline {\hom }_{q}(X)$
should be thought of as the correspondent of the left q-deformed rational number naturally associated to X and
![]() $\operatorname {\mathrm {occ}}_{q}(X)$
as the correspondent of the right q-deformed rational; together with their convex combinations, we obtain a perfect analogue of the q-deformed rational curve.
$\operatorname {\mathrm {occ}}_{q}(X)$
as the correspondent of the right q-deformed rational; together with their convex combinations, we obtain a perfect analogue of the q-deformed rational curve.
Recall the definition of standard stability conditions from Definition 4.1. The subset of the space of stability conditions that corresponds to the first two Farey triangles is given by the following definition:
Definition 5.7 [Reference Bapat, Deopurkar and Licata2, Section 5.3].
A standard stability condition
![]() ${\tau }$
is type-A if
${\tau }$
is type-A if
![]() $P_{21}$
is semistable with respect to
$P_{21}$
is semistable with respect to
![]() ${\tau }$
, and type-B if
${\tau }$
, and type-B if
![]() $P_{12}$
is semistable with respect to
$P_{12}$
is semistable with respect to
![]() ${\tau }$
. A type-A (resp, type-B) standard stability condition is strictly type-A (resp. strictly type-B) if it is not both type-A and type-B.
${\tau }$
. A type-A (resp, type-B) standard stability condition is strictly type-A (resp. strictly type-B) if it is not both type-A and type-B.
Let
![]() $\Lambda $
denote the set of standard stability conditions, let
$\Lambda $
denote the set of standard stability conditions, let
![]() $\Lambda _{A}$
(resp.
$\Lambda _{A}$
(resp.
![]() $\Lambda _{B}$
) denote the set of type-A (resp. type-B) standard stability conditions.
$\Lambda _{B}$
) denote the set of type-A (resp. type-B) standard stability conditions.
Think of
![]() $\Lambda _{A}$
as the Farey triangle with vertices
$\Lambda _{A}$
as the Farey triangle with vertices
![]() $0,\infty ,1$
, and
$0,\infty ,1$
, and
![]() $\Lambda _{B}$
as the Farey triangle with vertices
$\Lambda _{B}$
as the Farey triangle with vertices
![]() $0,\infty ,-1$
. So the initial edge E is the intersection
$0,\infty ,-1$
. So the initial edge E is the intersection
![]() $\Lambda _{A}\cap \Lambda _{B}$
. Its image under the q-mass map is the interval between
$\Lambda _{A}\cap \Lambda _{B}$
. Its image under the q-mass map is the interval between
![]() $\operatorname {\mathrm {occ}}_{q}(P_{1})$
and
$\operatorname {\mathrm {occ}}_{q}(P_{1})$
and
![]() $\operatorname {\mathrm {occ}}_{q}(P_{2})$
:
$\operatorname {\mathrm {occ}}_{q}(P_{2})$
:
Lemma 5.8. We have an equality:
We can now state how the ‘intervals’
![]() $I_{q,X}$
arise in
$I_{q,X}$
arise in
![]() $\partial \overline {M}_{q}$
.
$\partial \overline {M}_{q}$
.
Proposition 5.9. Consider any
![]() $X \in \mathbb {S}$
and suppose that
$X \in \mathbb {S}$
and suppose that
![]() $X={\beta } P_{1}[n]$
. Then,
$X={\beta } P_{1}[n]$
. Then,
Proof. We first prove this statement for
![]() $\beta = \operatorname {id}$
and then deduce it for all other
$\beta = \operatorname {id}$
and then deduce it for all other
![]() $\beta $
by equivariance. Thus, we have to show that
$\beta $
by equivariance. Thus, we have to show that
By Lemma 5.8,
Since
![]() $\sigma _{1}^{-1}P_{1}=P_{1}[1]$
, we have that
$\sigma _{1}^{-1}P_{1}=P_{1}[1]$
, we have that
Thus, all we need to show is that
Let
![]() $X,Y \in \mathbb {S}$
be such that
$X,Y \in \mathbb {S}$
be such that
![]() $X \geq 0$
,
$X \geq 0$
,
![]() $Y \leq 0$
. Consider the following abbreviated vector in
$Y \leq 0$
. Consider the following abbreviated vector in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
, representing
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
, representing
![]() $\sigma _{1}^{-m}\operatorname {\mathrm {occ}}_{q}(P_{1})$
$\sigma _{1}^{-m}\operatorname {\mathrm {occ}}_{q}(P_{1})$
 $$ \begin{align*} \sigma_{1}^{-m} \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, P_{1}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},Y) \end{bmatrix} &=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, \sigma_{1}^{m}P_{1}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2},\sigma_{1}^{m}P_{2})\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, \sigma_{1}^{m}X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},\sigma_{1}^{m}Y) \end{bmatrix} \\ &=\begin{bmatrix} q^{-m}\\ [m]_{q^{-1}}\\ [m-1]_{q^{-1}}(1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},Y)+(q^{-1}-1)[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \sigma_{1}^{-m} \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, P_{1}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},Y) \end{bmatrix} &=\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, \sigma_{1}^{m}P_{1}) \\ \operatorname{\mathrm{occ}}_{q}(P_{2},\sigma_{1}^{m}P_{2})\\ \operatorname{\mathrm{occ}}_{q}(P_{2}, \sigma_{1}^{m}X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},\sigma_{1}^{m}Y) \end{bmatrix} \\ &=\begin{bmatrix} q^{-m}\\ [m]_{q^{-1}}\\ [m-1]_{q^{-1}}(1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ \operatorname{\mathrm{occ}}_{q}(P_{2},Y)+(q^{-1}-1)[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+[m]_{q^{-1}}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
We multiply all the coordinates by
![]() $\frac {q^{-1}}{[m]_{q^{-1}}}$
to obtain:
$\frac {q^{-1}}{[m]_{q^{-1}}}$
to obtain:
 $$ \begin{align*} \begin{bmatrix} \frac{q^{-m-1}}{[m]_{q^{-1}}}\\ q^{-1}\\ \frac{[m-1]_{q^{-1}}}{[m]_{q^{-1}}}(q^{-1}-q^{-2})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ \frac{q^{-1}}{[m]_{q^{-1}}}\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+(q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \begin{bmatrix} \frac{q^{-m-1}}{[m]_{q^{-1}}}\\ q^{-1}\\ \frac{[m-1]_{q^{-1}}}{[m]_{q^{-1}}}(q^{-1}-q^{-2})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ \frac{q^{-1}}{[m]_{q^{-1}}}\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+(q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
When we send m to infinity, we get:
 $$ \begin{align*} \begin{bmatrix} q^{-2}-q^{-1}\\ q^{-1}\\ (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \begin{bmatrix} q^{-2}-q^{-1}\\ q^{-1}\\ (1-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},X)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},X)\\ (q^{-2}-q^{-1})\operatorname{\mathrm{occ}}_{q}(P_{2},Y)+q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{1},Y) \end{bmatrix}. \end{align*} $$
Comparing to the
![]() $\hom $
-values lemma (Lemma 4.13), we see that this is indeed equal to
$\hom $
-values lemma (Lemma 4.13), we see that this is indeed equal to
![]() $\overline {\hom }_{q}(P_{1})$
.
$\overline {\hom }_{q}(P_{1})$
.
We will check that the appearance of these functionals really is a nontrivial result of taking the closure.
Lemma 5.10 (Disjointness 1).
For any
![]() $X \in \mathbb {S}$
and all
$X \in \mathbb {S}$
and all
![]() $t \in [0,1]$
,
$t \in [0,1]$
,
To prove this lemma, we need to give a more thorough account of the dynamics of the q-deformed triangle inequality. Consider any stability condition
![]() ${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. By the triangle inequality for the q-deformed mass [Reference Ikeda8, Proposition 3.3], we have the inequalities
${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. By the triangle inequality for the q-deformed mass [Reference Ikeda8, Proposition 3.3], we have the inequalities
The next lemma describes when these inequalities degenerate into equalities; it is the q-analogue of the phenomenon noted at [Reference Bapat, Deopurkar and Licata2, Remark 5.15].
Lemma 5.11 (q-Degeneracy).
Consider any stability condition
![]() ${\tau }$
. If
${\tau }$
. If
![]() ${\tau }$
is strictly type-A standard, then the triangle inequalities (5.1), (5.2), (5.3) are strict inequalities. If
${\tau }$
is strictly type-A standard, then the triangle inequalities (5.1), (5.2), (5.3) are strict inequalities. If
![]() ${\tau }$
is not strictly standard, then one of the triangle inequalities (5.1), (5.2), (5.3) is an equality.
${\tau }$
is not strictly standard, then one of the triangle inequalities (5.1), (5.2), (5.3) is an equality.
Interchanging the indices 1 and 2 gives corresponding inequalities for type-B stability conditions for which Lemma 5.11 holds.
Now we are ready to prove the disjointness of
![]() $I_{q,X}$
and
$I_{q,X}$
and
![]() $M_{q}$
.
$M_{q}$
.
Proof of Lemma 5.10.
Consider any
![]() $X \in \mathbb {S}$
. That
$X \in \mathbb {S}$
. That
![]() $\operatorname {\mathrm {occ}}_{q}(X) \notin M_{q}$
follows immediately from the fact that
$\operatorname {\mathrm {occ}}_{q}(X) \notin M_{q}$
follows immediately from the fact that
![]() $\operatorname {\mathrm {occ}}_{q}(X,X)=0$
, but
$\operatorname {\mathrm {occ}}_{q}(X,X)=0$
, but
![]() $m_{q,{\tau }}(X)>0$
for all
$m_{q,{\tau }}(X)>0$
for all
![]() ${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. Nevertheless, in order to obtain disjointness for all the convex combinations, we must give a more involved proof for both
${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. Nevertheless, in order to obtain disjointness for all the convex combinations, we must give a more involved proof for both
![]() $\operatorname {\mathrm {occ}}_{q}(X)$
and
$\operatorname {\mathrm {occ}}_{q}(X)$
and
![]() $\overline {\hom }_{q}(X)$
.
$\overline {\hom }_{q}(X)$
.
We begin with
![]() $\operatorname {\mathrm {occ}}_{q}(X)$
. Suppose to generate a contradiction that
$\operatorname {\mathrm {occ}}_{q}(X)$
. Suppose to generate a contradiction that
![]() $\operatorname {\mathrm {occ}}_{q}(X) \in M_{q}$
. Since every stability condition is in the braid group orbit of
$\operatorname {\mathrm {occ}}_{q}(X) \in M_{q}$
. Since every stability condition is in the braid group orbit of
![]() $\Lambda $
, we can assume that
$\Lambda $
, we can assume that
for some
![]() ${\tau } \in \Lambda $
. Let
${\tau } \in \Lambda $
. Let
![]() $X = {\beta } P_{1}$
for some braid
$X = {\beta } P_{1}$
for some braid
![]() ${\beta } \in B_{3}$
which can be written in strict continued form. Assume for convenience that
${\beta } \in B_{3}$
which can be written in strict continued form. Assume for convenience that
![]() ${\beta }$
has form (4.1) in the notation of Lemma 4.9, and therefore,
${\beta }$
has form (4.1) in the notation of Lemma 4.9, and therefore,
![]() ${\beta }^{-1}\sigma _{1}$
has strict continued form (4.2). That is,
${\beta }^{-1}\sigma _{1}$
has strict continued form (4.2). That is,
By Proposition 4.11, we have
 $$ \begin{align*} \overline{{\beta}^{-1}\sigma_{1}}&= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}[-1]) &-q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1}P_{12})\\ -q \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}[-1]) &\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1}P_{12}) \end{bmatrix} \\ &= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) &-q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1}P_{2})\\ -q \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) &\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1}P_{2}) \end{bmatrix} \begin{bmatrix} q^{-1} & -q^{-1} \\ 0 & 1 \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \overline{{\beta}^{-1}\sigma_{1}}&= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}[-1]) &-q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1}P_{12})\\ -q \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}[-1]) &\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1}P_{12}) \end{bmatrix} \\ &= \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1} P_{1}) &-q^{-1}\operatorname{\mathrm{occ}}_{q}(P_{2}, {\beta}^{-1}P_{2})\\ -q \operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1} P_{1}) &\operatorname{\mathrm{occ}}_{q}(P_{1}, {\beta}^{-1}P_{2}) \end{bmatrix} \begin{bmatrix} q^{-1} & -q^{-1} \\ 0 & 1 \end{bmatrix}. \end{align*} $$
Strictly speaking, the equalities hold only up to scaling by
![]() $-1$
and q. By the proof of Proposition 4.11, however, both matrices are scaled by the same factor, namely
$-1$
and q. By the proof of Proposition 4.11, however, both matrices are scaled by the same factor, namely
![]() $(-q)^{-N}$
, where N is the exponent of
$(-q)^{-N}$
, where N is the exponent of
![]() $\omega $
in Eq. (5.4). Since we only need the second equality, we can safely ignore this factor.
$\omega $
in Eq. (5.4). Since we only need the second equality, we can safely ignore this factor.
Therefore, for
![]() $i \in \{1,2\}$
,
$i \in \{1,2\}$
,
Now consider the two cases
![]() $M=0$
and
$M=0$
and
![]() $M>0$
, where M is the exponent of
$M>0$
, where M is the exponent of
![]() $\sigma _{1}$
in Eq. (5.4). If
$\sigma _{1}$
in Eq. (5.4). If
![]() $M>0$
, then
$M>0$
, then
![]() ${\beta }^{-1} \sigma _{1}^{-1}$
has form (4.2), and a similar matrix calculation gives
${\beta }^{-1} \sigma _{1}^{-1}$
has form (4.2), and a similar matrix calculation gives
If
![]() $M=0$
, then
$M=0$
, then
![]() ${\beta }^{-1} \sigma _{2}$
has form (4.2), and another similar matrix calculation gives
${\beta }^{-1} \sigma _{2}$
has form (4.2), and another similar matrix calculation gives
Assume
![]() $i=1$
(the statements for
$i=1$
(the statements for
![]() $i=2$
are needed when we prove the statement for
$i=2$
are needed when we prove the statement for
![]() $\overline {\hom }_{q}$
below). Then, Eqs. (5.5) to (5.7), along with our assumption that
$\overline {\hom }_{q}$
below). Then, Eqs. (5.5) to (5.7), along with our assumption that
![]() $m_{q}({\tau })=\operatorname {\mathrm {occ}}_{q}(X)$
, imply that:
$m_{q}({\tau })=\operatorname {\mathrm {occ}}_{q}(X)$
, imply that:
and either
or
Thus, the degeneracy lemma (Lemma 5.11) implies that
![]() ${\tau }$
is neither strictly type-A nor strictly type-B. Since we assumed that
${\tau }$
is neither strictly type-A nor strictly type-B. Since we assumed that
![]() ${\tau }$
is standard, this implies that
${\tau }$
is standard, this implies that
![]() ${\tau }$
is both type-A and type-B. However, any stability condition which is both type-A and type-B satisfies
${\tau }$
is both type-A and type-B. However, any stability condition which is both type-A and type-B satisfies
If we were to combine Eq. (5.11) with either Eq. (5.9) or Eq. (5.10), we would get that
![]() $m_{q,{\tau }}(P_{i})=0$
for either
$m_{q,{\tau }}(P_{i})=0$
for either
![]() $i = 1$
or
$i = 1$
or
![]() $i=2$
, giving the desired contradiction (as the q-mass associated to any stability condition is strictly positive on all complexes). A contradiction can be generated in the cases that
$i=2$
, giving the desired contradiction (as the q-mass associated to any stability condition is strictly positive on all complexes). A contradiction can be generated in the cases that
![]() ${\beta }$
has the form (4.2), (4.3), (4.4) in the same way. This shows that
${\beta }$
has the form (4.2), (4.3), (4.4) in the same way. This shows that
![]() $\operatorname {\mathrm {occ}}_{q}(X) \notin M_{q}$
.
$\operatorname {\mathrm {occ}}_{q}(X) \notin M_{q}$
.
Now we consider
![]() $\overline {\hom }_{q}(X)$
. Suppose to generate a contradiction that
$\overline {\hom }_{q}(X)$
. Suppose to generate a contradiction that
![]() $ \overline {\hom }_{q}(X) \in M_{q}$
. Since every stability condition is in the braid group orbit of
$ \overline {\hom }_{q}(X) \in M_{q}$
. Since every stability condition is in the braid group orbit of
![]() $\Lambda $
, we can assume that
$\Lambda $
, we can assume that
for some
![]() ${\tau }' \in \Lambda $
.
${\tau }' \in \Lambda $
.
By our computation of
![]() $\overline {\hom }_{q}$
in terms of
$\overline {\hom }_{q}$
in terms of
![]() $\operatorname {\mathrm {occ}}_{q}$
(Lemma 4.13), for
$\operatorname {\mathrm {occ}}_{q}$
(Lemma 4.13), for
![]() $j \in \{1,2,12,21\}$
, we have
$j \in \{1,2,12,21\}$
, we have
If we combine Eq. (5.12) with Eqs. (5.5) to (5.7), we re-derive Eqs. (5.8) to (5.10), replacing
![]() ${\tau }$
with
${\tau }$
with
![]() ${\tau }'$
. This delivers the same contradiction as in the case of
${\tau }'$
. This delivers the same contradiction as in the case of
![]() ${\tau }$
, proving that
${\tau }$
, proving that
![]() $\overline {\hom }_{q}(X) \notin M_{q}$
.
$\overline {\hom }_{q}(X) \notin M_{q}$
.
The proof for the rest of
![]() $I_{q,X}$
follows from the argument above. The contradiction we obtained from the degenerating inequalities carries through when we pass to convex combinations.
$I_{q,X}$
follows from the argument above. The contradiction we obtained from the degenerating inequalities carries through when we pass to convex combinations.
5.4 Embedding the boundary of
 $\overline {M_q}$
into
$\overline {M_q}$
into
 $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
We will now use Theorems 4.7 and 4.8 (the Rouquier–Zimmermann Theorems) to define a homeomorphism (essentially a projection map) from the sets
![]() $I_{q,X} = [\overline {\hom }_{q}(X),\operatorname {\mathrm {occ}}_{q}(X)] $
, lying in
$I_{q,X} = [\overline {\hom }_{q}(X),\operatorname {\mathrm {occ}}_{q}(X)] $
, lying in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
, onto the corresponding q-deformed curves from Section 2.5.
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
, onto the corresponding q-deformed curves from Section 2.5.
Let
![]() $\mathbb {O}_{q}$
denote the set
$\mathbb {O}_{q}$
denote the set
Recall that
![]() $\mathbb {Q}_{q}$
denotes the union of all the q-deformed rational curves, together with their endpoints. Fix a homeomorphism from the interval
$\mathbb {Q}_{q}$
denotes the union of all the q-deformed rational curves, together with their endpoints. Fix a homeomorphism from the interval
![]() $I_{q,P_{1}} = [\overline {\hom }_q(P_1), \operatorname {\mathrm {occ}}_q(P_1)]$
to the complete geodesic between
$I_{q,P_{1}} = [\overline {\hom }_q(P_1), \operatorname {\mathrm {occ}}_q(P_1)]$
to the complete geodesic between
![]() $1/(1-q)$
and
$1/(1-q)$
and
![]() $\infty $
, together with its endpoints. Uniquely extend this by the
$\infty $
, together with its endpoints. Uniquely extend this by the
![]() $B_3$
action to a
$B_3$
action to a
![]() $B_{3}$
-equivariant map
$B_{3}$
-equivariant map
so that
![]() $\rho _{q}$
maps
$\rho _{q}$
maps
![]() $\overline {\hom }_{q}(X)$
and
$\overline {\hom }_{q}(X)$
and
![]() $\operatorname {\mathrm {occ}}_{q}(X)$
onto
$\operatorname {\mathrm {occ}}_{q}(X)$
onto
![]() $[r/s]_{q}^{\flat }$
and
$[r/s]_{q}^{\flat }$
and
![]() $[r/s]_{q}^{\sharp }$
, respectively, where
$[r/s]_{q}^{\sharp }$
, respectively, where
![]() $r/s$
is the rational number corresponding to X. In particular, this implies that
$r/s$
is the rational number corresponding to X. In particular, this implies that
![]() $\rho _{q}$
is a bijection.
$\rho _{q}$
is a bijection.
The closure of
![]() $\mathbb {O}_q$
is contained in
$\mathbb {O}_q$
is contained in
![]() $\overline {M}_{q}$
, so we need to incorporate limits of points in
$\overline {M}_{q}$
, so we need to incorporate limits of points in
![]() $\mathbb {O}_{q}$
into our classification of
$\mathbb {O}_{q}$
into our classification of
![]() $\overline {M}_{q}$
. Let
$\overline {M}_{q}$
. Let
![]() $\overline {\mathbb {O}}_{q}$
denote the union
$\overline {\mathbb {O}}_{q}$
denote the union
As the notation suggests,
![]() $\overline {\mathbb {O}}_{q}$
is, in fact, the closure of
$\overline {\mathbb {O}}_{q}$
is, in fact, the closure of
![]() $\mathbb {O}_{q}$
(see Lemma 5.13 below). We now extend
$\mathbb {O}_{q}$
(see Lemma 5.13 below). We now extend
![]() $\rho _{q}$
to a
$\rho _{q}$
to a
![]() $B_{3}$
-equivariant homeomorphism between
$B_{3}$
-equivariant homeomorphism between
![]() $\overline {\mathbb {O}}_{q}$
and
$\overline {\mathbb {O}}_{q}$
and
![]() $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
using the following lemma.
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
using the following lemma.
Lemma 5.12. A sequence
![]() $(\operatorname {\mathrm {occ}}_{q}(X_{n}))_{n \in \mathbb {N}}$
converges in
$(\operatorname {\mathrm {occ}}_{q}(X_{n}))_{n \in \mathbb {N}}$
converges in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
if and only if
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
if and only if
![]() $(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
converges in
$(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
converges in
![]() $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. Two sequences
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. Two sequences
![]() $(\operatorname {\mathrm {occ}}_{q}(X_{n}))_{n \in \mathbb {N}}$
and
$(\operatorname {\mathrm {occ}}_{q}(X_{n}))_{n \in \mathbb {N}}$
and
![]() $(\operatorname {\mathrm {occ}}_{q}(Y_{n}))_{n \in \mathbb {N}}$
converge to the same limit if and only if
$(\operatorname {\mathrm {occ}}_{q}(Y_{n}))_{n \in \mathbb {N}}$
converge to the same limit if and only if
![]() $(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
and
$(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
and
![]() $(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(Y_{n})))_{n \in \mathbb {N}}$
converge to the same limit.
$(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(Y_{n})))_{n \in \mathbb {N}}$
converge to the same limit.
Proof. For each statement, the forwards direction is an immediate corollary of Theorem 4.7. We prove the backwards direction of the statements. Consider a sequence
![]() $(X_{n})_{n \in \mathbb {N}}$
such that
$(X_{n})_{n \in \mathbb {N}}$
such that
 $$\begin{align*}(\rho_{q}(\operatorname{\mathrm{occ}}_{q}(X_{n})))_{n \in \mathbb{N}} = \left(\frac{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})}{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})}\right)_{n \in \mathbb{N}}\end{align*}$$
$$\begin{align*}(\rho_{q}(\operatorname{\mathrm{occ}}_{q}(X_{n})))_{n \in \mathbb{N}} = \left(\frac{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})}{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})}\right)_{n \in \mathbb{N}}\end{align*}$$
converges in
![]() $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. So,
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. So,
 $$\begin{align*}\frac{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})}{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})} \xrightarrow{n \to \infty} \ell \in \mathbb{R}.\end{align*}$$
$$\begin{align*}\frac{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})}{\operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})} \xrightarrow{n \to \infty} \ell \in \mathbb{R}.\end{align*}$$
We want to show that the projective vector
converges in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
and that the limit depends only on
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
and that the limit depends only on
![]() $\lim _{n \to \infty }\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n}))$
. Our proof is inductive, exploiting the fact that
$\lim _{n \to \infty }\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n}))$
. Our proof is inductive, exploiting the fact that
![]() $B_{3}$
acts transitively on
$B_{3}$
acts transitively on
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
We know that as a sequence of projective vectors, we have
 $$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})\end{bmatrix} \xrightarrow{n \to \infty} \begin{bmatrix}\ell\\1\end{bmatrix} \in \mathbb{P}^1(\mathbb{R}).\end{align*} $$
$$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})\end{bmatrix} \xrightarrow{n \to \infty} \begin{bmatrix}\ell\\1\end{bmatrix} \in \mathbb{P}^1(\mathbb{R}).\end{align*} $$
Now consider the sequence
 $$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix}\end{align*} $$
$$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix}\end{align*} $$
in
![]() $\mathbb {P}^{1}(\mathbb {R})$
. By Proposition 4.11, we have
$\mathbb {P}^{1}(\mathbb {R})$
. By Proposition 4.11, we have
 $$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix}&= \begin{bmatrix}q^{-1}\operatorname{\mathrm{occ}}_{q}(X_{n}, P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n}, P_{1})+(-q)^{-\epsilon_{n}}\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2}) \end{bmatrix}, \end{align*} $$
$$ \begin{align*}\begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix}&= \begin{bmatrix}q^{-1}\operatorname{\mathrm{occ}}_{q}(X_{n}, P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n}, P_{1})+(-q)^{-\epsilon_{n}}\operatorname{\mathrm{occ}}_{q}(X_{n},P_{2}) \end{bmatrix}, \end{align*} $$
in
![]() $\mathbb {P}^{1}(\mathbb {R})$
, where
$\mathbb {P}^{1}(\mathbb {R})$
, where
![]() $\epsilon _{n}$
lies in
$\epsilon _{n}$
lies in
![]() $\{0,1\}$
and is equal to the sign of
$\{0,1\}$
and is equal to the sign of
![]() $X_{n}$
, as described in Definition 4.6. Since
$X_{n}$
, as described in Definition 4.6. Since
![]() $(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
converges in
$(\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n})))_{n \in \mathbb {N}}$
converges in
![]() $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
, the sign
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
, the sign
![]() $\epsilon _{n}$
is eventually a constant
$\epsilon _{n}$
is eventually a constant
![]() $\epsilon $
, which is equal to the sign of
$\epsilon $
, which is equal to the sign of
![]() $\lim _{n \to \infty }\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n}))$
.
$\lim _{n \to \infty }\rho _{q}(\operatorname {\mathrm {occ}}_{q}(X_{n}))$
.
Dividing both coordinates on the right-hand side of the equality above by
![]() $\operatorname {\mathrm {occ}}_{q}(X_{n},P_{1})$
and taking the limit as n goes to infinity, we obtain
$\operatorname {\mathrm {occ}}_{q}(X_{n},P_{1})$
and taking the limit as n goes to infinity, we obtain
 $$ \begin{align*} \begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix} & \xrightarrow{n \to \infty} \begin{bmatrix} q^{-1}\ell\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix} \end{align*} $$
$$ \begin{align*} \begin{bmatrix}\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma _{2} P_{2}) \\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1})\end{bmatrix} & \xrightarrow{n \to \infty} \begin{bmatrix} q^{-1}\ell\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix} \end{align*} $$
Thus,
 $$\begin{align*}\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} =\begin{bmatrix} q\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} \xrightarrow{n \to \infty}\begin{bmatrix} \ell\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix}. \end{align*}$$
$$\begin{align*}\begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} =\begin{bmatrix} q\operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} \xrightarrow{n \to \infty}\begin{bmatrix} \ell\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix}. \end{align*}$$
And therefore, in
![]() $\mathbb {P}^{2}(\mathbb {R})$
,
$\mathbb {P}^{2}(\mathbb {R})$
,
 $$ \begin{align*} \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} \xrightarrow{n \to \infty} \begin{bmatrix} \ell\\ 1\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \begin{bmatrix} \operatorname{\mathrm{occ}}_{q}(X_{n},P_{2})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},P_{1})\\ \operatorname{\mathrm{occ}}_{q}(X_{n},\sigma_{2}P_{1}) \end{bmatrix} \xrightarrow{n \to \infty} \begin{bmatrix} \ell\\ 1\\ 1 + (-q)^{-\epsilon}\ell \end{bmatrix}. \end{align*} $$
The rest of the proof follows inductively by transitivity of the
![]() $B_{3}$
-action on
$B_{3}$
-action on
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
Lemma 5.13. The set
![]() $\overline {\mathbb {O}}_{q}$
, as defined above, is the closure of
$\overline {\mathbb {O}}_{q}$
, as defined above, is the closure of
![]() $\mathbb {O}_{q}$
.
$\mathbb {O}_{q}$
.
Proof. Consider any sequence in
![]() $\mathbb {O}_{q}$
with the form
$\mathbb {O}_{q}$
with the form
Assuming that the sequence
![]() $(X_{n})_{n \in \mathbb {N}}$
contains infinitely many distinct elements of
$(X_{n})_{n \in \mathbb {N}}$
contains infinitely many distinct elements of
![]() $\mathbb {S}$
, using elementary properties of limits of right q-deformed rational numbers, it can be shown that
$\mathbb {S}$
, using elementary properties of limits of right q-deformed rational numbers, it can be shown that
However, by the proof of Proposition 5.9, there exists a sequence
![]() $(Y_{n})_{n \in \mathbb {N}} \in \mathbb {S}^{\mathbb {N}}$
such that
$(Y_{n})_{n \in \mathbb {N}} \in \mathbb {S}^{\mathbb {N}}$
such that
Thus,
and so by Lemma 5.12,
Thus, under the assumption that the sequence
![]() $(X_{n})_{n \in \mathbb {N}}$
contains infinitely many distinct elements of
$(X_{n})_{n \in \mathbb {N}}$
contains infinitely many distinct elements of
![]() $\mathbb {S}^{\mathbb {N}}$
, we have
$\mathbb {S}^{\mathbb {N}}$
, we have
The new points we have picked up by taking limits of
![]() $\operatorname {\mathrm {occ}}_{q}$
functionals are also nontrivial members of the closure
$\operatorname {\mathrm {occ}}_{q}$
functionals are also nontrivial members of the closure
![]() $\overline {M}_{q}$
.
$\overline {M}_{q}$
.
Lemma 5.14 (Disjointness 2).
For any
![]() $p \in \overline {\mathbb {O}}_{q}$
,
$p \in \overline {\mathbb {O}}_{q}$
,
![]() $p \notin M_{q}$
.
$p \notin M_{q}$
.
Proof. Consider any
![]() $p \in \overline {\mathbb {O}}_{q} \setminus \mathbb {O}_{q}$
and suppose we generate a contradiction that
$p \in \overline {\mathbb {O}}_{q} \setminus \mathbb {O}_{q}$
and suppose we generate a contradiction that
![]() $p=m_{q}({\tau })$
for some
$p=m_{q}({\tau })$
for some
![]() ${\tau } \in \Lambda $
. There exists a sequence
${\tau } \in \Lambda $
. There exists a sequence
![]() $(X_{k})_{k \in \mathbb {N}} \in \mathbb {S}^{\mathbb {N}}$
such that
$(X_{k})_{k \in \mathbb {N}} \in \mathbb {S}^{\mathbb {N}}$
such that
Let
![]() $X_{k}={\beta }_{k}P_{1}$
, where
$X_{k}={\beta }_{k}P_{1}$
, where
![]() ${\beta }_{k}$
is in strict continued form. Passing to a subsequence if necessary, we can assume for convenience that
${\beta }_{k}$
is in strict continued form. Passing to a subsequence if necessary, we can assume for convenience that
![]() ${\beta }_{k}$
either has form (4.1) for all
${\beta }_{k}$
either has form (4.1) for all
![]() $k \in \mathbb {N}$
or form (4.2) for all
$k \in \mathbb {N}$
or form (4.2) for all
![]() $k \in \mathbb {N}$
, in the notation of Lemma 4.9 (we can rule out the cases (4.3) and (4.4), since in these cases the limit is trivial). Let’s assume that
$k \in \mathbb {N}$
, in the notation of Lemma 4.9 (we can rule out the cases (4.3) and (4.4), since in these cases the limit is trivial). Let’s assume that
![]() ${\beta }_{k}$
has form (4.1) for all
${\beta }_{k}$
has form (4.1) for all
![]() $k \in \mathbb {N}$
. Then, by the proof of the first disjointness lemma (Lemma 5.10) we have that for all
$k \in \mathbb {N}$
. Then, by the proof of the first disjointness lemma (Lemma 5.10) we have that for all
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $i \in \{1,2\}$
,
$i \in \{1,2\}$
,
and either
or
Pass to a subsequence so that we have Eq. (5.14) for all
![]() $k \in \mathbb {N}$
or Eq. (5.15) for all
$k \in \mathbb {N}$
or Eq. (5.15) for all
![]() $k \in \mathbb {N}$
. Taking the limit, we get that
$k \in \mathbb {N}$
. Taking the limit, we get that
and either
or
As in the proof of the disjointness lemma part 1, this implies a contradiction.
5.5 Classification of the compactification of
 $\mathcal {C}_{2}$
$\mathcal {C}_{2}$
The main theorem of this section is that we have now given a full description of the closure.
Theorem 5.15. We have an equality
in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
.
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
.
We have a homeomorphism
![]() $\rho _{q}:\overline {\mathbb {O}}_{q} \to \mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. So, this theorem implies that
$\rho _{q}:\overline {\mathbb {O}}_{q} \to \mathbb {Q}_{q} \cup \mathbb {I}_{q}$
. So, this theorem implies that
![]() $\partial \overline {M}_{q}=\overline {\mathbb {O}}_{q} \cong \mathbb {R}\cup \{\infty \}$
. That is, the boundary of the q-deformed Thurston compactification of
$\partial \overline {M}_{q}=\overline {\mathbb {O}}_{q} \cong \mathbb {R}\cup \{\infty \}$
. That is, the boundary of the q-deformed Thurston compactification of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})$
is homeomorphic to a circle (see Part 3 of Proposition 2.14).
$\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})$
is homeomorphic to a circle (see Part 3 of Proposition 2.14).
Remark 5.16. We stated without proof in Proposition 2.14 that
![]() $\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
is equal to the boundary of the q-deformed Farey tesselation, so, in fact,
$\mathbb {Q}_{q} \cup \mathbb {I}_{q}$
is equal to the boundary of the q-deformed Farey tesselation, so, in fact,
![]() $\rho _{q}$
maps
$\rho _{q}$
maps
![]() $\overline {\mathbb {O}}_{q}$
onto
$\overline {\mathbb {O}}_{q}$
onto
![]() $\partial \overline {L}_{q}$
. Thus,
$\partial \overline {L}_{q}$
. Thus,
![]() $\rho _{q}$
is a
$\rho _{q}$
is a
![]() $B_{3}$
-equivariant homeomorphism from the boundary of the q-deformed compactification of
$B_{3}$
-equivariant homeomorphism from the boundary of the q-deformed compactification of
![]() $\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
onto the boundary of the q-deformed Farey tessellation.
$\operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
onto the boundary of the q-deformed Farey tessellation.
Theorem 5.15 can be bootstrapped onto the proof of the corresponding [Reference Bapat, Deopurkar and Licata2, Proposition 5.18] (which covers the case
![]() $q=1$
) using ‘q-deformed Gromov coordinates’. Consider any standard stability condition
$q=1$
) using ‘q-deformed Gromov coordinates’. Consider any standard stability condition
![]() ${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. By the triangle inequality for the q-deformed mass function [Reference Ikeda8, Proposition 3.3], there exist
${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. By the triangle inequality for the q-deformed mass function [Reference Ikeda8, Proposition 3.3], there exist
![]() $a_{{\tau }},b_{{\tau }},c_{{\tau }} \in \mathbb {R}^{\geq 0}$
such that
$a_{{\tau }},b_{{\tau }},c_{{\tau }} \in \mathbb {R}^{\geq 0}$
such that
We call
![]() $(a_{{\tau }}, b_{{\tau }}, c_{{\tau }})$
the q-Gromov coordinates associated to
$(a_{{\tau }}, b_{{\tau }}, c_{{\tau }})$
the q-Gromov coordinates associated to
![]() ${\tau }$
. The following is the q-deformation of [Reference Bapat, Deopurkar and Licata2, Proposition 5.14]. The proof is essentially identical.
${\tau }$
. The following is the q-deformation of [Reference Bapat, Deopurkar and Licata2, Proposition 5.14]. The proof is essentially identical.
Proposition 5.17 (q-Linearity).
Consider any standard stability condition
![]() ${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. Then,
${\tau } \in \operatorname {\mathrm {Stab}}(\mathcal {C}_{2})/\mathbb {C}$
. Then,
Proof of Theorem 5.15.
We just need to show that
is closed in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
(since we have already shown that
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
(since we have already shown that
![]() $\overline {\mathbb {O}}_{q} \subset \partial \overline {M}_{q}$
). Consider any sequence
$\overline {\mathbb {O}}_{q} \subset \partial \overline {M}_{q}$
). Consider any sequence
![]() $(m_{q}({\tau }_{n}))_{n \in \mathbb {N}}$
which converges to a limit in
$(m_{q}({\tau }_{n}))_{n \in \mathbb {N}}$
which converges to a limit in
![]() $\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
. Let
$\mathbb {P}^{\mathbb {S}}(\mathbb {R})$
. Let
![]() ${\tau }_{n}={\beta }_{n}{\tau }_{n}^{\operatorname {\mathrm {std}}}$
, where each
${\tau }_{n}={\beta }_{n}{\tau }_{n}^{\operatorname {\mathrm {std}}}$
, where each
![]() ${\tau }_{n}^{\operatorname {\mathrm {std}}}$
is a standard stability condition.
${\tau }_{n}^{\operatorname {\mathrm {std}}}$
is a standard stability condition.
Suppose
![]() $\{{\beta }_{n}\mid n \in \mathbb {N}\}$
is a finite set. The proof that
$\{{\beta }_{n}\mid n \in \mathbb {N}\}$
is a finite set. The proof that
![]() $\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in
$\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in
![]() $M_{q} \cup \overline {\mathbb {O}}_{q}$
is easy and identical to that in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.18]. Briefly,
$M_{q} \cup \overline {\mathbb {O}}_{q}$
is easy and identical to that in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.18]. Briefly,
![]() $\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in the union of
$\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in the union of
![]() ${\beta }_{n}(\overline {\Lambda })$
for finitely many
${\beta }_{n}(\overline {\Lambda })$
for finitely many
![]() ${\beta }_{n}$
, and each of these sets lies in
${\beta }_{n}$
, and each of these sets lies in
![]() $M_{q} \cup \overline {\mathbb {O}}_{q}$
by [Reference Bapat, Deopurkar and Licata2, Proposition 5.16].
$M_{q} \cup \overline {\mathbb {O}}_{q}$
by [Reference Bapat, Deopurkar and Licata2, Proposition 5.16].
Now suppose that
![]() $\{{\beta }_{n}\mid n \in \mathbb {N}\}$
is an infinite set. Consider the two corresponding sets of sequences
$\{{\beta }_{n}\mid n \in \mathbb {N}\}$
is an infinite set. Consider the two corresponding sets of sequences
Since
![]() $\overline {\mathbb {O}}_{q}$
is sequentially compact, we can assume (simultaneously passing to subsequences if necessary) that all these sequences converge. Let us denote the limits
$\overline {\mathbb {O}}_{q}$
is sequentially compact, we can assume (simultaneously passing to subsequences if necessary) that all these sequences converge. Let us denote the limits
![]() $p_{1},p_{2},p_{21}$
and
$p_{1},p_{2},p_{21}$
and
![]() $p_{1,q}, p_{2,q}, p_{21,q}$
, respectively. It is shown that
$p_{1,q}, p_{2,q}, p_{21,q}$
, respectively. It is shown that
![]() $p_{1}=p_{2}=p_{21}$
in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.18]. The limit
$p_{1}=p_{2}=p_{21}$
in the proof of [Reference Bapat, Deopurkar and Licata2, Proposition 5.18]. The limit
![]() $p_{1}=p_{2}=p_{21}$
corresponds to a real number, namely
$p_{1}=p_{2}=p_{21}$
corresponds to a real number, namely
![]() $\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
. We split the remainder of the proof into two cases, depending on whether
$\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
. We split the remainder of the proof into two cases, depending on whether
![]() $\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is rational or irrational.
$\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is rational or irrational.
Suppose that
![]() $\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is irrational. Then, by the characterisation of limits of right q-rationals above (Theorem 2.12), we have that
$\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is irrational. Then, by the characterisation of limits of right q-rationals above (Theorem 2.12), we have that
![]() $\rho _{q}(p_{1,q})=\rho _{q}(p_{2,q})=\rho _{q}(p_{21,q})$
is the unique ‘q-irrational’ corresponding to
$\rho _{q}(p_{1,q})=\rho _{q}(p_{2,q})=\rho _{q}(p_{21,q})$
is the unique ‘q-irrational’ corresponding to
![]() $\rho _{q}(p_{1})=\rho _{q}(p_{2})=\rho _{q}(p_{21})$
. Since
$\rho _{q}(p_{1})=\rho _{q}(p_{2})=\rho _{q}(p_{21})$
. Since
![]() $\rho _{q}$
is a homeomorphism, this implies that
$\rho _{q}$
is a homeomorphism, this implies that
![]() $p_{1,q}=p_{2,q}=p_{21,q}$
.
$p_{1,q}=p_{2,q}=p_{21,q}$
.
By the q-linearity proposition (Proposition 5.17), we have sequences
![]() $(a_{n})_{n \in \mathbb {N}}$
,
$(a_{n})_{n \in \mathbb {N}}$
,
![]() $(b_{n})_{n \in \mathbb {N}}$
and
$(b_{n})_{n \in \mathbb {N}}$
and
![]() $(c_{n})_{n \in \mathbb {N}}$
in
$(c_{n})_{n \in \mathbb {N}}$
in
![]() $(\mathbb {R}^{\geq 0})^{\mathbb {N}}$
such that
$(\mathbb {R}^{\geq 0})^{\mathbb {N}}$
such that
 $$ \begin{align*} \lim_{n \to \infty} m_{q}({\tau}_{n})&=\lim_{n \to \infty} m_{q}({\beta}_{n}{\tau}_{n}^{\operatorname{\mathrm{std}}}) \\ &= \lim_{n \to \infty}\big(a_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{1})+b_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{2})+c_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{21})\big) \\&= p_{1,q}=p_{2,q}=p_{21,q}. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} m_{q}({\tau}_{n})&=\lim_{n \to \infty} m_{q}({\beta}_{n}{\tau}_{n}^{\operatorname{\mathrm{std}}}) \\ &= \lim_{n \to \infty}\big(a_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{1})+b_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{2})+c_{n}\operatorname{\mathrm{occ}}_{q}({\beta}_{n}P_{21})\big) \\&= p_{1,q}=p_{2,q}=p_{21,q}. \end{align*} $$
Since
![]() $p_{1,q}=p_{2,q}=p_{21,q} \in \overline {\mathbb {O}}_{q}$
, we have shown that the limit lies in
$p_{1,q}=p_{2,q}=p_{21,q} \in \overline {\mathbb {O}}_{q}$
, we have shown that the limit lies in
![]() $\overline {\mathbb {O}}_{q}$
.
$\overline {\mathbb {O}}_{q}$
.
Suppose that
![]() $\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is rational. By simultaneously passing to subsequences, we can assume that the image under
$\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
is rational. By simultaneously passing to subsequences, we can assume that the image under
![]() $\rho _{q}$
of each of the sequences in
$\rho _{q}$
of each of the sequences in
![]() $O_{1}$
is either an increasing sequence or a decreasing sequence. Let
$O_{1}$
is either an increasing sequence or a decreasing sequence. Let
![]() $X \in \mathbb {S}$
correspond to the rational number
$X \in \mathbb {S}$
correspond to the rational number
![]() $\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
, so by Theorem 2.12, each of
$\rho _{q=1}(p_{1})=\rho _{q=1}(p_{2})=\rho _{q=1}(p_{21})$
, so by Theorem 2.12, each of
![]() $\rho _{q}(p_{1,q}), \rho _{q}(p_{2,q}), \rho _{q}(p_{21,q})$
is either the left or right q-deformation of
$\rho _{q}(p_{1,q}), \rho _{q}(p_{2,q}), \rho _{q}(p_{21,q})$
is either the left or right q-deformation of
![]() $\rho _{q=1}(p_{1})$
. Thus, since
$\rho _{q=1}(p_{1})$
. Thus, since
![]() $\rho _{q}$
is a homeomorphism,
$\rho _{q}$
is a homeomorphism,
![]() $p_{1,q}, p_{2,q}, p_{21,q} \in \{ \operatorname {\mathrm {occ}}_{q}(X), \overline {\hom }_{q}(X)\}$
. Again, by Proposition 5.17, we have sequences
$p_{1,q}, p_{2,q}, p_{21,q} \in \{ \operatorname {\mathrm {occ}}_{q}(X), \overline {\hom }_{q}(X)\}$
. Again, by Proposition 5.17, we have sequences
![]() $(a_{n})_{n \in \mathbb {N}}, (b_{n})_{n \in \mathbb {N}}, (c_{n})_{n \in \mathbb {N}} \in (\mathbb {R}^{\geq 0})^{\mathbb {N}}$
such that
$(a_{n})_{n \in \mathbb {N}}, (b_{n})_{n \in \mathbb {N}}, (c_{n})_{n \in \mathbb {N}} \in (\mathbb {R}^{\geq 0})^{\mathbb {N}}$
such that
Since we are in projective space, we can normalise so that for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $a_{n}+b_{n}+c_{n}=1$
. Passing to subsequences if necessary, we can assume that each of
$a_{n}+b_{n}+c_{n}=1$
. Passing to subsequences if necessary, we can assume that each of
![]() $(a_{n})_{n \in \mathbb {N}}, (b_{n})_{n \in \mathbb {N}}, (c_{n})_{n\in \mathbb {N}}$
converges. Then, since
$(a_{n})_{n \in \mathbb {N}}, (b_{n})_{n \in \mathbb {N}}, (c_{n})_{n\in \mathbb {N}}$
converges. Then, since
![]() $\operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{1}), \operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{2}), \operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{21})$
converge to
$\operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{1}), \operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{2}), \operatorname {\mathrm {occ}}_{q}({\beta }_{n}P_{21})$
converge to
![]() $p_{1,q}, p_{2,q}, p_{21,q}$
, respectively, we must have that
$p_{1,q}, p_{2,q}, p_{21,q}$
, respectively, we must have that
converges to a convex combination of
![]() $p_{1,q}, p_{2,q}, p_{21,q}$
. That is, there exists
$p_{1,q}, p_{2,q}, p_{21,q}$
. That is, there exists
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
Thus, we have shown that
![]() $\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in
$\lim _{n \to \infty }m_{q}({\tau }_{n})$
lies in
![]() $[\overline {\hom }_{q}(X), \operatorname {\mathrm {occ}}_{q}(X)]$
. This completes the proof.
$[\overline {\hom }_{q}(X), \operatorname {\mathrm {occ}}_{q}(X)]$
. This completes the proof.
A Combinatorial properties of left q-deformed rational numbers
A.1 Counting ideals in quivers
We return to thinking about right q-deformed rationals and left q-deformed rationals as formal rational functions in q. The following theorem of Morier-Genoud and Ovsienko shows that the coefficients of
![]() $\mathcal {R}^{\sharp }(q)$
and
$\mathcal {R}^{\sharp }(q)$
and
![]() $\mathcal {S}^{\sharp }(q)$
have combinatorial significance.
$\mathcal {S}^{\sharp }(q)$
have combinatorial significance.
For any oriented quiver
![]() $\mathcal {G}$
, consider the poset structure given by
$\mathcal {G}$
, consider the poset structure given by
![]() $v_1 \succ v_2$
if there is an edge
$v_1 \succ v_2$
if there is an edge
![]() $v_1 \to v_2$
. We call a subquiver of
$v_1 \to v_2$
. We call a subquiver of
![]() $\mathcal {G}$
an ideal (also known as a closure) if it is a (lower) ideal of the corresponding poset. That is, an ideal of
$\mathcal {G}$
an ideal (also known as a closure) if it is a (lower) ideal of the corresponding poset. That is, an ideal of
![]() $\mathcal {G}$
is a subquiver
$\mathcal {G}$
is a subquiver
![]() ${\mathcal {H}}$
such that there do not exist edges in
${\mathcal {H}}$
such that there do not exist edges in
![]() $\mathcal {G}$
from vertices in
$\mathcal {G}$
from vertices in
![]() ${\mathcal {H}}$
to vertices outside of
${\mathcal {H}}$
to vertices outside of
![]() ${\mathcal {H}}$
. For
${\mathcal {H}}$
. For
![]() $n \in \mathbb {N}$
, an n-ideal is an ideal of size n. For any quiver
$n \in \mathbb {N}$
, an n-ideal is an ideal of size n. For any quiver
![]() $\mathcal {G}$
, let
$\mathcal {G}$
, let
![]() $C_{n}(\mathcal {G})$
denote the number of n-ideals in
$C_{n}(\mathcal {G})$
denote the number of n-ideals in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Consider any rational number
![]() $r/s \in (1, \infty )$
with continued fraction expansion
$r/s \in (1, \infty )$
with continued fraction expansion
![]() $[a_{1},\ldots ,a_{2n}]$
. Let
$[a_{1},\ldots ,a_{2n}]$
. Let
![]() $\mathcal {G}_{r/s}^{\sharp }$
denote the following quiver.
$\mathcal {G}_{r/s}^{\sharp }$
denote the following quiver.

Let
![]() $\widehat {\mathcal {G}}_{r/s}^{\sharp }$
denote the following truncated copy of
$\widehat {\mathcal {G}}_{r/s}^{\sharp }$
denote the following truncated copy of
![]() $\mathcal {G}_{r/s}$
.
$\mathcal {G}_{r/s}$
.

Theorem A.1 [Reference Morier-Genoud and Ovsienko16, Theorem 4].
Consider any rational number
![]() $r/s \in (1, \infty )$
with continued fraction expansion
$r/s \in (1, \infty )$
with continued fraction expansion
![]() $[a_{1},\ldots ,a_{n}]$
and q-deformation
$[a_{1},\ldots ,a_{n}]$
and q-deformation
 $$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\sharp}=\frac{\alpha^{\sharp}_{0}+\alpha_{1}^{\sharp}q+\cdots+\alpha_{N-1}^{\sharp}q^{N-1}+\alpha_{N}^{\sharp}q^{N}}{{\beta}_{0}^{\sharp}+{\beta}_{1}^{\sharp}q+\cdots+{\beta}_{M-1}^{\sharp}q^{M-1}+{\beta}_{M}^{\sharp}q^{M}}.\end{align*} $$
$$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\sharp}=\frac{\alpha^{\sharp}_{0}+\alpha_{1}^{\sharp}q+\cdots+\alpha_{N-1}^{\sharp}q^{N-1}+\alpha_{N}^{\sharp}q^{N}}{{\beta}_{0}^{\sharp}+{\beta}_{1}^{\sharp}q+\cdots+{\beta}_{M-1}^{\sharp}q^{M-1}+{\beta}_{M}^{\sharp}q^{M}}.\end{align*} $$
For all
![]() $i \in \mathbb {N}$
,
$i \in \mathbb {N}$
,
The following corollary (which may have independent interest) will be used later on. The left q-deformed rationals, which we motivated in Section 2 on geometric grounds and in Section 4 on homological grounds, also admit a combinatorial interpretation directly analogous to that given for the right q-deformed rationals by Theorem A.1. The left q-rational counts ideals in a slightly augmented version of
![]() $\mathcal {G}_{r/s}^{\sharp }$
. Let
$\mathcal {G}_{r/s}^{\sharp }$
. Let
![]() $\mathcal {G}^{\flat }_{r/s}$
denote the following quiver.
$\mathcal {G}^{\flat }_{r/s}$
denote the following quiver.

And let
![]() $\widehat {\mathcal {G}}^{\flat }_{r/s}$
denote the following truncation.
$\widehat {\mathcal {G}}^{\flat }_{r/s}$
denote the following truncation.

Corollary A.2. Consider any rational number
![]() $r/s \in (1, \infty )$
with left q-deformation
$r/s \in (1, \infty )$
with left q-deformation
 $$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat}=\frac{\alpha^{\flat}_{0}+\alpha^{\flat}_{1}q+\cdots+\alpha^{\flat}_{N-1}q^{N-1}+\alpha^{\flat}_{N}q^{N}}{{\beta}^{\flat}_{0}+{\beta}^{\flat}_{1}q+\cdots+{\beta}^{\flat}_{M-1}q^{M-1}+{\beta}^{\flat}_{M}q^{M}}.\end{align*} $$
$$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat}=\frac{\alpha^{\flat}_{0}+\alpha^{\flat}_{1}q+\cdots+\alpha^{\flat}_{N-1}q^{N-1}+\alpha^{\flat}_{N}q^{N}}{{\beta}^{\flat}_{0}+{\beta}^{\flat}_{1}q+\cdots+{\beta}^{\flat}_{M-1}q^{M-1}+{\beta}^{\flat}_{M}q^{M}}.\end{align*} $$
Then, for all
![]() $i \in \mathbb {N}$
,
$i \in \mathbb {N}$
,
We omit the proof, which is a straightforward application of Theorem A.1 by way of the following formula for the left q-deformed rational (using the notation of Proposition 2.11):
 $$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat} = \frac{q\mathcal{R}^{\sharp}(q)+\mathcal{R}^{\sharp\prime}(q)-q\mathcal{R}^{\sharp\prime}(q)}{q\mathcal{S}^{\sharp}(q)+\mathcal{S}^{\sharp\prime}(q)-q\mathcal{S}^{\sharp\prime}(q)}.\end{align*} $$
$$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat} = \frac{q\mathcal{R}^{\sharp}(q)+\mathcal{R}^{\sharp\prime}(q)-q\mathcal{R}^{\sharp\prime}(q)}{q\mathcal{S}^{\sharp}(q)+\mathcal{S}^{\sharp\prime}(q)-q\mathcal{S}^{\sharp\prime}(q)}.\end{align*} $$
A.2 Left q-deformed rational numbers and the Jones polynomial
The next theorem links left q-deformed rationals to the Jones polynomial of rational (two-bridge) knots. The proof of the theorem uses Theorem 4.8, although it is possible there exists a purely combinatorial proof.
Due to work by Lee and Schiffler [Reference Lee and Schiffler14, Theorem 1.2] and by Morier-Genoud and Ovsienko [Reference Morier-Genoud and Ovsienko16, Proposition A.3], the proof of this theorem is not difficult and does not involve any knot theory. For any rational number
![]() $r/s \in (1,\infty )$
, let
$r/s \in (1,\infty )$
, let
![]() $V_{r/s}(q)$
denote the Jones polynomial associated with the class of rational knots parametrised by
$V_{r/s}(q)$
denote the Jones polynomial associated with the class of rational knots parametrised by
![]() $r/s$
and let
$r/s$
and let
![]() ${\vert } V_{r/s}(q) {\vert }$
denote the polynomial obtained by making each coefficient positive.
${\vert } V_{r/s}(q) {\vert }$
denote the polynomial obtained by making each coefficient positive.
Theorem A.3. Consider any rational number
![]() $r/s \in (1, \infty )$
with left q-deformation
$r/s \in (1, \infty )$
with left q-deformation
 $$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat}=\frac{\mathcal{R}^{\flat}(q)}{\mathcal{S}^{\flat}(q)}.\end{align*} $$
$$ \begin{align*}\Big[\frac{r}{s}\Big]_{q}^{\flat}=\frac{\mathcal{R}^{\flat}(q)}{\mathcal{S}^{\flat}(q)}.\end{align*} $$
Then
![]() $\mathcal {R}^{\flat }(q)={\vert } V_{r/s}(q){\vert }$
.
$\mathcal {R}^{\flat }(q)={\vert } V_{r/s}(q){\vert }$
.
To prove this theorem, we will need the following lemma. For any rational number
![]() $r/s$
, let
$r/s$
, let
![]() ${\mathcal {H}}_{r/s}$
denote the following quiver (note that the orientation of the edges is opposite to that of
${\mathcal {H}}_{r/s}$
denote the following quiver (note that the orientation of the edges is opposite to that of
![]() $\mathcal {G}_{r/s}^{\flat }$
).
$\mathcal {G}_{r/s}^{\flat }$
).

Lemma A.4. Consider any rational number
![]() $r/s \in (1, \infty )$
. Let
$r/s \in (1, \infty )$
. Let
![]() ${\vert } V_{r/s}{\vert }=\gamma _{0}+\gamma _{1}q+\cdots +\gamma _{N-1}q^{N-1}+\gamma _{N}q^{N}$
. Then, for all
${\vert } V_{r/s}{\vert }=\gamma _{0}+\gamma _{1}q+\cdots +\gamma _{N-1}q^{N-1}+\gamma _{N}q^{N}$
. Then, for all
![]() $i \in \mathbb {N}$
,
$i \in \mathbb {N}$
,
![]() $\gamma _{i}=C_{i}({\mathcal {H}}_{r/s})$
.
$\gamma _{i}=C_{i}({\mathcal {H}}_{r/s})$
.
Lemma A.4 is an easy corollary of [Reference Morier-Genoud and Ovsienko16, Proposition A.3] since the sequence of coefficients of the normalised Jones polynomial
![]() $J_{r/s}(q)$
in their paper is just the reverse of the sequence of coefficients of the Jones polynomial
$J_{r/s}(q)$
in their paper is just the reverse of the sequence of coefficients of the Jones polynomial
![]() $V_{r/s}(q)$
, and the number of i-ideals of
$V_{r/s}(q)$
, and the number of i-ideals of
![]() ${\mathcal {H}}_{r/s}$
is equal to the number of
${\mathcal {H}}_{r/s}$
is equal to the number of
![]() $(N-i)$
-ideals of
$(N-i)$
-ideals of
![]() ${\mathcal {H}}_{r/s}$
with opposite orientation.
${\mathcal {H}}_{r/s}$
with opposite orientation.
Proof of Theorem A.3.
Let
![]() $[a_{1},\ldots ,a_{2n}]$
be the continued fraction expansion of
$[a_{1},\ldots ,a_{2n}]$
be the continued fraction expansion of
![]() $r/s$
. Let
$r/s$
. Let
![]() $\overline {\mathcal {R}}^{\flat }(q)/\overline {\mathcal {S}}^{\flat }(q)$
be the left q-deformed rational associated to
$\overline {\mathcal {R}}^{\flat }(q)/\overline {\mathcal {S}}^{\flat }(q)$
be the left q-deformed rational associated to
![]() $[a_{2n},\ldots ,a_{1}]$
. By Corollary A.2,
$[a_{2n},\ldots ,a_{1}]$
. By Corollary A.2,
![]() $\overline {\mathcal {R}}^{\flat }(q)$
counts the number of ideals in
$\overline {\mathcal {R}}^{\flat }(q)$
counts the number of ideals in
![]() ${\mathcal {H}}_{r/s}$
with its orientation reversed. It is easy to check that the number of k-ideals in an n-vertex quiver
${\mathcal {H}}_{r/s}$
with its orientation reversed. It is easy to check that the number of k-ideals in an n-vertex quiver
![]() $\mathcal {G}$
equals the number of
$\mathcal {G}$
equals the number of
![]() $(n-k)$
-ideals in
$(n-k)$
-ideals in
![]() $\mathcal {G}$
with its orientation reversed. Thus, by Lemma A.4, the sequence of coefficients of
$\mathcal {G}$
with its orientation reversed. Thus, by Lemma A.4, the sequence of coefficients of
![]() $\overline {\mathcal {R}}^{\flat }(q)$
is equal to the reverse of the sequence of coefficients of
$\overline {\mathcal {R}}^{\flat }(q)$
is equal to the reverse of the sequence of coefficients of
![]() ${\vert } V_{r/s}(q){\vert }$
. So it is sufficient to show that the sequence of coefficients of
${\vert } V_{r/s}(q){\vert }$
. So it is sufficient to show that the sequence of coefficients of
![]() $\mathcal {R}^{\flat }(q)$
is the reverse of the sequence of coefficients of
$\mathcal {R}^{\flat }(q)$
is the reverse of the sequence of coefficients of
![]() $\overline {\mathcal {R}}^{\flat }(q)$
.
$\overline {\mathcal {R}}^{\flat }(q)$
.
By Theorem 4.8, up to scaling by q, we have:
and (again up to scaling by q):
 $$ \begin{align*} \overline{\mathcal{R}}^{\flat}(q)&=\overline{\hom}_{q}(\sigma_{1}^{-a_{2n}}\sigma_{2}^{a_{2n-1}}\ldots\sigma_{1}^{-a_{2}}\sigma_{2}^{a_{1}}P_{1}, P_{2}) \\&=\overline{\hom}_{q}(P_{1}, \sigma_{2}^{-a_{1}}\sigma_{1}^{a_{2}}\ldots\sigma_{2}^{-a_{2n-1}}\sigma_{1}^{a_{2n}}P_{2}) \\ &=\overline{\hom}_{q}(P_{2}, \sigma_{1}^{-a_{1}}\sigma_{2}^{a_{2}}\ldots\sigma_{1}^{-a_{2n-1}}\sigma_{2}^{a_{2n}}P_{1}). \end{align*} $$
$$ \begin{align*} \overline{\mathcal{R}}^{\flat}(q)&=\overline{\hom}_{q}(\sigma_{1}^{-a_{2n}}\sigma_{2}^{a_{2n-1}}\ldots\sigma_{1}^{-a_{2}}\sigma_{2}^{a_{1}}P_{1}, P_{2}) \\&=\overline{\hom}_{q}(P_{1}, \sigma_{2}^{-a_{1}}\sigma_{1}^{a_{2}}\ldots\sigma_{2}^{-a_{2n-1}}\sigma_{1}^{a_{2n}}P_{2}) \\ &=\overline{\hom}_{q}(P_{2}, \sigma_{1}^{-a_{1}}\sigma_{2}^{a_{2}}\ldots\sigma_{1}^{-a_{2n-1}}\sigma_{2}^{a_{2n}}P_{1}). \end{align*} $$
Let
By the
![]() $\hom $
-values lemma (Lemma 4.13), we know that
$\hom $
-values lemma (Lemma 4.13), we know that
and an analogous result for
![]() $\overline {\hom }_{q}(\cdotp ,P_{2})$
gives that
$\overline {\hom }_{q}(\cdotp ,P_{2})$
gives that
Thus, the sequence of coefficients of
![]() $\overline {\hom }_{q}(X, P_{2})$
is the reverse of the sequence of coefficients of
$\overline {\hom }_{q}(X, P_{2})$
is the reverse of the sequence of coefficients of
![]() $\overline {\hom }_{q}(P_{2}, X)$
. Since scaling by q does not affect the sequence of coefficients, we infer that the sequence of coefficients of
$\overline {\hom }_{q}(P_{2}, X)$
. Since scaling by q does not affect the sequence of coefficients, we infer that the sequence of coefficients of
![]() $\mathcal {R}^{\flat }(q)$
is the reverse of the sequence of coefficients of
$\mathcal {R}^{\flat }(q)$
is the reverse of the sequence of coefficients of
![]() $\overline {\mathcal {R}}^{\flat }(q)$
, completing the proof.
$\overline {\mathcal {R}}^{\flat }(q)$
, completing the proof.
Acknowledgements
We thank Sophie Morier-Genoud and Valentin Ovsienko for useful comments and for pointing out several connections to related work. We are grateful to Xin Ren for a careful reading of a draft of the paper and for comments that improved the exposition. We thank the anonymous referee for their suggestions.
Funding statement
This research was supported by the Australian Research Council (FT180100069 to A.M.L.).
Competing interest
The authors have no competing interest to declare.