Article contents
DEGREE CONES AND MONOMIAL BASES OF LIE ALGEBRAS AND QUANTUM GROUPS
Published online by Cambridge University Press: 20 March 2017
Abstract
We provide ℕ-filtrations on the negative part Uq(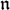 $\mathfrak{n}$−) of the quantum group associated to a finite-dimensional simple Lie algebra
$\mathfrak{n}$−) of the quantum group associated to a finite-dimensional simple Lie algebra 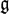 $\mathfrak{g}$, such that the associated graded algebra is a skew-polynomial algebra on
$\mathfrak{g}$, such that the associated graded algebra is a skew-polynomial algebra on 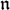 $\mathfrak{n}$−. The filtration is obtained by assigning degrees to Lusztig's quantum PBW root vectors. The possible degrees can be described as lattice points in certain polyhedral cones. In the classical limit, such a degree induces an ℕ-filtration on any finite-dimensional simple
$\mathfrak{n}$−. The filtration is obtained by assigning degrees to Lusztig's quantum PBW root vectors. The possible degrees can be described as lattice points in certain polyhedral cones. In the classical limit, such a degree induces an ℕ-filtration on any finite-dimensional simple 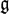 $\mathfrak{g}$-module. We prove for type An, Cn, B3, D4 and G2 that a degree can be chosen such that the associated graded modules are defined by monomial ideals, and conjecture that this is true for any
$\mathfrak{g}$-module. We prove for type An, Cn, B3, D4 and G2 that a degree can be chosen such that the associated graded modules are defined by monomial ideals, and conjecture that this is true for any 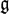 $\mathfrak{g}$.
$\mathfrak{g}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2017
References
REFERENCES
- 4
- Cited by




