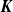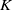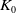1. Introduction
Unitary groups of C*-algebras have been long studied, and for many classes of operator algebras they form a complete invariant. In [Reference Dye14], Dye studied the unitary group isomorphism problem between nonatomic W*-algebras, with the assumption of weak bicontinuity of the isomorphism. He later showed that the unitary group, this time as an algebraic object, determined the type of a factor [Reference Dye15] (except for type
![]() $\text{I}_{2n}$
). He showed that such group isomorphisms were the restrictions of a *-isomorphism or a conjugate linear *-isomorphism multiplied by a possibly discontinuous character ([Reference Booth3, Appendix A] gives exposition). Sakai generalized Dye’s results to show that any uniformly continuous unitary group isomorphism between AW*-factors comes from a *-isomorphism or conjugate-linear *-isomorphism [Reference Sakai35] (see also [Reference Yen40] for general AW*-algebras which have no component of type
$\text{I}_{2n}$
). He showed that such group isomorphisms were the restrictions of a *-isomorphism or a conjugate linear *-isomorphism multiplied by a possibly discontinuous character ([Reference Booth3, Appendix A] gives exposition). Sakai generalized Dye’s results to show that any uniformly continuous unitary group isomorphism between AW*-factors comes from a *-isomorphism or conjugate-linear *-isomorphism [Reference Sakai35] (see also [Reference Yen40] for general AW*-algebras which have no component of type
![]() $I_n$
).
$I_n$
).
Dye’s method was generalized to large classes of real rank zero C*-algebras by Al-Rawashdeh, Booth and Giordano in [Reference Al-Rawashdeh, Booth and Giordano2], where they applied the method to obtain induced maps between
![]() $K$
-theory, with a general linear variant being done by Giordano and Sierakowski in [Reference Giordano and Sierakowski22]. The stably finite and purely infinite cases were handled separately. The unital, simple AH-algebras of slow dimension growth and of real rank zero were classified by the topological group isomorphism class of their unitary groups (or general linear groups), and the unital, simple, purely infinite UCT algebras were classified via the algebraic isomorphism classes of their unitary groups (or general linear groups). These results made use of the abundance of projections in real rank zero C*-algebras (at least to show there were isomorphic
$K$
-theory, with a general linear variant being done by Giordano and Sierakowski in [Reference Giordano and Sierakowski22]. The stably finite and purely infinite cases were handled separately. The unital, simple AH-algebras of slow dimension growth and of real rank zero were classified by the topological group isomorphism class of their unitary groups (or general linear groups), and the unital, simple, purely infinite UCT algebras were classified via the algebraic isomorphism classes of their unitary groups (or general linear groups). These results made use of the abundance of projections in real rank zero C*-algebras (at least to show there were isomorphic
![]() $K_0$
-groups) and made use of the Dadarlat-Elliott-Gong [Reference Dadarlat10, Reference Gong20] and Kirchberg-Phillips [Reference Phillips31] classification theorems, respectively (see Theorems 3.3.1 and 8.4.1 of [Reference Rørdam34] for each respective case).
$K_0$
-groups) and made use of the Dadarlat-Elliott-Gong [Reference Dadarlat10, Reference Gong20] and Kirchberg-Phillips [Reference Phillips31] classification theorems, respectively (see Theorems 3.3.1 and 8.4.1 of [Reference Rørdam34] for each respective case).
In [Reference Paterson28], it was proven by Paterson that two unital C*-algebras are isomorphic if and only there is an isometric isomorphism of the unitary groups, which acts as the identity on the circle. In a similar vein, the metric structure of the unitary group has also played a role in determining the Jordan *-algebra structure on C*-algebras. In [Reference Hatori and Molnár24], Hatori and Molnár showed that two unital C*-algebras are Jordan *-isomorphic if and only if their unitary groups are isometric as metric spaces, not taking into account any algebraic structure.
Chand and Robert have shown in [Reference Chand and Robert9] that if
![]() $A$
and
$A$
and
![]() $B$
are prime traceless C*-algebras with full square zero elements such that
$B$
are prime traceless C*-algebras with full square zero elements such that
![]() $U^0(A)$
, the subgroup of unitaries, which are path connected to the identity, is algebraically isomorphic to
$U^0(A)$
, the subgroup of unitaries, which are path connected to the identity, is algebraically isomorphic to
![]() $U^0(B)$
, then
$U^0(B)$
, then
![]() $A$
is either isomorphic or anti-isomorphic to
$A$
is either isomorphic or anti-isomorphic to
![]() $B$
. In fact, the group isomorphism is the restriction of a *-isomorphism or anti-*-isomorphism which follows from the fact that unitary groups associated to these C*-algebras have certain automatic continuity properties that allow one to use characterizations of commutativity preserving maps [Reference Brešar4] (see [Reference Ara and Mathieu1]). Chand and Robert also show that if
$B$
. In fact, the group isomorphism is the restriction of a *-isomorphism or anti-*-isomorphism which follows from the fact that unitary groups associated to these C*-algebras have certain automatic continuity properties that allow one to use characterizations of commutativity preserving maps [Reference Brešar4] (see [Reference Ara and Mathieu1]). Chand and Robert also show that if
![]() $A$
is a unital separable C*-algebra with at least one tracial state, then
$A$
is a unital separable C*-algebra with at least one tracial state, then
![]() $U^0(A)$
admits discontinuous automorphisms. Thus, the existence of traces is an obstruction to classification via algebraic structure on the unitary groups—at least an obstruction to unitary group homomorphisms being the restrictions of *-homomorphisms or anti-*-homomorphisms.
$U^0(A)$
admits discontinuous automorphisms. Thus, the existence of traces is an obstruction to classification via algebraic structure on the unitary groups—at least an obstruction to unitary group homomorphisms being the restrictions of *-homomorphisms or anti-*-homomorphisms.
In this paper, we show that uniformly continuous unitary group homomorphisms yield maps between traces which have several desirable
![]() $K$
-theoretic properties—especially under stricter continuity assumptions. Namely, that the homomorphism sends the circle to the circle and is contractive, which would be automatic if it had a lift to a *-homomorphism or conjugate-linear *-homomorphism.
$K$
-theoretic properties—especially under stricter continuity assumptions. Namely, that the homomorphism sends the circle to the circle and is contractive, which would be automatic if it had a lift to a *-homomorphism or conjugate-linear *-homomorphism.
We state our main results. Recall that if
![]() $A$
is a unital C*-algebra,
$A$
is a unital C*-algebra,
![]() $T(A)$
denotes the simplex of tracial states, and
$T(A)$
denotes the simplex of tracial states, and
![]() $\textrm{Aff}\, T(A)$
is the real Banach space of continuous affine functions
$\textrm{Aff}\, T(A)$
is the real Banach space of continuous affine functions
![]() $T(A) \to \mathbb{R}$
.
$T(A) \to \mathbb{R}$
.
Theorem A (Corollary 3.6). Let
![]() $A,B$
be unital C*-algebras. If
$A,B$
be unital C*-algebras. If
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a uniformly continuous group homomorphism, then there exists a bounded
$\theta \,:\, U^0(A) \to U^0(B)$
is a uniformly continuous group homomorphism, then there exists a bounded
![]() $\mathbb{R}$
-linear map
$\mathbb{R}$
-linear map
![]() $\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
such that
$\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
such that

commutes.
Here
![]() $\pi _1(\theta )$
is the map between fundamental groups induced by
$\pi _1(\theta )$
is the map between fundamental groups induced by
![]() $\theta$
, and, for a C*-algebra
$\theta$
, and, for a C*-algebra
![]() $A$
,
$A$
,
![]() $\tilde{\Delta }^1_A$
is the predeterminant (used in the definition of the de la Harpe-Skandalis determinant associated to the universal trace) that takes a piece-wise smooth path in
$\tilde{\Delta }^1_A$
is the predeterminant (used in the definition of the de la Harpe-Skandalis determinant associated to the universal trace) that takes a piece-wise smooth path in
![]() $U^0(A)$
beginning at the unit to an element of
$U^0(A)$
beginning at the unit to an element of
![]() $\textrm{Aff}\, T(A)$
. See Section 2.2 for details.
$\textrm{Aff}\, T(A)$
. See Section 2.2 for details.
Recall that the
![]() $K_0$
-group of a unital C*-algebra can be identified with the fundamental group
$K_0$
-group of a unital C*-algebra can be identified with the fundamental group
![]() $\pi _1(U_{\infty }^0(A))$
. Restricting to C*-algebras with sufficient
$\pi _1(U_{\infty }^0(A))$
. Restricting to C*-algebras with sufficient
![]() $K_0$
-regularity—by this we mean C*-algebras whose
$K_0$
-regularity—by this we mean C*-algebras whose
![]() $K_0$
-group can be realized as loops in the connected component of its unitary group—we get a map between
$K_0$
-group can be realized as loops in the connected component of its unitary group—we get a map between
![]() $K_0$
-groups and a map between spaces of continuous real-valued affine functions on the trace simplex which commute with the pairing.
$K_0$
-groups and a map between spaces of continuous real-valued affine functions on the trace simplex which commute with the pairing.
Corollary B (Corollary 3.6). Let
![]() $A,B$
be unital C*-algebras such that the canonical maps
$A,B$
be unital C*-algebras such that the canonical maps
are isomorphisms. If
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism, then there exists a bounded linear map
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism, then there exists a bounded linear map
![]() $\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
such that
$\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
such that

commutes, where
![]() $K_0(\theta )$
is the map induced by
$K_0(\theta )$
is the map induced by
![]() $\pi _1(\theta )$
together with the isomorphisms of (
1.2
).
$\pi _1(\theta )$
together with the isomorphisms of (
1.2
).
C*-algebras satisfying the above hypothesis are quite common—for example, C*-algebras having stable rank one [Reference Rieffel32] or that are
![]() $\mathcal{Z}$
-stable [Reference Jiang25] have this property. Viewing
$\mathcal{Z}$
-stable [Reference Jiang25] have this property. Viewing
![]() $\textrm{Aff}\, T(A)$
and
$\textrm{Aff}\, T(A)$
and
![]() $\textrm{Aff}\, T(B)$
as partially ordered real Banach spaces (under the uniform norm) with order units, it is not, however, true that
$\textrm{Aff}\, T(B)$
as partially ordered real Banach spaces (under the uniform norm) with order units, it is not, however, true that
![]() $\Lambda _\theta$
is unital or positive (see Example 3.4). This is remedied by adding stricter continuity assumptions on the homomorphism
$\Lambda _\theta$
is unital or positive (see Example 3.4). This is remedied by adding stricter continuity assumptions on the homomorphism
![]() $\theta$
(and possibly by replacing
$\theta$
(and possibly by replacing
![]() $\Lambda _\theta$
with
$\Lambda _\theta$
with
![]() $-\Lambda _\theta$
).
$-\Lambda _\theta$
).
When
![]() $\theta \,:\, U(A) \to U(B)$
is contractive, injective, and sends the circle to the circle, then we show (Lemma 4.3) that either
$\theta \,:\, U(A) \to U(B)$
is contractive, injective, and sends the circle to the circle, then we show (Lemma 4.3) that either
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
is unital and positive, and therefore,
$-\Lambda _\theta$
is unital and positive, and therefore,
![]() $\theta$
induces a map between
$\theta$
induces a map between
![]() $K$
-theory and traces in such a manner that respects the pairing (which in turn gives a map between Elliott invariants for certain simple C*-algebras). As a consequence, we can identify certain unitary subgroups with C*-subalgebras by using
$K$
-theory and traces in such a manner that respects the pairing (which in turn gives a map between Elliott invariants for certain simple C*-algebras). As a consequence, we can identify certain unitary subgroups with C*-subalgebras by using
![]() $K$
-theoretic classification of embeddings [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6].
$K$
-theoretic classification of embeddings [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6].
Theorem C (Corollary 4.13). Let
![]() $A$
be a unital, separable, simple, nuclear C*-algebra satisfying the UCT which is either
$A$
be a unital, separable, simple, nuclear C*-algebra satisfying the UCT which is either
![]() $\mathcal{Z}$
-stable or has stable rank one and
$\mathcal{Z}$
-stable or has stable rank one and
![]() $B$
be a unital, separable, simple, nuclear
$B$
be a unital, separable, simple, nuclear
![]() $\mathcal{Z}$
-stable C*-algebra. If there is a contractive injective group homomorphism
$\mathcal{Z}$
-stable C*-algebra. If there is a contractive injective group homomorphism
![]() $U(A) \to U(B)$
that maps the circle to the circle, then there is a unital embedding
$U(A) \to U(B)$
that maps the circle to the circle, then there is a unital embedding
![]() $A \hookrightarrow B$
.
$A \hookrightarrow B$
.
This paper is structured as follows. In Section 3, we use a continuous unitary group homomorphism to construct a map between spaces of continuous affine functions on the trace simplices and use the de la Harpe–Skandalis determinant to show that this map has several desirable properties with respect to the map induced on the fundamental groups of the unitary groups. In Section 4, we discuss how our map between spaces of affine functions respects or flips the order under certain continuity assumptions on the unitary group homomorphism. In Section 5, we discuss a slight general linear variant. We finish in Section 6 with some open questions.
2. Preliminaries and notation
2.1. Notation
For a group
![]() $G$
, we denote by
$G$
, we denote by
![]() $DG$
the derived subgroup of
$DG$
the derived subgroup of
![]() $G$
, that is
$G$
, that is
If
![]() $G$
has an underlying topology, we denote by
$G$
has an underlying topology, we denote by
![]() $CG$
the closure of
$CG$
the closure of
![]() $DG$
and
$DG$
and
![]() $G^0$
the connected component of the identity.
$G^0$
the connected component of the identity.
For a unital C*-algebra
![]() $A$
,
$A$
,
![]() $U(A)$
denotes the unitary group of
$U(A)$
denotes the unitary group of
![]() $A$
, while
$A$
, while
![]() $U^0(A)$
denotes the connected component of the identity in
$U^0(A)$
denotes the connected component of the identity in
![]() $U(A)$
. For
$U(A)$
. For
![]() $n \in \mathbb{N}$
, we write
$n \in \mathbb{N}$
, we write
![]() $U_n(A) \,:\!=\, U(M_n(A))$
,
$U_n(A) \,:\!=\, U(M_n(A))$
,
![]() $U_n^0(A) \,:\!=\, U^0(M_n(A))$
, and we set
$U_n^0(A) \,:\!=\, U^0(M_n(A))$
, and we set
to be the inductive limit with connecting maps
![]() $U_n(A) \ni u \mapsto u \oplus 1 \in U_{n+1}(A)$
. This makes
$U_n(A) \ni u \mapsto u \oplus 1 \in U_{n+1}(A)$
. This makes
![]() $U_\infty (A)$
both a topological space (with the inductive limit topology) and a group.Footnote
1
We have general linear analogs by replacing
$U_\infty (A)$
both a topological space (with the inductive limit topology) and a group.Footnote
1
We have general linear analogs by replacing
![]() $U$
with
$U$
with
![]() $GL$
, where
$GL$
, where
![]() $GL(A)$
denotes the group of invertible elements of
$GL(A)$
denotes the group of invertible elements of
![]() $A$
. Similarly, we define
$A$
. Similarly, we define
![]() $M_{\infty }(A) = \underset{\to }{\lim } \, M_n(A)$
(as an algebraic direct limit) with connecting maps
$M_{\infty }(A) = \underset{\to }{\lim } \, M_n(A)$
(as an algebraic direct limit) with connecting maps
![]() $x \mapsto x \oplus 0$
. If
$x \mapsto x \oplus 0$
. If
![]() $E$
is real Banach space and
$E$
is real Banach space and
![]() $\tau \,:\, A_{sa} \to E$
is a linear map that is tracial (i.e.,
$\tau \,:\, A_{sa} \to E$
is a linear map that is tracial (i.e.,
![]() $\tau (a^*a) = \tau (aa^*)$
for all
$\tau (a^*a) = \tau (aa^*)$
for all
![]() $a \in A$
), we extend this canonically to
$a \in A$
), we extend this canonically to
![]() $(M_{\infty }(A))_{sa}$
by setting
$(M_{\infty }(A))_{sa}$
by setting
![]() $\tau ((a_{ij})) \,:\!=\, \sum _i \tau (a_{ii})$
for
$\tau ((a_{ij})) \,:\!=\, \sum _i \tau (a_{ii})$
for
![]() $(a_{ij})\in (M_n(A)_{sa}$
.
$(a_{ij})\in (M_n(A)_{sa}$
.
We write
![]() $\pi _0(X)$
for the space of connected components of a topological space
$\pi _0(X)$
for the space of connected components of a topological space
![]() $X$
, and
$X$
, and
![]() $\pi _1(X)$
for the fundamental group of
$\pi _1(X)$
for the fundamental group of
![]() $X$
with distinguished base point. In our case, we will usually have
$X$
with distinguished base point. In our case, we will usually have
![]() $X = U_n(A)$
or
$X = U_n(A)$
or
![]() $X = U_n^0(A)$
, for
$X = U_n^0(A)$
, for
![]() $n \in \mathbb{N} \cup \{\infty \}$
, with the base point being the unit.
$n \in \mathbb{N} \cup \{\infty \}$
, with the base point being the unit.
For a unital C*-algebra
![]() $A$
, we let
$A$
, we let
![]() $K_0(A),K_1(A)$
be the topological
$K_0(A),K_1(A)$
be the topological
![]() $K$
-groups of
$K$
-groups of
![]() $A$
. We will often use the identification of
$A$
. We will often use the identification of
![]() $K_0(A)$
with the fundamental group
$K_0(A)$
with the fundamental group
![]() $\pi _1(U_{\infty }^0(A))$
(see e.g., [Reference Rørdam, Larsen and Laustsen33, Chapter 11.4]). The set of tracial states on
$\pi _1(U_{\infty }^0(A))$
(see e.g., [Reference Rørdam, Larsen and Laustsen33, Chapter 11.4]). The set of tracial states on
![]() $A$
will be denoted
$A$
will be denoted
![]() $T(A)$
, which is a Choquet simplex [Reference Sakai36, Theorem 3.1.18], and we denote by
$T(A)$
, which is a Choquet simplex [Reference Sakai36, Theorem 3.1.18], and we denote by
![]() $\textrm{Aff}\, T(A)$
the set of continuous affine functions
$\textrm{Aff}\, T(A)$
the set of continuous affine functions
![]() $T(A) \to \mathbb{R}$
, which is an interpolation group with order unit (see [Reference Goodearl21, Chapter 11]). For unital
$T(A) \to \mathbb{R}$
, which is an interpolation group with order unit (see [Reference Goodearl21, Chapter 11]). For unital
![]() $A$
, the pairing map
$A$
, the pairing map
![]() $\rho _A\,:\, K_0(A) \to \textrm{Aff}\, T(A)$
is defined as follows: if
$\rho _A\,:\, K_0(A) \to \textrm{Aff}\, T(A)$
is defined as follows: if
![]() $x \in K_0(A)$
, we can write
$x \in K_0(A)$
, we can write
![]() $x = [p] - [q]$
where
$x = [p] - [q]$
where
![]() $p,q \in M_n(A)$
are projections, and then
$p,q \in M_n(A)$
are projections, and then
2.2. The de la Harpe–Skandalis determinant and Thomsen’s variant
We recall the definition of the unitary variant of the de la Harpe–Skandalis determinant [Reference de la Harpe and Skandalis12] (see [Reference de la Harpe11] for a more in-depth exposition). By a bounded trace, we mean a bounded linear map
![]() $\tau \,:\, A_{sa} \to E$
, where
$\tau \,:\, A_{sa} \to E$
, where
![]() $E$
is a real Banach space, such that
$E$
is a real Banach space, such that
![]() $\tau (a^*a) = \tau (aa^*)$
for all
$\tau (a^*a) = \tau (aa^*)$
for all
![]() $a \in A$
. For
$a \in A$
. For
![]() $n \in \mathbb{N} \cup \{\infty \}$
, a bounded trace
$n \in \mathbb{N} \cup \{\infty \}$
, a bounded trace
![]() $\tau \,:\, A_{sa} \to E$
, and a piece-wise smooth path
$\tau \,:\, A_{sa} \to E$
, and a piece-wise smooth path
![]() $\xi \,:\, [0,1] \to U_n(A)$
, set
$\xi \,:\, [0,1] \to U_n(A)$
, set
where this integral is just the Riemann integral in
![]() $E$
.Footnote
2
We state the unitary variant of [Reference de la Harpe and Skandalis12, Lemme 1].
$E$
.Footnote
2
We state the unitary variant of [Reference de la Harpe and Skandalis12, Lemme 1].
Proposition 2.1.
Let
![]() $\tau \,:\, A_{sa} \to E$
be a bounded trace and
$\tau \,:\, A_{sa} \to E$
be a bounded trace and
![]() $n \in \mathbb{N} \cup \{\infty \}$
. The map
$n \in \mathbb{N} \cup \{\infty \}$
. The map
![]() $\tilde{\Delta }_\tau ^n$
, which takes a piece-wise smooth path in
$\tilde{\Delta }_\tau ^n$
, which takes a piece-wise smooth path in
![]() $U_n^0(A)$
to an element in
$U_n^0(A)$
to an element in
![]() $E$
, has the following four properties:
$E$
, has the following four properties:
-
1. it takes pointwise products to sums: if
 $\xi _1,\xi _2$
are two piece-wise smooth paths, then
(2.5)where
$\xi _1,\xi _2$
are two piece-wise smooth paths, then
(2.5)where \begin{equation} \tilde{\Delta }_\tau ^n(\xi _1\xi _2) = \tilde{\Delta }_\tau ^n(\xi _1) + \tilde{\Delta }_\tau ^n(\xi _2), \end{equation}
\begin{equation} \tilde{\Delta }_\tau ^n(\xi _1\xi _2) = \tilde{\Delta }_\tau ^n(\xi _1) + \tilde{\Delta }_\tau ^n(\xi _2), \end{equation}
 $\xi _1\xi _2$
is the piece-wise smooth path
$\xi _1\xi _2$
is the piece-wise smooth path
 $t \mapsto \xi _1(t)\xi _2(t)$
from
$t \mapsto \xi _1(t)\xi _2(t)$
from
 $\xi _1(0)\xi _2(0)$
to
$\xi _1(0)\xi _2(0)$
to
 $\xi _1(1)\xi _2(1)$
;
$\xi _1(1)\xi _2(1)$
;
-
2. if
 $\|\xi (t) - 1\| \lt 1$
for all
$\|\xi (t) - 1\| \lt 1$
for all
 $t \in [0,1]$
, then
(2.6)
$t \in [0,1]$
, then
(2.6) \begin{equation} 2\pi i \tilde{\Delta }_\tau ^n(\xi ) = \tau \big (\log \xi (1) - \log \xi (0)\big ); \end{equation}
\begin{equation} 2\pi i \tilde{\Delta }_\tau ^n(\xi ) = \tau \big (\log \xi (1) - \log \xi (0)\big ); \end{equation}
-
3.
 $\tilde{\Delta }_\tau ^n(\xi )$
depends only on the continuous homotopy class of
$\tilde{\Delta }_\tau ^n(\xi )$
depends only on the continuous homotopy class of
 $\xi$
;
$\xi$
; -
4. if
 $p \in M_n(A)$
is a projection, then the path
$p \in M_n(A)$
is a projection, then the path
 $\xi _p\,:\, [0,1] \to U_n^0(A)$
given by
$\xi _p\,:\, [0,1] \to U_n^0(A)$
given by
 $\xi _p(t) \,:\!=\, pe^{2\pi i t} + (1-p)$
satisfies
$\xi _p(t) \,:\!=\, pe^{2\pi i t} + (1-p)$
satisfies
 $\tilde{\Delta }_\tau ^n(p) = \tau (p)$
.
$\tilde{\Delta }_\tau ^n(p) = \tau (p)$
.
The de la Harpe–Skandalis determinant associated to
![]() $\tau$
(at the
$\tau$
(at the
![]() $n^{\text{th}}$
level) is then the map
$n^{\text{th}}$
level) is then the map
given by
![]() $\Delta _\tau ^n(x) \,:\!=\, \left[\tilde{\Delta }_\tau ^n(\xi _x)\right]$
where
$\Delta _\tau ^n(x) \,:\!=\, \left[\tilde{\Delta }_\tau ^n(\xi _x)\right]$
where
![]() $\xi _x$
is any piece-wise smooth path
$\xi _x$
is any piece-wise smooth path
![]() $\xi _x\,:\, [0,1] \to U_n^0(A)$
from 1 to
$\xi _x\,:\, [0,1] \to U_n^0(A)$
from 1 to
![]() $x$
. This is a well-defined group homomorphism (using Proposition 2.1) to an abelian group and therefore factors through the derived group, i.e.,
$x$
. This is a well-defined group homomorphism (using Proposition 2.1) to an abelian group and therefore factors through the derived group, i.e.,
![]() $DU_n^0(A) \subseteq \ker \Delta _\tau ^n$
. For the
$DU_n^0(A) \subseteq \ker \Delta _\tau ^n$
. For the
![]() $n = \infty$
case, we just write
$n = \infty$
case, we just write
![]() $\tilde{\Delta }_\tau$
and
$\tilde{\Delta }_\tau$
and
![]() $\Delta _\tau$
for
$\Delta _\tau$
for
![]() $\tilde{\Delta }_\tau ^{\infty }$
and
$\tilde{\Delta }_\tau ^{\infty }$
and
![]() $\Delta _\tau ^{\infty }$
, respectively.
$\Delta _\tau ^{\infty }$
, respectively.
We will often be interested in the universal trace
![]() $\text{Tr}_A\,:\, A_{sa} \to \textrm{Aff}\, T(A)$
, which is given by
$\text{Tr}_A\,:\, A_{sa} \to \textrm{Aff}\, T(A)$
, which is given by
![]() $\text{Tr}_A(a) \,:\!=\, \hat{a}$
, where
$\text{Tr}_A(a) \,:\!=\, \hat{a}$
, where
![]() $\hat{a} \in \textrm{Aff}\, T(A)$
is the function given by
$\hat{a} \in \textrm{Aff}\, T(A)$
is the function given by
![]() $\hat{a}(\tau ) \,:\!=\, \tau (a)$
for
$\hat{a}(\tau ) \,:\!=\, \tau (a)$
for
![]() $\tau \in T(A)$
. We note that in this case, for
$\tau \in T(A)$
. We note that in this case, for
![]() $[x] \in K_0(A)$
, we have that
$[x] \in K_0(A)$
, we have that
![]() $\text{Tr}(x) = \rho _A([x])$
. When considering the universal trace, we will write
$\text{Tr}(x) = \rho _A([x])$
. When considering the universal trace, we will write
![]() $\Delta ^n$
and
$\Delta ^n$
and
![]() $\Delta$
for
$\Delta$
for
![]() $\Delta _{\text{Tr}}^n$
and
$\Delta _{\text{Tr}}^n$
and
![]() $\Delta _{\text{Tr}}^{\infty }$
, respectively. If the C*-algebra needs to be specified, we write
$\Delta _{\text{Tr}}^{\infty }$
, respectively. If the C*-algebra needs to be specified, we write
![]() $\Delta _A^n$
or
$\Delta _A^n$
or
![]() $\Delta _A$
.
$\Delta _A$
.
Proposition 2.2.
Let
![]() $n \in \mathbb{N} \cup \{\infty \}$
. Every continuous path
$n \in \mathbb{N} \cup \{\infty \}$
. Every continuous path
![]() $\xi \,:\, [0,1] \to U_n(A)$
is homotopic to a piece-wise smooth path (even a piece-wise smooth exponential path if we are in
$\xi \,:\, [0,1] \to U_n(A)$
is homotopic to a piece-wise smooth path (even a piece-wise smooth exponential path if we are in
![]() $U_n^0(A)$
). Moreover, there exists
$U_n^0(A)$
). Moreover, there exists
![]() $a \in A_{sa}$
such that
$a \in A_{sa}$
such that
![]() $\tilde{\Delta }_\omega ^n(\xi ) = \omega (a)$
whenever
$\tilde{\Delta }_\omega ^n(\xi ) = \omega (a)$
whenever
![]() $\omega \,:\, A_{sa} \to E$
is a bounded trace.
$\omega \,:\, A_{sa} \to E$
is a bounded trace.
In particular, as
![]() $\tilde{\Delta }^n$
is homotopy invariant, it makes sense to apply
$\tilde{\Delta }^n$
is homotopy invariant, it makes sense to apply
![]() $\tilde{\Delta }^n$
to any continuous path.
$\tilde{\Delta }^n$
to any continuous path.
Proof. This is essentially [Reference de la Harpe and Skandalis12, Lemme 3]. Take a continuous path
![]() $\xi \,:\, [0,1] \to U_n(A)$
and choose
$\xi \,:\, [0,1] \to U_n(A)$
and choose
![]() $k$
such that
$k$
such that
 \begin{equation} \left \|\xi \left(\frac{j-1}{k}\right)^{-1}\xi \left(\frac{j}{k}\right) - 1\right \| \lt 1 \text{ for all } j=1,\dots,k. \end{equation}
\begin{equation} \left \|\xi \left(\frac{j-1}{k}\right)^{-1}\xi \left(\frac{j}{k}\right) - 1\right \| \lt 1 \text{ for all } j=1,\dots,k. \end{equation}
Then taking
 \begin{equation} a_j \,:\!=\, \frac{1}{2\pi i}\log \left (\xi \left(\frac{j-1}{k}\right)^{-1}\xi \left(\frac{j}{k}\right)\right ), j=1,\dots,k, \end{equation}
\begin{equation} a_j \,:\!=\, \frac{1}{2\pi i}\log \left (\xi \left(\frac{j-1}{k}\right)^{-1}\xi \left(\frac{j}{k}\right)\right ), j=1,\dots,k, \end{equation}
![]() $\xi$
will be homotopic to the path
$\xi$
will be homotopic to the path
We note that
![]() $\tilde{\Delta }_\tau ^n(\eta ) = \sum _{j=1}^k \tau (a_j)$
. Indeed, for simplicity denote by
$\tilde{\Delta }_\tau ^n(\eta ) = \sum _{j=1}^k \tau (a_j)$
. Indeed, for simplicity denote by
Then
 \begin{equation} \begin{split} \tilde{\Delta }_\omega ^n(\xi ) &= \tilde{\Delta }_\omega ^n(\eta ) \\ &=\sum _{j=1}^k \int _{\frac{j-1}{k}}^{\frac{j}{k}}\tau \left (\frac{1}{2\pi i}X_j 2\pi i k a_jY_jY_j^*X_j^*\right ) dt \\ &= \sum _{j=1}^k \int _{\frac{j-1}{k}}^{\frac{j}{k}}k\tau (a_j) dt \\ &= \sum _{j=1}^k \tau (a_j). \end{split} \end{equation}
\begin{equation} \begin{split} \tilde{\Delta }_\omega ^n(\xi ) &= \tilde{\Delta }_\omega ^n(\eta ) \\ &=\sum _{j=1}^k \int _{\frac{j-1}{k}}^{\frac{j}{k}}\tau \left (\frac{1}{2\pi i}X_j 2\pi i k a_jY_jY_j^*X_j^*\right ) dt \\ &= \sum _{j=1}^k \int _{\frac{j-1}{k}}^{\frac{j}{k}}k\tau (a_j) dt \\ &= \sum _{j=1}^k \tau (a_j). \end{split} \end{equation}
If we take
![]() $a \,:\!=\,{\text{tr}}(a^{\prime})$
, where
$a \,:\!=\,{\text{tr}}(a^{\prime})$
, where
![]() $a^{\prime} = \sum _{j=1}^k a_j$
(here
$a^{\prime} = \sum _{j=1}^k a_j$
(here
![]() ${\text{tr}}\,:\, M_{\infty }(A) \to A$
is the unnormalized trace), we see that
${\text{tr}}\,:\, M_{\infty }(A) \to A$
is the unnormalized trace), we see that
![]() $\tilde{\Delta }_\omega ^n(\xi ) = \omega (a)$
.
$\tilde{\Delta }_\omega ^n(\xi ) = \omega (a)$
.
Let
![]() $A_0$
consist of elements
$A_0$
consist of elements
![]() $a \in A_{sa}$
satisfying
$a \in A_{sa}$
satisfying
![]() $\tau (a) = 0$
for all
$\tau (a) = 0$
for all
![]() $\tau \in T(A)$
. This is a norm-closed real subspace of
$\tau \in T(A)$
. This is a norm-closed real subspace of
![]() $A_{sa}$
such that
$A_{sa}$
such that
![]() $A_0 \subseteq \overline{[A,A]}$
, and there is an isometric identification
$A_0 \subseteq \overline{[A,A]}$
, and there is an isometric identification
![]() $A_{sa}/A_0 \simeq \textrm{Aff}\, T(A)$
sending an element
$A_{sa}/A_0 \simeq \textrm{Aff}\, T(A)$
sending an element
![]() $[a]$
to
$[a]$
to
![]() $\widehat{a}$
. Indeed, it is not hard to see that the map
$\widehat{a}$
. Indeed, it is not hard to see that the map
![]() $A_{sa}/A_0 \to \textrm{Aff}\, T(A)$
given by
$A_{sa}/A_0 \to \textrm{Aff}\, T(A)$
given by
![]() $[a] \mapsto \hat{a}$
is a well-defined
$[a] \mapsto \hat{a}$
is a well-defined
![]() $\mathbb{R}$
-linear map. Moreover [Reference Cuntz and Pedersen8, Theorem 2.9], together with a convexity argument, gives that this is isometric identification. To see that we have all the real-valued affine functions, we note that the image of this map contains constant functions and separates points, so [Reference Goodearl21, Corollary 7.4] gives that the image is dense and therefore all of
$\mathbb{R}$
-linear map. Moreover [Reference Cuntz and Pedersen8, Theorem 2.9], together with a convexity argument, gives that this is isometric identification. To see that we have all the real-valued affine functions, we note that the image of this map contains constant functions and separates points, so [Reference Goodearl21, Corollary 7.4] gives that the image is dense and therefore all of
![]() $\textrm{Aff}\, T(A)$
(since this is an isometry). We freely identify
$\textrm{Aff}\, T(A)$
(since this is an isometry). We freely identify
![]() $A_{sa}/A_0$
with
$A_{sa}/A_0$
with
![]() $\textrm{Aff}\, T(A)$
.
$\textrm{Aff}\, T(A)$
.
2.3. Thomsen’s variant
Thomsen’s variant of the de la Harpe–Skandalis determinant is the Hausdorffized version, taking into account the closure of the image of the homotopy groups. For a bounded trace
![]() $\tau \,:\, A_{sa} \to E$
, we consider the map
$\tau \,:\, A_{sa} \to E$
, we consider the map
given by
![]() $\bar{\Delta }_\tau ^n(x) \,:\!=\, \left[\tilde{\Delta }_\tau ^n(\xi _x)\right]$
where
$\bar{\Delta }_\tau ^n(x) \,:\!=\, \left[\tilde{\Delta }_\tau ^n(\xi _x)\right]$
where
![]() $\xi _x\,:\, [0,1] \to U_n^0(A)$
is any piece-wise smooth path from 1 to
$\xi _x\,:\, [0,1] \to U_n^0(A)$
is any piece-wise smooth path from 1 to
![]() $x \in U_n^0(A)$
. This is similar to the map
$x \in U_n^0(A)$
. This is similar to the map
![]() $\Delta _\tau ^n$
, except the codomain is now the quotient by the closure of the image of the fundamental group under the predeterminant (i.e., the Hausdorffization of the codomain). When considering the universal trace, we just write
$\Delta _\tau ^n$
, except the codomain is now the quotient by the closure of the image of the fundamental group under the predeterminant (i.e., the Hausdorffization of the codomain). When considering the universal trace, we just write
![]() $\overline \Delta ^n$
for
$\overline \Delta ^n$
for
![]() $\overline \Delta _{\text{Tr}}^n$
and
$\overline \Delta _{\text{Tr}}^n$
and
![]() $\overline \Delta$
for
$\overline \Delta$
for
![]() $\overline \Delta _{\text{Tr}}^{\infty }$
. If the C*-algebra needs to be specified, we write
$\overline \Delta _{\text{Tr}}^{\infty }$
. If the C*-algebra needs to be specified, we write
![]() $\overline \Delta _A^n$
or
$\overline \Delta _A^n$
or
![]() $\overline \Delta _A$
.
$\overline \Delta _A$
.
If one considers the universal trace, the kernel of
![]() $\overline \Delta ^n$
can be identified with
$\overline \Delta ^n$
can be identified with
![]() $CU_n^0(A)$
(where the closure is taken with respect to the inductive limit topology in the
$CU_n^0(A)$
(where the closure is taken with respect to the inductive limit topology in the
![]() $n = \infty$
case).
$n = \infty$
case).
Lemma 2.3 (Lemma 3.1, [Reference Thomsen39]). Let
![]() $A$
be a unital C*-algebra. Then
$A$
be a unital C*-algebra. Then
It is not in general true that the kernel of
![]() $\Delta ^n$
can be identified with the derived group
$\Delta ^n$
can be identified with the derived group
![]() $DU_n^0(A)$
, although there are several positive results [Reference de la Harpe and Skandalis13, Reference Ng26, Reference Ng and Robert27, Reference Thomsen38].
$DU_n^0(A)$
, although there are several positive results [Reference de la Harpe and Skandalis13, Reference Ng26, Reference Ng and Robert27, Reference Thomsen38].
It immediately follows that the quotient of
![]() $U_n^0(A)$
by the closure of the commutator subgroup (under the inductive limit topology in the
$U_n^0(A)$
by the closure of the commutator subgroup (under the inductive limit topology in the
![]() $n = \infty$
case) can be identified with a quotient of
$n = \infty$
case) can be identified with a quotient of
![]() $\textrm{Aff}\, T(A)$
.
$\textrm{Aff}\, T(A)$
.
Theorem 2.4 (Theorem 3.2, [Reference Thomsen39]).
![]() $\overline \Delta ^n$
gives a homeomorphic group isomorphism
$\overline \Delta ^n$
gives a homeomorphic group isomorphism
for every
![]() $n \in \mathbb{N} \cup \{\infty \}$
. In particular,
$n \in \mathbb{N} \cup \{\infty \}$
. In particular,
2.4. The
 $KT_u$
invariant
$KT_u$
invariant
Following [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6], for a unital C*-algebra, we let
be the invariant consisting of the
![]() $K_0$
group, the position of the unit in
$K_0$
group, the position of the unit in
![]() $K_0$
, the
$K_0$
, the
![]() $K_1$
group, the pairing between
$K_1$
group, the pairing between
![]() $K_0$
and traces, and the continuous real-valued affine functions on the trace simplex (viewed as a partially ordered Banach space with order unit). For two unital C*-algebras
$K_0$
and traces, and the continuous real-valued affine functions on the trace simplex (viewed as a partially ordered Banach space with order unit). For two unital C*-algebras
![]() $A,B$
, a
$A,B$
, a
![]() $KT_u$
morphism
$KT_u$
morphism
will be a triple
![]() $(\alpha _0,\alpha _1,\gamma )$
consisting of
$(\alpha _0,\alpha _1,\gamma )$
consisting of
![]() $\alpha _0\,:\, K_0(A) \to K_0(B)$
a group homomorphism such that
$\alpha _0\,:\, K_0(A) \to K_0(B)$
a group homomorphism such that
![]() $\alpha _0([1_A]_0) = [1_B]_0$
,
$\alpha _0([1_A]_0) = [1_B]_0$
,
![]() $\alpha _1\,:\, K_1(A) \to K_1(B)$
a group homomorphism, and
$\alpha _1\,:\, K_1(A) \to K_1(B)$
a group homomorphism, and
![]() $\gamma \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a unital positive map such that
$\gamma \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a unital positive map such that

commutes.
We note that for large classes of unital simple C*-algebras—for example, the class of unital, simple, separable, nuclear
![]() $\mathcal{Z}$
-stable C*-algebras satisfying the UCT—
$\mathcal{Z}$
-stable C*-algebras satisfying the UCT—
![]() $KT_u(\cdot )$
recovers the Elliott invariant.
$KT_u(\cdot )$
recovers the Elliott invariant.
3. Continuous unitary group homomorphisms and traces
Throughout,
![]() $A$
and
$A$
and
![]() $B$
will be unital C*-algebras with nonempty trace simplices, and
$B$
will be unital C*-algebras with nonempty trace simplices, and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
will denote a uniformly continuous group homomorphism between the connected components of the identities in the respective unitary groups. We will specify any additional assumptions as we go along. As
$\theta \,:\, U^0(A) \to U^0(B)$
will denote a uniformly continuous group homomorphism between the connected components of the identities in the respective unitary groups. We will specify any additional assumptions as we go along. As
![]() $\theta$
is a continuous group homomorphism, it send commutators to commutators and limits of commutators to limits of commutators. Thus, there are induced group homomorphisms
$\theta$
is a continuous group homomorphism, it send commutators to commutators and limits of commutators to limits of commutators. Thus, there are induced group homomorphisms
Thomsen’s isomorphism [Reference Thomsen39, Theorem 3] then brings about maps between quotients of
![]() $\textrm{Aff}\, T(A)$
and
$\textrm{Aff}\, T(A)$
and
![]() $\textrm{Aff}\, T(B)$
:
$\textrm{Aff}\, T(B)$
:

In a similar vein, when
![]() $DU^0(A) = \ker \Delta _A^1$
and
$DU^0(A) = \ker \Delta _A^1$
and
![]() $DU^0(B) = \ker \Delta _B^1$
, there is a purely algebraic variant of the above diagram:
$DU^0(B) = \ker \Delta _B^1$
, there is a purely algebraic variant of the above diagram:

In fact, there is always a diagram as above with
![]() $DU^0(A)$
and
$DU^0(A)$
and
![]() $DU^0(B)$
replaced with
$DU^0(B)$
replaced with
![]() $\ker \Delta _A^1$
and
$\ker \Delta _A^1$
and
![]() $\ker \Delta _B^1$
, respectively, by Proposition 3.5(3). That is, whether or not the kernel of the determinant agrees with the commutator subgroup of the connected component of the identity, we have:
$\ker \Delta _B^1$
, respectively, by Proposition 3.5(3). That is, whether or not the kernel of the determinant agrees with the commutator subgroup of the connected component of the identity, we have:

The diagram in (3.3) is just a special case of (3.4).
In the setting where
![]() $\pi _1\big(U^0(A)\big) \to K_0(A)$
and
$\pi _1\big(U^0(A)\big) \to K_0(A)$
and
![]() $\pi _1\big(U^0(B)\big) \to K_0(B)$
are surjections, we have induced maps between quotients
$\pi _1\big(U^0(B)\big) \to K_0(B)$
are surjections, we have induced maps between quotients
in the respective Hausdorffized and non-Hausdorffized settings.
One question to be answered is whether or not we can lift the maps on the right of (3.2) and (3.4) to maps
![]() $\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
. These spaces have further structure as dimension groups with order units [Reference Goodearl21, Chapter 7], so we would like to be able to alter the lift to get a map which is unital and positive. We show that we can always lift this map, and altering it to be unital and positive is possible under a certain continuity assumption on
$\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
. These spaces have further structure as dimension groups with order units [Reference Goodearl21, Chapter 7], so we would like to be able to alter the lift to get a map which is unital and positive. We show that we can always lift this map, and altering it to be unital and positive is possible under a certain continuity assumption on
![]() $\theta$
.
$\theta$
.
If we further assume that
![]() $K_0(A) \simeq \pi _1\big(U^0(A)\big)$
and
$K_0(A) \simeq \pi _1\big(U^0(A)\big)$
and
![]() $K_0(B) \simeq \pi _1\big(U^0(B)\big)$
in the canonical way (which is true in the presence of
$K_0(B) \simeq \pi _1\big(U^0(B)\big)$
in the canonical way (which is true in the presence of
![]() $\mathcal{Z}$
-stability by [Reference Jiang25] or stable rank one [Reference Rieffel32]), we would like this map to be compatible with the group homomorphism
$\mathcal{Z}$
-stability by [Reference Jiang25] or stable rank one [Reference Rieffel32]), we would like this map to be compatible with the group homomorphism
arising from the diagram

By compatible, we mean that

commutes, where the map on the right is the lift coming from maps induced by (3.2) and (3.4). If our map between spaces of affine continuous functions is not unital and positive, but we can alter it accordingly, we must do the same to our map between
![]() $K_0$
. We would still have a commuting diagram as above, but it would give that maps induced on
$K_0$
. We would still have a commuting diagram as above, but it would give that maps induced on
![]() $K_0(\cdot )$
and
$K_0(\cdot )$
and
![]() $\textrm{Aff}\, T(\cdot )$
respect the pairing.
$\textrm{Aff}\, T(\cdot )$
respect the pairing.
Stone’s theorem [Reference Conway7, Section X.5] allows one to recover from a strongly continuous one parameter family
![]() $U(t)$
of unitaries a (possibly unbounded) self-adjoint operator
$U(t)$
of unitaries a (possibly unbounded) self-adjoint operator
![]() $X$
such that
$X$
such that
![]() $U(t) = e^{itX}$
for all
$U(t) = e^{itX}$
for all
![]() $t \in \mathbb{R}$
. If it is a norm-continuous one parameter family of unitaries, one can recover a bounded self-adjoint operator
$t \in \mathbb{R}$
. If it is a norm-continuous one parameter family of unitaries, one can recover a bounded self-adjoint operator
![]() $X$
, and
$X$
, and
![]() $X$
will lie in the C*-algebra generated by the unitaries. The use of Stone’s theorem to deduce that continuous group homomorphisms between unitary groups send exponentials to exponentials is not new. Sakai used it in the 1950s in order to show that a norm-continuous group isomorphism between unitary groups of AW*-algebras are induced by a *-isomorphism or conjugate-linear *-isomorphism between the algebras themselves [Reference Sakai35]. More recently, this sort of idea has been used to understand how the metric structure of the unitary groups can be related to the Jordan *-algebra structure of the algebras [Reference Hatori and Molnár24].
$X$
will lie in the C*-algebra generated by the unitaries. The use of Stone’s theorem to deduce that continuous group homomorphisms between unitary groups send exponentials to exponentials is not new. Sakai used it in the 1950s in order to show that a norm-continuous group isomorphism between unitary groups of AW*-algebras are induced by a *-isomorphism or conjugate-linear *-isomorphism between the algebras themselves [Reference Sakai35]. More recently, this sort of idea has been used to understand how the metric structure of the unitary groups can be related to the Jordan *-algebra structure of the algebras [Reference Hatori and Molnár24].
Lemma 3.1.
Let
![]() $A,B$
be unital C*-algebras and
$A,B$
be unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism. Suppose that
$\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism. Suppose that
![]() $a \in A_{sa}$
and represent
$a \in A_{sa}$
and represent
![]() $B \subseteq \mathcal{B}(\mathcal{H})$
faithfully. Then
$B \subseteq \mathcal{B}(\mathcal{H})$
faithfully. Then
![]() $\left(\theta \left(e^{2\pi i t a}\right)\right)_{t \in \mathbb{R}}$
is a one-parameter norm-continuous family of unitaries, and consequently is of the form
$\left(\theta \left(e^{2\pi i t a}\right)\right)_{t \in \mathbb{R}}$
is a one-parameter norm-continuous family of unitaries, and consequently is of the form
![]() $\left(e^{2\pi i t b}\right)_{t \in \mathbb{R}}$
for a unique
$\left(e^{2\pi i t b}\right)_{t \in \mathbb{R}}$
for a unique
![]() $b \in B_{sa}$
.
$b \in B_{sa}$
.
Proof. Using the fact that
![]() $\theta$
is a norm-continuous homomorphism,
$\theta$
is a norm-continuous homomorphism,
![]() $t \mapsto \theta \left(e^{2\pi i t a}\right)$
is a norm-continuous one-parameter family of unitaries. Stone’s theorem gives that there is a unique self-adjoint
$t \mapsto \theta \left(e^{2\pi i t a}\right)$
is a norm-continuous one-parameter family of unitaries. Stone’s theorem gives that there is a unique self-adjoint
![]() $b \in \mathcal{B}(\mathcal{H})$
such that
$b \in \mathcal{B}(\mathcal{H})$
such that
![]() $\theta \left(e^{2\pi i ta}\right) = e^{2\pi i tb}$
for all
$\theta \left(e^{2\pi i ta}\right) = e^{2\pi i tb}$
for all
![]() $t \in \mathbb{R}$
. The boundedness of
$t \in \mathbb{R}$
. The boundedness of
![]() $b$
follows from norm-continuity, and the uniqueness follows from the fact that
$b$
follows from norm-continuity, and the uniqueness follows from the fact that
![]() $b = \frac{1}{2\pi i t_0} \log \theta \left(e^{2\pi i a t_0}\right)$
for sufficiently small
$b = \frac{1}{2\pi i t_0} \log \theta \left(e^{2\pi i a t_0}\right)$
for sufficiently small
![]() $t_0 \gt 0$
. This also gives that
$t_0 \gt 0$
. This also gives that
![]() $b \in B$
by functional calculus.
$b \in B$
by functional calculus.
Let
![]() $S_\theta \,:\, A_{sa} \to B_{sa}$
be defined via the correspondence given above:
$S_\theta \,:\, A_{sa} \to B_{sa}$
be defined via the correspondence given above:
Then
![]() $S_\theta$
is a bounded
$S_\theta$
is a bounded
![]() $\mathbb{R}$
-linear map (see [Reference Hatori and Molnár24, Reference Sakai35], or note that it is easy to see that its kernel is closed). It is also easily checked to respect commutation, and that its canonical extension to a map from
$\mathbb{R}$
-linear map (see [Reference Hatori and Molnár24, Reference Sakai35], or note that it is easy to see that its kernel is closed). It is also easily checked to respect commutation, and that its canonical extension to a map from
![]() $A$
to
$A$
to
![]() $B$
actually sends commutators to commutators, although we will not explicitly use this. Recall that for a C*-algebra
$B$
actually sends commutators to commutators, although we will not explicitly use this. Recall that for a C*-algebra
![]() $A$
,
$A$
,
![]() $A_0$
denotes the set of self-adjoint elements that vanish on every tracial state.
$A_0$
denotes the set of self-adjoint elements that vanish on every tracial state.
Lemma 3.2.
If
![]() $\theta \,:\,U^0(A) \to U^0(B)$
is a continuous group homomorphism, then
$\theta \,:\,U^0(A) \to U^0(B)$
is a continuous group homomorphism, then
![]() $S_\theta$
is a bounded linear map and the following hold.
$S_\theta$
is a bounded linear map and the following hold.
-
1. If
 $\theta$
is injective, then
$\theta$
is injective, then
 $S_\theta$
is injective.
$S_\theta$
is injective.
-
2. If
 $\theta$
is a homeomorphism, then
$\theta$
is a homeomorphism, then
 $S_\theta$
is bijective.
$S_\theta$
is bijective.
Proof. As already remarked,
![]() $S_\theta$
is bounded. Assuming that
$S_\theta$
is bounded. Assuming that
![]() $\theta$
is injective, suppose that
$\theta$
is injective, suppose that
![]() $S_\theta (a) = S_\theta (b)$
. Then
$S_\theta (a) = S_\theta (b)$
. Then
for all
![]() $t \in \mathbb{R}$
. Injectivity of
$t \in \mathbb{R}$
. Injectivity of
![]() $\theta$
gives that
$\theta$
gives that
![]() $e^{2\pi i t a} = e^{2\pi i t b}$
for all
$e^{2\pi i t a} = e^{2\pi i t b}$
for all
![]() $t \in \mathbb{R}$
. But this implies that
$t \in \mathbb{R}$
. But this implies that
![]() $a = b$
since we can take
$a = b$
since we can take
![]() $t$
appropriately close to 0 and take logarithms.
$t$
appropriately close to 0 and take logarithms.
Now if we further assume that
![]() $\theta$
is a homeomorphism, then
$\theta$
is a homeomorphism, then
![]() $(\theta ^{-1}\left(e^{2\pi i t b}\right))_{t \in \mathbb{R}} \subseteq U^0(A)$
is a norm-continuous one-parameter family of unitaries which we can write as
$(\theta ^{-1}\left(e^{2\pi i t b}\right))_{t \in \mathbb{R}} \subseteq U^0(A)$
is a norm-continuous one-parameter family of unitaries which we can write as
![]() $\left(e^{2\pi i t a}\right)_{t \in \mathbb{R}}$
for some
$\left(e^{2\pi i t a}\right)_{t \in \mathbb{R}}$
for some
![]() $a \in A_{sa}$
. But then
$a \in A_{sa}$
. But then
Thus,
![]() $S_\theta (a) = b$
by the uniqueness in Lemma 3.1.
$S_\theta (a) = b$
by the uniqueness in Lemma 3.1.
Recall that a linear map
![]() $\tau \,:\, A_{sa} \to E$
, where
$\tau \,:\, A_{sa} \to E$
, where
![]() $E$
is a real Banach space, is a bounded trace is if it is a bounded
$E$
is a real Banach space, is a bounded trace is if it is a bounded
![]() $\mathbb{R}$
-linear map such that
$\mathbb{R}$
-linear map such that
![]() $\tau (a^*a) = \tau (aa^*)$
for all
$\tau (a^*a) = \tau (aa^*)$
for all
![]() $a \in A$
. Note that this is equivalent to
$a \in A$
. Note that this is equivalent to
![]() $\tau \circ \text{Ad}_u = \tau$
for all
$\tau \circ \text{Ad}_u = \tau$
for all
![]() $u \in U(A)$
– to see this, follow the steps in [Reference Rørdam, Larsen and Laustsen33, Exercise 3.6] together with a complexification argument. This is further equivalent to
$u \in U(A)$
– to see this, follow the steps in [Reference Rørdam, Larsen and Laustsen33, Exercise 3.6] together with a complexification argument. This is further equivalent to
![]() $\tau \circ \text{Ad}_u = \tau$
for all
$\tau \circ \text{Ad}_u = \tau$
for all
![]() $u \in U^0(A)$
(as one can write every element in a C*-algebra as the linear combination of four unitaries, each of which can be made to not have full spectrum).
$u \in U^0(A)$
(as one can write every element in a C*-algebra as the linear combination of four unitaries, each of which can be made to not have full spectrum).
Proposition 3.3.
Let
![]() $\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism,
$\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism,
![]() $E$
be a real Banach space and
$E$
be a real Banach space and
![]() $\tau \,:\, B_{sa} \to E$
a bounded trace. Then
$\tau \,:\, B_{sa} \to E$
a bounded trace. Then
![]() $\tau \circ S_\theta \,:\, A_{sa} \to E$
is a bounded trace. In particular,
$\tau \circ S_\theta \,:\, A_{sa} \to E$
is a bounded trace. In particular,
![]() $S_\theta (A_0) \subseteq B_0$
and
$S_\theta (A_0) \subseteq B_0$
and
![]() $S_\theta$
induce a bounded
$S_\theta$
induce a bounded
![]() $\mathbb{R}$
-linear map
$\mathbb{R}$
-linear map
Proof. Observe that, for
![]() $a \in A_{sa}$
and
$a \in A_{sa}$
and
![]() $u \in U^0(A)$
, we have
$u \in U^0(A)$
, we have
 \begin{equation} \begin{split} e^{2\pi i t S_\theta (uau^*)} &= \theta \left(e^{2\pi i t uau^*}\right) \\ &= \theta \left(ue^{2\pi i t a}u^*\right) \\\ &= \theta (u)e^{2\pi i t S_\theta (a)}\theta (u)^* \\ &= e^{2\pi i t \theta (u)S_\theta (a)\theta (u)^*} \end{split} \end{equation}
\begin{equation} \begin{split} e^{2\pi i t S_\theta (uau^*)} &= \theta \left(e^{2\pi i t uau^*}\right) \\ &= \theta \left(ue^{2\pi i t a}u^*\right) \\\ &= \theta (u)e^{2\pi i t S_\theta (a)}\theta (u)^* \\ &= e^{2\pi i t \theta (u)S_\theta (a)\theta (u)^*} \end{split} \end{equation}
for all
![]() $t \in \mathbb{R}$
. Therefore,
$t \in \mathbb{R}$
. Therefore,
![]() $S_\theta (uau^*) = \theta (u)S_\theta (a)\theta (u)^*$
, and applying
$S_\theta (uau^*) = \theta (u)S_\theta (a)\theta (u)^*$
, and applying
![]() $\tau$
yields
$\tau$
yields
i.e.,
![]() $\tau \circ S_\theta$
is tracial.
$\tau \circ S_\theta$
is tracial.
Thus, if
![]() $a \in A_0$
, it vanishes on every tracial state (hence on every tracial functional), and so
$a \in A_0$
, it vanishes on every tracial state (hence on every tracial functional), and so
![]() $\tau \circ S_\theta (a) = 0$
for all
$\tau \circ S_\theta (a) = 0$
for all
![]() $\tau \in T(B)$
. Therefore,
$\tau \in T(B)$
. Therefore,
![]() $S_\theta (A_0) \subseteq B_0$
and so
$S_\theta (A_0) \subseteq B_0$
and so
![]() $S_\theta$
factors through a map
$S_\theta$
factors through a map
where we identify
![]() $A_{sa}/A_0 \simeq \textrm{Aff}\, T(A)$
and
$A_{sa}/A_0 \simeq \textrm{Aff}\, T(A)$
and
![]() $B_{sa}/B_0 \simeq \textrm{Aff}\, T(B)$
.
$B_{sa}/B_0 \simeq \textrm{Aff}\, T(B)$
.
One cannot expect
![]() $\Lambda _\theta$
(or
$\Lambda _\theta$
(or
![]() $S_\theta$
) to be unital or positive, as the following examples show.
$S_\theta$
) to be unital or positive, as the following examples show.
Example 3.4.
-
1. Consider a continuous homomorphism
 $\theta \,:\, \mathbb{T} \to \mathbb{T} = U^0(\mathbb{C}) = U(\mathbb{C})$
. By Pontryagin duality,
$\theta \,:\, \mathbb{T} \to \mathbb{T} = U^0(\mathbb{C}) = U(\mathbb{C})$
. By Pontryagin duality,
 $\theta (z) = z^n$
for some
$\theta (z) = z^n$
for some
 $n \in \mathbb{Z}$
. We then have that
$n \in \mathbb{Z}$
. We then have that
 $S_\theta \,:\, \mathbb{R} \to \mathbb{R}$
is given by
$S_\theta \,:\, \mathbb{R} \to \mathbb{R}$
is given by
 $S_\theta (x) = nx$
. If
$S_\theta (x) = nx$
. If
 $n \neq 1$
, clearly
$n \neq 1$
, clearly
 $S_\theta$
is not unital. If
$S_\theta$
is not unital. If
 $n \lt 0$
, then
$n \lt 0$
, then
 $S_\theta$
is not positive since it sends
$S_\theta$
is not positive since it sends
 $1$
to
$1$
to
 $n \lt 0$
. An important observation, however, is that if
$n \lt 0$
. An important observation, however, is that if
 $n \lt 0$
,
$n \lt 0$
,
 $-S_\theta \,:\, \mathbb{R} \to \mathbb{R}$
is positive, and
$-S_\theta \,:\, \mathbb{R} \to \mathbb{R}$
is positive, and
 $-\frac{1}{n}S$
is unital and positive.
$-\frac{1}{n}S$
is unital and positive.
-
2. Consider
 $\theta \,:\, \mathbb{T}^3 \to \mathbb{T}$
given by
$\theta \,:\, \mathbb{T}^3 \to \mathbb{T}$
given by
 $\theta (z,w,v) = \overline{z}wv$
. The corresponding map
$\theta (z,w,v) = \overline{z}wv$
. The corresponding map
 $S_\theta \,:\, \mathbb{R}^3 \to \mathbb{R}$
is given by
(3.16)Clearly
$S_\theta \,:\, \mathbb{R}^3 \to \mathbb{R}$
is given by
(3.16)Clearly \begin{equation} S_\theta (a,b,c) = -a + b + c. \end{equation}
\begin{equation} S_\theta (a,b,c) = -a + b + c. \end{equation}
 $(1,0,0) \in \mathbb{C}^3$
is a positive element; however,
$(1,0,0) \in \mathbb{C}^3$
is a positive element; however,
 $S_\theta (1,0,0) = -1 \lt 0$
. This map is, however, unital.
$S_\theta (1,0,0) = -1 \lt 0$
. This map is, however, unital.
-
3. Let
 $\theta \,:\, U_2 \to \mathbb{T}$
be defined by
$\theta \,:\, U_2 \to \mathbb{T}$
be defined by
 $\theta (u) = \det (u)$
. Then
$\theta (u) = \det (u)$
. Then
 $S_\theta \,:\, (M_2)_{sa} \to \mathbb{R}$
is defined by
$S_\theta \,:\, (M_2)_{sa} \to \mathbb{R}$
is defined by
 $S_\theta (A) ={\text{tr}} A$
, where
$S_\theta (A) ={\text{tr}} A$
, where
 $\text{tr}$
is the unnormalized trace. Clearly this map is not unital, but it is positive.
$\text{tr}$
is the unnormalized trace. Clearly this map is not unital, but it is positive.
-
4. Let
 $\theta \,:\, U_2 \to U_3$
be defined by
$\theta \,:\, U_2 \to U_3$
be defined by
 $\theta (u) = u \oplus 1$
. Then
$\theta (u) = u \oplus 1$
. Then
 $S_\theta \,:\, (M_2)_{sa} \to (M_3)_{sa}$
is given by
$S_\theta \,:\, (M_2)_{sa} \to (M_3)_{sa}$
is given by
 $S_\theta (A) = A \oplus 0$
, which is again not unital, but is positive. The induced map
$S_\theta (A) = A \oplus 0$
, which is again not unital, but is positive. The induced map
 $\Lambda _\theta \,:\, \mathbb{R} \to \mathbb{R}$
is given by
$\Lambda _\theta \,:\, \mathbb{R} \to \mathbb{R}$
is given by
 $\Lambda _\theta (x) = \frac{2}{3}x$
for
$\Lambda _\theta (x) = \frac{2}{3}x$
for
 $x \in \mathbb{R}$
.
$x \in \mathbb{R}$
. -
5. Let
 $\theta \,:\, \mathbb{T} \hookrightarrow U_2$
be defined by
(3.17)Then
$\theta \,:\, \mathbb{T} \hookrightarrow U_2$
be defined by
(3.17)Then \begin{equation} \theta (\lambda ) = \begin{pmatrix} \lambda \\ & \lambda \end{pmatrix}. \end{equation}
\begin{equation} \theta (\lambda ) = \begin{pmatrix} \lambda \\ & \lambda \end{pmatrix}. \end{equation}
 $S_\theta$
is a unital, positive isometry and
$S_\theta$
is a unital, positive isometry and
 $\Lambda _\theta$
gives rise the identity map
(3.18)
$\Lambda _\theta$
gives rise the identity map
(3.18) \begin{equation} \mathbb{R} = \textrm{Aff}\, T(\mathbb{C}) \to \textrm{Aff}\, T(M_2) = \mathbb{R}. \end{equation}
\begin{equation} \mathbb{R} = \textrm{Aff}\, T(\mathbb{C}) \to \textrm{Aff}\, T(M_2) = \mathbb{R}. \end{equation}
-
6. Let
 $\theta \,:\, \mathbb{T} \hookrightarrow U_2$
be defined by
(3.19)Then
$\theta \,:\, \mathbb{T} \hookrightarrow U_2$
be defined by
(3.19)Then \begin{equation} \theta (\lambda ) = \begin{pmatrix} \lambda & \\ & \overline{\lambda } \end{pmatrix}. \end{equation}
\begin{equation} \theta (\lambda ) = \begin{pmatrix} \lambda & \\ & \overline{\lambda } \end{pmatrix}. \end{equation}
 $S_\theta \,:\, \mathbb{R} \to (M_2)_{sa}$
is defined by
(3.20)and
$S_\theta \,:\, \mathbb{R} \to (M_2)_{sa}$
is defined by
(3.20)and \begin{equation} S_\theta (x) = \begin{pmatrix} x & \\ & -x \end{pmatrix} \end{equation}
\begin{equation} S_\theta (x) = \begin{pmatrix} x & \\ & -x \end{pmatrix} \end{equation}
 $\Lambda _\theta$
is identically zero.
$\Lambda _\theta$
is identically zero.
The above examples are important. If
![]() $\theta (\mathbb{T}) \subseteq \mathbb{T}$
, which is a moderate assumption (e.g., if
$\theta (\mathbb{T}) \subseteq \mathbb{T}$
, which is a moderate assumption (e.g., if
![]() $\theta$
was the restriction of a unital *-homomorphism or an anti-*-homomorphism), we can restrict the homomorphism to the circle to get a continuous group homomorphism
$\theta$
was the restriction of a unital *-homomorphism or an anti-*-homomorphism), we can restrict the homomorphism to the circle to get a continuous group homomorphism
![]() $\mathbb{T} \to \mathbb{T}$
. We understand such homomorphisms by Pontryagin duality [Reference Folland17, Chapter 4].
$\mathbb{T} \to \mathbb{T}$
. We understand such homomorphisms by Pontryagin duality [Reference Folland17, Chapter 4].
We now use (pre-)determinant techniques in order to show desirable relationships between our maps.
Proposition 3.5.
Let
![]() $A,B$
be unital C*-algebras,
$A,B$
be unital C*-algebras,
![]() $\theta \,:\, U^0(A) \to U^0(B)$
be a uniformly continuous homomorphism,
$\theta \,:\, U^0(A) \to U^0(B)$
be a uniformly continuous homomorphism,
![]() $E$
a real Banach space, and
$E$
a real Banach space, and
![]() $\tau \,:\, B_{sa} \to E$
a bounded trace.
$\tau \,:\, B_{sa} \to E$
a bounded trace.
-
1. Let
 $\xi \,:\, [0,1] \to U^0(A)$
be a piece-wise smooth path with
$\xi \,:\, [0,1] \to U^0(A)$
be a piece-wise smooth path with
 $\xi (0) = 1$
. Then
(3.21)In particular,
$\xi (0) = 1$
. Then
(3.21)In particular, \begin{equation} \tilde{\Delta }_{\tau \circ S_\theta }^1(\xi ) = \tilde{\Delta }_\tau ^1(\theta \circ \xi ). \end{equation}
\begin{equation} \tilde{\Delta }_{\tau \circ S_\theta }^1(\xi ) = \tilde{\Delta }_\tau ^1(\theta \circ \xi ). \end{equation}
 $\tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big) \subseteq \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big)$
.
$\tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big) \subseteq \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big)$
.
-
2. The following diagram commutes:
(3.22)
-
3. The following diagram commutes:
(3.23)
where the map on the right is the canonical map induced from the inclusion
 $\tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big) \subseteq \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big)$
coming from (1). In particular,
$\tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big) \subseteq \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big)$
coming from (1). In particular,
 $\theta \left(\ker \Delta _{\tau \circ S_\theta }^1\right) \subseteq \ker \Delta _\tau ^1$
.
$\theta \left(\ker \Delta _{\tau \circ S_\theta }^1\right) \subseteq \ker \Delta _\tau ^1$
.The analogous diagram commutes if we consider Thomsen’s variant of the de la Harpe–Skandalis determinant associated to
 $\tau$
and
$\tau$
and
 $\tau \circ S_\theta$
in (
3.23
).
$\tau \circ S_\theta$
in (
3.23
).
Proof. By the proof of Proposition 2.2, we can find
![]() $k \in \mathbb{N}$
and
$k \in \mathbb{N}$
and
![]() $a_1,\dots,a_k \in (M_n(A))_{sa}$
such that
$a_1,\dots,a_k \in (M_n(A))_{sa}$
such that
![]() $\xi$
is homotopic to the path
$\xi$
is homotopic to the path
![]() $\eta \,:\, [0,1] \to U(A)$
given by
$\eta \,:\, [0,1] \to U(A)$
given by
and we have that
 \begin{equation} \tilde{\Delta }_\omega ^n(\xi ) = \tilde{\Delta }_\omega ^n(\eta ) = \sum _{j=1}^k \omega (a_j) \end{equation}
\begin{equation} \tilde{\Delta }_\omega ^n(\xi ) = \tilde{\Delta }_\omega ^n(\eta ) = \sum _{j=1}^k \omega (a_j) \end{equation}
whenever
![]() $\omega \,:\, A_{sa} \to F$
is a bounded trace to a real Banach space
$\omega \,:\, A_{sa} \to F$
is a bounded trace to a real Banach space
![]() $F$
.
$F$
.
Now
![]() $\theta \circ \xi$
is homotopic to
$\theta \circ \xi$
is homotopic to
![]() $\theta \circ \eta$
, which has the following form, for
$\theta \circ \eta$
, which has the following form, for
![]() $j=1,\dots,k$
and
$j=1,\dots,k$
and
![]() $t \in \left[\frac{j-1}{k},\frac{j}{k}\right]$
:
$t \in \left[\frac{j-1}{k},\frac{j}{k}\right]$
:
 \begin{equation} \begin{split} \theta \circ \eta (t) &= \theta \circ \xi \left (\frac{j-1}{k}\right )\theta \left (e^{2\pi i (kt - j + 1)a_j}\right ) \\ &= \theta \circ \xi \left (\frac{j-1}{k}\right )e^{2\pi i (kt - j + 1)S_\theta (a_j)}. \end{split} \end{equation}
\begin{equation} \begin{split} \theta \circ \eta (t) &= \theta \circ \xi \left (\frac{j-1}{k}\right )\theta \left (e^{2\pi i (kt - j + 1)a_j}\right ) \\ &= \theta \circ \xi \left (\frac{j-1}{k}\right )e^{2\pi i (kt - j + 1)S_\theta (a_j)}. \end{split} \end{equation}
By taking
![]() $X_j \,:\!=\, \theta \circ \xi \left (\frac{j-1}{k}\right )$
and
$X_j \,:\!=\, \theta \circ \xi \left (\frac{j-1}{k}\right )$
and
![]() $Y_j \,:\!=\, e^{2\pi i (kt - j + 1)S_\theta (a_j)}$
in (2.12), we see that
$Y_j \,:\!=\, e^{2\pi i (kt - j + 1)S_\theta (a_j)}$
in (2.12), we see that
 \begin{equation} \tilde{\Delta }_\tau ^1(\theta \circ \xi ) = \tilde{\Delta }_\tau ^1(\theta \circ \eta ) = \sum _{j=1}^k \tau \left(S_\theta (a_j)\right), \end{equation}
\begin{equation} \tilde{\Delta }_\tau ^1(\theta \circ \xi ) = \tilde{\Delta }_\tau ^1(\theta \circ \eta ) = \sum _{j=1}^k \tau \left(S_\theta (a_j)\right), \end{equation}
and this last quantity is just
![]() $\tilde{\Delta }_{\tau \circ S_\theta }^1(\xi )$
by (3.25).
$\tilde{\Delta }_{\tau \circ S_\theta }^1(\xi )$
by (3.25).
As for parts (2) and (3), they follow from (1). Indeed, (2) is obvious and to see (3) we let
be the canonical surjection. If
![]() $\xi _u\,:\, [0,1] \to U^0(A)$
is a path from 1 to
$\xi _u\,:\, [0,1] \to U^0(A)$
is a path from 1 to
![]() $u$
, then we have that
$u$
, then we have that
 \begin{equation} \begin{split} q\left(\Delta _{\tau \circ S_\theta }^1(u)\right) &= q\left (\tilde{\Delta }_{\tau \circ S_\theta }^1(\xi _u) + \tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big)\right ) \\ &= \tilde{\Delta }_{\tau \circ S_\theta }^1(\xi _u) + \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big) \\ &\overset{(1)}{=} \tilde{\Delta }_\tau ^1(\theta \circ \xi _u) + \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big) \\ &= \Delta _\tau ^1(\theta (u)). \end{split} \end{equation}
\begin{equation} \begin{split} q\left(\Delta _{\tau \circ S_\theta }^1(u)\right) &= q\left (\tilde{\Delta }_{\tau \circ S_\theta }^1(\xi _u) + \tilde{\Delta }_{\tau \circ S_\theta }^1\big(\pi _1\big(U^0(A)\big)\big)\right ) \\ &= \tilde{\Delta }_{\tau \circ S_\theta }^1(\xi _u) + \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big) \\ &\overset{(1)}{=} \tilde{\Delta }_\tau ^1(\theta \circ \xi _u) + \tilde{\Delta }_\tau ^1\big(\pi _1\big(U^0(B)\big)\big) \\ &= \Delta _\tau ^1(\theta (u)). \end{split} \end{equation}
The remark about Thomsen’s variant is obvious.
Corollary 3.6. The following diagram commutes:

In particular, when the canonical maps
are isomorphisms, we have that

commutes, where
![]() $K_0(\theta )\,:\, K_0(A) \to K_0(B)$
is the map induced from the diagram
$K_0(\theta )\,:\, K_0(A) \to K_0(B)$
is the map induced from the diagram

Proof. By definition, we have that
![]() $\Lambda _\theta \circ \text{Tr}_A = S_\theta \circ \text{Tr}_B$
and so if
$\Lambda _\theta \circ \text{Tr}_A = S_\theta \circ \text{Tr}_B$
and so if
![]() $\xi \,:\, [0,1] \to U^0(A)$
is a (piece-wise smooth) path, we haveFootnote
3
$\xi \,:\, [0,1] \to U^0(A)$
is a (piece-wise smooth) path, we haveFootnote
3
 \begin{align} \Lambda _\theta \left (\tilde{\Delta }_{\text{Tr}_A}^1(\xi )\right ) &= \Lambda _\theta \left (\int _0^1 \text{Tr}_A\left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt\right ) \nonumber\\ &= \int _0^1 \Lambda _\theta \circ \text{Tr}_A\left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt\ \nonumber\\ &= \int _0^1 \text{Tr}_B \circ S_\theta \left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt \\ &= \tilde{\Delta }_{\text{Tr}_B \circ S_\theta }(\xi ).\nonumber \end{align}
\begin{align} \Lambda _\theta \left (\tilde{\Delta }_{\text{Tr}_A}^1(\xi )\right ) &= \Lambda _\theta \left (\int _0^1 \text{Tr}_A\left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt\right ) \nonumber\\ &= \int _0^1 \Lambda _\theta \circ \text{Tr}_A\left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt\ \nonumber\\ &= \int _0^1 \text{Tr}_B \circ S_\theta \left (\xi^{\prime}(t)\xi (t)^{-1}\right )dt \\ &= \tilde{\Delta }_{\text{Tr}_B \circ S_\theta }(\xi ).\nonumber \end{align}
Now we note that the diagram

commutes, where the top triangle commutes by the (3.34) and the bottom square commutes by Proposition 3.5(2). This gives that (3.30) commutes.
The second part follows since if
![]() $\xi$
is a (piece-wise smooth) path in
$\xi$
is a (piece-wise smooth) path in
![]() $U_n(A)$
and
$U_n(A)$
and
![]() $m \gt n$
, then
$m \gt n$
, then
Proposition 3.7.
Let
![]() $A,B$
be unital C*-algebras. Then the map
$A,B$
be unital C*-algebras. Then the map
![]() $\Lambda _\theta$
is a lift of the map
$\Lambda _\theta$
is a lift of the map
as described in ( 3.4 ).
Proof. Let us label the maps in the diagram (3.4):

where
![]() $\tilde \theta ([u]) \,:\!=\, [\theta (u)]$
,
$\tilde \theta ([u]) \,:\!=\, [\theta (u)]$
,
![]() $\delta _A^1\big(\big[e^{2\pi i a}\big]\big) \,:\!=\, [\hat{a}]$
,
$\delta _A^1\big(\big[e^{2\pi i a}\big]\big) \,:\!=\, [\hat{a}]$
,
![]() $\delta _B^1$
is defined similarly, and
$\delta _B^1$
is defined similarly, and
But then we have that
 \begin{equation} \begin{split} P([a]) &= \delta _B^1 \circ \tilde \theta \circ \left(\delta _A^1\right)^{-1}([\hat{a}]) \\ &= \delta _B^1 \circ \tilde \theta \left(\left[e^{2\pi i a}\right]\right) \\ &= \delta _B^1\left(\left[\theta \left(e^{2\pi i a}\right)\right]\right) \\ &= \delta _B^1\left(\left[e^{2\pi i S_\theta (a)}\right]\right) \\ &= \left[\widehat{S_\theta (a)}\right] \\ &= \left[\Lambda _\theta (\widehat{a})\right] \end{split} \end{equation}
\begin{equation} \begin{split} P([a]) &= \delta _B^1 \circ \tilde \theta \circ \left(\delta _A^1\right)^{-1}([\hat{a}]) \\ &= \delta _B^1 \circ \tilde \theta \left(\left[e^{2\pi i a}\right]\right) \\ &= \delta _B^1\left(\left[\theta \left(e^{2\pi i a}\right)\right]\right) \\ &= \delta _B^1\left(\left[e^{2\pi i S_\theta (a)}\right]\right) \\ &= \left[\widehat{S_\theta (a)}\right] \\ &= \left[\Lambda _\theta (\widehat{a})\right] \end{split} \end{equation}
In particular, the diagram

commutes, where
![]() $q_A^1$
and
$q_A^1$
and
![]() $q_B^1$
are the respective quotient maps.
$q_B^1$
are the respective quotient maps.
Proposition 3.8.
Let
![]() $A,B$
be unital C*-algebras and
$A,B$
be unital C*-algebras and
![]() $\theta : U^0(A) \to U^0(B)$
be a continuous group homomorphism. Then,
$\theta : U^0(A) \to U^0(B)$
be a continuous group homomorphism. Then,
![]() $\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a lift of the map
$\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a lift of the map
as described in ( 3.2 ).
Proof. One can mimic the proof above or apply the above result and appeal to the commuting diagram

where the vertical maps are defined via the diagrams from (3.4) and (3.2), respectively, and the horizontal maps are the canonical surjections.
In particular, assuming some
![]() $K_0$
-regularity gives that
$K_0$
-regularity gives that
![]() $\Lambda _\theta$
is a lift of a map between quotients of spaces of continuous real-valued affine functions by images of
$\Lambda _\theta$
is a lift of a map between quotients of spaces of continuous real-valued affine functions by images of
![]() $K_0$
.
$K_0$
.
Corollary 3.9.
Let
![]() $A,B$
be unital C*-algebras such that the canonical maps
$A,B$
be unital C*-algebras such that the canonical maps
are surjections. If
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous homomorphism, then
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous homomorphism, then
![]() $\Lambda _\theta$
is a lift of the maps on the right of the following two commutative diagrams:
$\Lambda _\theta$
is a lift of the maps on the right of the following two commutative diagrams:

and

Further, if
![]() $\ker \Delta _A^1 = DU^0(A)$
and
$\ker \Delta _A^1 = DU^0(A)$
and
![]() $\ker \Delta _B^1 = DU^0(B)$
, then
$\ker \Delta _B^1 = DU^0(B)$
, then
![]() $\Lambda _\theta$
is a lift of the map induced by the diagram
$\Lambda _\theta$
is a lift of the map induced by the diagram

C*-algebras satisfying the last condition arise naturally—for example, unital, separable, simple, pure C*-algebras of stable rank 1 such that every 2-quasitracial state on
![]() $A$
is a trace have this property [Reference Ng and Robert27].
$A$
is a trace have this property [Reference Ng and Robert27].
4. The order on
 $\textbf{Aff}\, \boldsymbol{T}(\cdot )$
$\textbf{Aff}\, \boldsymbol{T}(\cdot )$
We now examine when the map induced on
![]() $\textrm{Aff}\, T(\cdot )$
is positive in order to compare
$\textrm{Aff}\, T(\cdot )$
is positive in order to compare
![]() $K$
-theory, traces, and the pairing. As we saw in Example 3.4, the map we get between spaces of affine functions on the trace simplices need not be positive nor unital in general. In this section, we will be able to use the map
$K$
-theory, traces, and the pairing. As we saw in Example 3.4, the map we get between spaces of affine functions on the trace simplices need not be positive nor unital in general. In this section, we will be able to use the map
![]() $\Lambda _\theta$
to construct a unital positive map, under some extra assumptions on
$\Lambda _\theta$
to construct a unital positive map, under some extra assumptions on
![]() $\theta$
.
$\theta$
.
We record the following results as they give us necessary and sufficient conditions for the
![]() $\Lambda _\theta$
to be positive. We use the C*-algebra-valued analog of the fact that any unital, contractive linear functional is positive, along with the fact that completely positive maps are (completely) bounded with the norm determined by the image of the unit. Recall that an operator system is a self-adjoint unital subspace of a C*-algebra. The following is a combination of Proposition 2.11, Theorem 3.9, and Proposition 3.6 in [Reference Paulsen29].
$\Lambda _\theta$
to be positive. We use the C*-algebra-valued analog of the fact that any unital, contractive linear functional is positive, along with the fact that completely positive maps are (completely) bounded with the norm determined by the image of the unit. Recall that an operator system is a self-adjoint unital subspace of a C*-algebra. The following is a combination of Proposition 2.11, Theorem 3.9, and Proposition 3.6 in [Reference Paulsen29].
Proposition 4.1.
Let
![]() $\mathcal{S}$
be an operator system and
$\mathcal{S}$
be an operator system and
![]() $B$
a unital C*-algebra.
$B$
a unital C*-algebra.
-
1. If
 $\phi \,:\, \mathcal{S} \to B$
is a unital contraction, then
$\phi \,:\, \mathcal{S} \to B$
is a unital contraction, then
 $\phi$
is positive.
$\phi$
is positive.
-
2. If
 $B = C(X)$
and
$B = C(X)$
and
 $\phi \,:\, \mathcal{S} \to B$
is positive, then it is bounded with
$\phi \,:\, \mathcal{S} \to B$
is positive, then it is bounded with
 $\|\phi \| = \|\phi (1)\|$
.
$\|\phi \| = \|\phi (1)\|$
.
Lemma 4.2.
Suppose
![]() $A,B$
are unital C*-algebras and
$A,B$
are unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism such that
$\theta \,:\, U^0(A) \to U^0(B)$
be a continuous group homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. If
$\theta (\mathbb{T}) = \mathbb{T}$
. If
![]() $\theta |_{\mathbb{T}}$
is injective, then
$\theta |_{\mathbb{T}}$
is injective, then
![]() $S_\theta (1) \in \{1,-1\}$
.
$S_\theta (1) \in \{1,-1\}$
.
Proof. The restriction
![]() $\theta |_{\mathbb{T}}\,:\, \mathbb{T} \to \mathbb{T}$
is a continuous group homomorphism, hence by Pontryagin duality is of the form
$\theta |_{\mathbb{T}}\,:\, \mathbb{T} \to \mathbb{T}$
is a continuous group homomorphism, hence by Pontryagin duality is of the form
![]() $\theta (z) = z^n$
for some
$\theta (z) = z^n$
for some
![]() $n$
. Injectivity implies that
$n$
. Injectivity implies that
![]() $n \in \{1,-1\}$
. We then have that
$n \in \{1,-1\}$
. We then have that
for all
![]() $t \in \mathbb{R}$
. This implies that
$t \in \mathbb{R}$
. This implies that
![]() $S_\theta (1) = n\cdot 1 \in \{1,-1\}$
.
$S_\theta (1) = n\cdot 1 \in \{1,-1\}$
.
In the sequel, we will be interested in the case that
![]() $T(A) \neq \emptyset$
. The map
$T(A) \neq \emptyset$
. The map
![]() $S_\theta$
will still descend to a map
$S_\theta$
will still descend to a map
![]() $\Lambda _\theta \,:\, A_{sa}/A_0 \to B_{sa}/B_0$
regardless of their being tracial states on either C*-algebra, but these quotients are zero if there are no traces. If we take the zero Banach space to be partially ordered with order unit trivially, then one can speak of unital and positive maps
$\Lambda _\theta \,:\, A_{sa}/A_0 \to B_{sa}/B_0$
regardless of their being tracial states on either C*-algebra, but these quotients are zero if there are no traces. If we take the zero Banach space to be partially ordered with order unit trivially, then one can speak of unital and positive maps
![]() $\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
, regardless of whether
$\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
, regardless of whether
![]() $T(B)$
is empty or not (any map from a partially ordered Banach space with order unit to the zero Banach space will be unital and positive). However, if
$T(B)$
is empty or not (any map from a partially ordered Banach space with order unit to the zero Banach space will be unital and positive). However, if
![]() $T(A) = \emptyset$
and
$T(A) = \emptyset$
and
![]() $T(B) \neq \emptyset$
, then our map
$T(B) \neq \emptyset$
, then our map
![]() $\Lambda _\theta$
would have no chance of being unital. We identify the zero Banach space with
$\Lambda _\theta$
would have no chance of being unital. We identify the zero Banach space with
![]() $\textrm{Aff}\, (\emptyset ) = C_{\mathbb{R}}(\emptyset )$
and with the complex analogs as well. However, the following lemma is true regardless of whether
$\textrm{Aff}\, (\emptyset ) = C_{\mathbb{R}}(\emptyset )$
and with the complex analogs as well. However, the following lemma is true regardless of whether
![]() $T(A)$
is empty or not.
$T(A)$
is empty or not.
Lemma 4.3.
Suppose
![]() $A,B$
are unital C*-algebras and
$A,B$
are unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism such that
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. If
$\theta (\mathbb{T}) = \mathbb{T}$
. If
![]() $\theta$
is injective, the following are equivalent:
$\theta$
is injective, the following are equivalent:
-
1. one of
 $\Lambda _\theta$
or
$\Lambda _\theta$
or
 $-\Lambda _\theta$
is positive;
$-\Lambda _\theta$
is positive;
-
2.
 $\Lambda _\theta$
is contractive.
$\Lambda _\theta$
is contractive.
Proof. First suppose that
![]() $T(A),T(B) \neq \emptyset$
. By Lemma 4.2, we know that
$T(A),T(B) \neq \emptyset$
. By Lemma 4.2, we know that
![]() $S_\theta (1) \in \{1,-1\}$
and consequently
$S_\theta (1) \in \{1,-1\}$
and consequently
![]() $\Lambda _\theta (\hat 1) \in \{\hat{1},\widehat{-1}\}$
(where we recall that, for
$\Lambda _\theta (\hat 1) \in \{\hat{1},\widehat{-1}\}$
(where we recall that, for
![]() $a \in A_{sa}$
,
$a \in A_{sa}$
,
![]() $\hat{a} \in \textrm{Aff}\, T(A)$
is the affine function
$\hat{a} \in \textrm{Aff}\, T(A)$
is the affine function
![]() $\hat{a}(\tau ) = \tau (a)$
). By replacing
$\hat{a}(\tau ) = \tau (a)$
). By replacing
![]() $\Lambda _\theta$
with
$\Lambda _\theta$
with
![]() $-\Lambda _\theta$
, we can without loss of generality assume that
$-\Lambda _\theta$
, we can without loss of generality assume that
![]() $\Lambda _\theta$
is unital. Using the fact that
$\Lambda _\theta$
is unital. Using the fact that
![]() $\textrm{Aff}\, T(A) + i\textrm{Aff}\, T(A) \subseteq C(T(A))$
is an operator system and the canonical extension
$\textrm{Aff}\, T(A) + i\textrm{Aff}\, T(A) \subseteq C(T(A))$
is an operator system and the canonical extension
is a unital linear map with abelian target algebra, this is an easy consequence of the two parts of Proposition 4.1.
Finally, if
![]() $T(A) = \emptyset$
, then any map from
$T(A) = \emptyset$
, then any map from
![]() $\textrm{Aff}\, T(A)$
is both contractive and positive trivially. The same is true of any map with codomain
$\textrm{Aff}\, T(A)$
is both contractive and positive trivially. The same is true of any map with codomain
![]() $\textrm{Aff}\, T(B)$
if
$\textrm{Aff}\, T(B)$
if
![]() $T(B) = \emptyset$
.
$T(B) = \emptyset$
.
Lemma 4.4.
Suppose
![]() $A,B$
are unital C*-algebras and
$A,B$
are unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism. Suppose that
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism. Suppose that
![]() $T(A) \neq \emptyset$
.
$T(A) \neq \emptyset$
.
-
1.
 $\|\Lambda _\theta \| \leq \|S_\theta \|$
.
$\|\Lambda _\theta \| \leq \|S_\theta \|$
. -
2. If
 $K \gt 0$
is such that
$K \gt 0$
is such that
 $\|\theta (u) - \theta (v)\| \leq K\|u - v\|$
for all
$\|\theta (u) - \theta (v)\| \leq K\|u - v\|$
for all
 $u,v \in U^0(A)$
, then
$u,v \in U^0(A)$
, then
 $\|S_\theta \| \leq K$
and
$\|S_\theta \| \leq K$
and
 $\|\Lambda _\theta \| \leq K$
.
$\|\Lambda _\theta \| \leq K$
. -
3. If
 $\theta$
is a homeomorphism, then
$\theta$
is a homeomorphism, then
 $\Lambda _\theta$
is bijective with bounded inverse being
$\Lambda _\theta$
is bijective with bounded inverse being
 $\Lambda _{\theta ^{-1}}$
.
$\Lambda _{\theta ^{-1}}$
. -
4. If
 $\theta$
is isometric, then so is
$\theta$
is isometric, then so is
 $S_\theta$
. If
$S_\theta$
. If
 $\theta$
is a surjective isometry, then
$\theta$
is a surjective isometry, then
 $\Lambda _\theta$
is a surjective isometry.
$\Lambda _\theta$
is a surjective isometry.
Proof. As
![]() $S_\theta (A_0) \subseteq B_0$
, we have
$S_\theta (A_0) \subseteq B_0$
, we have
 \begin{equation} \begin{split} \|\Lambda _\theta (\hat{a})\|_{\textrm{Aff}\, T(B)} &= \|\widehat{S_\theta (a)}\|_{\textrm{Aff}\, T(B)} \\ &= \inf _{b \in B_0} \|S_\theta (a) + b\| \\ &\leq \inf _{b \in \theta (A_0)} \|S_\theta (a) + b\| \\ &= \inf _{a^{\prime} \in A_0} \|S_\theta (a) + S_\theta (a^{\prime})\| \\ &\leq \|S_\theta \|\inf _{a^{\prime} \in A_0}\|a + a^{\prime}\| \\ &= \|S_\theta \|\|\hat{a}\|_{\textrm{Aff}\, T(A)} \end{split} \end{equation}
\begin{equation} \begin{split} \|\Lambda _\theta (\hat{a})\|_{\textrm{Aff}\, T(B)} &= \|\widehat{S_\theta (a)}\|_{\textrm{Aff}\, T(B)} \\ &= \inf _{b \in B_0} \|S_\theta (a) + b\| \\ &\leq \inf _{b \in \theta (A_0)} \|S_\theta (a) + b\| \\ &= \inf _{a^{\prime} \in A_0} \|S_\theta (a) + S_\theta (a^{\prime})\| \\ &\leq \|S_\theta \|\inf _{a^{\prime} \in A_0}\|a + a^{\prime}\| \\ &= \|S_\theta \|\|\hat{a}\|_{\textrm{Aff}\, T(A)} \end{split} \end{equation}
whenever
![]() $a \in A_{sa}$
. This gives that
$a \in A_{sa}$
. This gives that
![]() $\|\Lambda _\theta \| \leq \|S_\theta \|$
.
$\|\Lambda _\theta \| \leq \|S_\theta \|$
.
The fact that
![]() $S_\theta$
is an isometry whenever
$S_\theta$
is an isometry whenever
![]() $\theta$
is an isometry follows from an argument in [Reference Hatori and Molnár24]; we exemplify said argument to show the bound condition. We use the observation that
$\theta$
is an isometry follows from an argument in [Reference Hatori and Molnár24]; we exemplify said argument to show the bound condition. We use the observation that
as
![]() $t \to 0$
. Since
$t \to 0$
. Since
for all
![]() $t \in \mathbb{R}$
, we can divide both sides by
$t \in \mathbb{R}$
, we can divide both sides by
![]() $\frac{1}{2\pi }|t|$
and take
$\frac{1}{2\pi }|t|$
and take
![]() $t \to 0$
to get that
$t \to 0$
to get that
Thus,
![]() $\|S_\theta \| \leq K$
. It then follows from (1) that
$\|S_\theta \| \leq K$
. It then follows from (1) that
![]() $\|\Lambda _\theta \| \leq K$
as well.
$\|\Lambda _\theta \| \leq K$
as well.
If
![]() $\theta$
is a homeomorphism,
$\theta$
is a homeomorphism,
![]() $S_\theta$
and
$S_\theta$
and
![]() $S_{\theta ^{-1}}$
are both defined and its clear that
$S_{\theta ^{-1}}$
are both defined and its clear that
![]() $S_\theta ^{-1} = S_{\theta ^{-1}}$
.
$S_\theta ^{-1} = S_{\theta ^{-1}}$
.
The surjectivity of
![]() $\theta$
implies the surjectivity of
$\theta$
implies the surjectivity of
![]() $S_\theta$
and thus if
$S_\theta$
and thus if
![]() $b \in B_{sa}$
, we can find
$b \in B_{sa}$
, we can find
![]() $a \in A_{sa}$
with
$a \in A_{sa}$
with
![]() $S_\theta (a) = b$
. But then
$S_\theta (a) = b$
. But then
![]() $\Lambda _\theta (\hat{a}) = \widehat{S_\theta (a)} = \hat{b}$
. In particular,
$\Lambda _\theta (\hat{a}) = \widehat{S_\theta (a)} = \hat{b}$
. In particular,
![]() $\Lambda _\theta$
is surjective. Now if
$\Lambda _\theta$
is surjective. Now if
![]() $\theta$
is a surjective isometry, we identify
$\theta$
is a surjective isometry, we identify
![]() $\textrm{Aff}\, T(A) \simeq A_{sa}/A_0$
and
$\textrm{Aff}\, T(A) \simeq A_{sa}/A_0$
and
![]() $\textrm{Aff}\, T(B) \simeq B_{sa}/B_0$
, noting that
$\textrm{Aff}\, T(B) \simeq B_{sa}/B_0$
, noting that
![]() $S_\theta (A_0) = B_0$
, and that
$S_\theta (A_0) = B_0$
, and that
![]() $\Lambda _\theta$
will preserve the quotient norms.
$\Lambda _\theta$
will preserve the quotient norms.
Corollary 4.5.
Suppose
![]() $A,B$
are unital C*-algebras and
$A,B$
are unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism. Suppose that
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous group homomorphism. Suppose that
![]() $T(A) \neq \emptyset$
. If
$T(A) \neq \emptyset$
. If
![]() $S_\theta (1) = n$
and
$S_\theta (1) = n$
and
![]() $\|S_\theta \| = |n|$
, then
$\|S_\theta \| = |n|$
, then
![]() $\frac{1}{n}S_\theta$
is a unital contraction, hence positive. In particular, if
$\frac{1}{n}S_\theta$
is a unital contraction, hence positive. In particular, if
![]() $\theta (\mathbb{T}) = \mathbb{T}$
and
$\theta (\mathbb{T}) = \mathbb{T}$
and
![]() $\theta |_{\mathbb{T}}$
is an injection, then either
$\theta |_{\mathbb{T}}$
is an injection, then either
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
is unital and positive.
$-\Lambda _\theta$
is unital and positive.
Proof. The first part follows from the above lemma. If
![]() $\theta$
is an injection with
$\theta$
is an injection with
![]() $\theta (\mathbb{T}) = \mathbb{T}$
, we have that
$\theta (\mathbb{T}) = \mathbb{T}$
, we have that
![]() $S_\theta (\hat{1}) \in \{\hat{1},\widehat{-1}\}$
and that
$S_\theta (\hat{1}) \in \{\hat{1},\widehat{-1}\}$
and that
![]() $\Lambda _\theta$
is contractive, so one of
$\Lambda _\theta$
is contractive, so one of
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
is a unital contraction, hence positive by part (1) of Proposition 4.1.
$-\Lambda _\theta$
is a unital contraction, hence positive by part (1) of Proposition 4.1.
Theorem 4.6.
Suppose
![]() $A,B$
are unital C*-algebras and
$A,B$
are unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a contractive injective homomorphism such that
$\theta \,:\, U^0(A) \to U^0(B)$
is a contractive injective homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
$\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
![]() $T(A) \neq \emptyset$
. Then there is a continuous affine map
$T(A) \neq \emptyset$
. Then there is a continuous affine map
![]() $T_\theta \,:\, T(B) \to T(A)$
such that
$T_\theta \,:\, T(B) \to T(A)$
such that
![]() $\Lambda _\theta (f) = f \circ T_\theta$
or
$\Lambda _\theta (f) = f \circ T_\theta$
or
![]() $-\Lambda _\theta (f) = f \circ T_\theta$
, depending on whether
$-\Lambda _\theta (f) = f \circ T_\theta$
, depending on whether
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
is positive.
$-\Lambda _\theta$
is positive.
Proof. This follows from the fact that the induced map
![]() $\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
will have the property that
$\Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
will have the property that
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
will be a unital positive map. Therefore, by contravariant identification of compact convex sets (of locally convex Hausdorff linear spaces) with the state space of the space of continuous real-valued affine valued functions on them [Reference Goodearl21, Chapter 7], there exists a continuous affine map
$-\Lambda _\theta$
will be a unital positive map. Therefore, by contravariant identification of compact convex sets (of locally convex Hausdorff linear spaces) with the state space of the space of continuous real-valued affine valued functions on them [Reference Goodearl21, Chapter 7], there exists a continuous affine map
![]() $T_\theta \,:\, T(B) \to T(A)$
.
$T_\theta \,:\, T(B) \to T(A)$
.
Theorem 4.7.
Suppose
![]() $A,B$
be unital C*-algebras and
$A,B$
be unital C*-algebras and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a contractive topological group isomorphism such that
$\theta \,:\, U^0(A) \to U^0(B)$
is a contractive topological group isomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
$\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
![]() $T(A) \neq \emptyset$
. Then the map
$T(A) \neq \emptyset$
. Then the map
![]() $T_\theta \,:\, T(B) \to T(A)$
induced by
$T_\theta \,:\, T(B) \to T(A)$
induced by
![]() $\Lambda _\theta$
is an affine homeomorphism.
$\Lambda _\theta$
is an affine homeomorphism.
Proof. As
![]() $\theta (\mathbb{T}) = \mathbb{T}$
,
$\theta (\mathbb{T}) = \mathbb{T}$
,
![]() $S_\theta (1) \in \{-1,1\}$
. Let
$S_\theta (1) \in \{-1,1\}$
. Let
![]() $\pm \Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
be either
$\pm \Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
be either
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
, depending on which is unital, positive, contractive and surjective by combining Lemmas 4.4, 4.3 and 3.2(2). By the duality of (compact) simplices and continuous affine functions on them, the map
$-\Lambda _\theta$
, depending on which is unital, positive, contractive and surjective by combining Lemmas 4.4, 4.3 and 3.2(2). By the duality of (compact) simplices and continuous affine functions on them, the map
![]() $T_\theta \,:\, T(B) \to T(A)$
is an affine homeomorphism.
$T_\theta \,:\, T(B) \to T(A)$
is an affine homeomorphism.
Theorem 4.8.
Let
![]() $A,B$
be unital C*-algebras and
$A,B$
be unital C*-algebras and
![]() $\theta \,:\, U(A) \to U(B)$
be a contractive injective homomorphism such that
$\theta \,:\, U(A) \to U(B)$
be a contractive injective homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
$\theta (\mathbb{T}) = \mathbb{T}$
. Suppose that
![]() $T(A) \neq \emptyset$
. If
$T(A) \neq \emptyset$
. If
Footnote 4 via the canonical maps, then there is an induced map
Proof. Let
-
 $\Lambda \,:\!=\, \Lambda _{\theta |_{U^0(A)}}\,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
,
$\Lambda \,:\!=\, \Lambda _{\theta |_{U^0(A)}}\,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
, -
 $\theta _0\,:\, \pi _1\big(U^0(A)\big) \to \pi _1\big(U^0(B)\big)$
be the map induced on fundamental groups by
$\theta _0\,:\, \pi _1\big(U^0(A)\big) \to \pi _1\big(U^0(B)\big)$
be the map induced on fundamental groups by
 $\theta |_{U^0(A)}$
,
$\theta |_{U^0(A)}$
, -
 $K_0(\theta )$
be the map induced on
$K_0(\theta )$
be the map induced on
 $K_0$
by
$K_0$
by
 $\theta _0$
together with (4.7) for
$\theta _0$
together with (4.7) for
 $i = 1$
,
$i = 1$
, -
 $\theta _1\,:\, \pi _0(U(A)) \to \pi _0(U(B))$
be the map induced by
$\theta _1\,:\, \pi _0(U(A)) \to \pi _0(U(B))$
be the map induced by
 $\theta$
on connected components (so that
$\theta$
on connected components (so that
 $\theta _1([u]_{\sim _h}) = [\theta _1(u)]_{\sim _h}$
) and
$\theta _1([u]_{\sim _h}) = [\theta _1(u)]_{\sim _h}$
) and -
 $K_1(\theta )$
be the map induced by
$K_1(\theta )$
be the map induced by
 $\theta _1$
together with (4.7) for
$\theta _1$
together with (4.7) for
 $i=0$
.
$i=0$
.
Then
is a
![]() $KT_u$
-morphism, where
$KT_u$
-morphism, where
![]() $\pm \Lambda$
is either
$\pm \Lambda$
is either
![]() $\Lambda$
or
$\Lambda$
or
![]() $-\Lambda$
depending on which one is unital and positive, and
$-\Lambda$
depending on which one is unital and positive, and
![]() $\pm K_0(\theta )$
is either
$\pm K_0(\theta )$
is either
![]() $K_0(\theta )$
if
$K_0(\theta )$
if
![]() $\Lambda$
is positive or
$\Lambda$
is positive or
![]() $-K_0(\theta )$
if
$-K_0(\theta )$
if
![]() $-\Lambda$
is positive. Indeed,
$-\Lambda$
is positive. Indeed,
![]() $\pm K_0(\theta ),\theta _1,\pm \Lambda$
are all appropriate morphisms, and we have that
$\pm K_0(\theta ),\theta _1,\pm \Lambda$
are all appropriate morphisms, and we have that

commutesFootnote 5 by Corollary 3.6.
Corollary 4.9.
Let
![]() $A,B$
be unital C*-algebras,
$A,B$
be unital C*-algebras,
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a contractive topological group isomorphism such that
$\theta \,:\, U^0(A) \to U^0(B)$
is a contractive topological group isomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
, and suppose that
$\theta (\mathbb{T}) = \mathbb{T}$
, and suppose that
![]() $T(A) \neq \emptyset$
. If
$T(A) \neq \emptyset$
. If
via the canonical maps, then
![]() $KT_u(A) \simeq KT_u(B)$
.
$KT_u(A) \simeq KT_u(B)$
.
Proof. By Corollary 4.8, we have an induced
![]() $KT_u$
-morphism. This map is necessarily an isomorphism since
$KT_u$
-morphism. This map is necessarily an isomorphism since
![]() $\theta$
is.
$\theta$
is.
Corollary 4.10.
Let
![]() $A,B$
be unital C*-algebras which are either
$A,B$
be unital C*-algebras which are either
![]() $\mathcal{Z}$
-stable or of stable rank one and suppose that
$\mathcal{Z}$
-stable or of stable rank one and suppose that
![]() $T(A) \neq \emptyset$
. Let
$T(A) \neq \emptyset$
. Let
![]() $\theta \,:\, U(A) \to U(B)$
be a contractive injective homomorphism such that
$\theta \,:\, U(A) \to U(B)$
be a contractive injective homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
. Then there is an induced map
$\theta (\mathbb{T}) = \mathbb{T}$
. Then there is an induced map
Proof. C*-algebras which are
![]() $\mathcal{Z}$
-stable or have stable rank one satisfy the hypotheses of Theorem 4.8 by [Reference Jiang25] and [Reference Rieffel32], respectively. So Theorem 4.8 applies.
$\mathcal{Z}$
-stable or have stable rank one satisfy the hypotheses of Theorem 4.8 by [Reference Jiang25] and [Reference Rieffel32], respectively. So Theorem 4.8 applies.
Remark 4.11.
The strict ordering on
![]() $\textrm{Aff}\, T(A)$
is given by
$\textrm{Aff}\, T(A)$
is given by
![]() $f \gg g$
if
$f \gg g$
if
![]() $f(\tau ) \gt g(\tau )$
for all
$f(\tau ) \gt g(\tau )$
for all
![]() $\tau \in T(A)$
. If
$\tau \in T(A)$
. If
![]() $A,B$
are unital with
$A,B$
are unital with
![]() $T(A) \neq \emptyset$
and
$T(A) \neq \emptyset$
and
![]() $\theta \,:\,U^0(A) \to U^0(B)$
is a contractive injective homomorphism such that
$\theta \,:\,U^0(A) \to U^0(B)$
is a contractive injective homomorphism such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
, then
$\theta (\mathbb{T}) = \mathbb{T}$
, then
![]() $\pm \Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a unital positive contraction by Lemma 4.3 (again
$\pm \Lambda _\theta \,:\, \textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
is a unital positive contraction by Lemma 4.3 (again
![]() $\pm \Lambda _\theta$
is
$\pm \Lambda _\theta$
is
![]() $\Lambda _\theta$
or
$\Lambda _\theta$
or
![]() $-\Lambda _\theta$
depending on which is positive). We moreover have that
$-\Lambda _\theta$
depending on which is positive). We moreover have that
Indeed, let us show that
![]() $f \gg 0$
if and only if its image is
$f \gg 0$
if and only if its image is
![]() $\gg 0$
. As
$\gg 0$
. As
![]() $\pm \Lambda _\theta$
has the form
$\pm \Lambda _\theta$
has the form
![]() $\pm \Lambda _\theta (\hat{a}) = \widehat{\pm S_\theta (a)}$
, it suffices to show that if
$\pm \Lambda _\theta (\hat{a}) = \widehat{\pm S_\theta (a)}$
, it suffices to show that if
![]() $\sigma (a) \gt 0$
for all
$\sigma (a) \gt 0$
for all
![]() $\sigma \in T(A)$
, then
$\sigma \in T(A)$
, then
![]() $\tau (\pm S_\theta (a)) \gt 0$
for all
$\tau (\pm S_\theta (a)) \gt 0$
for all
![]() $\tau \in T(B)$
. But this is trivial because
$\tau \in T(B)$
. But this is trivial because
![]() $\tau \circ \pm S_{\theta }\,:\, A_{sa} \to \mathbb{R}$
extends canonically to a tracial state
$\tau \circ \pm S_{\theta }\,:\, A_{sa} \to \mathbb{R}$
extends canonically to a tracial state
![]() $A \to \mathbb{C}$
by Proposition 3.3
, so evaluating it against
$A \to \mathbb{C}$
by Proposition 3.3
, so evaluating it against
![]() $a$
must give that it is strictly positive.
$a$
must give that it is strictly positive.
The above says the following: for certain C*-algebras, we can read off positivity in
![]() $K_0$
, thinking of it as the fundamental group of the unitary group, from the strict positivity of the predeterminant applied a the loop. Precisely, a nonzero element
$K_0$
, thinking of it as the fundamental group of the unitary group, from the strict positivity of the predeterminant applied a the loop. Precisely, a nonzero element
![]() $x \in K_0(A)$
, where
$x \in K_0(A)$
, where
![]() $A$
is a unital, simple C*-algebra with strict comparison, is in the positive cone if and only if the corresponding loop
$A$
is a unital, simple C*-algebra with strict comparison, is in the positive cone if and only if the corresponding loop
![]() $\xi _x$
satisfies
$\xi _x$
satisfies
![]() $\tilde{\Delta }_\tau (\xi _x) \gt 0$
for all
$\tilde{\Delta }_\tau (\xi _x) \gt 0$
for all
![]() $\tau \in T(A)$
.
$\tau \in T(A)$
.
Although the following is known, for example, by very strong results in [Reference Ara and Mathieu1, Chapter 6] pertaining to certain prime C*-algebras, we give the following as a corollary by using
![]() $K$
-theoretic classification results.
$K$
-theoretic classification results.
Corollary 4.12.
Let
![]() $A,B$
be unital, separable, simple, nuclear
$A,B$
be unital, separable, simple, nuclear
![]() $\mathcal{Z}$
-stable C*-algebras satisfying the UCT. Then
$\mathcal{Z}$
-stable C*-algebras satisfying the UCT. Then
![]() $A \simeq B$
if and only if there is a contractive isomorphism
$A \simeq B$
if and only if there is a contractive isomorphism
![]() $U(A) \simeq U(B)$
.
$U(A) \simeq U(B)$
.
Proof. Its clear that two isomorphic C*-algebras have isomorphic unitary groups. On the other hand, if
![]() $U(A) \simeq U(B)$
, then since these C*-algebras are
$U(A) \simeq U(B)$
, then since these C*-algebras are
![]() $\mathcal{Z}$
-stable, Corollary 4.9 applies. As
$\mathcal{Z}$
-stable, Corollary 4.9 applies. As
![]() $KT_u(\cdot )$
recovers the Elliott invariant, which is a complete invariant for the C*-algebras as in the statement of the theorem (by [Reference Castillejos, Evington, Tikuisis, White and Winter5, Corollary D], [Reference Elliott, Guihua Gong and Niu16, Reference Gong, Lin and Niu18, Reference Gong, Lin and Niu19] and the references therein),
$KT_u(\cdot )$
recovers the Elliott invariant, which is a complete invariant for the C*-algebras as in the statement of the theorem (by [Reference Castillejos, Evington, Tikuisis, White and Winter5, Corollary D], [Reference Elliott, Guihua Gong and Niu16, Reference Gong, Lin and Niu18, Reference Gong, Lin and Niu19] and the references therein),
![]() $A \simeq B$
.
$A \simeq B$
.
Using the state-of-the art classification of embeddings [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6], there is an enlarged invariant of
![]() $KT_u(\cdot )$
, which is able to classify morphisms between certain C*-algebras. Any
$KT_u(\cdot )$
, which is able to classify morphisms between certain C*-algebras. Any
![]() $KT_u$
-morphisms automatically has a lift to this larger invariant [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6, Theorem 3.9], and so under the assumption that the
$KT_u$
-morphisms automatically has a lift to this larger invariant [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6, Theorem 3.9], and so under the assumption that the
![]() $KT_u$
-morphism is faithful (i.e., the map
$KT_u$
-morphism is faithful (i.e., the map
![]() $T(B) \to T(A)$
induced by the map
$T(B) \to T(A)$
induced by the map
![]() $\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
sends traces on
$\textrm{Aff}\, T(A) \to \textrm{Aff}\, T(B)$
sends traces on
![]() $B$
to faithful traces on
$B$
to faithful traces on
![]() $A$
), there is a *-homomorphism witnessing the
$A$
), there is a *-homomorphism witnessing the
![]() $KT_u$
-morphism. Therefore, as a corollary of their main theorem, we have that for an abundance of C*-algebras, there is an (contractive) embedding of unitary groups if and only if there is an embedding of C*-algebras.
$KT_u$
-morphism. Therefore, as a corollary of their main theorem, we have that for an abundance of C*-algebras, there is an (contractive) embedding of unitary groups if and only if there is an embedding of C*-algebras.
Corollary 4.13.
Let
![]() $A$
be a unital, separable, simple nuclear C*-algebra satisfying the UCT which is either
$A$
be a unital, separable, simple nuclear C*-algebra satisfying the UCT which is either
![]() $\mathcal{Z}$
-stable or of stable rank one and
$\mathcal{Z}$
-stable or of stable rank one and
![]() $B$
be a unital, separable, simple, nuclear
$B$
be a unital, separable, simple, nuclear
![]() $\mathcal{Z}$
-stable C*-algebra. If there is a contractive injective homomorphism
$\mathcal{Z}$
-stable C*-algebra. If there is a contractive injective homomorphism
![]() $\theta \,:\,U(A) \to U(B)$
such that
$\theta \,:\,U(A) \to U(B)$
such that
![]() $\theta (\mathbb{T}) = \mathbb{T}$
, then there is an embedding
$\theta (\mathbb{T}) = \mathbb{T}$
, then there is an embedding
![]() $A \hookrightarrow B$
.
$A \hookrightarrow B$
.
Proof. Assuming such a
![]() $\theta$
exists, it gives rise to a
$\theta$
exists, it gives rise to a
![]() $KT_u$
-morphism
$KT_u$
-morphism
by Corollary 4.10. As
![]() $A,B$
are simple, the map
$A,B$
are simple, the map
![]() $T_\theta \,:\, T(B) \to T(A)$
necessarily maps traces on
$T_\theta \,:\, T(B) \to T(A)$
necessarily maps traces on
![]() $B$
to faithful traces on
$B$
to faithful traces on
![]() $A$
, and thus the
$A$
, and thus the
![]() $KT_u$
-morphism
$KT_u$
-morphism
![]() $KT_u(\theta )$
is “faithful.” Therefore,
$KT_u(\theta )$
is “faithful.” Therefore,
![]() $KT_u(\theta )$
induces an embedding
$KT_u(\theta )$
induces an embedding
![]() $A \hookrightarrow B$
by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6, Theorem B].
$A \hookrightarrow B$
by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6, Theorem B].
5. A slight general linear variant
Here, we briefly describe a slight general linear variant of some of the results above. Unfortunately, the maps we get at the level of
![]() $A,B$
and complex-valued continuous affine functions are not
$A,B$
and complex-valued continuous affine functions are not
![]() $\mathbb{C}$
-linear in general (see Example 5.3). In the presence of a continuous homomorphism
$\mathbb{C}$
-linear in general (see Example 5.3). In the presence of a continuous homomorphism
![]() $\theta \,:\, GL^0(A) \to GL^0(B)$
, we have corresponding maps
$\theta \,:\, GL^0(A) \to GL^0(B)$
, we have corresponding maps

Again, by modding out by algebraic commutator subgroups when
![]() $DGL^0(A) = \ker \Delta _A^1$
and
$DGL^0(A) = \ker \Delta _A^1$
and
![]() $DGL^0(B) = \ker \Delta _B^1$
(both with respect to the general linear variant of the de la Harpe–Skandalis determinant, as originally introduced in [Reference de la Harpe and Skandalis12]), instead of closures of derived groups, there is a purely algebraic variant of the above diagram:
$DGL^0(B) = \ker \Delta _B^1$
(both with respect to the general linear variant of the de la Harpe–Skandalis determinant, as originally introduced in [Reference de la Harpe and Skandalis12]), instead of closures of derived groups, there is a purely algebraic variant of the above diagram:

Thinking of
![]() $K_0(A)$
as the Grothendieck group of the semigroup of equivalence classes of idempotents and
$K_0(A)$
as the Grothendieck group of the semigroup of equivalence classes of idempotents and
![]() $K_0(A) \simeq \pi _1(GL_{\infty }^0(A))$
, we would like to lift the maps on the right of (5.1) and (5.2) to a map
$K_0(A) \simeq \pi _1(GL_{\infty }^0(A))$
, we would like to lift the maps on the right of (5.1) and (5.2) to a map
(the latter holding true when
![]() $A,B$
are C*-algebras whose determinant has appropriate kernel).
$A,B$
are C*-algebras whose determinant has appropriate kernel).
We can always achieve a bounded
![]() $\mathbb{R}$
-linear map.
$\mathbb{R}$
-linear map.
Proposition 5.1.
Let
![]() $A,B$
be unital C*-algebras and
$A,B$
be unital C*-algebras and
![]() $\theta \,:\, GL^0(A) \to GL^0(B)$
be a continuous group homomorphism. Then there is a continuous
$\theta \,:\, GL^0(A) \to GL^0(B)$
be a continuous group homomorphism. Then there is a continuous
![]() $\mathbb{R}$
-linear map
$\mathbb{R}$
-linear map
which lifts the maps on the right of (
5.1
) and (
5.2
) (the latter holding when
![]() $DGL^0(A) = \ker \Delta _A^1$
and
$DGL^0(A) = \ker \Delta _A^1$
and
![]() $DGL^0(B) = \ker \Delta _B^1$
).
$DGL^0(B) = \ker \Delta _B^1$
).
Proof. We define
![]() $G_\theta \,:\, A \to B$
given by
$G_\theta \,:\, A \to B$
given by
We note that the sequence on the right is eventually constant: choose
![]() $N$
large enough such that
$N$
large enough such that
![]() $n \geq N$
implies that
$n \geq N$
implies that
We then have for
![]() $n \geq N$
,
$n \geq N$
,
 \begin{align} \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{n}}\right) &= \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{Na}{Nn}}\right) \nonumber\\[4pt] &= \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right)^N \nonumber\\[4pt] &= \frac{Nn}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right) \nonumber\\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right)^n \\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{na}{Nn}}\right)\nonumber \\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{N}}\right).\nonumber \end{align}
\begin{align} \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{n}}\right) &= \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{Na}{Nn}}\right) \nonumber\\[4pt] &= \frac{n}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right)^N \nonumber\\[4pt] &= \frac{Nn}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right) \nonumber\\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{Nn}}\right)^n \\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{na}{Nn}}\right)\nonumber \\[4pt] &= \frac{N}{2\pi i}\log \theta \left(e^{2\pi i \frac{a}{N}}\right).\nonumber \end{align}
To see that the map is additive, one can use the Lie product formula
(see for example [Reference Hall23, Theorem 2.11]), along with the fact that
![]() $\theta$
is a continuous homomorphism. From here, it is clear that
$\theta$
is a continuous homomorphism. From here, it is clear that
![]() $G_\theta$
is continuous and
$G_\theta$
is continuous and
![]() $\mathbb{Q}$
-linear, hence
$\mathbb{Q}$
-linear, hence
![]() $\mathbb{R}$
-linear. Moreover, one can use the formula
$\mathbb{R}$
-linear. Moreover, one can use the formula
(a variation of the argument given in the proof of [Reference Hall23, Theorem 2.11] will give the desired formula), together with
![]() $\theta$
being a continuous group homomorphism, to show that it respects commutation. Note that the same proof indeed shows that
$\theta$
being a continuous group homomorphism, to show that it respects commutation. Note that the same proof indeed shows that
![]() $S_\theta$
respects commutation, although we never explicitly used this. From here,
$S_\theta$
respects commutation, although we never explicitly used this. From here,
![]() $G_\theta ([A,A]) \subseteq [B,B]$
, and consequently,
$G_\theta ([A,A]) \subseteq [B,B]$
, and consequently,
![]() $G_\theta (\overline{[A,A]}) \subseteq \overline{[B,B]}$
by continuity. Thus, there is an induced
$G_\theta (\overline{[A,A]}) \subseteq \overline{[B,B]}$
by continuity. Thus, there is an induced
![]() $\mathbb{R}$
-linear map
$\mathbb{R}$
-linear map
The fact that
![]() $\tilde{G}_\theta$
is a lift of the maps on the right of (5.1) and (5.2) follows from the same arguments as in Propositions 3.7 and 3.8.
$\tilde{G}_\theta$
is a lift of the maps on the right of (5.1) and (5.2) follows from the same arguments as in Propositions 3.7 and 3.8.
Remark 5.2.
We note that
![]() $G_\theta$
could have also been defined in the same manner as
$G_\theta$
could have also been defined in the same manner as
![]() $S_\theta$
. In particular, there is a correspondence
$S_\theta$
. In particular, there is a correspondence
One can use this to show that
![]() $\theta (\ker \Delta _A^1) \subseteq \ker \Delta _B^1$
as in Proposition 3.5 by using
$\theta (\ker \Delta _A^1) \subseteq \ker \Delta _B^1$
as in Proposition 3.5 by using
![]() $G_\theta$
in place of
$G_\theta$
in place of
![]() $S_\theta$
, along with the fact that
$S_\theta$
, along with the fact that
![]() $G_\theta (\overline{[A,A]}) \subseteq \overline{[B,B]}$
. So there will always be a general linear variant of the commuting diagram (
3.4
).
$G_\theta (\overline{[A,A]}) \subseteq \overline{[B,B]}$
. So there will always be a general linear variant of the commuting diagram (
3.4
).
Let us use (5.11) to show that the maps
![]() $G_\theta$
and
$G_\theta$
and
![]() $\tilde{G}_\theta$
in Proposition 5.1 are not always
$\tilde{G}_\theta$
in Proposition 5.1 are not always
![]() $\mathbb{C}$
-linear.
$\mathbb{C}$
-linear.
Example 5.3.
Consider
![]() $A = B = \mathbb{C}$
and
$A = B = \mathbb{C}$
and
![]() $\theta \,:\, \mathbb{C}^\times \to \mathbb{C}^\times$
given by
$\theta \,:\, \mathbb{C}^\times \to \mathbb{C}^\times$
given by
![]() $\theta (z) = |z|^{(\alpha + \beta i)}z^n$
where
$\theta (z) = |z|^{(\alpha + \beta i)}z^n$
where
![]() $\alpha,\beta \in \mathbb{R}$
and
$\alpha,\beta \in \mathbb{R}$
and
![]() $n \in \mathbb{Z}$
. It is easy to see that
$n \in \mathbb{Z}$
. It is easy to see that
![]() $\theta$
is a continuous group homomorphism. However, the map
$\theta$
is a continuous group homomorphism. However, the map
![]() $G_\theta$
is not
$G_\theta$
is not
![]() $\mathbb{C}$
-linear. Indeed, we have that
$\mathbb{C}$
-linear. Indeed, we have that
 \begin{equation} \begin{split} \theta \left(e^{2\pi i t(a+bi)}\right) &= \left|e^{2\pi i t(a + bi)}\right|^{\alpha + \beta i}e^{2\pi i t n(a + bi)} \\ &= \left(e^{-2\pi t b}\right)^{\alpha + \beta i}e^{2\pi i t n(a + bi)} \\ &= e^{-2\pi t b\alpha }e^{-2\pi i t\beta i b}e^{2\pi i t n(a + bi)} \\ &= e^{2\pi i t((na - \alpha b) + i(n - \beta )b}. \end{split} \end{equation}
\begin{equation} \begin{split} \theta \left(e^{2\pi i t(a+bi)}\right) &= \left|e^{2\pi i t(a + bi)}\right|^{\alpha + \beta i}e^{2\pi i t n(a + bi)} \\ &= \left(e^{-2\pi t b}\right)^{\alpha + \beta i}e^{2\pi i t n(a + bi)} \\ &= e^{-2\pi t b\alpha }e^{-2\pi i t\beta i b}e^{2\pi i t n(a + bi)} \\ &= e^{2\pi i t((na - \alpha b) + i(n - \beta )b}. \end{split} \end{equation}
In particular, thinking of
![]() $\mathbb{C}$
as
$\mathbb{C}$
as
![]() $\mathbb{R}^2$
with 1 and
$\mathbb{R}^2$
with 1 and
![]() $i$
corresponding to the basis vectors
$i$
corresponding to the basis vectors
![]() $(1,0)$
and
$(1,0)$
and
![]() $(0,1)$
, respectively, we have that
$(0,1)$
, respectively, we have that
![]() $G_\theta \,:\, \mathbb{R}^2 \to \mathbb{R}^2$
is the map
$G_\theta \,:\, \mathbb{R}^2 \to \mathbb{R}^2$
is the map
 \begin{equation} G_\theta \begin{pmatrix} a \\[3pt] b \end{pmatrix} = \begin{pmatrix} n & \quad -\alpha \\[3pt] 0 & \quad n - \beta \end{pmatrix}\begin{pmatrix} a \\[3pt] b \end{pmatrix}. \end{equation}
\begin{equation} G_\theta \begin{pmatrix} a \\[3pt] b \end{pmatrix} = \begin{pmatrix} n & \quad -\alpha \\[3pt] 0 & \quad n - \beta \end{pmatrix}\begin{pmatrix} a \\[3pt] b \end{pmatrix}. \end{equation}
In this example, the map
![]() $G_\theta$
is
$G_\theta$
is
![]() $\mathbb{C}$
-linear if and only if
$\mathbb{C}$
-linear if and only if
![]() $\alpha = \beta = 0$
. We do note, however, that
$\alpha = \beta = 0$
. We do note, however, that
![]() $\theta$
sends unitaries to unitaries and
$\theta$
sends unitaries to unitaries and
![]() $\theta |_{\mathbb{T}}(z) = z^n$
.
$\theta |_{\mathbb{T}}(z) = z^n$
.
In general, it is clear that if
![]() $\theta \,:\, GL(A) \to GL(B)$
sends unitaries to unitaries, then we can use techniques in Section 4 to get maps between spaces of continuous affine functions on the trace simplices. If one had that
$\theta \,:\, GL(A) \to GL(B)$
sends unitaries to unitaries, then we can use techniques in Section 4 to get maps between spaces of continuous affine functions on the trace simplices. If one had that
![]() $\theta$
was the restriction of a *-homomorphism or a conjugate-linear *-homomorphism, then this would be true.
$\theta$
was the restriction of a *-homomorphism or a conjugate-linear *-homomorphism, then this would be true.
6. Final remarks and open questions
An alternate way to construct the map
![]() $\Lambda _\theta$
, using duality of traces, is as follows. Denote by
$\Lambda _\theta$
, using duality of traces, is as follows. Denote by
![]() $\mathfrak{T}_s(A)$
the set of all tracial functionals on
$\mathfrak{T}_s(A)$
the set of all tracial functionals on
![]() $A$
. Suppose that
$A$
. Suppose that
![]() $A,B$
are unital C*-algebras with
$A,B$
are unital C*-algebras with
![]() $T(A),T(B) \neq \emptyset$
, and
$T(A),T(B) \neq \emptyset$
, and
![]() $\theta \,:\, U^0(A) \to U^0(B)$
is a continuous homomorphism. Define, for
$\theta \,:\, U^0(A) \to U^0(B)$
is a continuous homomorphism. Define, for
![]() $a \in A_{sa}$
and
$a \in A_{sa}$
and
![]() $\tau \in \mathfrak{T}_s(B)$
,
$\tau \in \mathfrak{T}_s(B)$
,
Proposition 6.1.
For
![]() $\tau \in \mathfrak{T}_s(B)$
, the map
$\tau \in \mathfrak{T}_s(B)$
, the map
![]() $F(\tau )\,:\, A_{sa} \to \mathbb{R}$
is a well-defined, bounded, self-adjoint, tracial functional. Moreover,
$F(\tau )\,:\, A_{sa} \to \mathbb{R}$
is a well-defined, bounded, self-adjoint, tracial functional. Moreover,
![]() $F\,:\, \mathfrak{T}_s(B) \to \mathfrak{T}_s(A)$
given by
$F\,:\, \mathfrak{T}_s(B) \to \mathfrak{T}_s(A)$
given by
![]() $\tau \mapsto F(\tau )$
is a bounded
$\tau \mapsto F(\tau )$
is a bounded
![]() $\mathbb{R}$
-linear map.
$\mathbb{R}$
-linear map.
Proof. Using the same arguments as in Proposition 5.1, it is clear the formula (6.1) is well defined and gives rise to a bounded
![]() $\mathbb{R}$
-linear map
$\mathbb{R}$
-linear map
![]() $F\,:\, \mathfrak{T}_s(B) \to \mathfrak{T}_s(A)$
.
$F\,:\, \mathfrak{T}_s(B) \to \mathfrak{T}_s(A)$
.
One can identify
![]() $\left (A_{sa}/A_0\right )^* \simeq \mathfrak{T}_s(A)$
(see, e.g., [Reference Cuntz and Pedersen8]), and so we can use duality to get a map
$\left (A_{sa}/A_0\right )^* \simeq \mathfrak{T}_s(A)$
(see, e.g., [Reference Cuntz and Pedersen8]), and so we can use duality to get a map
![]() $\tilde{\Lambda }_\theta \,:\!=\, F^*\,:\, \mathfrak{T}_s(A)^* \to \mathfrak{T}_s(B)^*$
and restrict it to the dense set
$\tilde{\Lambda }_\theta \,:\!=\, F^*\,:\, \mathfrak{T}_s(A)^* \to \mathfrak{T}_s(B)^*$
and restrict it to the dense set
![]() $A_{sa}/A_0$
. One can check that the image lies in
$A_{sa}/A_0$
. One can check that the image lies in
![]() $B_{sa}/B_0$
and that the restriction is just the map
$B_{sa}/B_0$
and that the restriction is just the map
![]() $\Lambda _\theta$
that we got before.
$\Lambda _\theta$
that we got before.
We finish by listing some open problems.
-
1. There are classes where topological isomorphisms between
 $U(A)$
and
$U(A)$
and
 $U(B)$
(or even
$U(B)$
(or even
 $U^0(A)$
and
$U^0(A)$
and
 $U^0(B)$
) come from *-isomorphisms or anti-*-isomorphisms. For example, if
$U^0(B)$
) come from *-isomorphisms or anti-*-isomorphisms. For example, if
 $A,B$
are prime traceless C*-algebras containing full square zero elements, this is true by results in [Reference Chand and Robert9].
$A,B$
are prime traceless C*-algebras containing full square zero elements, this is true by results in [Reference Chand and Robert9].If
 $A$
is a unital, separable, nuclear C*-algebra satisfying the UCT and
$A$
is a unital, separable, nuclear C*-algebra satisfying the UCT and
 $B$
is a unital simple separable nuclear
$B$
is a unital simple separable nuclear
 $\mathcal{Z}$
-stable C*-algebra, then unital embeddings
$\mathcal{Z}$
-stable C*-algebra, then unital embeddings
 $A \hookrightarrow B$
are classified by an invariant
$A \hookrightarrow B$
are classified by an invariant
 $\underline{K}T_u(\cdot )$
, which is an enlargement of
$\underline{K}T_u(\cdot )$
, which is an enlargement of
 $KT_u$
[Reference Carrión, Gabe, Schafhauser, Tikuisis and White6]. Thus, any isometric unitary group homomorphism
$KT_u$
[Reference Carrión, Gabe, Schafhauser, Tikuisis and White6]. Thus, any isometric unitary group homomorphism
 $U(A) \to U(B)$
will give a
$U(A) \to U(B)$
will give a
 $KT_u$
-morphism
$KT_u$
-morphism
 $KT_u(\theta )$
and therefore there will be an embedding
$KT_u(\theta )$
and therefore there will be an embedding
 $\phi \,:\,A \hookrightarrow B$
such that
$\phi \,:\,A \hookrightarrow B$
such that
 $KT_u(\phi ) = KT_u(\theta )$
. However, it is not clear that
$KT_u(\phi ) = KT_u(\theta )$
. However, it is not clear that
 $\phi$
satisfies
$\phi$
satisfies
 $\phi |_{U(A)} = \theta$
. More generally though – in the tracial setting – are there continuous group homomorphisms which do not have lifts to *-homomorphisms or anti-*-homomorphisms?
$\phi |_{U(A)} = \theta$
. More generally though – in the tracial setting – are there continuous group homomorphisms which do not have lifts to *-homomorphisms or anti-*-homomorphisms?Note that in [Reference Ara and Mathieu1, Chapter 6], Lie isomorphisms between certain C*-algebras are shown to be the sum of a Jordan *-isomorphism and a center-valued trace. Is there a result for general (injective) Lie homomorphisms between certain classes of C*-algebras?
-
2. This enlargement of
 $KT_u$
discussed in [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6] contains
$KT_u$
discussed in [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6] contains
 $K$
-theory with coefficients (along with appropriate pairing maps—the Bosckstein maps discussed in [Reference Schochet37]). So we ask: do continuous group homomorphisms induce maps between
$K$
-theory with coefficients (along with appropriate pairing maps—the Bosckstein maps discussed in [Reference Schochet37]). So we ask: do continuous group homomorphisms induce maps between
 $K$
-theory with coefficients?
$K$
-theory with coefficients? -
3. For a general continuous homomorphism
 $\theta \,:\, U^0(A) \to U^0(B)$
, does the norm
$\theta \,:\, U^0(A) \to U^0(B)$
, does the norm
 $\|S_\theta \|$
determine a Lipschitz constant for
$\|S_\theta \|$
determine a Lipschitz constant for
 $\theta$
? We clearly have that(6.2)by Lemma 4.4. Is this equality?
$\theta$
? We clearly have that(6.2)by Lemma 4.4. Is this equality? \begin{equation} \|S_\theta \| \leq \inf \{ K \mid \theta \text{ is }K\text{-Lipschitz}\} \end{equation}
\begin{equation} \|S_\theta \| \leq \inf \{ K \mid \theta \text{ is }K\text{-Lipschitz}\} \end{equation}
-
4. For
 $A$
simple (or prime), is it true that any continuous injective homomorphism
$A$
simple (or prime), is it true that any continuous injective homomorphism
 $\theta \,:\, U^0(A) \to U^0(B)$
is isometric? Contractive? What if
$\theta \,:\, U^0(A) \to U^0(B)$
is isometric? Contractive? What if
 $B$
is simple (or prime)?
$B$
is simple (or prime)? -
5. In the initial draft of this paper, we claimed that any continuous group homomorphism in Proposition 5.1 gave rise to a
 $\mathbb{C}$
-linear
$\mathbb{C}$
-linear
 $\tilde{G}_\theta$
. This is clearly false by Example 5.3. Is there a way to guarantee that the map
$\tilde{G}_\theta$
. This is clearly false by Example 5.3. Is there a way to guarantee that the map
 $\tilde{G}_\theta$
is
$\tilde{G}_\theta$
is
 $\mathbb{C}$
-linear? Or can one alter it accordingly for this to happen? Or alter it to get a map between unitary groups, which would then allow one to use the results in Section 4? Maybe if one starts with an injective, contractive group homomorphism
$\mathbb{C}$
-linear? Or can one alter it accordingly for this to happen? Or alter it to get a map between unitary groups, which would then allow one to use the results in Section 4? Maybe if one starts with an injective, contractive group homomorphism
 $GL^0(A) \to GL^0(B)$
which sends
$GL^0(A) \to GL^0(B)$
which sends
 $\mathbb{C}^\times$
to
$\mathbb{C}^\times$
to
 $\mathbb{C}^\times$
, one can say something.
$\mathbb{C}^\times$
, one can say something.
Acknowledgments
Many thanks to my PhD supervisors Thierry Giordano and Aaron Tikuisis for many helpful discussions. Thanks to the authors of [Reference Carrión, Gabe, Schafhauser, Tikuisis and White6] for sharing a draft of their paper. Finally, thanks to the referee for asking for clarification on the general linear variant, which led me to consider a counterexample to
![]() $\mathbb{C}$
-linearity.
$\mathbb{C}$
-linearity.