1. Introduction
The principal processes affecting the mass balance and dynamics of the ice sheets are illustrated in Figure 1, including interactions with the atmosphere and ocean. The principal ice-mass input is from atmospheric precipitation in the form of snowfall, with subsequent losses from sublimation, snow redistribution by surface winds, and drift removal at the margins. In Greenland, surface melting in the ablation zone causes water runoff from the grounded ice and acceleration of the ice flow as meltwater propagates to the ice-sheet base to enhance basal sliding. In contrast, surface melting on the grounded ice of Antarctica is very small, and subject to refreezing in the firn, with negligible mass loss. Interaction with the ocean occurs at the undersides of the floating ice shelves and glacier tongues, with ocean melting of the basal ice or accretion of ice from basal freezing. Consequent changes in the thickness of floating ice affect the rate of ice flow from the grounded ice.
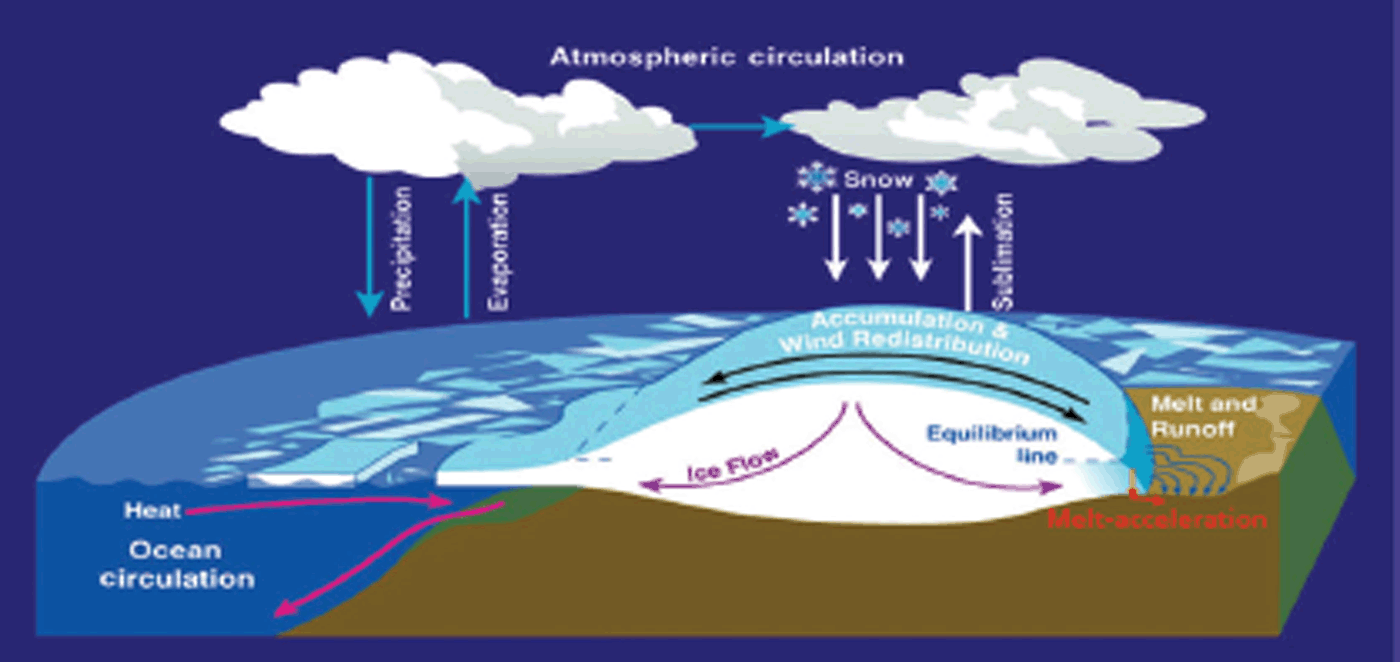
Fig. 1. The principal processes affecting the mass balance and dynamics of the ice sheets are ice mass input from snowfall with losses from sublimation and drifting. Surface melting on the grounded ice of Antarctica is very small, and subject to refreezing in the firn. Interaction with the ocean occurs at the undersides of the floating ice shelves and glacier tongues, and consequent changes in thickness affect the rate of ice flow from the grounded ice.
The annual mass input to the Antarctic ice sheet (AIS) from snow accumulation is ∼2000 Gt a−1, based on field data (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000) and meteorological data (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). By 2011, estimates of the mass balance (input–output) of Antarctica had improved from roughly 0 ± 400 Gt a−1 in the mid-1990s to a range of approximately +50 to −250 Gt a−1 for the period 1992–2009 (Reference Zwally and GiovinettoZwally and Giovinetto, 2011). The principal techniques have been based on satellite technology: (1) elevation and volume change from radar altimetry (RA) and laser altimetry (LA), (2) mass change from gravimetry (GR), and (3) the input–output method (IOM) using ice-velocity sensing for mass output estimates. Subsequent evaluation (Reference ShepherdShepherd and others, 2012) eliminated some of the larger estimates of Antarctic mass loss and gave a mean estimate of −72 ± 43 Gt a−1 from the four techniques (RA, LA, GR and IOM) for the intercomparison period October 2003 to December 2008. Despite the progress, significant uncertainties remained about rates of mass change for various reasons (Reference HannaHanna and others, 2013), especially for East Antarctica (EA). Despite residual uncertainties, the general pattern of gains and losses has been a net mass loss from coastal regions of West Antarctica (WA) and the Antarctic Peninsula (AP), acceleration of those losses during the last 20 years, and a net mass gain in EA (Reference Zwally and GiovinettoZwally and Giovinetto, 2011; Reference ShepherdShepherd and others, 2012; Reference HannaHanna and others, 2013).
Variations in the surface mass balance (SMB) and vertical ice velocity of the grounded ice sheet both cause changes in net mass balance (dM/dt) and surface elevations (dH/dt). Over Antarctica, the rate of total mass change per unit area is principally the sum of surface balance, dM a/dt, and dynamic-driven mass change, dM d/dt:
The dynamic dM d/dt is defined by differences between the vertical ice flux from the surface and the long-term (>decades) average accumulation rate 〈A〉. dM a/dt is driven by short-term (<decades) variations in the accumulation rate. In our analysis, any net changes in ice thickness caused by melting or freezing at the base of grounded ice are neglected and are therefore essentially included in the dynamic term. The dM d/dt may be caused by either dynamic variations in ice velocity on various timescales or by persistent long-term changes in 〈A〉 with a consequent long-term dynamic response.
The essential characteristic of both dynamic thickening (dH d/dt > 0 and dM d/dt > 0) (Reference Li and ZwallyZwally and others, 2011) and dynamic thinning (dH d/dt < 0 and dM d/dt < 0 ) (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009; Reference Filament and RémyFilament and Rémy, 2012) is a difference between the vertical ice flux from the surface and 〈A〉. Information on the timing of changes in dynamic thinning or thickening is only provided if observed dH d/dt differ between measurement periods. Interpretation of changes in dH d/dt on longer timescales (>decadal) requires additional information such as variations in accumulation rates from ice cores.
In this paper, we determine the values of the mass terms in Eqn (1) in 50 km × 50 km gridcells over the AIS using satellite-altimeter measurements of dH/dt along with meteorological data on accumulation variations. We use radar-altimeter measurements of dH/dt by European Remote-sensing Satellites 1 and 2 (ERS-1/-2) for the period 1992–2001 and satellite laser-altimeter measurements by the Ice, Cloud and land Elevation Satellite (ICESat) for 2003–08. Our procedures (Reference Li and ZwallyLi and Zwally, 2011; Reference ZwallyZwally and others, 2011) for deriving dM/dt from measured dH/dt apply height corrections for factors that do not change the ice mass, specifically vertical motion of the underlying bedrock (dB/dt) and changes in the vertical velocity (V fc) of the surface due to variations in the rate of firn compaction (FC). The dM a/dt during elevation measurement periods are calculated directly from the accumulation variations, δA(t), provided by meteorological reanalysis data relative to their 27 year average (1982–2008).
We analyze our derived dM/dt, and its dM a/dt and dM d/dt components, in 27 drainage systems (DS) (http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php), and the major regions of WA, EA and the AP as shown in Figure 2. Grounded ice on adjacent islands and ice rises within ice shelves is included in the respective DS. WA is divided into WA1 (consisting of three dynamically active coastal DS that include Pine Island, Thwaites and Smith glaciers and the coastal DS of Marie Byrd Land) and WA2 (consisting of three inland DS flowing into the Ross and Filchner Ice Shelves and a small coastal DS at the base of the AP). EA is also divided into the westernmost EA1 consisting of DS2–11 and the easternmost EA2 consisting of DS12–17, in order to illustrate differences in their meteorological variations. We discuss the glaciological and climatological significance of the derived rates of mass change, including significant temporal changes between the 1992–2001 and 2003–08 measurement periods and the absence of significant temporal changes in certain DS and regions.
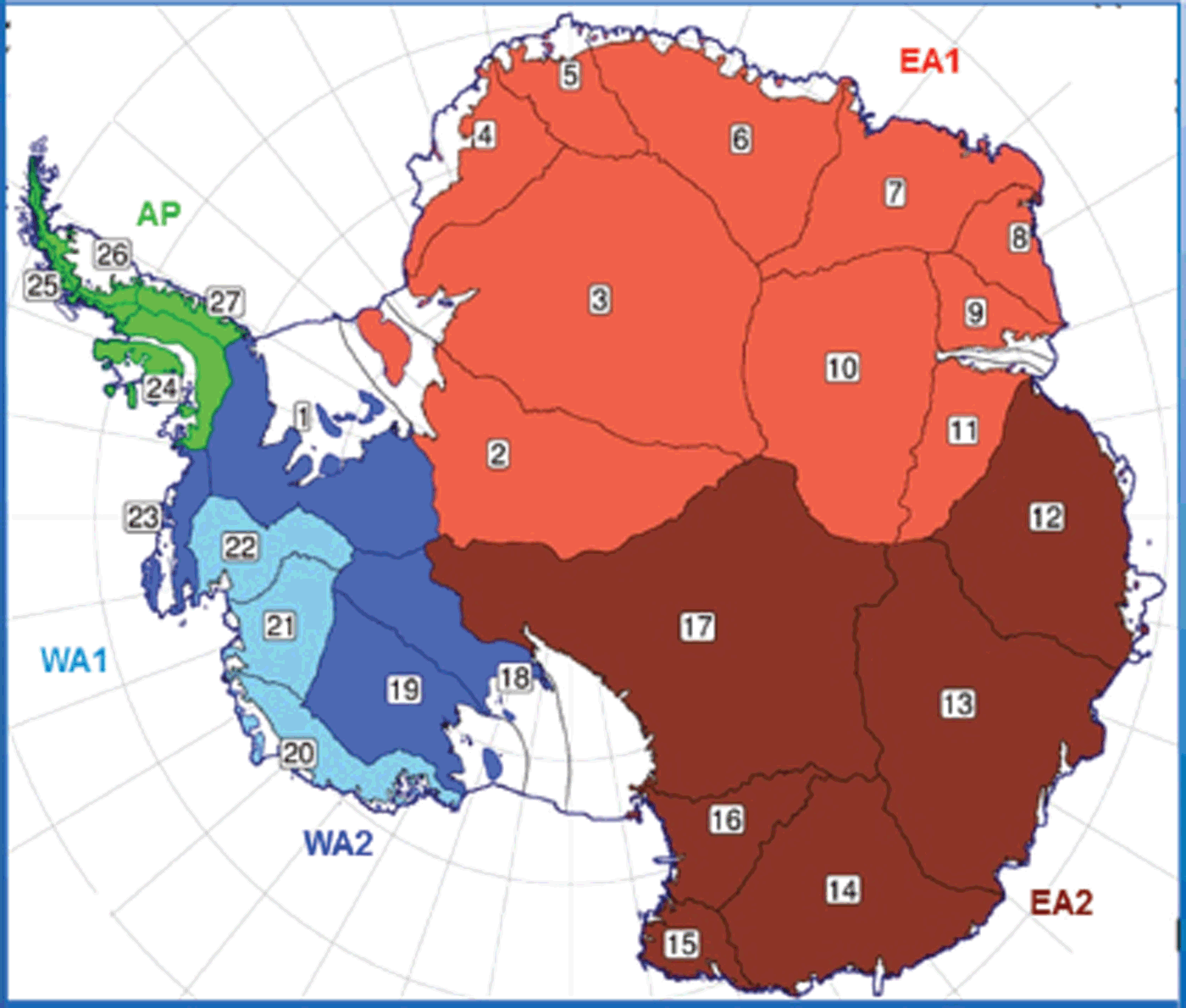
Fig. 2. Antarctic drainage systems and regions. The Antarctic Peninsula (AP) with DS24–27. West Antarctica (WA) is divided into WA1 (Pine Island Glacier DS22, Thwaites and Smith Glaciers DS21 and the coastal DS20) and WA2 (coastal DS23 and inland DS1, DS18 and DS19). East Antarctica (EA) is divided into EA1 (DS2–11) and EA2 (DS12–17).
2. Altimeter Data, Elevation Change Solutions and dH/dT Maps
For 1992–2001, we use previous gridded dH/dt (Reference ZwallyZwally and others, 2005) that were calculated from time series of elevation differences at orbital crossovers of ERS-1 and ERS-2 radar altimeter data (http://icesat4.gsfc.nasa.gov/) from mid-April 1992 to mid-April 2001. The instrument, range retracking, ERS-1/ERS-2 bias and other corrections, as well as the use of DUT DGM-E04 orbits which have a radial orbit precision of 5–6 cm (Reference Scharroo and VisserScharroo and Visser, 1998), are described in Zwally and others (Reference Zwally2005; http://icesat4.gsfc. nasa.gov/). Principal changes in our analysis for the ERS period are the separation of accumulation-driven and dynamic-driven changes and the dB/dt correction that uses a more recent model on bedrock motion (Section 3).
For 2003–08, we use ICESat data release 634 (http://nsidc.org/data/icesat/index.html) for 15 laser campaigns (each with data for 33 to ∼36 days) from October 2003 to October/mid-December 2008. The surface elevations in release 634 data products were changed from release 633 by application of the Gaussian–centroid (G-C) range correction (see Appendix), which also significantly increased the need for laser campaign bias corrections to obtain accurate elevation changes (Reference ZwallyZwally, 2013). We apply ICESat laser campaign bias corrections derived from laser measurements of the sea surface height (SSH) over open water and thin ice in leads and polynyas within the Antarctic and Arctic sea-ice packs, with adjustments for SSH variations measured by Envisat radar altimetry concurrently with ICESat measurements (see Appendix). We calculate dh/dt at equally spaced (172 m) reference points on a set of ICESat reference tracks for points where sufficient data (i.e. N ≥4 satellite passes) are available, solving simultaneously by linear least-squares minimization for dh/dt, cross-track surface slope (α) and elevation (h trk(t 0)) on the reference track at time t 0 (Reference ZwallyZwally and others, 2011). Data on parallel repeat passes are first interpolated to the locations on the tracks perpendicular to each reference point. Solutions at each reference point also include data at three points before and after the reference point. We account for the along-track slope by first calculating it separately from a fit of the data from all tracks to a surface curved in the along-track direction. To extend the analysis beyond the ICESat campaigns through 2007 that have cloud flags in the data records previously used for editing, we developed multi-stage data-editing criteria that gave essentially the same dM/dt results (i.e. −173 Gt a−1 versus −171 Gt a−1 for 2003–07 for Greenland in Reference ZwallyZwally and others, 2011). In the first stage, we use all ICESat data for which valid surface elevations are indicated and iteratively exclude 3σ outliers from the curved surface in the least-squares solution. The maps of dh/dt and dh/dt over grounded ice are presented in Figure 3. The second stage excludes dh/dt outliers in the averaging of dH/dt into gridcell maps of dH/dt.

Fig. 3. Along-track solutions at 172 m spacing in Antarctica from ICESat data. (a) dh/dt, and (b) σ dh/dt showing σ dh/dt is mostly <0.05 m a−1, with larger values at margins where dh/dt tend to be larger.
The calculated along-track profiles of dh/dt and Δh(ti ) over Smith Glacier in DS21 in Figure 4 illustrate the quality of the solutions in a region of large thinning near the coast in WA. The maximum rate of surface lowering on track 1300 over Smith Glacier is 9 m a−1, resulting in a 48 m lowering in 5.5 years. Figure 5 illustrates the variations of dh/dt in a region of small changes over Vostok Subglacial Lake in EA, where dh/dt varies from approximately +0.0 ± 1 cm a−1 to +3.0 ± 1 cm a−1 with km-scale oscillations and significant spatial variability of average values over the lake. Other features of the dh/dt variability are low dh/dt in the trough on the southwestern end of track 0330, in contrast to the average value there on track 1312, and the above average on track 0077. Near the small ridge on the northeastern side, dh/dt is approximately +2 cm a−1 on track 0330, +1.5 cm a−1 on track 1312, and +0.5 cm a−1 on track 0077.

Fig. 4. Along-track profiles in West Antarctica from ICESat data. (a) Profiles of derived h, dh/dt and σ dh/dt from along-track solutions at 172 m spacing along track 1300 across Smith Glacier in DS21. Maximum dh/dt is −8 m a−1 near the center of the glacier. (b) Surface elevation (Δh(t i)) profiles (ten-point smoothing) relative to the first profile from October 2003 to April 2009. Maximum surface lowering is 48 m in 5.5 years. (c) Along-track dh/dt for the 33 day repeat-cycle tracks plotted on ICESat elevation map.

Fig. 5. Along-track profiles over Vostok Subglacial Lake from ICESat data. (a) Profiles of derived dh/dt, σ dh/dt and h from along-track solutions at 172 m spacing along six tracks. The dh/dt varies from <0 cm a−1 near the northern end of track 0071 to >3.0 cm a−1 on the southern end of track 0077. The σ dh/dt are mostly 1.0 cm a−1. The vertical blue lines indicate crossings of the lake boundary (Reference Tikku, Bell, Studinger and ClarkeTikku and others, 2004). (b) dh/dt for the 33 day repeat-cycle tracks plotted on ICESat elevation map showing outline of the lake.
The spatial variability of dh/dt may be caused by spatial variability of several cm in local values of A(t) from variations in snowdrift, precipitation and sublimation, which also affect the temporal variability of A and elevations at specific locations. Therefore, comparisons between dh/dt from altimetry and surface-based GPS estimates (see Appendix) are highly dependent on the specific locations. A characteristic feature illustrated in Figure 5 is the continuity of dh/dt values on the grounded ice surrounding the lake and the values on the floating ice on the lake. Another interesting feature is the 20 km oscillation in dh/dt between approximately +5 and −2 cm a−1 on the southern end of track 0190, indicating downslope migration of the snow dunes shown on the elevation profiles.
Average values (dH/dt) of the dh/dt in each 50 km gridcell are calculated as previously (Reference ZwallyZwally and others, 2011), and the resulting dH/dt maps for 1992–2001 and 2003–08 are presented in Figure 6. We use kriging (optimal interpolation) to fill the dH/dt gridcells without data south of the 86°S coverage of ICESat, and for some cells at the ice-sheet margins for both ERS and ICESat. For 1992–2001, we use the ICESat dH/dt to fill in the area south of the 81.5°S coverage of ERS. The average dH/dt of 1.96 cm a−1 south of 81.5°S is therefore the same for both ERS and ICESat, but their respective dM/dt values, of 56.0 and 45.9 Gt a−1, differ because dM a/dt, dH a/dt and dC A/dt (Section 3) differ between periods. The results of using the ICESat dH/dt south of 81.5°S in the ERS dH/dt grid compare with the alternative method of kriging, which gave an average dH/dt of 2.35 cm a−1 and dM/dt of 64.1 Gt a−1. However, the distribution among the DS south of 81.5°S and the division between WA and EA are better using the ICESat dH/dt.

Fig. 6. Maps of dH/dt (a) for 1992–2001 from ERS-1 and -2 data (dH/dt from ICESat used south of 81.5°E) and (b) for 2003–08 from ICESat data.
In area-weighted summations for DS and regions, cells partially on grounded ice are weighted accordingly. Cells on DS boundaries are partially assigned in proportion to their coverage in each DS. For ICESat data, the partial-cell coverage of the along-track data at the ice margin is determined by an ice-edge boundary with 1 km resolution. For ERS, dH/dt values in the partial cells (as derived from crossover analysis) are weighted by the area fraction on grounded ice, also determined by the 1 km boundary. For ERS, 152.4 out of 4810.9 cells (counting partial cells as fractions) at the ice-sheet margins are kriged and their average dH/dt is −4.9 cm a−1 compared to +0.50 cm a−1 for all cells. For ICESat, 1.6 out of 4810.9 cells at the ice-sheet margins are kriged and their average dH/dt is −20.3 cm a−1 compared to +0.76 cm a−1 for all cells. Previously, cells for ERS were taken as either totally on-ice or off-ice (Reference ZwallyZwally and others, 2005).
We examine the relative calibration of the ERS radar and ICESat laser altimetry over Vostok Subglacial Lake in central EA, which is a dynamically stable region with low accumulation and small vertical velocities. In this region, short-term dynamic changes that might affect the derived H(t) should be very small. Vostok Subglacial Lake also has technical advantages, because of its flatness and consequent minimization of effects of surface slopes on both the radar and laser altimeter measurements. We use ERS crossover analysis and ICESat along-track solutions within a box (78.6–76.19°S, 101.3–107.0°E) of approximately 63 km × 260 km over Vostok Subglacial Lake.
The resulting H(t) time series from ERS, both before and after the backscatter correction for the variable penetration depth of the radar signal in the firn, and the H(t) time series from ICESat, along with their linear trends are shown in Figure 7. As shown in Table 1, the respective trends for ERS and ICESat are very similar, at 2.03 and 2.02 cm a−1. After correction for dB/dt and dC
T/dt (defined in Section 3), the respective dI/dt are 2.01 and 2.08 cm a−1. After further subtracting the accumulation-driven change
![]() , dH
d/dt are 2.18 and 2.05 cm a−1. The small differences (≤0.13 cm a−1) in these height parameters are a good indication of the close relative calibration of ERS and ICESat, for which we estimate respective systematic calibration errors of 0.20 and 0.15 cm a−1. In addition, over the whole of EA (Table 2), the average dH/dt from ERS and ICESat are 1.11 and 1.30 cm a−1, the dI/dt are 1.19 and 1.44 cm a−1 and the dH
d/dt are 1.58 and 1.59 cm a−1, indicating minimal short-term dynamic change as discussed in Section 5.
, dH
d/dt are 2.18 and 2.05 cm a−1. The small differences (≤0.13 cm a−1) in these height parameters are a good indication of the close relative calibration of ERS and ICESat, for which we estimate respective systematic calibration errors of 0.20 and 0.15 cm a−1. In addition, over the whole of EA (Table 2), the average dH/dt from ERS and ICESat are 1.11 and 1.30 cm a−1, the dI/dt are 1.19 and 1.44 cm a−1 and the dH
d/dt are 1.58 and 1.59 cm a−1, indicating minimal short-term dynamic change as discussed in Section 5.

Fig. 7. H(t) time series on Vostok Subglacial Lake. From ERS 1992–2003 with trend of +2.03 cm a−1 after backscatter correction (red) and +2.18 cm a−1 before backscatter correction (black). From ICESat 2003–08 with trend of +2.02 cm a−1 (blue). The backscatter correction significantly reduces the amplitude of the seasonal variability in the ERS signal.
Table 1. Components of elevation change (cm a−1) over Vostok Subglacial Lake
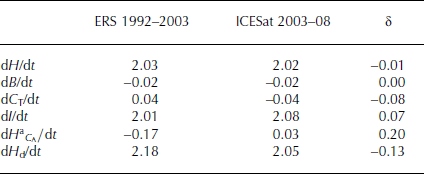
Table 2. Components of surface elevation change (cm a−1), dH/dt, dC
T/dt, dI/dt,
![]() , dH
d/dt, dB/dt by region
, dH
d/dt, dB/dt by region

3. Firn Compaction Modeling, Bedrock Motion, and Calculation of Mass Changes
Calculation of dM/dt mass changes from measured dH/dt requires correction for the dH/dt changes that do not involve changes in ice mass, specifically changes in the vertical velocity (V fc) of the surface due to variations in the rate of FC and motion of the underlying bedrock, dB/dt. Defined as perturbations from steady state, the vertical components of dH/dt are
where dH a/dt is the direct height change driven by accumulation variations (δA(t) = A(t) − 〈A〉), dC A/dt and dC T/dt are changes in V fc(t) driven by δA(t) and temperature variations (T(t)), dH d/dt = −(V ice(t) −〈V ice〉) is the dynamic height change determined by physical changes in velocity relative to the long-term (>decades) average velocity (〈V ice〉=〈A〉/ρ i) at the firn/ice transition, where ρ i is the relative density of ice, and dB/dt is taken to be time-independent over decades.
The dynamic-driven height change is then
where dH/dt is the measured height, and dC T/dt and dC A/dt are calculated with the FC model driven by δA(t) from meteorological reanalysis data and by T(t) from satellite measurements, as described below. The dH a/dt is also calculated from δA(t) using a near-surface relative density of 0.3. The dB/dt is from a recent model (Reference Ivins, James, Wahr, Schrama, Landerer and SimonIvins and others, 2013) of glacial isostatic adjustment. Combining terms in Eqn (3) gives
where dI/dt = dH/dt − dC
T/dt − dB/dt is an effective rate of ice thickness change taking into account the bedrock motion and the FC changes driven by temperature.
![]() combines direct height change and FC change which are both driven by accumulation variations.
combines direct height change and FC change which are both driven by accumulation variations.
The density associated with the dynamic-driven height changes is ρ i and the dynamic mass change for Eqn (1) is therefore
The accumulation-driven mass change is
where τ is the time period of the measurements. To clarify the timescales involved, dM
a/dt is determined only by δA(t) during τ, and not by prior anomalies or variations in V
fc. Secondly, variations in V
fc, which depend on the time history of T(t) and δA(t) before and during the measurements, only affect dC
T/dt and dC
A/dt. The values of dC
T/dt and dC
A/dt affect the apportionment of dI/dt = dH/dt − dC
T/dt − dB/dt between
![]() and dH
d/dt according to Eqn (4). Effects of δA(t) and T(t) variations before 1982 on the V
fc during 1992–2008 are shown to be limited to minimal values by the response times of the firn to A(t) and T(t) perturbations (Reference Li and ZwallyLi and Zwally, 2015).
and dH
d/dt according to Eqn (4). Effects of δA(t) and T(t) variations before 1982 on the V
fc during 1992–2008 are shown to be limited to minimal values by the response times of the firn to A(t) and T(t) perturbations (Reference Li and ZwallyLi and Zwally, 2015).
Our FC model is initiated with steady-state density profiles calculated for each gridcell (approximately 50 km 50 km) for thousands of years to convergence using estimates of long-term accumulation rate 〈A〉 and mean annual temperature 〈T〉. We use 〈A〉 modified from a compilation and interpolation of field data (Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000) and 〈T〉 as the average for 1982–84 of measured T(t) from satellite Advanced Very High Resolution Radiometer (AVHRR) measurements (Reference Li, Zwally and ComisoLi and others, 2007). From 1982 onward, the model is driven by monthly values of the measured T(t) and δA(t) from meteorological data. We use δA(t) = A(t) − 〈A(t)〉27, where A(t) is precipitation minus sublimation (P − S) from the European Centre for Medium-Range Weather Forecasts’ ERA-Interim atmospheric-model reanalysis (Reference DeeDee and others, 2011) and 〈A(t)〉27 is the 27 year average (1982–2008).
Most important for our purposes is the accuracy xof the temporal variability of δA(t). A comparison (Reference Bromwich and NicolasBromwich and Nicolas, 2011) of five reanalyses concluded that the ERA-Interim data provide the most realistic depiction of interannual variability and trends in Antarctic P − S during 1989–2009. Comparison of the time series of A(t) from the ERA-Interim data with the SMB from a regional atmospheric climate model (RACMO) (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012) shows an overall correlation of 0.79 over Antarctic grounded ice for 1979–2010, indicating similar overall temporal variability. However, comparison of the distributions of the dM a/dt we obtain using ERA-Interim (Section 4; Fig. 10, further below) with the distributions we obtain using RACMO shows significant differences in the spatial distribution of the temporal variability, particularly in coastal regions. We also find that both datasets give dM a/dt losses in EA for both measurement periods (−6 and −33 Gt a−1 for RACMO and −11 and −11 Gt a−1 for ERA-Interim). However, the large difference between periods suggested by the RACMO data gives a corresponding large difference in the dynamic thickening in EA, which we believe is not realistic.
Further support for our use of ERA-Interim is provided by a detailed analysis (Reference MedleyMedley and others, 2013) of the spatial and temporal correlations from 1980 through 2009 in WA between A(t) derived from layering shown by an airborne snow radar and (1) four reanalyses (including ERA-Interim and RACMO) and (2) ice cores. The snow radar flight lines covered ∼90 000 km2 of the eastern part of the 217 404 km2 of our DS21 extending slightly into DS22. The temporal correlation for ERA-Interim from 1980 through 2009 was 0.93 compared to only 0.68 for RACMO, 0.91 and 0.92 for the other two reanalyses and 0.80 for the ice cores. Furthermore, the time series of the snow radar data (fig. 3 of Reference MedleyMedley and others, 2013) shows a negative anomaly for 1992–2001 of −0.008 m w.e. a−1 versus a positive anomaly for 2003–08 of +0.024 m w.e. a−1. Assuming those anomalies extended over the entire DS21 gives net values of −1.6 and +5.1 Gt a−1 for the two periods, highly consistent with our respective dM a/dt of −1 ± 1 and +4 ± 2 Gt a−1 for DS21 using the ERA-Interim data. In contrast, our values for DS21 using RACMO are less satisfactory at −1 and +12 Gt a−1.
Regional values of the dH/dt, dC
T/dt, dI/dt,
![]() and dH
d/dt components of elevation change are shown in Table 2. Mean values over the AIS for the two measurement periods are dH/dt = 0.50 and 0.76 cm a−1; dC
T/dt = −0.30 and −0.27 cm a−1; dI/dt = 0.71 and 0.95 cm a−1;
and dH
d/dt components of elevation change are shown in Table 2. Mean values over the AIS for the two measurement periods are dH/dt = 0.50 and 0.76 cm a−1; dC
T/dt = −0.30 and −0.27 cm a−1; dI/dt = 0.71 and 0.95 cm a−1;
![]() and 0.27 cm a−1; and dH
d/dt = 1.20 and 0.69 cm a−1. For EA, the accumulation-driven
and 0.27 cm a−1; and dH
d/dt = 1.20 and 0.69 cm a−1. For EA, the accumulation-driven
![]() of −0.40 and −0.16 cm a−1 are small relative to the dynamic dH
d/dt = 1.58 and 1.59 cm a−1. The
of −0.40 and −0.16 cm a−1 are small relative to the dynamic dH
d/dt = 1.58 and 1.59 cm a−1. The
![]() are also small relative to dH
d/dt in WA1 and the AP where dynamic losses are large.
are also small relative to dH
d/dt in WA1 and the AP where dynamic losses are large.
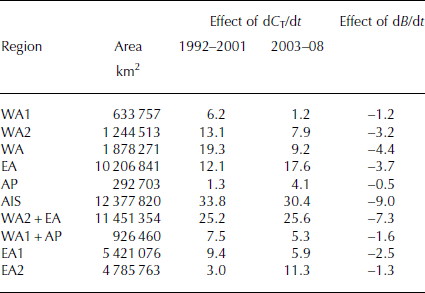
In EA, where dH/dt are 1.18 and 1.30 cm a−1 for the two periods, dC T/dt temperature-induced surface lowerings of −0.13 and −0.19 cm a−1 represent ∼10% corrections to the measured dH/dt. Applying those dC T/dt corrections to the measured dH/dt adjusts the derived dM/dt for EA by +12.1 and +17.6 Gt a−1 for the two periods as shown in Table 3. For WA, the respective temperature-induced corrections of 19.3 and 9.2 Gt a−1 are comparable to EA, because the temperature increases in WA are larger although their area is only 18% as large. For the AIS, the temperature-induced corrections are 33.8 and 30.4 Gt a−1, which emphasizes the importance of FC corrections for obtaining accurate mass-balance estimates during periods of climate warming (or cooling). As previously shown for Greenland (Reference Zwally and GiovinettoZwally and others, 2011), a 4.1 cm a−1 surface lowering induced by higher temperatures during 2003–07 might incorrectly be interpreted as a 54 Gt a−1 additional mass loss when the dC T/dt compaction is not taken into account.
Table 3. Mass effects (Gt a−1) of dC T/dt and dB/dt corrections on mass change estimates
4. Firn Densities (σ a) Associated with Accumulation-Driven dM a/dt and Pseudo-Densities Relating dH/dT to dM/dT
We also calculate the density, ρ
a, associated with dM
a/dt and the corresponding
![]() height changes using
height changes using
Although we do not use ρ
a with
![]() to calculate dM
a/dt as we did previously (Reference ZwallyZwally and others, 2011), the values of ρ
a are of interest because they represent the density of the firn added (or not added) as a result of the sum of the δA(t) anomalies over time . We use the regional average ρ
a in our estimation of errors, because the values of ρ
a affect how systematic errors in dM
a/dt cause corresponding systematic errors in dM
d/dt and dM/dt though their coupling in Eqns (1) and (4).
to calculate dM
a/dt as we did previously (Reference ZwallyZwally and others, 2011), the values of ρ
a are of interest because they represent the density of the firn added (or not added) as a result of the sum of the δA(t) anomalies over time . We use the regional average ρ
a in our estimation of errors, because the values of ρ
a affect how systematic errors in dM
a/dt cause corresponding systematic errors in dM
d/dt and dM/dt though their coupling in Eqns (1) and (4).
The ρ
a represent firn distributed over a range of depths depending on the temporal distribution of the δA(t) and how the anomalies propagate into the firn. Therefore, ρ
a do not represent the density of a particular firn layer at a specific depth. The distribution of ρ
a calculated for all gridcells over the AIS for the ERS and ICESat time periods is shown in the histograms of Figure 8. Realistic values of ρ
a cannot be calculated for all gridcells, because singularities occur when
![]() approaches zero causing unrealistically large positive or negative values of va. For the ERS and ICESat periods, 76% and 86% respectively of the ρ
a values lie between 0.2 and 0.92; the outliers are excluded from calculations of regional averages. The most probable ρ
a for the AIS is ∼0.33 in both periods. The average regional values of ρ
a range from 0.37 to 0.61, with an average of 0.39, over the AIS (Table 4). The average ρ
a is lowest at 0.37 in the colder EA where the compaction is slower, and is larger in the warmer areas at 0.46 in WA and 0.60 in the AP.
approaches zero causing unrealistically large positive or negative values of va. For the ERS and ICESat periods, 76% and 86% respectively of the ρ
a values lie between 0.2 and 0.92; the outliers are excluded from calculations of regional averages. The most probable ρ
a for the AIS is ∼0.33 in both periods. The average regional values of ρ
a range from 0.37 to 0.61, with an average of 0.39, over the AIS (Table 4). The average ρ
a is lowest at 0.37 in the colder EA where the compaction is slower, and is larger in the warmer areas at 0.46 in WA and 0.60 in the AP.

Fig. 8. Distribution of firn densities, ρ a, associated with dM a/dt accumulation-driven changes for AIS. In 1992–2001 (red) and 2003–08 (black), the average ρ a are 0.39 excluding outliers from singularities in Eqn (7).
Table 4. Accumulation density (ρ a), average density (ρ avg) and pseudo-densities (ρ pseudoH and (ρ pseudoI ) by region

In contrast to our calculation of dM
d/dt = ρ
i(dH
d/dt) using Eqn (5) with the well-defined ρ
i, use of
![]() to calculate the accumulation-driven mass change can only provide a rough approximation to dM
a/dt, because of the difficulties of calculating ρ
a. Furthermore, the local and regional values of dM
a/dt and dM
d/dt are highly variable and often of opposite signs, factors which preclude a priori selection of single or multiple densities to calculate dM/dt from measured dH/dt as has been done by several investigators. Examples are the selection of a single density (e.g. Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference ZwallyZwally and others, 2005) or binary densities depending on locations and assumptions about the dynamic or accumulation-driven character of the dH/dt (e.g. Reference SørensenSørensen and others, 2011; Reference ShepherdShepherd and others, 2012; Reference McMillanMcMillan and others, 2014). To further illustrate this issue, we consider several alternate definitions of densities. Reference Li and ZwallyLi and Zwally (2011) defined an average density as
to calculate the accumulation-driven mass change can only provide a rough approximation to dM
a/dt, because of the difficulties of calculating ρ
a. Furthermore, the local and regional values of dM
a/dt and dM
d/dt are highly variable and often of opposite signs, factors which preclude a priori selection of single or multiple densities to calculate dM/dt from measured dH/dt as has been done by several investigators. Examples are the selection of a single density (e.g. Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference ZwallyZwally and others, 2005) or binary densities depending on locations and assumptions about the dynamic or accumulation-driven character of the dH/dt (e.g. Reference SørensenSørensen and others, 2011; Reference ShepherdShepherd and others, 2012; Reference McMillanMcMillan and others, 2014). To further illustrate this issue, we consider several alternate definitions of densities. Reference Li and ZwallyLi and Zwally (2011) defined an average density as
![]() , which has values within the range of firn/ice densities (e.g. 0.80 and 0.86 in EA and 0.75 and 0.79 for the AIS; Table 4). However, there is no corresponding single dH/dt to use with ρ
avg to obtain the correct dM/dt. We also calculate ρ
pseudoH
dM/dt/(dh/dt × Area) and ρ
pseudoI
dM/dt/(dI/dt × Area) that give the correct dM/dt using our dM/dt, dH/dt and dI/dt from Tables 2 and 5. The values of the pseudo-densities vary widely as shown in Table 4 (e.g. maximal regional values of ρ
pseudoH
= 0.35 in 1992–2001 and 2.6 in 2003–08 in WA and 7.1 in 2003–08 in EA2, which are caused by local values of
, which has values within the range of firn/ice densities (e.g. 0.80 and 0.86 in EA and 0.75 and 0.79 for the AIS; Table 4). However, there is no corresponding single dH/dt to use with ρ
avg to obtain the correct dM/dt. We also calculate ρ
pseudoH
dM/dt/(dh/dt × Area) and ρ
pseudoI
dM/dt/(dI/dt × Area) that give the correct dM/dt using our dM/dt, dH/dt and dI/dt from Tables 2 and 5. The values of the pseudo-densities vary widely as shown in Table 4 (e.g. maximal regional values of ρ
pseudoH
= 0.35 in 1992–2001 and 2.6 in 2003–08 in WA and 7.1 in 2003–08 in EA2, which are caused by local values of
![]() and dH
d/dt that are in opposite directions). More reasonable values of ρ
pseudoH
in the range 0.86–1.8 are calculated separately for the WA1 and WA2 subregions of WA and for the whole of EA where
and dH
d/dt that are in opposite directions). More reasonable values of ρ
pseudoH
in the range 0.86–1.8 are calculated separately for the WA1 and WA2 subregions of WA and for the whole of EA where
![]() are small relative to dH
d/dt. The results for ρ
pseudoI
are similar to those for ρ
pseudoH
.
are small relative to dH
d/dt. The results for ρ
pseudoI
are similar to those for ρ
pseudoH
.
Table 5. Rates of total (dM/dt), dynamic-driven (dM d/dt) and accumulation-driven (dM a/dt) mass changes (Gt a−1) and surface mass balance (SMB) (Gt a−1) by drainage system (DS) and regions

In order to estimate dM/dt from either dH/dt or dI/dt, neither a single density nor binary densities dependent on location can properly account for the typical mixtures of accumulation-driven and dynamic-driven mass changes. The same problem applies to both the large areas of regions and sub-regions and to the smaller sizes of gridcells, as shown by the mixtures of accumulation-driven and dynamic-driven mass changes (often with opposite signs) at most locations in the maps of dM a/dt and dM d/dt (Figs 10 and 11). In particular, while the choice for relative ice density of 0.917 for the dynamically active portions of DS22, DS21, DS20, DS18 and DS13 (fig. 1 inset in Reference McMillanMcMillan and others, 2014) may seem appropriate, those areas also have significant dM a/dt for which McMillan and others snow density of 0.35 would be more appropriate. Furthermore, the spatial distribution of dM a/dt in those dynamically active areas changes with time as shown in Figure 10. More seriously, McMillan and others’ assignment of snow density to the rest of the AIS, in particular the very large areas of EA and WA2, with mostly dynamic thickening (Fig. 11) and small or negative dM a/dt (Fig. 10), causes underestimates of the mass gains.
5. Discussion of Results
Maps of the derived dM/dt, dM a/dt and dM d/dt for the two periods are presented in Figures 9–11, values by DS and defined regions are shown in Table 5, and values only by DS in Figure 12. For the whole of the AIS, mass gains from snow accumulation exceeded losses from ice discharge by 112 ± 61 and 82 ± 25 Gt a−1 respectively during the 1992–2001 and 2003–08 measurement periods. The overall positive balance is due to large net gains of +136 ± 50 and +136 ± 28 Gt a−1 in the two periods in EA, plus smaller net gains of +44 ± 14 and +72 ± 9 Gt a−1 in WA2. Those net gains together exceed the total losses of −60 ± 12 and –97 ± 6 Gt a−1 in WA1 and the losses of −9 ± 10 and –29 ± 2 Gt a−1 in the AP.

Fig. 9. Maps of total mass changes, dM/dt: (a) during 1992–2001 with overall positive balance of +112 ± 61 Gt a−1 (dH/dt from ICESat used south of 81.5°E); (b) during 2003–08 with +82 ± 25 Gt a−1. The distribution of dM d/dt in Figure 11 is very similar to dM/dt. In WA1, the mass-loss rate increased from 60 Gt a−1 to 97 Gt a−1 mainly due to a 51 Gt a−1 increase in dynamic thinning (note inland spreading of mass loss in 2003–08). In WA2 and EA together, the total mass gains of 180 and 208 Gt a−1 in the two periods are caused mainly by persistent dynamic thickening (deficiency of ice flow relative to long-term 〈A〉 ) of 202 and 211 Gt a−1, which is a residual of the dynamic response to a marked increase in precipitation at the beginning of the Holocene.

Fig. 10. Maps of the accumulation-driven mass changes, dM a/dt, during (a) 1992–2001 and (b) 2003–08. dM a/dt are generally smaller than dM d/dt (note 8× larger scale than in Figs 9 and 11). In WA1, the dM a/dt increase of 14 Gt a−1 in the 2003–08 period partially offset the 51 Gt a−1 increase in dynamic thinning. The increase in dM a/dt during 2003–08 also extended over DS23 and DS1, causing a 20 Gt a−1 increase in WA2, with negligible net changes in DS18 and DS19. In the AP (DS24–27), the dM a/dt variation is slightly positive during 1992–2001 and slightly negative during 2003–08. In EA, the variability of dM a/dt ranges from –8 Gt a−1 in DS12 during 1992–2001 and −9 Gt a−1 in DS14 during 2003–08 to +6 Gt a−1 in DS3 during 2003–08, but is unchanged at –11 Gt a−1 between periods over the whole of EA. (dM a/dt are calculated over the whole area.)

Fig. 11. Maps of the dynamic-driven mass changes, dM d/dt, (a) for 1992–2001 (dH/dt from ICESat used south of 81.5°E) and (b) for 2003–08. In WA1, the net dynamic-loss rate increased from 55 Gt a−1 to 106 Gt a−1. Dynamic thickening (excess of long-term accumulation over ice flux) occurred over WA2 and EA in both periods. Dynamic thickening (27 Gt a−1 in 2003–08) is strongest in DS18 in an area inland from Kamb Ice Stream that stagnated 150 years ago. Similarly, the dynamic thinning in Eastern DS17 and Western DS18 is inland of Mercer and Whillans Ice Streams, which restarted flowing 400 years ago.

Fig. 12. Rates of mass change and SMB by DS. (a) Total mass change and SMB, showing net mass losses in the AP and WA1 regions and gains in WA2 and EA. (b) Accumulation-driven mass change, showing the negative anomaly in WA1 and WA2 during 1992–2001 and the positive anomaly during 2003–08. (c) Dynamic-driven mass change, showing the increase in loss from dynamic thinning in the AP and WA1 and the gains from long-term dynamic thickening in WA2 and EA.
The indicated change of −29 ± 66 Gt a−1 between measurement periods in the overall AIS mass balance is not significant relative to the estimated uncertainties. In the EA region, dM/dt gains of 136 Gt a−1 in both periods also indicate no significant change (δ = 0 ± 57 Gt a−1), which is also true separately for the EA1 and EA2 subregions (δ = −7 ± 40 Gta−1 and +7 ± 33 Gt a−1). In contrast, regional changes in mass gains and mass losses in WA and the AP are significant. In WA2, the increase in mass gain from 44 ± 14 Gt a−1 to 72 ± 9 Gt a−1 (δ = +28 ± 16 Gt a−1) is statistically significant and is largely due to a 20 ± 8 Gt a−1 increase in dM a/dt from greater snowfall. Increases in mass loss in WA1 and the AP are also significant, and consistent with observations of accelerated mass loss in those regions (discussed below). Specifically in WA1, the mass loss increase is from −60 ± 12 Gt a−1 to −97 ± 6 Gt a−1 (δ = –37 ± 13 Gt a−1), and in the AP the mass loss increase is from −9 ± 10 Gt a−1 to −29 ± 2 Gt a−1 (δ = −20 ± 10 Gt a−1).
The dM a/dt maps (Fig. 10) illustrate the large spatial variability of accumulation in each period and the large temporal variability between periods. Regionally, dM a/dt increased by 14 ± 5 Gt a−1 in WA1 and by 20 ± 8 Gt a−1 in WA2 and decreased by 5 ± 2 Gt a−1 in the AP (Table 5). Although dM a/dt over EA is unchanged at −11 ± 6 Gt a−1 in both periods, it increased by 21 ± 8 Gt a−1 in EA1 and decreased by 21 ± 13 Gt a−1 in EA2, indicating a large regional shift in accumulation anomalies. In general, dM a/dt are small compared to dM d/dt. Overall, dM a/dt as a fraction of dM/dt are −21% and +6% for the two periods, whereas dM d/dt are much larger fractions at +121% and +95%.
In EA, the large dM/dt gains of 136 Gt a−1 in the two periods consist of dM d/dt gains of 147 Gt a−1 which are much larger than the small dM a/dt losses of 11 ± 6 and 11 ± 6 Gt a−1. The small losses from accumulation anomalies relative to the 27 year average accumulation show that the elevation increases and mass gain in EA are not caused by increasing snowfall during the 17 year measurement period. This result contradicts previous conclusions that growth in EA during the first period was driven by contemporaneous increases in snowfall (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005), a conclusion questioned by Reference MonaghanMonaghan and others (2006), or by accumulation variability and depth of the firn layer (Reference HelsenHelsen and others, 2008).
Instead, the dM/dt gains in EA are caused by a large dynamic thickening of 147 Gt a−1 due to a deficiency of ice flow relative to the long-term 〈A〉 (or equivalently an excess of 〈A〉 over the ice flow). Dynamic thickening extends over most of EA, and none of the DS have significant net dynamic thinning (i.e. <−6 ± 6 Gt a−1). DS13, which is close to dynamic balance in both periods due to near-coastal thinning on Totten Glacier, differs from the adjacent DS12 and DS14 which exhibit dynamic gains of 22 and 24 Gt a−1 and coastal thickening.
A dominant characteristic of the dynamic thickening in EA is its persistence, with no significant change between periods. This thickening is likely a result of the marked increase in accumulation that began in the early Holocene, ∼10 ka ago, with a 67–266% increase from the Last Glacial Maximum as derived from six ice cores (Reference SiegertSiegert, 2003). A residual thickening from the Holocene increase in accumulation is consistent with the characteristic slow response time of the ice flow to accumulation changes in EA. Comparing the 147 Gt a−1 dynamic gain with the SMB gives a current residual dynamic imbalance of ∼13%.
Using 100% as a rough estimate of the average accumulation increase in the early Holocene implies that the dynamic adjustment over the last 10 ka is ∼87% complete on average over EA. In the interior areas of the ice sheet, dynamic response times are much longer than in the higher-accumulation and thinner areas closer to the coastal margins. For example, in the interior of EA where the accumulation is low (e.g. 0.03 m a−1) and the ice is thick (e.g. 2500 m), the ice thickness increase over 10 ka is only ∼300 m. The corresponding fractional increase in driving stress over that time is only ∼12%, implying the flow takes a very long time to adjust to the change.
The WA2 portion of WA also exhibits a significant persistent dynamic thickening of ∼60 Gt a−1. Together, the combined dM d/dt of 202 and 211 Gt a−1 shows no significant short-term change. However, the timescale for some of the dynamic thickening in WA2 is shorter than the 10 ka thickening in EA based on other observations. Much of the 27 ± 2 Gt a−1 dynamic thickening in DS18 is inland of Kamb Ice Stream flowing into the Ross Ice Shelf, and is likely a result of ice-stream stagnation there ∼150 years ago (Reference Joughin, Tulaczyk, Bindschadler and PriceJoughin and others, 2002). Similarly, the dynamic thinning in the eastern part of DS17 and western part of DS18 is inland of Mercer and Whillans Ice Streams, which restarted flowing 400 years ago (Reference Hulbe and FahnestockHulbe and Fahnestock, 2007).
In contrast, WA1 shows a significant short-term increase in dynamic thinning from −55 ± 14 Gt a−1 to −106 ± 11 Gt a−1 (δ = −51 ± 17 Gt a−1). DS22, with ice discharge through Pine Island Glacier, has the largest increase in mass loss, from −8 ± 14 Gt a−1 to −35 ± 11 Gt a−1 (δ = −26 ± 9 Gt a−1), consistent with recent glacier acceleration (Reference Rignot, Vaughan, Schmeltz, Dupont and MacAyealRignot and others, 2002; Reference Wingham, Wallis and ShepherdWingham and others, 2009). The increased thinning in DS21 and DS22 extends >200 km inland from the front to the ice divide (Fig. 11). DS21, which discharges through Thwaites and Smith Glaciers, shows the largest dynamic thinning of any DS in Antarctica, increasing from −39 ± 6 Gt a−1 to –56 ± 5 Gt a−1 (δ = −16 ± 8 Gt a−1). DS20 shows a smaller increase in dynamic thinning of −8 ± 3 Gt a−1, which may be associated with the thinning of the Dotson and Getz Ice Shelves (Reference ZwallyZwally and others, 2005; Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van den Broeke and PadmanPritchard and others, 2012; Reference Paolo, Fricker and PadmanPaolo and others, 2015).
Much of the 51 ± 17 Gt a−1 increase in dynamic loss in WA1 is offset by a contemporaneous increase in snowfall of 34 ± 12 Gt a−1 in the whole of WA. The dM a/dt patterns in DS21 and DS22 of WA1 and DS23 and DS1 of WA2 differ between periods (Fig. 10), with a negative anomaly of 16 Gt a−1 during 1992–2001 and a positive anomaly of 20 Gt a−1 in 2003–08. For the whole of WA, the dM a/dt increase of 34 ± 12 Gt a−1 offset most of the −43 ± 37 Gt a−1 increase in dynamic thinning. In EA, snowfall anomalies subtracted 11 Gt a−1 from the total dM/dt in both periods. Over the whole AIS, accumulation anomalies reduced the balance by 24 Gt a−1 during 1992–2001 and added 5 Gt a−1 during 2003–08.
Between periods, the dynamic thinning in the AP increased by 15 ± 12 Gt a−1, which is consistent with (1) an increased loss (Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011) of 4.3 Gt a−1 from glacier acceleration and thinning in the Larsen B basin following ice-shelf disintegration in 2002, (2) a loss (Reference Shuman, Berthier and ScambosShuman and others, 2011) of 11.2 Gt a−1 in the Larsen A and B basins, (3) widespread acceleration of tidewater glaciers (Reference Pritchard and VaughanPritchard and Vaughan, 2007), and (4) extensive retreat of marine glacier fronts (Reference Cook, Fox, Vaughan and FerrignoCook and others, 2005).
As noted in Section 1, the evaluation of Reference ShepherdShepherd and others (2012) eliminated some larger estimates of Antarctic mass loss and gave a reconciled mean of −72 ± 43 Gt a−1 for the technique intercomparison period October 2003 to December 2008 (fig. 4 of Reference ShepherdShepherd and others, 2012). For WA, Shepherd and others’ reconciled mean of −67 ± 21 Gt a−1 contained the means and most of the ranges of the RA, LA, GR and IOM results from several research groups. Also, their reconciled mean of −28 ± 10 Gt a−1 for the AP contained the means and most of the ranges of the LA, GR and IOM results. In contrast, for EA the reconciled mean of +24 ± 36 Gt a−1 contained the means and most of the ranges of only the RA and GR results. The EA mean from IOM was more negative at −30 ± 76 Gt a−1 and the mean from LA was more positive at +109 ± 57 Gt a−1. Variations among the LA estimates were due to different methods of estimating dM/dt from dH/dt, differing choices for the ICESat inter-campaign biases, differing methods of dh/dt solutions, and different data-editing procedures, which have been improved for our EA mass gain of +136 ± 28 Gt a−1 in Table 5.
Possible causes for the lower RA estimate of +22 ± 39 Gt a−1 for EA are inadequate corrections to the Envisat data for variable radar penetration depth (as discussed in the Appendix) and the use of a low density of 0.35 to estimate dM/dt from dH/dt assuming the changes were due to snowfall anomalies (as discussed in Section 4). A likely cause for the lower GR estimate is the sensitivity of the GR estimates to the glacial isostatic adjustment (GIA) correction, as discussed in the Appendix where we note that a −1.6 mm a−1 change in the modeled dB/dt would bring the GR and our dM/dt into agreement at approximately +150 Gt a−1. The additional ice loading from a dynamic thickening of 1.59 cm a−1 over EA (Table 2) for 10 ka implies an additional bedrock depression of 27 m continuing at a rate of 2.65 mm a−1 assuming full long-term isostatic adjustment. Therefore, the −1.6 mm a−1 needed to bring the gravimetry and altimetry dM/dt estimates into agreement is only 60% of the full isostatic adjustment rate, and therefore within the range of what can be expected if the ice loading implied by the long-term dynamic thickening is accounted for in the GIA models.
A principal issue regarding the IOM concerns the extrapolation procedure used to estimate the ice discharge from non-observed areas, for which ice velocity measurements were not available, as shown in Reference Zwally and GiovinettoZwally and Giovinetto (2011) regarding the IOM results of Reference RignotRignot and others (2008, Reference Rignot, Velicogna, Van den Broeke, Monaghan and Lenaerts2011). The estimate in Reference RignotRignot and others (2008) for EA was near-zero at −4 ± 61 Gt a−1, which was based on an input estimate of 1131 Gt a−1, an observed output of 784 Gt a−1 and an extrapolated non-observed output of 349 Gt a−1. Therefore, a disproportionate 31% of Rignot and others’ total output from EA came from only 15% of the area that was non-observed. If the non-observed output had been scaled in proportion to the area as stated, then the non-observed output would be only 173 Gt a−1 (i.e. 15% from 15% of the area) and the net IOM balance would be +174 Gt a−1. Or if the non-observed slower-moving areas were only 70% as effective at discharging ice as the faster-moving observed areas, then the modified non-observed output would be +121 Gt a−1 and the net IOM balance estimate for EA would be +226 Gt a−1 (Reference Zwally and GiovinettoZwally and Giovinetto, 2011).
6. Conclusions
During the period 1992–2001, the Antarctic mass gain from snow accumulation exceeded the mass loss from ice discharge by 112 ± 61 Gt a−1. During 2003–08, the gain exceeded the loss by a similar 82 ± 25 Gt a−1, which is 4% of the SMB and equivalent to 0.23 mm a−1 sea-level depletion. The mass-balance distribution is mostly positive in EA and WA2, and mostly negative in the AP and WA1. Although the overall balance of the AIS shows no significant change over the 17 years, significant increases in the dynamic losses occurred from the AP and several coastal DS in WA; however, those increases in dynamic losses were partially compensated by accumulation increases in WA. In EA, no change occurred in the short-term contributions of short-term accumulation, which are slightly negative by 11 Gt a−1 in both periods compared to the 27 year average accumulation rate. Therefore, the positive mass balance in EA clearly has not been caused by contemporaneous increases in snowfall.
Major characteristics of the Antarctic imbalance are the large long-term dynamic thickening of 147 Gt a−1 in EA and 59 Gt a−1 in WA2, and the short-term increase of dynamic thinning from −55 Gt a−1 to −106 Gt a−1 in WA1 and from −9 Gt a−1 to −29 Gt a−1 in the AP. While continued increases in dynamic thinning are expected in response to thinning of adjacent ice shelves in WA1 and the AP (Reference Cook, Fox, Vaughan and FerrignoCook and others, 2005; Reference Pritchard and VaughanPritchard and Vaughan, 2007; Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011; Reference Shuman, Berthier and ScambosShuman and others, 2011; Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van den Broeke and PadmanPritchard and others, 2012), the long-term dynamic thickening in EA and WA2 should provide a significant buffer against such continued increases in mass loss. If dynamic thinning continues to increase at the same rate of 4 Gt a−2 with no offset from further increases in snowfall, the positive balance of the AIS will decrease from the recent 82 Gt a−1 to zero in ∼20 years. However, compensating increases in snowfall with climate warming may also be expected (Reference Gregory and HuybrechtsGregory and Huybrechts, 2006; Reference Winkelmann, Levermann, Martin and FrielerWinkelmann and others, 2012).
Acknowledgements
We thank D.H. Bromwich and J.P. Nicolas for assistance and advice on the reanalysis data, J.T.M. Lenaerts and M.R. van den Broeke for providing their SMB data for comparison, E. Ivins and P. Whitehouse for providing their GIA model results, A. Ridout for providing the Envisat SSH data, and S. Farrell for discussions about Arctic SSH measurements. In memoriam, we deeply appreciate the pioneering work of Seymour Laxon and Katharine Giles on measuring SSH in the Arctic from satellite altimetry. We also thank J. DiMarzio, D. Hancock and many others in the ICESat Project support group. This research was supported by NASA’s Project Science funding.
Appendix
ICESat inter-campaign biases
We use methods for determining the ICESat inter-campaign biases that have been used in the satellite-altimeter mapping of the level of open water and thin ice in leads and polynyas in sea ice by ICESat in the Antarctic (Reference Zwally, Yi, Kwok and ZhaoZwally and others, 2008) and the Arctic (Reference Farrell, Laxon, McAdoo, Yi and ZwallyFarrell and others, 2009), in the joint mapping by ICESat and Envisat of the mean dynamic topography in the Arctic Ocean (Reference FarrellFarrell and others, 2012), and in the analysis of temporal changes in the ocean dynamic topography observed by Envisat in the western Arctic Ocean (Reference Giles, Laxon, Ridout, Wingham and BaconGiles and others, 2012). Advantages of our method compared to other studies of campaign biases (Reference Urban and SchutzUrban and Schutz, 2005; Reference Hofton, Luthcke and BlairHofton and others, 2013; Reference Borsa, Moholdt, Fricker and BruntBorsa and others, 2014) include: (1) smooth surfaces in leads and polynyas that do not require a sea-state bias (significant wave-height) correction, (2) measured laser reflectivity of 0.42 that is closer to the 0.53 reflectivity of the adjacent sea ice and of ice sheets compared to the measured low reflectivity of 0.12 over open ocean, (3) availability of independent Envisat measurements of the vertical motion of the sea surface reference level, and (4) coverage over the reference surface by most of the laser tracks during each campaign.
We use the area of the Arctic Ocean that has sea-ice coverage with concentrations ≥20% in all ICESat campaigns up to the maximum latitude (81.5°N) of the Envisat radar altimeter coverage. In the Antarctic Ocean, we use the area that has sea-ice coverage with concentration ≥60% in all ICESat campaigns. Using previous methods (Reference Zwally, Yi, Kwok and ZhaoZwally and others, 2008), we calculate the average SSH measured by ICESat to open water and thin ice in leads and polynyas for each campaign period relative to a mean sea-surface reference. These ICESat measured values defined as D(t) include temporal variations in ocean dynamic topography as well as the regional sea-level rise. A positive (negative) D(t) bias indicates ICESat is measuring a higher (lower) SSH than the reference surface, and in either case subtracting the D(t) bias correction lowers (raises) the surface to which the D(t) is applied. We also calculate the average SSH measured by Envisat (defined as E SSH(t)) for the same areas and time periods using 10 day average mappings similar to Reference Giles, Laxon, Ridout, Wingham and BaconGiles and others (2012) that include the same temporal variations in SSH. We use the 10 day mappings of E SSH(t) that are within the time of the laser campaigns weighted by the number of days within the campaign.
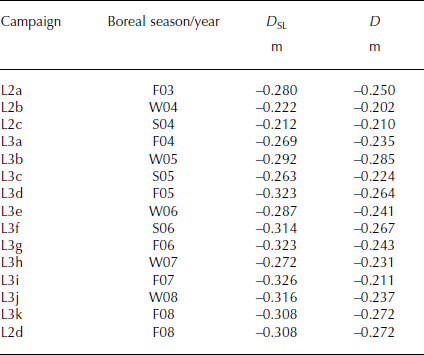
The resulting campaign biases corrected for concurrent changes in SSH are D SL(t) = D(t) − E SSH(t), which are determined separately over the Arctic and Antarctic sea ice and averaged as given in Table 6. We subtract the average D SL(t) for each laser campaign from the ICESat measured elevations at each laser footprint before calculating the along-track dh/dt, from which the dH/dt values are calculated. Although the time-dependent slope of D SL(t) can indicate the approximate effect of the bias corrections, it should not be used to calculate corrections to dh/dt or dH/dt values calculated without the bias corrections.
Table 6. ICESat laser campaign biases determined over leads and polynyas in sea ice. D SL are the ICESat-measured D corrected for changes in SSH measured concurrently by Envisat
ICESat Gaussian–centroid (G-C) range correction
As of December 2012, the ranges for ICESat/GLAS (Geoscience Laser Altimeter System) ice-sheet data products had been incorrectly calculated from the centroid (amplitude-weighted center of leading and trailing edge thresholds) of the transmit laser pulse to the center of a Gaussian fit of the return pulse (Reference ZwallyZwally, 2013). Applying the range correction for the transmit Gaussian to centroid (G-C) offset improved the range precision by 1.7 cm to <2 cm, and changed (but did not remove) the laser campaign biases (Reference ZwallyZwally, 2013). Our current analysis uses elevation data with the G-C correction applied and compatible bias corrections determined with data with the G-C correction also applied. Before the G-C correction was applied, the G-C offset had been in both the data for the ice-sheet dh/dt along-track solutions and in our bias calculations, so the effect of the offsets cancelled. We confirmed that cancellation by comparing our previous and current analyses of dH/dt. The average dH/dt for the AIS changed by only +0.01 cm a−1, and the average σ dH/dt error reduced from ±0.024 cm a−1 to ±0.012 cm a−1, reflecting the improved range accuracy. The corresponding dM/dt for the AIS changed by only +1 Gt a−1. Therefore, although the net effect of using ice-sheet data without the G-C correction applied is very small if commensurate bias corrections are applied, the error is significant (∼ −1.29 cm a−1) if the G-C correction is only applied to the data and not to the bias determinations (i.e. incorrectly causing a less positive or more negative dH/dt). The error is similar if the G-C correction is applied, but no inter-campaign bias adjustments are applied as in Reference Helm, Humbert and MillerHelm and others (2014) in which the volume change obtained from ICESat for 2003–09 for the AIS is consequently negative at −60 ± 44 km3 a−1. Similarly, ΔH i (i.e. ΔH(t i) in fig. 4 in Reference RichterRichter and others, 2014) mostly overlap rather than separate in time as they would if bias adjustments were applied. Also relevant is the discussion of residual errors after the G-C correction is applied and the need for inter-campaign bias adjustments in Reference Borsa, Moholdt, Fricker and BruntBorsa and others (2014).
Surface-based estimates of ice thickness and elevation changes
As noted in Reference Zwally and GiovinettoZwally and others (2005), estimates of ice thickness change were derived in the vicinity of Byrd Station (80°S, 120°W) in WA using two types of surface-based field measurements. The ice-flow and mass-continuity calculations using data from a 160 km surface-strain network extending northeast of the station gave an ice-thinning rate of 3 cm a−1 (Reference WhillansWhillans, 1977). GPS measurements on a pole in the firn with a fixed ‘coffee-can’ anchor point were combined with measurements of snow accumulation and downslope motion at a point near the station to give a surface lowering of 0.4 ± 2.2 cm a−1 (Reference Hamilton, Whillans and MorganHamilton and others, 1998). For comparison, Table 7 shows our dH/dt and the other components of elevation change for the 1992–2001 and 2003–08 periods interpolated to the locations of the surface measurements. For 1992–2001, the dH/dt surface lowerings at both locations are qualitatively consistent with the surface measurements within the errors, but much of that lowering is from a temperature-induced increase in firn compaction as shown by dC
T/dt. For 2003–08, a significant accumulation anomaly (cf. Fig. 10) as shown by the
![]() , which are 1–2 cm a−1 more positive than in the earlier period, contributed to the positive dH/dt at both locations, indicating the importance of accounting for accumulation variations. The derived values of dH
d/dt indicate essentially no dynamic thickening or thinning relative to the uncertainties, which reflects the location of Byrd near the ice divide with the strong dynamic thinning to the north in DS21 and DS22 and dynamic thickening to the south.
, which are 1–2 cm a−1 more positive than in the earlier period, contributed to the positive dH/dt at both locations, indicating the importance of accounting for accumulation variations. The derived values of dH
d/dt indicate essentially no dynamic thickening or thinning relative to the uncertainties, which reflects the location of Byrd near the ice divide with the strong dynamic thinning to the north in DS21 and DS22 and dynamic thickening to the south.
Table 7. Components of surface elevation change (cm a−1) at locations of surface measurements near Byrd Station

In light of our finding of a persistent spatially averaged positive dH/dt of 2.0 cm a−1 over Vostok Subglacial Lake during a 17 year period (Fig. 7), we review the estimates of surface height-change made using GPS measurements at locations on Vostok Subglacial Lake. Reference RichterRichter and others (2008) state, ‘we obtain the height change rate of the snow surface of +0.03 ± 0.49 cm a−1’ and ‘The height changes observed for the GPS markers [Table 1] reflect the vertical motion of the snow layer to which the markers are attached’. Reference RichterRichter and others (2014) state, ‘the height change rate was determined at +0.1 ± 0.5 cm/yr, indicating a stable surface height over the last decade’. However, our analysis of their adjustments for new snow growth around their GPS markers involves significant uncertainties that do not justify an interpretation of a near-zero rate of surface height change equivalent to the altimeter measurements.
First, their GPS ‘markers’ measure the downward velocity (V gps) of the GPS antennas on poles placed in the firn to some unspecified depths (fig. 2b in Reference RichterRichter and others, 2014). The measured V gps is intended to be the velocity of firn compaction plus the velocity of the ice beneath the firn. An unspecified potential source of error is possible motion of their GPS markers within the firn, because the poles do not have a well-defined anchor point as used, for example, by Reference Hamilton, Whillans and MorganHamilton and others (1998). Assuming that error is zero, Reference RichterRichter and others (2008) find V gps to be −6.21 cm a−1 for the average of seven markers in the vicinity of Vostok station in the southern part of the lake. However, to estimate the GPS-determined change in surface height (dh gps/dt), they needed to add the rise of the snow surface above the marker from new accumulation to their −6.21 cm a−1. A fundamental problem in Reference RichterRichter and others (2008) arises because they did not actually measure the rise of the snow surface in the vicinity of their GPS markers. Instead, they used an average accumulation rate, A (w.e.), along with a firn density of ρ ns =0.33 (for the upper 20cm of firn) to estimate the rate of rise from new accumulation as dS ns/dt = A/ρ ns.
However, dS ns/dt is not only sensitive to the choice of ρ ns for the near-surface snow/firn, but is even more sensitive to the choice of A by a factor of 1/ρ ns > 3. This is illustrated by Richter and others choice of a 200 year mean A = 2.06 cm w.e. a−1 from ice cores and pit measurements along with ρ ns = 0.33 to obtain dS ns/dt = 6.24 cm a−1, which added to V gps = −6.21 cm a−1 gives their dh gps/dt = +0.03 cm a−1. Alternatively, choosing ρ ns = 0.30 (probably a better value for the new near-surface snow than their ∼3 year 20 cm average) gives dS ns/dt = 6.87 cm a−1 and dh gps/dt = +0.66 cm a−1. Or if they had used their 1970–95 instrumental mean of A = 2.29 cm a−1 and ρ ns = 0.30, then dS ns/dt would have been 7.63 cm a−1 and dh gps/dt would be equal to +1.42 cm a−1. However, both of Richter and others’ A values are low compared to estimates from two compilations of field data and remote-sensing techniques, which give significantly larger dh gps/dt estimates. The alternate A are by (1) Reference Giovinetto and ZwallyGiovinetto and Zwally (2000), for which A = 3.0 cm a−1 in the vicinity of Vostok station and dh gps/dt = +3.79 cm a−1 (for ρ ns = 0.3); and (2) Reference Arthern, Winebrenner and VaughanArthern and others (2006), for which A = 3.7 cm a−1 and dh gps/dt = +6.12 cm a−1. Values of A in the range 2.4–3.0 cm a−1 are also supported by the 17 ka means along transects west of the lake derived from radar layering (Reference Vieli, Siegert and PayneVieli and others, 2004).
Therefore, alternate values to the dh gps/dt = 0.03 cm a−1 in Reference RichterRichter and others (2008) range from +1.42 cm a−1 (using their A = 2.29 cm a−1) to +6.12 cm a−1, which bracket our observed +2.02 cm a−1 by −30% to +200%. Using A = 2.47 cm a−1 (i.e. only 8% larger than their 1970–95 instrumental mean) would give dh gps/dt = +2.02 cm a−1, thereby matching our measurement.
In Reference RichterRichter and others (2008), instead of using an estimated dS ns/dt = A/ρ ns the authors state: ‘Applying the heights of the markers above the instantaneous local snow surface measured during the repeated GNSS [global navigation satellite systems] occupations we obtain a mean surface height change rate of +2 ± 4 mm a−1 for 41 markers within the floating part of the ice sheet. This value must be treated with caution, because the spatial sampling and observation time span are not sufficient to reliably determine the local snow buildup rate. Further the local accumulation conditions at the marker sites may be altered by anthropogenic activity during the GNSS occupations’.
ERS backscatter correction for variable penetration depth of radar signal in firn
For ERS-1 and -2 radar altimetry, we used an empirical backscatter correction (Reference ZwallyZwally and others, 2005; Reference Yi, Zwally, Cornejo, Barbieri and DiMarzioYi and others, 2011) to correct for the effects of variable penetration depth of the radar signal in the firn. Corrected elevation changes from the ERS radar altimetry were compatible with those from ICESat in Greenland (Reference Li and ZwallyZwally and others, 2011). From our analysis at Vostok Subglacial Lake (Fig. 7; Table 1), the dH/dt of the uncorrected ERS data is 2.18 cm a−1 and after the backscatter correction is 2.03 cm a−1, in close agreement with the ICESat dH/dt of 2.02 cm a−1. The seasonal amplitude of the H(t) from ERS also decreased significantly as the correction removed a strong seasonal variation in penetration depth. In marked contrast, the Envisat uncorrected dH/dt that we calculate is −7.6 cm a−1, and our corrected dH/dt of +0.2 cm a−1 does not agree with either the ERS or ICESat results. Our correction for Enivsat has a strong correlation with the direction of the surface slope with respect to the orientation of Envisat’s linearly polarized antennas, and some of the residual pattern related to surface slope remains in our backscatter-corrected Envisat dH/dt maps. The difficulties of correcting Envisat data for variable penetration depth are described further by Rémy and others (2012), wherein their along-track analysis (instead of crossover analysis) reduced the penetration errors because the antenna orientation relative to the direction of the surface slope was the same on successive tracks.
Bedrock motion correction
The regional values of the mass effects (Gt a−1) of the dB/dt from the model we use (Reference Ivins, James, Wahr, Schrama, Landerer and SimonIvins and others, 2013), another recent model (Reference Whitehouse, Bentley, Milne, King and ThomasWhitehouse and others, 2012) and our previous (Reference ZwallyZwally and others, 2005) average of three models (Reference Ivins, Wu, Raymond, Yoder, James and SiderisIvins and others, 2001; Reference HuybrechtsHuybrechts, 2002; Reference PeltierPeltier, 2004) are compared in Table 8. The effect of dB/dt, which is upward by an average of 0.12 cm a−1, is to reduce the dM/dt for the AIS by 8.7 Gt a−1. Regional reductions are 3.9 Gt a−1 in EA, 4.4 Gt a−1 in WA, and 0.5 Gt a−1 in the AP. Over the whole AIS, the dM/dt change from our previous estimate (Reference ZwallyZwally and others, 2005) caused by using the new model is significant (+53.3 Gt a−1), which accounts for much of the change from our previous net loss of 31 Gt a−1. The differences among these and other models are largest in EA, where the ice-loading/unloading history used in the models in poorly constrained (Reference HannaHanna and others, 2013). Also shown are the sensitivity to errors in dB/dt of the altimetry of 11 Gt mm−1 for the AIS compared to the Gravity Recovery and Climate Experiment (GRACE) gravity sensitivity of 68 Gt mm−1. For EA, the respective sensitivities are 9 and 56 Gt mm−1. The sensitivities are relatively small in WA and negligible in the AP, largely because of their smaller areas. The sensitivity for gravimetry is approximately six times larger than that for altimetry, which reflects the ratio of the density of mantle rock that affects the gravity to the density of ice that affects the altimetry.
Table 8. Values of −dB/dt (Gt a−1), correction to dM/dt for bedrock vertical motion
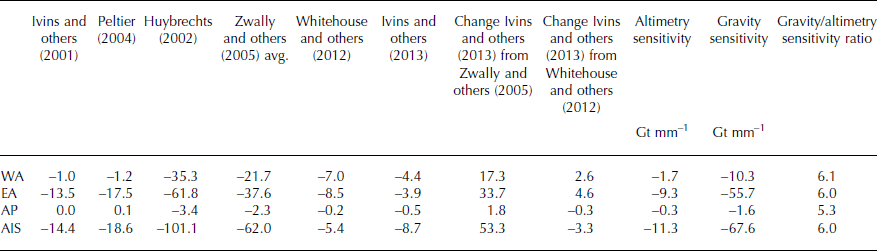
GIA model improvements have been a primary cause of AIS mass estimates from GRACE becoming less negative, and those for EA becoming more positive. Recent GRACE estimates of dM/dt for EA are +35 Gt a−1 (Reference ShepherdShepherd and others, 2012), +60.2 ± 12.8 Gt a−1 (Reference Whitehouse, Bentley, Milne, King and ThomasKing and others, 2012) and 62.8 ± 28.1 Gt a−1 (Reference Hofton, Luthcke and BlairLuthcke and others, 2013). Additional convergence may occur as the full implications of long-term growth of EA are taken into account in the ice-loading history. Considering the relative sensitivities of gravity and altimetry to dB/dt (Table 8), a change in the modeled dB/dt for EA downward by 1.6 mm a−1 (from the small average uplift of +0.4 mm a−1 (Table 2) to −1.2 mm a−1) would bring the two GRACE-based dM/dt estimates of 60.2 ± 12.8 Gt a−1 and 62.8 ± 28.1 Gt a−1 in line with a corresponding adjustment of our ICESat value of 136 ± 28 Gt a−1 at ∼150 Gt a−1 for both methods.
The small modeled uplift of +0.4 mm a−1 averaged over EA implies a history of ice unloading used in the GIA model. The ice-loading histories typically treated in the models are episodic ice unloadings during a glacial–interglacial transition, which cause relatively rapid isostatic adjustments, followed by a much slower residual response rate decaying over thousands of years. In contrast, our finding of a stable dynamic thickening of 1.59 cm a−1 over EA (Table 2), along with our interpretation as long-term dynamic thickening for 10 ka since the early Holocene, implies a slow long-term ice loading resulting in the addition of 159 m of ice averaged over EA in 10 ka. Using 6 for the ratio of the density of mantle rock to the density of ice implies an additional bedrock depression of 27 m continuing at a rate of −2.65 mm a−1 assuming full long-term isostatic adjustment. Therefore, the −1.6 mm a−1 needed to bring the gravity and altimetry dM/dt estimates into agreement is only 60% of the full isostatic adjustment rate, and therefore within the range of what can be expected if the ice loading implied by the long-term dynamic thickening is accounted for in GIA models.
Estimates of uncertainties
Our uncertainty estimates include a combination of random and systematic errors. The random errors are calculated first for each gridcell and then for the sums over DS and regions. The systematic errors are applied to the sums over DS and regions. The random errors σ cell(dH d/dt) on the dynamic-driven height change, which is given by Eqn (3), are calculated for each gridcell using

where the terms in Eqn (3) and the corresponding errors are for averages over each gridcell. The respective errors used are: (1) σ
dH/dt
is the sigma of the average of the dh/dt in each gridcell using the formal σ
dh/dt
from along-track solutions of dh/dt for ICESat (Reference Li and ZwallyZwally and others, 2011) and using the sigma of the slope of the time-series analysis of crossover differences for ERS (Reference ZwallyZwally and others, 2005); (2)
![]() is the sigma of the cell dC
T/dt linear fit of the FC solution; (3) σ
dB/dt
is ± 50% on the cell dB/dt; and (4)
is the sigma of the cell dC
T/dt linear fit of the FC solution; (3) σ
dB/dt
is ± 50% on the cell dB/dt; and (4)
![]() is ±30% on each cell
is ±30% on each cell
![]() also from the FC solution. The random cell error on dM
d/dt is σ
cell(dM
d/dt) = ρ
ice
σ
cell(dH
d/dt)A
cell, where A
cell is the area of the cell adjusted for the partial-cell fraction of the cell at the ice edges and DS boundaries. The random error on dM
a/dt is taken to be σ
cell(dM
a/dt) = 0.30dM
a/dt (i.e. 30% of the cell dM
a/dt). The random error on dM/dt is then
also from the FC solution. The random cell error on dM
d/dt is σ
cell(dM
d/dt) = ρ
ice
σ
cell(dH
d/dt)A
cell, where A
cell is the area of the cell adjusted for the partial-cell fraction of the cell at the ice edges and DS boundaries. The random error on dM
a/dt is taken to be σ
cell(dM
a/dt) = 0.30dM
a/dt (i.e. 30% of the cell dM
a/dt). The random error on dM/dt is then
The values of dM/dt, dM a/dt and dM d/dt for DS, the regions and the AIS are obtained by summation of the cell values in the respective areas. The corresponding standard errors of the sums [σ sum(dM/dt), σ sum(dM a/dt) and σ sum(dM d/dt)] are calculated with the standard calculation (i.e. square root of the sum of the squares of σ cell).
We then add systematic errors to the DS and regional values of dM/dt, dM a/dt and dM d/dt that are intended to be similar to 1σ estimates and are signed ± similar to the random errors. The assigned systematic errors in height are the following: 1σ is a calibration error taken to be ±0.20 cm a−1 for ERS and ±0.15 cm a−1 for ICESat; σ 2 is a bedrock motion error taken to be the difference between the dB/dt from the GIA models of Reference Ivins, James, Wahr, Schrama, Landerer and SimonIvins and others (2013) and Reference Whitehouse, Bentley, Milne, King and ThomasWhitehouse and others (2012); σ 3 is an additional spatial interpolation error for ERS, taken to be ±5% of the dh/dt plus the height equivalent of ±2 Gt a−1 in both DS25 and DS26 and ±5 Gt a−1 for the AP; and σ 4 is an estimate of the error in backscatter correction for variable radar penetration depth of ERS taken to be ±5% of dH/dt. The systematic σ 1, σ 2, σ 3 and σ 4 are added to the random σ sum(dM/dt) and to σ sum(dM d/dt) in Eqns (A4) and (A5), but they do not affect the σ sum(dM a/dt).
A systematic error σ system(dM a/dt) equal to ±50% of dM a/dt is added to the random error on dM a/dt, giving the total error on the accumulation-driven mass changes:
The σ
system(dM
a/dt) cause corresponding systematic errors in dM
d/dt and dM/dt through their coupling in Eqns (1) and (3). For example, a positive error of +ε in dM
a/dt, caused by an accumulation anomaly with an associated height change of approximately
![]() , causes corresponding errors of |−ε(ρ
ice /ρ
a)| in σ(dM
d/dt) and |ε(1 −ρ
ice/ρ
a)| in σ(dM/dt). We use average values of ρ
a for each region from Table 4 that range from 0.37 to 0.61, giving ρ
ice/ρ
a ratios from 2.46 to 1.49 for the relative effect on σ(dM
d/dt) and (ρ
ice/ρ
a − 1) ratios from 1.46 to 0.49 for the smaller effect on σ(dM/dt). Average values of ρ
a over each DS are used to calculate the errors by DS.
, causes corresponding errors of |−ε(ρ
ice /ρ
a)| in σ(dM
d/dt) and |ε(1 −ρ
ice/ρ
a)| in σ(dM/dt). We use average values of ρ
a for each region from Table 4 that range from 0.37 to 0.61, giving ρ
ice/ρ
a ratios from 2.46 to 1.49 for the relative effect on σ(dM
d/dt) and (ρ
ice/ρ
a − 1) ratios from 1.46 to 0.49 for the smaller effect on σ(dM/dt). Average values of ρ
a over each DS are used to calculate the errors by DS.
These errors on dM a/dt have the effect of making most of the σ(dM d/dt) larger than σ(dM/dt), because their random and other systematic errors are similar. The total error on the dynamic mass changes is

where A DS or Reg is the area of the DS or region. The total error on the total mass change is

























