1. Introduction
Being able to predict the evolution of glaciers around the world using numerical models is a key requirement in constraining future sea-level rise. However, these models require a priori information about the glaciers, such as surface topography and velocities (the latter particularly for calibration or validation). These surface variables are relatively easy to observe, with various satellite remote-sensing platforms providing near-global coverage at temporal resolutions of a few days or weeks, but accurate volume quantification and prediction in a model also requires information on the glacier bed. On many glaciers, especially small mountain glaciers, this information may be completely nonexistent or only available in the form of sparse observations (the motivation behind the ITMIX project, see Farinotti and others, Reference Farinotti2017), such as a single flight-line or a collection of boreholes, yet the topography of the bed has been shown to be crucial in determining the fate of large, tidewater outlet glaciers, and thus their evolution and the resulting sea-level rise (e.g. Csatho and others, Reference Csatho2014; Morlighem and others, Reference Morlighem2017; Felikson and others, Reference Felikson, Catania, Bartholomaus, Morlighem and Noël2020; An and others, Reference An2021).
Several techniques exist to overcome these limitations and provide continuous bed DEMs for model input, such as straightforward interpolation or kriging (e.g. Morlighem and others, Reference Morlighem2017), and mass conservation (e.g. Morlighem and others, Reference Morlighem2017) in cases where some information exists, or the use of the plastic flow assumption (e.g. Haeberli and Hoelzle, Reference Haeberli and Hoelzle1995) and the shallow ice approximation (SIA) (e.g. Farinotti and others, Reference Farinotti2017; Millan and others, Reference Millan, Mouginot, Rabatel and Morlighem2022) to infer the bed from surface characteristics where no bed information exists. However, these techniques all have limitations: simple interpolation fails to conserve mass, mass conservation is only accurate in areas of high velocity, the SIA is conversely less effective as velocities increase, and the plastic flow assumption is an empirical law that may not be suitable for a given individual glacier (see Farinotti and others, Reference Farinotti2017, Reference Farinotti2021 for discussion of methods for reconstructing glacier thickness). It is unsurprising therefore that global glacier volume and its evolution remain subject to substantial uncertainty, and that future sea-level rise is also inherently uncertain (e.g. Stocker and others, Reference Stocker2013).
Data-assimilation techniques have increasingly been used to try to resolve these problems (e.g. Larour and others, Reference Larour2014; Sergienko and others, Reference Sergienko, Creyts and Hindmarsh2014; Shapero and others, Reference Shapero, Joughin, Poinar, Morlighem and Gillet-Chaulet2016; Maier and others, Reference Maier, Gimbert, Gillet-Chaulet and Gilbert2021). These have typically taken the form of a static, ad hoc inversion for unknown basal properties through minimising a cost function that relates observed surface variables (usually, in glaciology, ice surface elevation and/or ice surface velocity) to their modelled equivalents. This has the disadvantage of only providing a constant field for the inverted parameter (often a quantity representing basal friction in some form) based on a particular temporal snapshot of an unrealistic, unrelaxed glacier, which, given glaciers evolve through time, is also likely to become increasingly inaccurate as the model moves away from the time at which the inversion was performed. The inversion is also only valid for the model's version of the glacier. Due to data-availability constraints, the understandable combination of datasets gathered over different periods by different sensors (Landsat, Sentinel, MODIS, etc.) to construct the model glacier may, once relaxation has occurred and model artefacts removed, lead to a glacier with substantial geometric differences to its real-life equivalent that will then feed through into any inversion performed. Therefore, the inverted parameter field may not necessarily provide useful information on the real parameter field.
One technique that may help to resolve these issues – inversions based on temporally mismatched datasets, geometric differences between modelled and real glaciers, among others – is the use of transient data assimilation in glaciological models. There are two main approaches for doing this: using an ensemble Kalman filter (e.g. Bonan and others, Reference Bonan, Nodet, Ritz and Peyaud2014, Reference Bonan, Nichols, Baines and Partridge2017; Gillet-Chaulet, Reference Gillet-Chaulet2020), whereby more readily available surface observations, as well as any bed observations, are integrated into the numerical model to iteratively correct the model state towards one representing the ‘real’ glacier. The model is run transiently across an ensemble of members that are provided with a range of possible beds derived, for example, using one of the techniques mentioned above (cf. Gillet-Chaulet in Farinotti and others, Reference Farinotti2021), representing the uncertainty on the position of the actual bed. As observations are integrated at the appropriate time in the assimilation period, the ensemble members should converge towards the actual bed. An alternative data-assimilation approach is provided by the use of the more complex time-dependent 4DVar technique (e.g. Goldberg and Holland, Reference Goldberg and Holland2022), where the forward model instead runs iteratively over the assimilation period, attempting to minimise a cost function describing the misfit between the model and all available observations. Regardless of the exact approach taken, the end point of a data-assimilation process should ultimately be a self-consistent model that closely resembles its real equivalent (Carrassi and others, Reference Carrassi, Bocquet, Bertino and Evensen2018), with (in the case of the Kalman-filter approach) the mean bed calculated across all the ensemble members being the best possible approximation of the actual bed. It is also worth noting that data assimilation consequently provides an interesting alternative to traditional model spin-up and relaxation, which can lead to model glaciers divergent from their real-world equivalents, and is further capable of quantifying the degree of uncertainty in the model by looking at the spread of the ensemble.
Data assimilation using an ensemble Kalman filter is a relatively new tool in glaciological modelling and has previously been applied with some success to 2D flowline models of synthetic ice sheets using the shallow shelf approximation (Gillet-Chaulet, Reference Gillet-Chaulet2020) and a data-assimilation model was one of those that took part in the second phase of the ITMIX model intercomparison project (Farinotti and others, Reference Farinotti2021). This paper, building on this work, therefore presents a set of 25 2D flowline data-assimilation experiments conducted on a semi-synthetic mountain-glacier model domain using the Elmer/Ice flow model (Gagliardini and others, Reference Gagliardini2013) to test the performance of data assimilation in reconstructing glacier beds in a range of scenarios.
2. Method
The 25 simulations for this paper were run using Elmer/Ice (Gagliardini and others, Reference Gagliardini2013) as the forward model and PDAF v1.15 (Nerger and Hiller, Reference Nerger and Hiller2013; Nerger and others, Reference Nerger, Tang and Mu2020), an open-source library for ensemble data-assimilation applications, for the assimilation. The two components are coupled in an offline mode. Following Gillet-Chaulet (Reference Gillet-Chaulet2020), we use the local version of the error subspace ensemble transform Kalman (ESTKF) filter implemented in PDAF. Section 2.1 provides a brief summary of data assimilation and the ESTKF, Section 2.2 describes model set-up, including the glacier geometry we used for the simulation and the derivation of the initial beds for the model ensembles, and Section 2.3 gives details on the individual simulations.
2.1. Data assimilation and the ESTKF
2.1.1. Initial states
A key challenge in using ensemble modelling is generating the correct initial states for the ensemble. The range of initial states of the ensemble members should correspond to the error space attached to the parameter(s) that the assimilation is attempting to reconstruct (here, the glacier bed); these initial states also need to reflect spatial correlations in the errors associated with these parameters (if existing observations are sufficient to provide information on this), so generating them using uncorrelated white noise is inappropriate. Data assimilation using ensemble Kalman filters has typically previously been used prognostically in meteorological modelling applications (see the review paper by Carrassi and others, Reference Carrassi, Bocquet, Bertino and Evensen2018, for an overview of past use of data assimilation and ensemble Kalman filters within the geosciences), where these initial states are instead provided by an existing previous climatology from manifold observations and simulations, sometimes supplemented by a covariance model. This is, however, impossible in glaciological applications, such as this one, where the initial state of the parameter is often unknown (cf. Millan and others, Reference Millan, Mouginot, Rabatel and Morlighem2022), hence requires more consideration than in other geophysical applications of the method.
One possible solution to this initialisation problem in a glaciological context was provided by the ITMIX experiments (Farinotti and others, Reference Farinotti2017, Reference Farinotti2021), where, in Phase 1, an ensemble of glacier thickness models using a variety of reconstruction techniques (as described in Section 1) attempted to reconstruct a set of known glacier beds based on defined sets of observations. The results of this showed that the ensemble of models was unbiased and that the mean bed across all the models was actually a good approximation of the real glacier bed. The ensemble of beds this created was then used as the initial bed input to a data-assimilation model that took part in Phase 2, which further showed that (a) data assimilation using this input performed well and (b) that this initial ensemble gave a good representation of the uncertainty on the true bed locations. Of course, running several different thickness-reconstruction models for a glacier may be computationally complicated, but ITMIX does suggest this is a worthwhile direction to explore as a way of generating good initial bed states for an assimilation-based ensemble approach. However, many of the approaches used are only 1D, which may pose problems in more complex glacial environments, something that would require further development.
2.1.2. Model procedure
Employing data assimilation and an ensemble Kalman filter (of which the ESTKF is a kind) requires two distinct components: a forward step and an analysis step. These occur multiple times within the overall assimilation period, which is the period over which observations are available and, at the end of which, a self-consistent model glacier that closely resembles its real equivalent at the same point in time is to be obtained, which can then be used as the starting point for prognostic simulations. In each forward step, the forward model (here, Elmer/Ice) is run until time t, when the next set of observations to be assimilated are available. When t is reached, an analysis step is performed, which updates the ensemble states with the new information, modifying the trajectory of the forward model to one closer to the real-life system. Over several forward-analysis iterations, the ensemble members become increasingly constrained and the mean state and trajectory of the system should converge towards the real state and trajectory.
2.1.3. Further considerations
However, the number of ensemble members required to fully explore the error space of the parameter(s) is prohibitively large in terms of computing resources and would also increase the difficulty of the analysis step, hence our use of the ESTKF, which allows us to conduct the analysis step within a much smaller error subspace, making the problem far more tractable. Using an error subspace, though, does require us to consider inflation and localisation parameters to overcome problems related to under-sampling; investigating appropriate values for these parameters is one of the objectives of this paper. The inflation parameter defines an ad hoc multiplier applied to the forecast covariance matrix to directly counter the rank deficiency of the covariance matrix. In other words, the inflation factor in some sense creates virtual ensemble members that stop the ensemble spread from becoming too small and the analysis becoming over-confident. It is worth noting that, following Gillet-Chaulet (Reference Gillet-Chaulet2020), our inflation factor is a forgetting factor, with a value of 1 denoting no inflation and inflation then increasing towards the lower limit of 0. The localisation parameter, meanwhile, is a solution to the problem of nonphysical long-distance correlations in the system introduced by this same rank deficiency. The parameter therefore gives the radius (in m, in this study) around each model node to search for observations, limiting the analysis to observations that are most likely to influence that node and filtering out distant observations. At the same time, because the analysis at each node is thus using a different set of observations, localisation also implicitly increases the rank of the covariance matrix.
For further details and a full mathematical treatment of the ESTKF, the reader is directed to Nerger and others (Reference Nerger, Janjić, Schröter and Hiller2012); and for its application in a glaciological context to Gillet-Chaulet (Reference Gillet-Chaulet2020). For data assimilation in the geosciences more broadly, the recent review paper by Carrassi and others (Reference Carrassi, Bocquet, Bertino and Evensen2018) is a good starting point. For different methods of reconstructing glacier beds more broadly, the results of phases 1 and 2 of the ITMIX experiment (Farinotti and others, Reference Farinotti2017; Reference Farinotti2021) provide a good overview.
2.2. Model set-up
We performed a twin experiment following Gillet-Chaulet (Reference Gillet-Chaulet2020). The initial glacier bed was taken from the Haut Glacier d'Arolla dataset used as an input for part of the Ice Sheet Model Intercomparison Project for Higher-Order ice sheet Models (ISMIP-HOM) (Pattyn and others, Reference Pattyn2008). Using a simple surface-mass-balance (SMB) function with the equilibrium line altitude (ELA) set to 2800 m, we allowed a glacier to grow on this bed until a steady state was reached after 800 years. From this semi-synthetic glacier, we ran a reference 2D flowline Stokes simulation for a period of 100 years, where the ELA was moved to 2900 m, leading to glacier retreat. A no-slip condition was imposed on the glacier bed and ice temperature was set to a constant −3.0°C. Ice velocity was set to zero at the inflow boundary; no conditions were imposed on the other boundaries. The 25 2D ensemble simulations used these same parameters and boundary conditions.
The observations to be assimilated (surface velocity and elevation) were taken from the reference simulation with white noise added (2 m a−1 for velocity; 10 m for elevation except where specifically noted in Section 2.3); the exact set-up for each simulation is explained further in Section 2.3. The analysis steps then use these observations to correct our prognostic variable (surface elevation) and our parameter of interest (bed elevation). The model domain is approximately 5 km in the x direction and 0.7 km in the y direction with resolution varying from 25 m near the glacier front to 50 m at the headwall. This gives 153 surface nodes on which the observations and parameters are defined and assimilated.
The initial ensemble beds (Fig. 1), except where specifically noted in Section 2.3, were devised using the same approach as set out in Gillet-Chaulet (Reference Gillet-Chaulet2020), i.e. drawn from conditional Gaussian simulations based on a variogram of the bed derived from the reference bed and an exponential variogram model. The bed observations for input to the variogram were taken at random x-axis locations from the ISMIP-HOM Arolla data at, on average, 500 m intervals (the PlasticBed simulation, described below, Section 2.3.4, explores what happens if we are less generous with our initial bed observations), and the variogram sill was set to 200 m, range to 4900 m, and a nugget of 100 m was added to ensure sufficient uncertainty. Using this variogram approach ensures that spatial correlations in the bed topography are preserved in the ensemble members. It may also be remarked that the variogram approach leads to, in this case, the ensemble beds being biased low at the very top of the glacier (Fig. 1), as no observations were included here in the random draw of x-axis locations, forcing the function to extrapolate. This feature is corrected after a few analysis steps, however. It is also necessary to note that numerical problems with the free surface solver are responsible for the sawtooth surface near the front of the glacier. These have no impact on model functioning, but are an unrealistic feature.

Figure 1. The mean initial ensemble bed. The black line shows the reference bed, the dotted black line shows the initial surface, the red line shows the mean ensemble bed, the blue area shows the ensemble range, and the shading shows the glacier velocity.
A prognostic run of 100 years was also conducted using the initial mean ensemble bed and without assimilation of any kind to provide a reference maximum error. At the end of the simulation the volume of this no-assimilation modelled glacier had diverged by 5% from the reference simulation, with a bed root-mean-square error (RMSE) of 25.25 m and a surface RMSE of 14.65 m when compared with the reference simulation.
2.3. Simulations
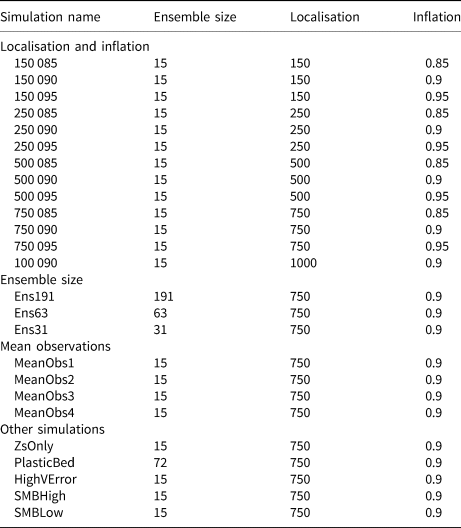
Important characteristics for all simulations are summarised in Table 1.
Table 1. Summary of simulations detailing ensemble sizes, and localisation and inflation parameters used for each simulation
2.3.1. Localisation and inflation
The first 13 simulations test a range of inflation and localisation parameters for a 15-member ensemble (all combinations of localisation radii of 150, 250, 500 and 750 m, and inflation parameters of 0.85, 0.9 and 0.95, with one further run of localisation radius 1000 m and inflation of 0.9). The first 25 years of observations from the reference simulation were assimilated on a year-by-year basis, then the forward model was left to run for a further 75 years. All other simulations then used the best inflation and localisation parameters determined from these simulations.
2.3.2. Ensemble size
These three simulations followed the same experimental protocol as described in Section 2.3.1, above, but tested larger ensemble sizes to see if these produced significant improvements in model performance.
2.3.3. Mean observations
These four simulations tested the performance of repeatedly assimilating only one set of observations to test the likely real situation where this may be the case (and is indeed the artificially imposed case in ITMIX (Farinotti and others, Reference Farinotti2017)). Many glaciers do not have long time series of observations, hence the decision in ITMIX to only provide one set of observations, and our decision to replicate this context in this study.
By imposing the apparent SMB (actual SMB minus the elevation change over time, dh/dt) rather than the actual SMB, we assume the glacier is in a steady state and that surface observations should therefore not change. To avoid overfitting the errors in the surface observations, we add a different white noise field of the same standard deviation as the error to the observations at each analysis step, allowing the assimilation process to extract as much information as possible from the underlying initial set. In this case, the assimilation essentially iterates towards a steady state defined by the glacier state at the time the single set of observations was gathered, rather than being, conceptually, a single transient run of increasing accuracy. This is similar to the approach taken by Brinckerhoff-v2 in ITMIX (Farinotti and others, Reference Farinotti2017), where they used a Stokes flow model and apparent SMB to attempt to reconstruct the bed, but through the minimisation of an ad hoc cost function linked to the error between the modelled and observed glacier surface.
MeanObs1 and MeanObs2 used the observations from t = 25; MeanObs3 and MeanObs4 used the mean observations from t = 21 to t = 25. All four experiments used observations with a new white noise field applied at each assimilation step, and subtracted dh/dt for the period t = 24–25 from their SMB function with the aim of replicating the reference glacier state at t = 25. MeanObs1 and MeanObs3 ran each forward-model step until a steady state was reached (50–75 years); MeanObs2 and MeanObs4 only ran each forward-model step for 10 years. In all cases, as many forward steps as necessary were run to reach a point where the RMSE between the mean ensemble bed and the reference bed ceased decreasing; the forward model was then run for a further 75 years for comparison with the other simulations.
2.3.4. Other simulations
Five further simulations were run to test other aspects of the assimilation model. These all used the same experimental protocol as described in Section 2.3.1, except as listed here. ZsOnly used only surface elevation observations in its assimilation to replicate a case where no surface velocity data were available, for example on slow-flowing, smaller glaciers. PlasticBed used an ensemble with beds constructed using the plastic flow assumption (Haeberli and Hoelzle, Reference Haeberli and Hoelzle1995), with variation of the parameters within this giving the 72-member ensemble used, in order to replicate a situation where no observations of the bed exist (see Section 2.1.1), as is the case for 98% of the world's glaciers (Millan and others 2002). The relevant equations are:
Where τf is the basal shear stress along the central flowline, f is a shape factor, ρ is the ice density, g is the gravitational constant, hf is the ice thickness along the central flowline, α is the surface slope and ΔH is the difference between the maximum and minimum glacier surface elevation. α is calculated separately for the ablation and accumulation areas using:
Where L0 is the length of the glacier in the accumulation area and La is the length of the glacier in the ablation area. We vary La ( = 0.5, 0.55, 0.6, 0.65, 0.7, 0.75), f ( = 0.4, 0.6, 0.8, 1.0) and the constant in Eqn 2 ( = 0.005, 0.025, 0.045).
HighVError assigned a higher and more realistic error of 10 m a−1 to the velocity observations to test the performance of assimilation even with poor-quality velocity data (maximum modelled velocities are on the order of 10 m a−1, so this error represents a signal-to-noise ratio of ≈1 or higher). SMBHigh and SMBLow, respectively, increased and decreased the gradient in the SMB function used by 10% to evaluate the impact of erroneous SMB data.
3. Results
Key results from all simulations are shown in Fig. 2 and Table 2. Each group of simulations is considered further in the relevant sub-section (3.1–3.4).
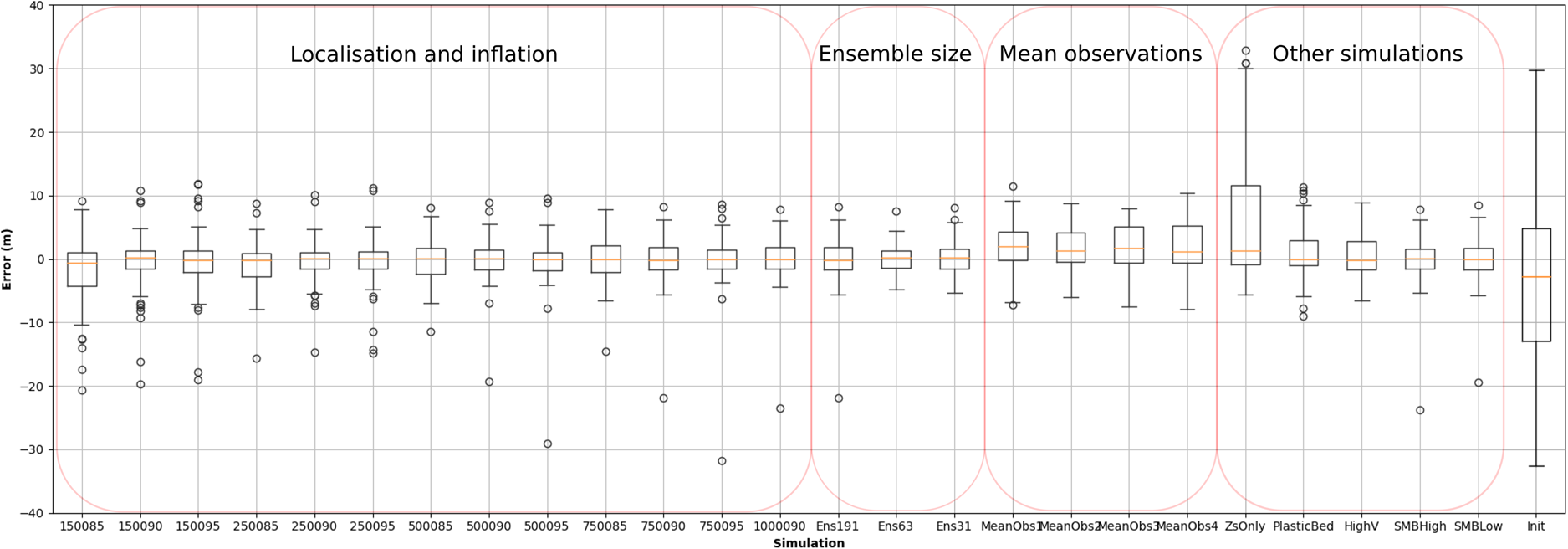
Figure 2. Box plot of errors between the mean ensemble bed and the reference bed for each simulation. Dots show data points more than 1.5 times the interquartile range above Q3 or below Q1. The mismatch between the initial mean ensemble bed and the reference bed is provided for comparison (the rightmost box).
Table 2. Simulation results
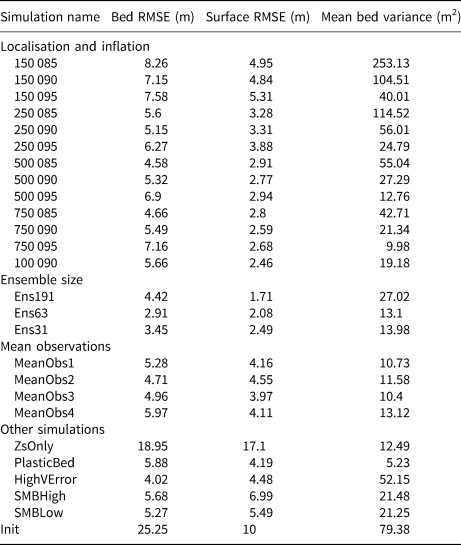
The bed RMSE is the root-mean-square error between the mean ensemble bed and the reference bed after the final analysis step. Surface RMSE is the root-mean-square error between the mean ensemble surface and the reference surface at the end of the simulation. The mean bed variance is calculated by taking the mean of the variance of the z coordinate at each bed node across the entire ensemble at the end of each simulation. The initial bed RMSE is 25.25 m (66.70 m for PlasticBed; 23.19 m for 3DTest) – the reference surface error is that found at the end of the no assimilation run: 14.65 m. Errors and STDs are reported solely for the glaciated portion of the model domain (x > 2400 m).
3.1. Localisation and inflation
We initially ran twelve simulations testing all combinations of localisation radii of 150, 250, 500 and 750 m, and inflation parameters of 0.85, 0.9 and 0.95. We found that, regardless of localisation, an inflation parameter of 0.9 produced a low bed RMSE, as well as the lowest volume error for localisation radii ⩾500 m (Fig. 3). We also ran an additional simulation (run 1 000 090) with a higher localisation parameter (1000 m) and an inflation of 0.9 to see if errors began to increase, given this localisation represented 20% of the model domain. A localisation radius of 750 m (run 750 090) produced almost exactly the same result as one of 500 m (run 500 090) or 250 m (run 250 090), with a bed RMSE of 5.49 m (compared to 5.32 and 5.15 m, respectively), though surface RMSE dropped from 3.31 m (run 250 090) to 2.59 m. Run 1 000 090 confirmed this trend, with bed RMSE increasing further to 5.66 m and surface RMSE dropping to 2.46 m. We therefore used a localisation radius of 750 m and an inflation parameter of 0.9 for all other simulations, as this provided what we judged to be the best combination of low bed and surface RMSE, combined with low volume error (a mismatch of only 0.5%, compared to 1.26% with a localisation radius of 250 m) that showed only negligible improvement with the higher 1000 m localisation radius. We note that simulations using an inflation of 0.95 produce lower mean variances (i.e. the ensemble spread is reduced), but these are examples of over-confident ensembles, as they are demonstrably worse at retrieving the actual bed position, measured by the RMSE metric.
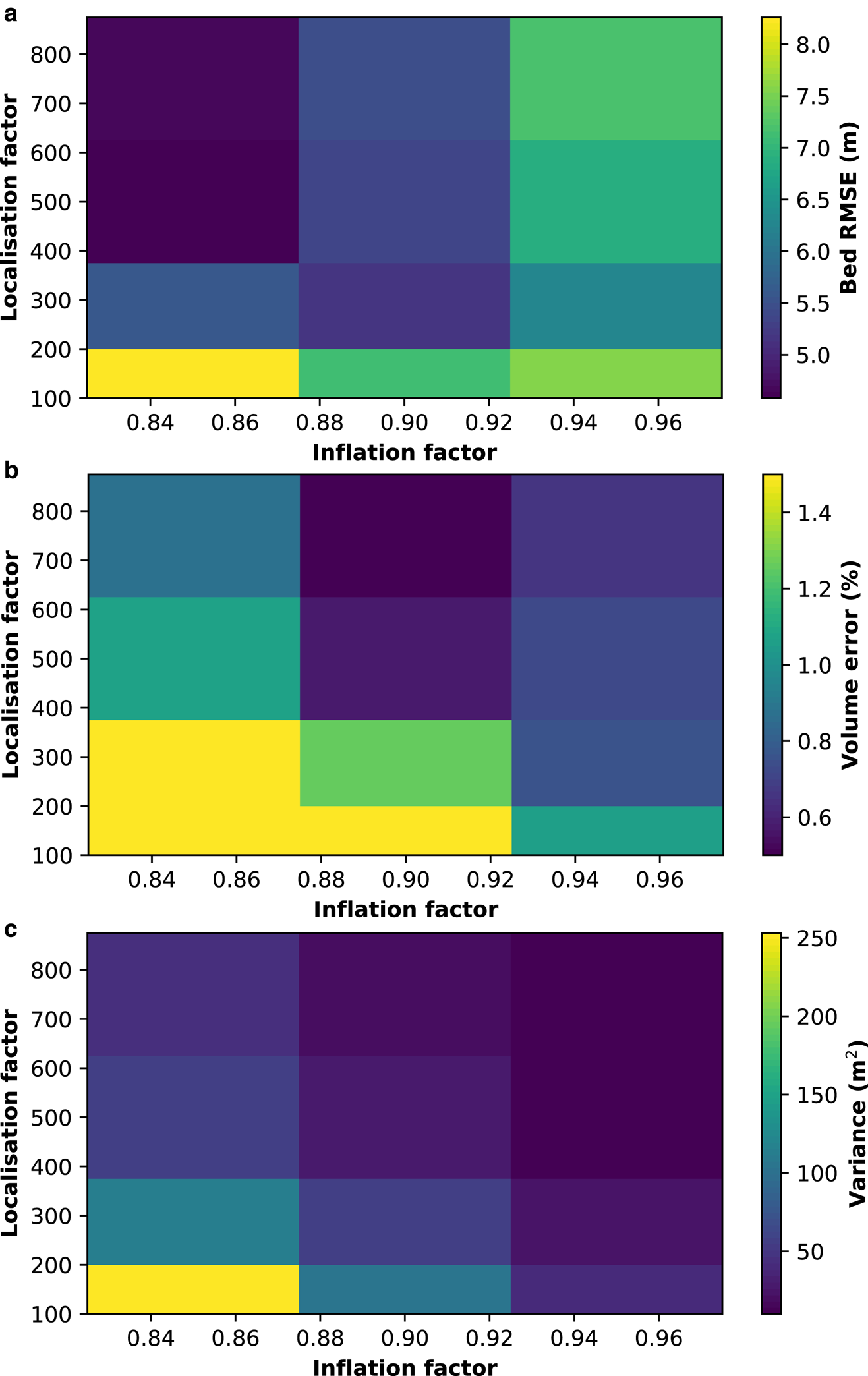
Figure 3. Heat map of root-mean-square error between the mean ensemble bed and the reference bed (panel a), error between the mean ensemble glacier volume and the reference glacier volume (panel b), and the mean bed variance for a range of localisation and inflation parameters. Note how an inflation value of 0.9 provides the best compromise between the three heat maps.
3.2. Ensemble size
To test the importance of the ensemble size, we replicated the 15-member ensemble 750 090 simulation with three larger ensembles of 191, 63 and 31 members (runs Ens191, Ens63 and Ens31). All three show an improvement on the bed RMSE vs 750 090, with results of 4.42, 2.91 and 3.45 m respectively, compared to 5.45 m. Investigating the performance of the ensembles further, it is also instructive to plot the rank histograms (Hamill, Reference Hamill2001) of observed velocities compared to modelled ensemble velocities at t = 25 (Fig. 3) to study whether the ensemble is biased and/or whether it is adequately sampling the range of values represented by the observations. A perfect ensemble should present a flat histogram with no substantial peaks or bias, as every observation should have an equal chance of filling every rank. Both the 191-member (Fig. 4a) and 63-member ensemble (Fig. 4b) come close to this ideal, with the most prominent ranks only exceeding the next lowest by 1 and no substantial clustering or bias. Looking at the 31-member ensemble (Fig. 4c), however, shows one peak at the extreme right-hand end of the distribution nearly 50% higher than the next highest peak, which suggests that the ensemble was not sufficiently sampling higher velocity values. A similar result is seen for the 15-member ensemble (Fig. 4d). Performing a chi-squared test to test whether all these distributions are significantly different from a uniform distribution, however, only returns a significant result at the P = 0.05 confidence interval for the 15-member ensemble, indicating the three larger ensembles are sufficiently sampling the range of observational values.

Figure 4. Rank histograms comparing modelled and observed velocity at t = 25 for a range of ensemble sizes. a 191 members (run Ens191); b 63 members (Ens63); c 31 members (Ens31); and d 15 members (750 090). Note different y-axis scales. There were 153 observations to be ranked and observational error was taken into account.
3.3. Mean observations
To investigate the (likely) case where only one set of observations, possibly averaged over several years, are available for a glacier, we ran four simulations (MeanObs1–4). There is little discernible pattern in the results: MeanObs1 (one year of observations, run to steady-state) has the lowest volume error of the four simulations (1.58%; not shown), while MeanObs2 (one year of observations, runs cut off after 10 years) has the lowest bed RMSE (4.71 m), and MeanObs3 (five years' averaged observations, run to steady-state) has the lowest surface RMSE (3.97 m). There is therefore no obvious conclusion as to which experimental protocol is the most effective.
3.4. Other simulations
Results from the ZsOnly run show that not including any velocity observations in the assimilation process led to a significant degradation in performance, with bed RMSE 3.45 times higher than for the 750 090 run, and surface RMSE increasing more than sixfold. The HighVError run, however, where the error on the velocity observations was increased to the same level as the maximum velocity magnitude, shows no significant decline in performance compared to 750 090: bed RMSE was lower, but surface RMSE and the volume error was higher. The SMBHigh and SMBLow simulations also show similar performance to the 750 090 simulation in terms of retrieving the reference bed, though the surface RMSE is more than double in both cases. The PlasticBed simulation (Fig. 5), where the initial ensemble beds were derived using a simple parameterisation based on glacier length and altitudinal range, further shows good performance. The bed RMSE is only slightly higher than for the 750 090 run, though the surface RMSE increases by a factor of 1.6, but, considering the lack of information provided to the model on the actual bed location, this is not surprising. The very low mean variance for this run (5.23) does however suggest that this ensemble is over-confident in its prediction, and could perform better with a reduced inflation parameter (i.e. more inflation).
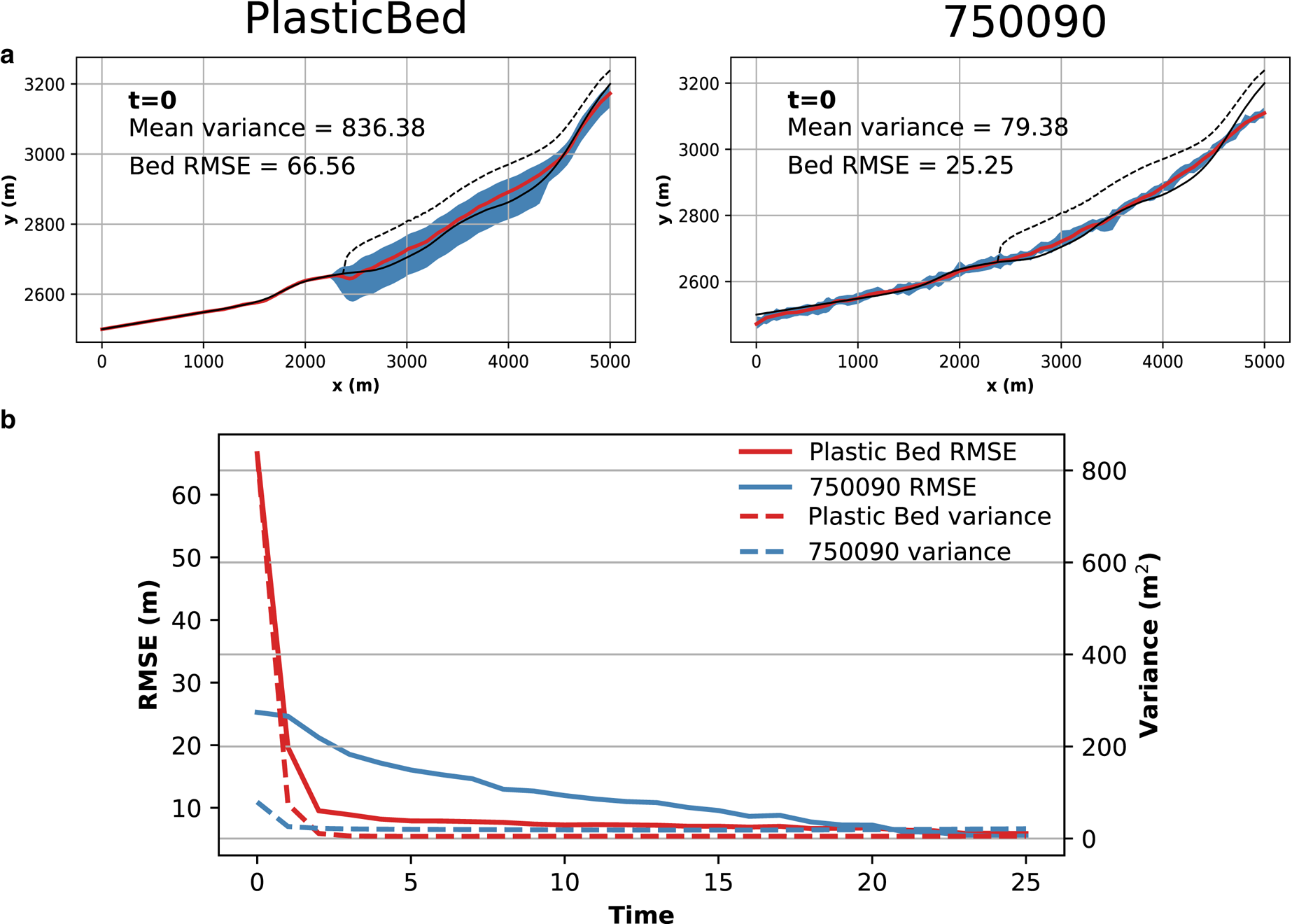
Figure 5. a. Comparison of initial mean ensemble bed (red line) and reference bed (black line) for PlasticBed simulation (left column) with 750 090 simulation provided as a reference (right column). The blue area represents the range of the ensemble and the dashed black line shows the mean ensemble surface. b. The evolution of bed RMSE (solid lines) and mean bed variance (dashed lines) for the PlasticBed (red lines) and 750 090 (blue lines) simulations. Note how the majority of the change takes places in the first three analysis steps for PlasticBed unlike for 750 090. For the purposes of the plastic flow assumption, the bed in the deglaciated area (the first 2300 m of the domain) was prescribed.
4. Discussion
Our findings clearly show the robustness of data assimilation using the ESTKF in successfully reconstructing a glacier bed across a wide range of scenarios. The worst-performing simulation (ZsOnly), after 100 years of model time, still manages to reduce the RMSE on the bed by over 20% compared to the no-assimilation simulation, while the best-performing simulations manage to reduce the surface RMSE by over sevenfold and the bed RMSE eightfold. The volume discrepancy between the reference and modelled glacier is also reduced from 5% to 1–2% for the majority of the assimilation scenarios, though the less-effective runs (150 085, 250 085, HighVError, ZsOnly, SMBHigh and SMBLow) report mismatches of 3–10%. This suggests our approach may be broadly applicable across real-world glaciers to retrieve unknown variables and/or to provide self-consistent initial states for prognostic simulations.
More specifically, several practical pointers for using the ESTKF and data assimilation on mountain glaciers can be drawn out from our findings. The first is that a value of 0.9–0.95 should be preferred for inflation – a value of 0.9 produces the lowest RMSEs here, while a value of 0.95 produces the lowest mean variance and volume mismatch, though this may be a sign of over-confidence in the ensemble, hence our preference for the lower value of 0.9. This agrees well with the preferred inflation factor of 0.92 used by Gillet-Chaulet (Reference Gillet-Chaulet2020). This inflation should be combined with a relatively high localisation radius – we only see substantially higher bed RMSEs once the localisation radius reaches 1000 m, or 20% of the total model domain. There is less evidence here for a negative relationship between localisation and inflation – as the localisation radius increases, both the lower-inflation (150 085, 250 085, 500 085, 750 085) and higher-inflation (150 095, 250 095, 500 095, 750 095) simulations perform better (with the exception of bed RMSEs for the higher-inflation simulations), though it is notable that both 500 085 and 750 085 return low bed RMSE values. This negative relationship would be expected, as increasing the localisation radius results in the assimilation of more observations, reducing the ensemble spread, which is then countered by increasing the inflation (Gillet-Chaulet, Reference Gillet-Chaulet2020), but it may be that the relatively small size of the domain and the small number of observations are obfuscating trends that would be more apparent on a larger glacier. Or that our relatively small ensemble size for a relatively small glacier leads to inflation having a more important role. Overall, though, our findings suggest a higher localisation radius is better than a lower one when considering mountain glaciers.
A further consideration here is the optimal ensemble size. Too small an ensemble risks undersampling the error subspace and reducing the performance of the assimilation; too large an ensemble will result in unnecessary computational costs (based on our setup in this study, each additional ensemble member represented roughly 32 h of extra core time). Based solely on the RMSEs between the ensemble mean and the reference state, an ensemble of as few as 15 members appears to be effective in a 2D case. However, studying the rank histograms and chi-squared testsfor each ensemble (Fig. 4), the 15-member ensemble is clearly undersampling the error subspace; its good performance here is therefore perhaps not to be generally relied on. The 31-member ensemble appears to have a substantial peak at one end of the distribution, but returns a P-value of 0.3, so is not too divergent from uniformity and perhaps represents a lower bound for reasonable ensemble sizes. The 63-member ensemble seems functionally indistinguishable from the 191-member ensemble, however, so we suggest that a minimum ensemble size of about 30 members and a maximum of 100 would be effective for 2D flowline simulations of mountain glaciers. This concords well with the findings of Gillet-Chaulet (Reference Gillet-Chaulet2020) for 2D flowline simulations of ice sheets, which indicates the optimal ensemble size may be more tied to the complexity of the simulation than the size of the model domain. More broadly, this also indicates that RMSEs and rank histograms may be more reliable indicators of ensemble performance than mean variance or volume mismatches (not that, in a real case, the volume will be known, making this metric inappropriate). Low mean variance can simply be the result of over-confidence and is not necessarily an indicator that the ensemble has correctly reconstructed the glacier bed, while a low volume mismatch may simply reflect this low ensemble spread, rather than a better reproduction of the reference glacier. It is also, of course, theoretically possible to have an excellent volume agreement with a very poorly reconstructed glacier, provided the relative position of the bed and surface happen to fall correctly.
We also show that repeatedly assimilating one set of observations averaged over a period of five years performs broadly as well as repeatedly assimilating one set of observations for a specific year and that, in both cases, the bed is still retrieved well, which points towards the method employed here being effective even on data-deficient glaciers. Perhaps more importantly, our results further show that, in this situation, running the forward model to a steady state after every analysis step produces no improvement in assimilation performance compared to running for a much shorter period. This agrees well with the method employed by Brinckerhoff-v2 in the ITMIX experiments (Farinotti and others, Reference Farinotti2017; Reference Farinotti2021), as well as work on Aru glacier by Gilbert and others (Reference Gilbert2018). Adopting this latter method results in more forward-model and analysis steps being needed until bed RMSE ceases decreasing (13 and 10 steps for MeanObs2 and MeanObs4, respectively, compared to 9 and 10 for MeanObs1 and MeanObs3), but the total model runtime is still far shorter (100–150 years compared to 450–500 years), making this approach more computationally attractive. We suggest that, on small mountain glaciers, the rapid response to changes in boundary conditions (such as the altered bed after every analysis step), means that the vast majority of model evolution as a consequence of the imposed change happens in the first few years of the simulation, so that simulating the extra years to reach a steady state brings little extra benefit in this case. The next dataset can, instead, be safely assimilated after only a few years of model running.
One very important outcome evident from our results is that incorporating even low-quality additional data into the assimilation process greatly improves its performance. Our ZsOnly run, where no surface velocities were provided, performed worst of all the simulations, with RMSEs on the bed and surface 3.5 and 6.6 times higher, respectively, than the 750 090 run to which it was otherwise identical. Our HighVError run, however, which used surface velocity observations with quintupled errors such that the error was equal to or exceeded the actual velocity signal, actually outperformed the 750 090 run on bed RMSE (though with considerably higher – more than double – ensemble spread and therefore uncertainty as measured by the variance), though was noticeably worse at reconstructing the surface (RMSE 1.7 times higher) and glacier volume (mismatch 9.4 times higher). Comparing HighVError and ZsOnly directly, HighVError has bed RMSE and surface RMSE, respectively, 4.7 and 3.8 times lower, as well as volume mismatch four times lower. It would therefore seem clear that assimilating even patchy, poor-quality or intermittent datasets is likely to lead to far better outcomes than leaving this data out would produce.
This point is further supported by the performance of the SMBLow and SMBHigh simulations, which deliberately imposed a 10% modification in the modelled SMB gradient to mimic the effect of poorly known SMB. While this, unsurprisingly, affected the surface profile of the resulting model glacier, the ability of the assimilation to reconstruct the glacier bed was essentially unaffected and comparable to the otherwise-identical 750 090 simulation. Consequently, even data with known inaccuracies can still be used as part of a successful data assimilation. It is, however, worth pointing out that we only tested the effect of a systematic bias in the SMB gradient, rather than the more likely real case of uncorrelated measurement uncertainty. In a real example, this would clearly be of concern and may lead to some reduction in the accuracy of the assimilation process. Though, given the other model runs with inaccurate data discussed here (PlasticBed, HighVError), we feel this effect is likely to be small.
We also show that assimilation can be effective in reconstructing the glacier bed even when no a priori information on the location of the bed is available. The PlasticBed run (Fig. 5), where the initial ensemble bed was constructed solely using a parameterisation based on readily observable surface features (Haeberli and Hoelzle, Reference Haeberli and Hoelzle1995), still managed to retrieve the reference bed (Fig. 5b) and surface reasonably well. This is despite substantial initial uncertainty reflected in the ensemble range (Fig. 5a). It is also worth noting that the PlasticBed simulation showed very little further evolution after the third analysis step (Fig. 5b), which again links in to our point about even patchy or intermittent datasets being useful inputs to the process – the model does not need 25 continuous years of good-quality observations in order to accomplish its task. PlasticBed does seem unusual in this, however – the other simulations all show greater change in later analysis steps. PlasticBed's rapid progress is most likely due to the much higher initial ensemble variance compared to the other 2D simulations (836.38 compared to 79.38), which pushes the analysis to trust the observations more than the initial ensemble and so collapses the ensemble towards the observations very quickly.
5. Conclusion
We run 25 2D Stokes flowline simulations using data assimilation in the Elmer/Ice modelling suite on a semi-synthetic glacier. We find that the assimilation method performs well in retrieving the reference glacier bed in a range of scenarios, with optimal inflation of 0.9 and localisation of 750 m. We show that, for this style of simulation, ensemble sizes of 50–100 members strike the best balance between performance and computational cost and that even assimilating only one set of observations repeatedly can still lead to successful bed reconstruction. We also demonstrate that the performance of the assimilation is greatly enhanced by the inclusion of surface velocity observations, even in cases where the signal-to-noise ratio ≈1, and that assimilation can be effective, even when provided with deliberately erroneous information. We additionally show that data assimilation functions well in finding the reference bed in situations where no a priori information on the bed is provided when constructing the initial ensemble beds.
Going forwards, we hope to extend this data-assimilation method to the 3D case and apply it to a realistic example, which will additionally require consideration of rheological uncertainties and appropriate sliding laws. We aim to test the method first on the Synthetic1 example provided as part of the ITMIX experiments, before applying it to the realistic case of the Mer de Glace. We are confident that the method is effective in a glaciological context and will be of great use for glacier modelling in the future.
Acknowledgements
This work was supported by the ANR-MAGIC project, grant ANR-19-CE01-0023 of the French Agence Nationale de la Recherche. SC also acknowledges UNIL for giving him time to work on the final version of the manuscript. JF has received funding from the European Union's Horizon 2020 research and innovation programme via the European Research Council (ERC) as a Starting Grant (StG) under grant agreement No 948290. All the computations presented in this paper were performed using the GRICAD infrastructure (https://gricad.univ-grenoble-alpes.fr), which is supported by Grenoble research communities.
Data availability
All data are available on request from the corresponding author or in the SwissUBase repository at https://doi.org/10.48657/5e4p-jr63.









