Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-56f9d74cfd-rpbls Total loading time: 0.251 Render date: 2022-06-25T12:04:22.282Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true }
  • English
The Journal of Symbolic Logic The Journal of Symbolic Logic

Article contents

More on regular reduced products

Published online by Cambridge University Press:  12 March 2014

Juliette Cara Kennedy  and
Saharon Shelah
Juliette Cara Kennedy
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68 (Gustaf Hällströmin Katu 2B), FI-00014, University of Helsinki, Finland, E-mail: juliette.kennedy@helsinki.fi
Saharon Shelah
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel, E-mail: shelah@math.huji.ac.il
Get access Rights & Permissions[Opens in a new window]

Abstract.

The authors show, by means of a finitary version 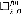of the combinatorial principle 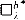of [7]. the consistency of the failure, relative to the consistency of supercompact cardinals, of the following: for all regular filters D on a cardinal λ. if Mi and Ni are elementarily equivalent models of a language of size ≤ λ, then the second player has a winning strategy in the Ehrenfeucht-Fraïssé game of length λ+ on ΠiMi/D and ΠiNi/D. If in addition 2λ = λ+ and i < λ implies |Mi| + |Ni| ≤ λ+ this means that the ultrapowers are isomorphic. This settles negatively conjecture 18 in [2].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 4 , December 2004 , pp. 1261 - 1266
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ben-David, S., On Shelah's compactness of cardinals, Israel Journal of Mathematics, vol. 31 (1978), pp. 34–56.CrossRefGoogle Scholar
[2]Chang, C. C. and Keisler, J., Model theory, North-Holland, 1990.Google Scholar
[3]Keisler, J., Ultraproducts and saturated models, Koninklijke Nederlandse Akademie van Wetenschappen, Proceedings Series A, vol. 67 (1964), pp. 178–186, (= Indagationes Mathematicae. New Series, vol. 26).Google Scholar
[4]Kennedy, J. and Shelah, S., On regular reduced products, this Journal, vol. 67 (2002), pp. 1169–1177.Google Scholar
[5]Kennedy, J. and Shelah, S., On embedding models of arithmetic of cardinality ℵ1 into reduced powers, Fundamenta Mathematicae, vol. 176 (2003), no. 1, pp. 17–24.CrossRefGoogle Scholar
[6]Shelah, S., Every two elementarily equivalent models have isomorphic ultrapowers, Israel Journal of Mathematics, vol. 10 (1971), pp. 224–233.CrossRefGoogle Scholar
[7]Shelah, S., “Gap 1” two-cardinal principles and the omitting types theorem for L(Q), Israel Journal of Mathematics, vol. 65 (1989), no. 2, pp. 133–152.CrossRefGoogle Scholar
2
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

More on regular reduced products
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

More on regular reduced products
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

More on regular reduced products
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *