In this paper we investigate omitting types for a certain kind of stable theories which we call stable ccc theories. In Theorem 2.1 we improve Steinhorn's result from [St]. We prove also some independence results concerning omitting types. The main results presented in this paper were part of the author's Ph.D. thesis [N1].

Throughout, we use the standard set-theoretic and model-theoretic notation, such as can be found for example in [Sh] or [M]. So in particular T is always a countable complete theory in the language L. We consider all models of T and all sets of parameters subsets of the monster model ℭ, which is very saturated. Ln(A) denotes the Lindenbaum-Tarski algebra of formulas with parameters from A and n free variables. We omit n in Ln(A) when n = 1 or when it is clear from the context what n is. If φ, ψ ∈ L(A) are consistent then we say that φ is below ψ if ψ⊢ψ. For a type p and a set A ⊆ ℭ, p(A) is the set of tuples of elements of A which satisfy p. Formulas are special cases of types. We say that a type p is isolated over A if, for some φ(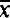) ∈ L(A), φ(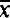) ⊢ p(x), i.e. φ isolates p. For a formula φ, [φ] denotes the class of types which contain φ. We assume that the reader is familiar with some basic knowledge of forking, as presented in [Sh, III] or [M].

Throughout, we work in ZFC. 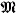and denote (countable) transitive models of ZFC. cov K is the minimal number of meager sets covering the real line R. In this paper we prove theorems showing connections between omitting types and the combinatorics of the real line. More results in this direction are presented in [N2] and [N3].