Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T06:30:29.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramsey-like cardinals II

Published online by Cambridge University Press:  12 March 2014

Victoria Gitman  and
P. D. Welch
Victoria Gitman
Affiliation:
New York City College of Technology (CUNY), 300 Jay Street, Brooklyn, NY 11201, USA, E-mail: vgitman@nylogic.org
P. D. Welch
Affiliation:
University of Bristol, School of Mathematics, University of Bristol Clifton, Bristol, BS8 1TW, UK, E-mail: P.Welch@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper continues the study of the Ramsey-like large cardinals introduced in [5] and [14]. Ramsey-like cardinals are defined by generalizing the characterization of Ramsey cardinals via the existence of elementary embeddings. Ultrafilters derived from such embeddings are fully iterable and so it is natural to ask about large cardinal notions asserting the existence of ultrafilters allowing only α-many iterations for some countable ordinal α. Here we study such α-iterable cardinals. We show that the α-iterable cardinals form a strict hierarchy for α ≤ ω1, that they are downward absolute to L for 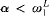, and that the consistency strength of Schindler's remarkable cardinals is strictly between 1-iterable and 2-iterable cardinals.

We show that the strongly Ramsey and super Ramsey cardinals from [5] are downward absolute to the core model K. Finally, we use a forcing argument from a strongly Ramsey cardinal to separate the notions of Ramsey and virtually Ramsey cardinals. These were introduced in [14] as an upper bound on the consistency strength of the Intermediate Chang's Conjecture.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 541 - 560
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beller, A., Jensen, R., and Welch, P., Coding the universe, London Mathematical Society Lecture Note Series, vol. 47, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[2]Donder, Hans-Dieter and Levinski, Jean-Pierre, Some principles related to Chang's conjecture, Annals of Pure and Applied Logic, vol. 45 (1989), no. 1, pp. 39–101.CrossRefGoogle Scholar
[3]Feng, Q., A hierarchy of Ramsey cardinals, Annals of Pure and Applied Logic, vol. 49 (1990), no. 3, pp. 257–277.CrossRefGoogle Scholar
[4]Gaifman, H., Elementary embeddings of models of set-theory and certain subtheories, Axiomatic set theory (Proceedings of the Symposium on Pure Mathematics, vol. XIII, part II, University of California, Los Angeles, California, 1967), American Mathematical Society, Providence, R.I., 1974, pp. 33–101.Google Scholar
[5]Gitman, V., Ramsey-like cardinals, this Journal, vol. 76 (2011), no. 2, pp. 519–540.Google Scholar
[6]Gitman, V. and Johnstone, T., Indestructibility for Ramsey-like cardinals, in preparation, 2010.Google Scholar
[7]Hamkins, J. D., Forcing and large cardinals, manuscript, 2007.Google Scholar
[8]Kanamori, A., The higher infinite, second ed., Springer Monographs in Mathematics, Springer–Verlag, New York, 2003.Google Scholar
[9]Kunen, K., Some applications of iterated ultrapowers in set theory, Annals of Pure and Applied Logic, vol. 1 (1970), pp. 179–227.Google Scholar
[10]Kunen, K., Saturated ideals, this Journal, vol. 43 (1978), no. 1, pp. 65–76.Google Scholar
[11]Mitchell, W. J., Ramsey cardinals and constructibility, this Journal, vol. 44 (1979), no. 2, pp. 260–266.Google Scholar
[12]Schindler, R., Semi-proper forcing, remarkable cardinals, and Bounded Martin's Maximum, Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 527–532.CrossRefGoogle Scholar
[13]Villaveces, A., Chains of end elementary extensions of models of set theory, this Journal, vol. 63 (1998), no. 3, pp. 1116–1136.Google Scholar
[14]Welch, P. D. and Sharpe, I., Greatly Erdős cardinals and some generalizations to the Chang and Ramsey properties, Annals of Pure and Applied Logic, to appear.Google Scholar
[15]Zeman, M., Inner models and large cardinals, de Gruyter Series in Logic and its Applications, vol. 5, Walter de Gruyter & Co., Berlin, 2002.CrossRefGoogle Scholar