Article contents
FURTHER RESULTS ON VANISHING COEFFICIENTS IN INFINITE PRODUCT EXPANSIONS
Published online by Cambridge University Press: 11 November 2014
Abstract
We extend results of Andrews and Bressoud [‘Vanishing coefficients in infinite product expansions’, J. Aust. Math. Soc. Ser. A27(2) (1979), 199–202] on the vanishing of coefficients in the series expansions of certain infinite products. These results have the form that if 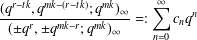 $$\begin{eqnarray}\frac{(q^{r-tk},q^{mk-(r-tk)};q^{mk})_{\infty }}{(\pm q^{r},\pm q^{mk-r};q^{mk})_{\infty }}=:\mathop{\sum }_{n=0}^{\infty }c_{n}q^{n}\end{eqnarray}$$
$$\begin{eqnarray}\frac{(q^{r-tk},q^{mk-(r-tk)};q^{mk})_{\infty }}{(\pm q^{r},\pm q^{mk-r};q^{mk})_{\infty }}=:\mathop{\sum }_{n=0}^{\infty }c_{n}q^{n}\end{eqnarray}$$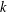 $k$,
$k$, 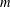 $m$,
$m$,  $s$ and
$s$ and  $t$, where
$t$, where 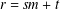 $r=sm+t$, then
$r=sm+t$, then 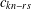 $c_{kn-rs}$ is always zero. Our theorems also partly give a simpler reformulation of results of Alladi and Gordon [‘Vanishing coefficients in the expansion of products of Rogers–Ramanujan type’, in: The Rademacher Legacy to Mathematics (University Park, PA, 1992), Contemporary Mathematics, 166 (American Mathematical Society, Providence, RI, 1994), 129–139], but also give results for cases not covered by the theorems of Alladi and Gordon. We also give some interpretations of the analytic results in terms of integer partitions.
$c_{kn-rs}$ is always zero. Our theorems also partly give a simpler reformulation of results of Alladi and Gordon [‘Vanishing coefficients in the expansion of products of Rogers–Ramanujan type’, in: The Rademacher Legacy to Mathematics (University Park, PA, 1992), Contemporary Mathematics, 166 (American Mathematical Society, Providence, RI, 1994), 129–139], but also give results for cases not covered by the theorems of Alladi and Gordon. We also give some interpretations of the analytic results in terms of integer partitions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 14
- Cited by




