Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T20:17:22.507Z Has data issue: false hasContentIssue false
  • English
  • Français

$L^{q}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS IN THE ABSENCE OF SECOND-ORDER IDENTITIES

Part of: Classical measure theory

Published online by Cambridge University Press:  22 August 2018

SZE-MAN NGAI  and
YUANYUAN XIE
SZE-MAN NGAI*
Affiliation:
College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China Department of Mathematical Sciences, Georgia Southern University, Statesboro, GA 30460-8093, USA email smngai@georgiasouthern.edu
YUANYUAN XIE
Affiliation:
Key Laboratory of High Performance Computing and Stochastic Information Processing (HPCSIP), (Ministry of Education of China), College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, PR China email xieyuanyuan198767@163.com
*
✉smngai@georgiasouthern.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the class of self-similar measures in 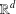$\mathbb{R}^{d}$ with overlaps that are essentially of finite type, we set up a framework for deriving a closed formula for the 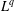$L^{q}$-spectrum of the measure for 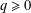$q\geq 0$. This framework allows us to include iterated function systems that have different contraction ratios and those in higher dimension. For self-similar measures with overlaps, closed formulas for the $L^{q}$-spectrum have only been obtained earlier for measures satisfying Strichartz’s second-order identities. We illustrate how to use our results to prove the differentiability of the 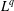$L^{q}$-spectrum, obtain the multifractal dimension spectrum, and compute the Hausdorff dimension of the measure.

Keywords

fractalLq-spectrummultifractal formalismself-similar measureessentially of finite type

MSC classification

Primary: 28A80: Fractals 28A78: Hausdorff and packing measures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 1 , February 2019 , pp. 56 - 103
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are supported in part by the National Natural Science Foundation of China, grants 11771136 and 11271122, and Construct Program of the Key Discipline in Hunan Province. The first author is also supported by the Center of Mathematical Sciences and Applications (CMSA) of Harvard University, the Hunan Province Hundred Talents Program, and a Faculty Research Scholarly Pursuit Award from Georgia Southern University.

References

Cawley, R. and Mauldin, R. D., ‘Multifractal decompositions of Moran fractals’, Adv. Math. 92 (1992), 196–236.Google Scholar
Deng, G. and Ngai, S.-M., ‘Differentiability of L q -spectrum and multifractal decomposition by using infinite graph-directed IFSs’, Adv. Math. 311 (2017), 190–237.Google Scholar
Edgar, G. A. and Mauldin, R. D., ‘Multifractal decompositions of digraph recursive fractals’, Proc. Lond. Math. Soc. (3) 65 (1992), 604–628.Google Scholar
Feng, D.-J., ‘The limited Rademacher functions and Bernoulli convolutions associated with Pisot numbers’, Adv. Math. 195 (2005), 24–101.Google Scholar
Feng, D. J. and Lau, K.-S., ‘Multifractal formalism for self-similar measures with weak separation condition’, J. Math. Pures Appl. (9) 92 (2009), 407–428.Google Scholar
Feng, D.-J. and Olivier, E., ‘Multifractal analysis of weak Gibbs measures and phase transition–application to some Bernoulli convolutions’, Ergodic Theory Dynam. Systems 23 (2003), 1751–1784.Google Scholar
Frisch, U. and Parisi, G., ‘On the singularity structure of fully developed turbulence’, in: Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics (eds. Ghil, M., Benzi, R. and Parisi, G.) (North-Holland, Amsterdam–New York, 1985), 84–88.Google Scholar
Halsey, T. C., Jensen, M. H., Kadanoff, L. P., Procaccia, I. and Shraiman, B. I., ‘Fractal measures and their singularities: the characterization of strange sets’, Phys. Rev. A 33 (1986), 1141–1151.Google Scholar
Heurteaux, Y., ‘Estimations de la dimension inférieure et de la dimension supérieure des mesures’, Ann. Inst. Henri Poincaré Probab. Stat. 34 (1998), 309–338; (in French).Google Scholar
Jin, N. and Yau, S. S. T., ‘General finite type IFS and M-matrix’, Comm. Anal. Geom. 13 (2005), 821–843.Google Scholar
Lau, K.-S., ‘Fractal measures and mean p-variations’, J. Funct. Anal. 108 (1992), 427–457.Google Scholar
Lau, K.-S. and Ngai, S.-M., ‘ L q -spectrum of the Bernoulli convolution associated with the golden ratio’, Studia Math. 131 (1998), 225–251.Google Scholar
Lau, K.-S. and Ngai, S.-M., ‘Multifractal measures and a weak separation condition’, Adv Math. 141 (1999), 45–96.Google Scholar
Lau, K.-S. and Ngai, S.-M., ‘Second-order self-similar identities and multifractal decompositions’, Indiana Univ. Math. J. 49 (2000), 925–972.Google Scholar
Lau, K.-S. and Ngai, S.-M., ‘A generalized finite type condition for iterated function systems’, Adv. Math. (2007), 647–671.Google Scholar
Lau, K.-S., Wang, J. and Chu, C.-H., ‘Vector-valued Choquet-Deny theorem, renewal equation and self-similar measures’, Studia Math. 117 (1995), 1–28.Google Scholar
Lau, K.-S. and Wang, X.-Y., ‘Iterated function systems with a weak separation condition’, Studia Math. 161 (2004), 249–268.Google Scholar
Lau, K.-S. and Wang, X. Y., ‘Some exceptional phenomena in multifractal formalism: part I’, Asian J. Math. 9 (2005), 275–294.Google Scholar
Ngai, S.-M., ‘A dimension result arising from the L q -spectrum of a measure’, Proc. Amer. Math. Soc. 125 (1997), 2943–2951.Google Scholar
Ngai, S.-M., ‘Spectral asymptotics of Laplacians associated with one-dimensional iterated function systems with overlaps’, Canad. J. Math. 63 (2011), 648–688.Google Scholar
Ngai, S.-M., Tang, W. and Xie, Y., ‘Spectral asymptotics of one-dimensional fractal Laplacians in the absence of second-order identities’, Discrete Contin. Dyn. Syst. 38 (2018), 1849–1887.Google Scholar
Ngai, S.-M. and Wang, Y., ‘Hausdorff dimension of self-similar sets with overlaps’, J. Lond. Math. Soc. (2) 63 (2001), 655–672.Google Scholar
Olsen, L., ‘A multifractal formalism’, Adv. Math. 116 (1995), 82–196.Google Scholar
Strichartz, R. S., ‘Self-similar measures and their Fourier transforms III’, Indiana Univ. Math. J. 42 (1993), 367–411.Google Scholar