Article contents
ON A NEW CIRCLE PROBLEM
Published online by Cambridge University Press: 08 November 2016
Abstract
We attempt to discuss a new circle problem. Let 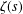 $\unicode[STIX]{x1D701}(s)$ denote the Riemann zeta-function
$\unicode[STIX]{x1D701}(s)$ denote the Riemann zeta-function 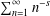 $\sum _{n=1}^{\infty }n^{-s}$ (
$\sum _{n=1}^{\infty }n^{-s}$ ( 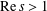 $\text{Re}\,s>1$ ) and
$\text{Re}\,s>1$ ) and 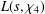 $L(s,\unicode[STIX]{x1D712}_{4})$ the Dirichlet
$L(s,\unicode[STIX]{x1D712}_{4})$ the Dirichlet 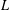 $L$ -function
$L$ -function 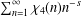 $\sum _{n=1}^{\infty }\unicode[STIX]{x1D712}_{4}(n)n^{-s}$ (
$\sum _{n=1}^{\infty }\unicode[STIX]{x1D712}_{4}(n)n^{-s}$ ( 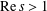 $\text{Re}\,s>1$ ) with the primitive Dirichlet character mod 4. We shall define an arithmetical function
$\text{Re}\,s>1$ ) with the primitive Dirichlet character mod 4. We shall define an arithmetical function 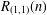 $R_{(1,1)}(n)$ by the coefficient of the Dirichlet series
$R_{(1,1)}(n)$ by the coefficient of the Dirichlet series 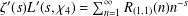 $\unicode[STIX]{x1D701}^{\prime }(s)L^{\prime }(s,\unicode[STIX]{x1D712}_{4})=\sum _{n=1}^{\infty }R_{(1,1)}(n)n^{-s}$
$\unicode[STIX]{x1D701}^{\prime }(s)L^{\prime }(s,\unicode[STIX]{x1D712}_{4})=\sum _{n=1}^{\infty }R_{(1,1)}(n)n^{-s}$ 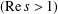 $(\text{Re}\,s>1)$ . This is an analogue of
$(\text{Re}\,s>1)$ . This is an analogue of 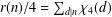 $r(n)/4=\sum _{d|n}\unicode[STIX]{x1D712}_{4}(d)$ . In the circle problem, there are many researches of estimations and related topics on the error term in the asymptotic formula for
$r(n)/4=\sum _{d|n}\unicode[STIX]{x1D712}_{4}(d)$ . In the circle problem, there are many researches of estimations and related topics on the error term in the asymptotic formula for 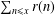 $\sum _{n\leq x}r(n)$ . As a new problem, we deduce a ‘truncated Voronoï formula’ for the error term in the asymptotic formula for
$\sum _{n\leq x}r(n)$ . As a new problem, we deduce a ‘truncated Voronoï formula’ for the error term in the asymptotic formula for 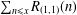 $\sum _{n\leq x}R_{(1,1)}(n)$ . As a direct application, we show the mean square for the error term in our new problem.
$\sum _{n\leq x}R_{(1,1)}(n)$ . As a direct application, we show the mean square for the error term in our new problem.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 231 - 249
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
This work is supported by JSPS KAKENHI: 26400030, 15K17512, and 15K04778.
References
- 2
- Cited by

