No CrossRef data available.
Article contents
REAL THETA CHARACTERISTICS AND AUTOMORPHISMS OF A REAL CURVE
Published online by Cambridge University Press: 22 January 2010
Abstract
Let X be a geometrically irreducible smooth projective curve defined over ℝ, of genus at least 2, that admits a nontrivial automorphism, σ. Assume that X does not have any real points. Let τ be the antiholomorphic involution of the complexification xℂ of X. We show that if the action of σ on the set 𝒮(X) of all real theta characteristics of X is trivial, then the order of σ is even, say 2k, and the automorphism 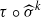 of Xℂ has a fixed point, where
of Xℂ has a fixed point, where 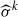 is the automorphism of X×ℝℂ defined by σ. We then show that there exists X with a real point and admitting a nontrivial automorphism σ, such that the action of σ on 𝒮(X) is trivial, while X/〈σ〉≠ℙ1ℝ. We also give an example of X with no real points and admitting a nontrivial automorphism σ, such that the automorphism
is the automorphism of X×ℝℂ defined by σ. We then show that there exists X with a real point and admitting a nontrivial automorphism σ, such that the action of σ on 𝒮(X) is trivial, while X/〈σ〉≠ℙ1ℝ. We also give an example of X with no real points and admitting a nontrivial automorphism σ, such that the automorphism 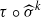 has a fixed point, the action of σ on 𝒮(X) is trivial, and X/〈σ〉≠ℙ1ℝ.
has a fixed point, the action of σ on 𝒮(X) is trivial, and X/〈σ〉≠ℙ1ℝ.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Publishing Association Inc. 2010

