2-convexity and 2-concavity in Schatten ideals
Published online by Cambridge University Press: 24 October 2008
Extract
The properties p-convexity and q-concavity are fundamental in the study of Banach sequence spaces (see [L-TzII]), and in recent years have been shown to be of great significance in the theory of the corresponding Schatten ideals ([G-TJ], [LP-P] and many other papers). In particular, the notions 2-convex and 2-concave are meaningful in Schatten ideals. It seems to have been noted only recently [LP-P] that a Schatten ideal has either of these properties if the underlying sequence space has. One way of establishing this is to use the fact that if (E, ‖ ‖E) is 2-convex, then there is another Banach sequence space (F, ‖ ‖F) such that ‖x;‖ 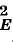 = ‖x2‖F for all x ε E. The 2-concave case can then be deduced using duality, though this raises some difficulties, for example when E is inseparable.
= ‖x2‖F for all x ε E. The 2-concave case can then be deduced using duality, though this raises some difficulties, for example when E is inseparable.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 4 , November 1996 , pp. 697 - 702
- Copyright
- Copyright © Cambridge Philosophical Society 1996
References
REFERENCES
- 1
- Cited by




