Article contents
Generalized Schwarzian derivatives and higher order differential equations
Published online by Cambridge University Press: 20 June 2011
Abstract
It is shown that the well-known connection between the second order linear differential equation h″ + B(z)h = 0, with a solution base {h1, h2}, and the Schwarzian derivative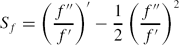 of f = h1/h2, can be extended to the equation h(k) + B(z) h = 0 where k ≥ 2. This generalization depends upon an appropriate definition of the generalized Schwarzian derivative Sk(f) of a function f which is induced by k−1 ratios of linearly independent solutions of h(k) + B(z) h = 0. The class
of f = h1/h2, can be extended to the equation h(k) + B(z) h = 0 where k ≥ 2. This generalization depends upon an appropriate definition of the generalized Schwarzian derivative Sk(f) of a function f which is induced by k−1 ratios of linearly independent solutions of h(k) + B(z) h = 0. The class  k(Ω) of meromorphic functions f such that Sk(f) is analytic in a given domain Ω is also completely described. It is shown that if Ω is the unit disc
k(Ω) of meromorphic functions f such that Sk(f) is analytic in a given domain Ω is also completely described. It is shown that if Ω is the unit disc  or the complex plane
or the complex plane  , then the order of growth of f ∈
, then the order of growth of f ∈ 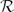 k(Ω) is precisely determined by the growth of Sk(f), and vice versa. Also the oscillation of solutions of h(k) + B(z) h = 0, with the analytic coefficient B in
k(Ω) is precisely determined by the growth of Sk(f), and vice versa. Also the oscillation of solutions of h(k) + B(z) h = 0, with the analytic coefficient B in 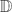 or
or  , in terms of the exponent of convergence of solutions is briefly discussed.
, in terms of the exponent of convergence of solutions is briefly discussed.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 151 , Issue 2 , September 2011 , pp. 339 - 354
- Copyright
- Copyright © Cambridge Philosophical Society 2011
References
REFERENCES
- 1
- Cited by

