Hostname: page-component-84b7d79bbc-g7rbq Total loading time: 0 Render date: 2024-07-25T21:37:55.775Z Has data issue: false hasContentIssue false
  • English
  • Français

On the arithmetic of a family of degree - two K3 surfaces

Published online by Cambridge University Press:  27 March 2018

FLORIAN BOUYER ,
EDGAR COSTA ,
DINO FESTI ,
CHRISTOPHER NICHOLLS  and
MCKENZIE WEST
FLORIAN BOUYER
Affiliation:
School of Mathematics, Howard House, Queen's Avenue, BS81SD, University of Bristol. e-mail: f.j.s.c.bouyer@gmail.com
EDGAR COSTA
Affiliation:
Department of Mathematics, Dartmouth College, 27 N. Main Street, 6188 Kemeny Hall, Hanover, NH 03755-3551, U.S.A. e-mail: edgarcosta@math.dartmouth.edu
DINO FESTI
Affiliation:
Institut für Mathematik, Johannes Gutenberg–Universität Mainz, Staudingerweg 9, 55128 Mainz, Germany. e-mail: dinofesti@gmail.com
CHRISTOPHER NICHOLLS
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG. e-mail: christopher.nicholls@balliol.ox.ac.uk
MCKENZIE WEST
Affiliation:
Department of Mathematics, 1200 Academy Street, Kalamazoo MI 49006, U.S.A.Kalamazoo College e-mail: mckenzie.west@kzoo.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ℙ denote the weighted projective space with weights (1, 1, 1, 3) over the rationals, with coordinates x, y, z and w; let 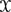$\mathcal{X}$ be the generic element of the family of surfaces in ℙ given by

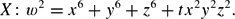\begin{equation*} X\colon w^2=x^6+y^6+z^6+tx^2y^2z^2. \end{equation*}
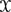The surface $\mathcal{X}$ is a K3 surface over the function field ℚ(t). In this paper, we explicitly compute the geometric Picard lattice of 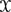$\mathcal{X}$, together with its Galois module structure, as well as derive more results on the arithmetic of 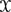$\mathcal{X}$ and other elements of the family X.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 3 , May 2019 , pp. 523 - 542
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BCFNW17] Bouyer, F., Costa, E., Festi, D., Nicholls, C. and West, M.. Accompanying MAGMA code. http://www.staff.uni-mainz.de/dfesti/AWS2015Magma.txt (2017).Google Scholar
[BCP97] Bosma, W., Cannon, J. and Playoust, C. The Magma algebra system. I. The user language. J. Symbolic Comput. 24 (3-4) (1997), 235–265. Computational algebra and number theory (London, 1993).10.1006/jsco.1996.0125Google Scholar
[BHPVdV04] Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A. Compact complex surfaces volume 4 of Ergeb. Math. Grenzgeb. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. (Springer-Verlag, Berlin, second edition, 2004).Google Scholar
[BT00] Bogomolov, F. A. and Tschinkel, Yu. Density of rational points on elliptic K3 surfaces. Asian J. Math. 4 (2) (2000), 351–368.10.4310/AJM.2000.v4.n2.a6Google Scholar
[Cha14] Charles, F. On the Picard number of K3 surfaces over number fields. Algebra Number Theory 8 (1) (2014), 1–17.10.2140/ant.2014.8.1Google Scholar
[CS99] Conway, J. H. and Sloane, N. J. A. Sphere packings, lattices and groups. Grundlehren Math Wiss vol. 290 [Fundamental Principles of Mathematical Sciences]. (Springer-Verlag, New York, third edition, 1999). With additional contributions by Bannai, E., Borcherds, R. E., Leech, J., Norton, S. P., Odlyzko, A. M., Parker, R. A., Queen, L. and Venkov, B. B.Google Scholar
[Dol96] Dolgachev, I. V. Mirror symmetry for lattice polarised K3 surfaces. J. Math. Sci. 81 (3) (1996), 2599–2630. Algebraic geometry, 4.10.1007/BF02362332Google Scholar
[EJ08] Elsenhans, A.-S. and Jahnel, J. K3 surfaces of Picard rank one and degree two. In Algorithmic number theory Lecture Notes in Comput. Sci. vol. 5011 (Springer, Berlin, 2008), pp. 212–225.10.1007/978-3-540-79456-1_14Google Scholar
[EJ11] Elsenhans, A.-S. and Jahnel, J. The Picard group of a K3 surface and its reduction modulo p. Algebra Number Theory 5 (8) (2011), 1027–1040.10.2140/ant.2011.5.1027Google Scholar
[Fes16] Festi, D. Topics in the arithmetic of del Pezzo and K3 surfaces. PhD. thesis. Universiteit Leiden (2016).Google Scholar
[Har77] Hartshorne, R. Algebraic geometry Graduate Texts in Math. No. 52. (Springer-Verlag, New York-Heidelberg, 1977).10.1007/978-1-4757-3849-0Google Scholar
[HKT13] Hassett, B., Kresch, A. and Tschinkel, Y. Effective computation of Picard groups and Brauer–Manin obstructions of degree two K3 surfaces over number fields. Rendiconti del Circolo Matematico di Palermo 62 (1) (2013), 137–151.10.1007/s12215-013-0116-8Google Scholar
[HS00] Hindry, M. and Silverman, J. H. Diophantine geometry: an introduction Graduate Texts in Math. vol. 201 (Springer-Verlag, New York, 2000).10.1007/978-1-4612-1210-2Google Scholar
[Huy16] Huybrechts, D. Lectures on K3 surfaces Camb. Stud. Adv. Math. vol. 158 (Cambridge University Press, Cambridge, 2016).10.1017/CBO9781316594193Google Scholar
[Ino78] Inose, H. Defining equations of singular K3 surfaces and a notion of isogeny. In Proceedings of the International Symposium on Algebraic Geometry (Kyoto Univ., Kyoto, 1977) (Kinokuniya Book Store, Tokyo, 1978), pp. 495–502.Google Scholar
[KT04] Kresch, A. and Tschinkel, Y. On the arithmetic of del Pezzo surfaces of degree 2. Proc. London Math. Soc. (3) 89 (3) (2004), 545–569.10.1112/S002461150401490XGoogle Scholar
[MP12] Maulik, D. and Poonen, B. Néron-Severi groups under specialisation. Duke Math. J. 161 (11) (2012), 2167–2206.10.1215/00127094-1699490Google Scholar
[Mum70] Mumford, D. Abelian varieties. Tata Institute of Fundamental Research Studies in Mathematics, No. 5. Published for the Tata Institute of Fundamental Research, Bombay (Oxford University Press, London, 1970).Google Scholar
[Nik80a] Nikulin, V. V. Integer symmetric bilinear forms and some of their geometric applications. Math USSR-Izv 14 (1) (1980), 103–167.10.1070/IM1980v014n01ABEH001060Google Scholar
[Nik80b] Nikulin, V. V. Integral symmetric bilinear forms and some of their applications. Mathematics of the USSR-Izvestiya, 14 (1) (1980), 103.10.1070/IM1980v014n01ABEH001060Google Scholar
[PTvL15] Poonen, B., Testa, D. and Luijk, R. van Computing Néron-Severi groups and cycle class groups. Compositio. Math. 151 (4) (2015), 713–734.10.1112/S0010437X14007878Google Scholar
[SS10] Schütt, M. and Shioda, T. Elliptic surfaces. In Algebraic geometry in East Asia–-Seoul 2008 Adv. Stud. Pure Math. vol. 60 (Math. Soc. Japan, Tokyo, 2010), pp. 51–160.Google Scholar
[ST10] Stoll, M. and Testa, D. The surface parametrising cuboids. arXiv:1009.0388 (2010).Google Scholar
[VAV11] Várilly–Alvarado, A. and Viray, B. Failure of the Hasse principle for Enriques surfaces. Adv. Math. 226 (6) (2011), 4884–4901.10.1016/j.aim.2010.12.020Google Scholar
[vL07] van Luijk, R. An elliptic K3 surface associated to Heron triangles. J. Number Theory 123 (1) (2007), 92–119.10.1016/j.jnt.2006.06.006Google Scholar