Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-20T01:33:20.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Brownian motion can see a knot

Published online by Cambridge University Press:  24 October 2008

N. Th. Varopoulos
N. Th. Varopoulos
Affiliation:
Université de Paris VI
Get access Rights & Permissions [Opens in a new window]

Extract

Let 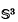be the 3-dimensional sphere and let 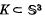be a smooth knot, i.e. K is the image of a regular diffeomorphism 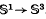. We say that K is unknotted if there exists a diffeomorphism of 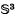onto the unit sphere of 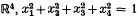, that brings K to the equatorial circle 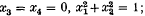otherwise we say that K is knotted.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 299 - 309
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carne, T. K.. Private communication.Google Scholar
[2]Deny, J.. Méthodes hilbertiennes en théorie du potentiel. In Potential Theory (C.I.M.E. 1969) (Edizioni Cremonese, 1970), 121–201.Google Scholar
[3]Gromov, M.. Groups of polynomial growth and expanding maps. Publ. Math. I.H.E.S. 53 (1981), 53–73.CrossRefGoogle Scholar
[4]Guivarc'h, Y., Keane, M. S. and Roynette, B.. Marches aléatoires sur les groupes de Lie. Lecture Notes in Mathematics, vol. 624 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[5]Itô, K. and McKean, H. P.. Diffusion Processes and their Sample Paths. Die Grundlehren der math. Wissenschaften Band 125 (Springer-Verlag, 1965).Google Scholar
[6]Milnor, J.. A note on curvature and fundamental group. J. Differential Geom. 2 (1968), 1–7.CrossRefGoogle Scholar
[7]Neuwirth, L. P.. Knot Groups. Ann. of Math. Studies, no. 56 (Princeton University Press, 1965).Google Scholar
[8]Stillwell, J.. Classical Topology and Combinatorial Group Theory. Graduate Texts in Math., vol. 72 (Springer-Verlag, 1980).CrossRefGoogle Scholar
[9]Varopoulos, N. Th.. Brownian motion and transient groups. Ann. Inst. Fourier 33 (1983), 241–261.CrossRefGoogle Scholar
[10]Varopoulos, N. Th.. Brownian motion and random walks on manifolds. Ann. Inst. Fourier 34 (1984), 243–269.CrossRefGoogle Scholar
[11]Varopoulos, N. Th.. Ark. Mat. (to appear).Google Scholar
[12]Varopoulos, N. Th.. Groupes transients en analyse complexe. C.R. Acad. Sci. Paris 297 (1983), Sér. I, 585–586.Google Scholar
[13]Varopoulos, N. Th.. Chaînes de Markov et inégalités isopérimétriques. C.R. Acad. Sci. Paris 298 (1984), Sér. I, 233–236.Google Scholar
[14]Varopoulos, N. Th.. Potential theory and diffusion on Riemannian manifolds. In Conference on Harmonic Analysis in Honor of Antoni Zygmund, vol. II (Wadsworth, 1983), 821–837.Google Scholar
[15]Williams, D.. Diffusions, Markov Processes and Martingales (J. Wiley, 1979).Google Scholar