Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-21T05:14:12.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugate Banach spaces

Published online by Cambridge University Press:  24 October 2008

A. F. Ruston
A. F. Ruston
Affiliation:
Department of Pure MathematicsUniversity of Sheffield
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this note is to present two characterizations of conjugate Banach spaces. More precisely, we present two conditions, each necessary and sufficient for a (real or complex) Banach space 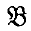to be isomorphic to the conjugate space of a Banach space, and two corresponding conditions for 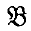to be equivalent to the conjugate space of a Banach space. Other characterizations, in terms of weak topologies, have been given by Alaoglu ((1), Theorem 2:1, p. 256, and Corollary 2:1, p. 257) and Bourbaki ((4), Chap, IV, §5, exerc. 15c, p. 122). Here, by the conjugate space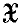* of a Banach space 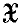we mean ((2), p. 188) the space of continuous linear functionals over 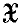. Two Banach spaces 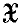and 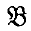are said to be isomorphic if there is a one-one continuous linear mapping of 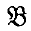onto 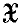(its inverse is necessarily continuous by the inversion theorem ((2), Théorème 5, p. 41; (6), Theorem 2·13·7, Corollary, p. 29)); they are said to be equivalent if there is a norm-preserving linear mapping of 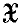onto 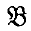.((2), p. 180).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 3 , July 1957 , pp. 576 - 580
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alaoglu, L.Weak topologies of normed linear spaces. Ann. Math., Princeton, (2) 41 (1940), 252–67.CrossRefGoogle Scholar
(2)Banach, S.Théorie des Opérations Linéaires (Warsaw, 1932).Google Scholar
(3)Bonsall, F. F.Dual extremum problems in the theory of functions. J. Lond. Math. Soc. 31 (1956), 105–10.CrossRefGoogle Scholar
(4)Bourbaki, N.Eléments de Mathématique, Fascicule XVIII [Espaces Vectoriels Topologiques, Chap, III–V et Dictionnaire] (Paris, 1955).Google Scholar
(4′)Dixmier, J.Sur un théorème de Banach. Duke Math. J. 15 (1948), 1057–71.CrossRefGoogle Scholar
(5)Grothendieck, A.Une caractérisation vectorielle-métrique des espaces L 1. Canad. J. Math. 7 (1955), 552–61.CrossRefGoogle Scholar
(6)Hille, E.Functional analysis and semi-groups (New York), 1948.Google Scholar
(7)Ruston, A. F.A short proof of a theorem on reflexive spaces. Proc. Camb. Phil. Soc. 45 (1949), 674.CrossRefGoogle Scholar
(8)Ruston, A. F.Direct products of Banach spaces and linear functional equations. Proc. Lond. Math. Soc. (3) 1 (1951), 327–84.CrossRefGoogle Scholar
(9)Schatten, R.A theory of cross-spaces (Princeton, 1950).Google Scholar