Let K be an algebraically closed field and 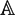$\mathbb{A}$n ≅ Kn affine n-space. It is known that a finite group 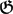$\frak{G}$ can only act freely on 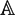$\mathbb{A}$n if K has characteristic p > 0 and 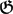$\frak{G}$ is a p-group. In that case the group action is “non-linear” and the ring of regular functions K[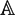$\mathbb{A}$n] must be a trace-surjectiveK − 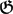$\frak{G}$-algebra.

Now let k be an arbitrary field of characteristic p > 0 and let G be a finite p-group. In this paper we study the category 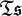$\mathfrak{Ts}$ of all finitely generated trace-surjective k − G algebras. It has been shown in [13] that the objects in 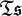$\mathfrak{Ts}$ are precisely those finitely generated k − G algebras A such that AG ≤ A is a Galois-extension in the sense of [7], with faithful action of G on A. Although 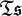$\mathfrak{Ts}$ is not an abelian category it has “s-projective objects”, which are analogues of projective modules, and it has (s-projective) categorical generators, which we will describe explicitly. We will show that s-projective objects and their rings of invariants are retracts of polynomial rings and therefore regular UFDs. The category 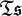$\mathfrak{Ts}$ also has “weakly initial objects”, which are closely related to the essential dimension of G over k. Our results yield a geometric structure theorem for free actions of finite p-groups on affine k-varieties. There are also close connections to open questions on retracts of polynomial rings, to embedding problems in standard modular Galois-theory of p-groups and, potentially, to a new constructive approach to homogeneous invariant theory.