Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-16T11:15:27.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals with a large parameter and several nearly coincident saddle points; the continuation of uniformly asymptotic expansions

Published online by Cambridge University Press:  24 October 2008

J. Martin
J. Martin
Affiliation:
Applied Mathematics, University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Abstract

In the contour integral

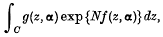
f and g are regular functions of z in a neighbourhood of the contour C and of the complex parameters (α1, α2, …, αp) = α in a domain of 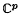. N is a positive parameter and asymptotic expansions are considered as N → + ∞. The method of steepest descents provides an asymptotic expansion for each fixed value of α, but this is non-uniform with respect to α near critical values α0 at which certain saddle points tend to coincidence. A more complicated expansion, involving Airy functions or generalizations thereof, is valid and uniform for α near α0. This expansion is known to be valid in a neighbourhood of α0 which does not depend on N, in contrast to certain other expansions having regions of validity which contract to a point or surface as N → ∞. It is thereby suggested that the actual region of validity has a definite geometrical shape determined by the functions f and g and the contour C, just as steepest descents expansions are valid in regions bounded by Stokes' lines. In this paper, procedures are derived for the determination of such regions, subject to assumptions concerning f, g and C. The validity of the expansion is established in regions so determined.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 76 , Issue 1 , July 1974 , pp. 211 - 231
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bleistein, N.Uniform asymptotic expansions of integrals with many nearby stationary points and algebraic singularities. J. Math. Mech. 17 (1967), 533–560.Google Scholar
(2)Burnside, W. S. & Panton, A. W.Theory of equations (Dublin; Longmans, 1904).Google Scholar
(3)Chester, C., Friedman, B. & Ursell, F.An extension of the method of steepest descents. Proc. Cambridge Philos. Soc. 53 (1957), 599–611.Google Scholar
(4)Jeffreys, H.Asymptotic approximations (Oxford, 1962).Google Scholar
(5)Levinson, N.Transformation of an analytic function of several variables to a canonical form. Duke Math. J. 28 (1961), 345–353.CrossRefGoogle Scholar
(6)Narasimhan, R.Several complex variables (Chicago, 1971).Google Scholar
(7)Ursell, F.Integrals with a large parameter. The continuation of uniformly asymptotic expansions. Proc. Cambridge Philos. Soc. 61 (1965), 113–128.Google Scholar
(8)Ursell, F.Integrals with a large parameter. Several nearly coincident saddle points. Proc. Cambridge Philos. Soc. 72 (1972), 49–65.Google Scholar