Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-28T23:13:50.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramanujan's Continued Fraction

Published online by Cambridge University Press:  24 October 2008

G. N. Watson
G. N. Watson
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The best of the theorems on continued fractions, to be found in Ramanujan's manuscript note-book may be stated as follows:

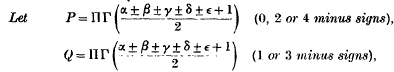
where there are eight gamma-functions in each product and the ambiguous signs are so chosen that the argument of each gamma-function contains one of the specified numbers of minus signs. Then

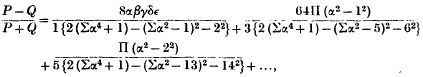
provided that one of the numbers β, γ δ, ε is equal to ± n, where n is a positive integer; and the products and sums on the right range over the numbers α β, γ δ, ε.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 1 , January 1935 , pp. 7 - 17
Copyright
Copyright © Cambridge Philosophical Society 1935

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Through an error in copying which occurred when I previously published an enunciation of the theorem, Journal London Math. Soc. 6 (1931), 146Google Scholar, the numbers in b 2 were inadvertently given as 9 and 10 instead of 13 and 14.

† Perron, O.. Die Lehre von den Kettenbrüchen (2. Aufl. 1929)Google Scholar.

* Hardy, G. H., “A chapter from Ramanujan's note-book”, Proc. Camb. Phil. Soc. 21 (1923), 492–503.Google Scholar

† Laguerre, E., “Sur la function ”, Bull. Soc. Math. France, 8 (1879), 36–52.Google Scholar

* Here and elsewhere it is supposed that the “numerators” and “denominators” of the convergents of a continued fraction are calculated without cancelling common factors, if such exist. Thus the numerators of the convergents of the continued fraction

are

* The properties of the original expressions show that their difference vanishes when α = 0, and so the difference contains α as a factor; similarly for β, γ, δ. Hence C n (α, β, γ, δ) is an integral function.