Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-21T06:07:04.463Z Has data issue: false hasContentIssue false
  • English
  • Français

A ‘stick-slip’ problem related to the motion of a free jet at low Reynolds numbers

Published online by Cambridge University Press:  24 October 2008

S. Richardson
S. Richardson
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Silver Street, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

A problem in fluid mechanics which has received some attention recently concerns the emergence of an incompressible Newtonian fluid jet from a uniform tube into an inviscid atmosphere. Both the axisymmetric case of a circular tube and the two-dimensional case of flow from between parallel planes are of interest. When the jet falls vertically under gravity, the motion far downstream is dominated by gravity and the expansion procedures of Clarke (3), and Kaye and Vale (10) give details of the flow in this region. When the flow near the exit is at a high Reynolds number, it is reasonable to expect the flow appropriate to that in an infinite tube to prevail right up to the exit (except, perhaps, near the point of discontinuity of the boundary conditions). With this assumption, Duda and Vrentas(5) use a numerical technique to solve for the flow in the axisymmetric jet beyond the exit, both with and without gravity acting in the axial direction. In the absence of gravity, the jet can be expected to attain a constant width some distance downstream, and at high Reynolds numbers the above assumption is sufficient to allow a mass and momentum balance to determine the contraction ratio of the jet as 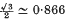for the axisymmetric case, and 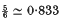for the two-dimensional case (see Harmon (8)). By treating the dynamics of the jet as those of a boundary layer growing on the free surface, Goren and Wronski (6) and Tillett (18) are able to examine the flow in greater detail.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 477 - 489
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Buchwald, V. T. and Doran, H. E.Proc. Roy. Soc. Ser. A 284 (1965), 69.Google Scholar
(2)Clarke, N. S. Asymptotic solutions displaying the effects of gravity and viscosity on certain flows with free boundaries. Ph.D. Dissertation, London University, 1966.Google Scholar
(3)Claeke, N. S.J. Fluid Mech. 31 (1968), 481.Google Scholar
(4)Doran, H. E. J.Austral. Math. Soc. 4 (1964), 342.CrossRefGoogle Scholar
(5)Duda, J. L. and Vrentas, J. S.Chem. Eng. Sci. 22 (1967), 855.CrossRefGoogle Scholar
(6)Goren, S. L. and Wronski, S. J.Fluid Mech. 25 (1966), 185.CrossRefGoogle Scholar
(7)Graebel, W. P.Phys. Fluids 8 (1965), 1929.CrossRefGoogle Scholar
(8)Harmon, D. B. J.Franklin Inst. 259 (1955), 519.Google Scholar
(9)Hillman, A. P. and Salzer, H. E.Philos. Mag. 34 (1943), 575.CrossRefGoogle Scholar
(10)Kaye, A. and Vale, D. G.Rheol. Acta 8 (1969), 1.CrossRefGoogle Scholar
(11)Michael, D. H.Mathematika 5 (1958), 82.CrossRefGoogle Scholar
(12)Middleman, S. and Gavis, J.Phys. Fluids 4 (1961), 355.CrossRefGoogle Scholar
(13)Moffatt, H. K.J. Fluid Mech. 18 (1964), 1.CrossRefGoogle Scholar
(14)Noble, B.Methods based on the Wiener-Hopf technique (Pergamon Press, 1958).Google Scholar
(15)Richardson, S. Slow viscous flows with free surfaces. Ph.D. Dissertation, Cambridge University, 1967.Google Scholar
(16)Richardson, S.J. Fluid Mech. 33 (1968), 475.CrossRefGoogle Scholar
(17)Riohardson, S.Rheol. Acta (1969), in press.Google Scholar
(18)Tillett, J. P. K.J. Fluid Mech. 32 (1968), 273.CrossRefGoogle Scholar
(19)Titchmarsh, E. C.The theory of Fourier integrals (Oxford University Press, 1962), Theorem 127.Google Scholar
(20)Titchmarsh, E. C.The theory of functions, p. 113 (Oxford University Press, 1964).Google Scholar
(21)Zidan, M.Rheol. Acta 8 (1969), 89.CrossRefGoogle Scholar