Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-17T16:33:10.186Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on finite differences with an application to the theory of Hausdorff summability

Published online by Cambridge University Press:  24 October 2008

W. H. J. Fuchs
W. H. J. Fuchs
Affiliation:
King's CollegeOld Aberdeen
Get access Rights & Permissions [Opens in a new window]

Extract

1. It is trivial that

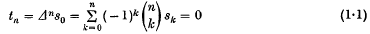
for all integers n ≥ 0 implies sn = 0 (n = 0, 1, 2, …). This conclusion is no longer true if it is only known that (1·1) is true for an infinity of n. But we shall show that the truth of (1·1) for, roughly speaking, one-half of all positive integers, together with an order condition on the magnitude of sn, ensures sn = 0 for all n. This follows from

Theorem 1. Let a1 < a2 < … be positive integers, n(R) the number of a's not exceeding R, sn a sequence of complex numbers. If

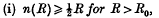
(ii) sn = ο(nK)as n tends to infinity

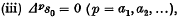
then sn = P(n), where P(x) is a polynomial of degree less than K.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 40 , Issue 2 , June 1944 , pp. 188 - 196
Copyright
Copyright © Cambridge Philosophical Society 1944

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Rogosinski, W. W., ‘On Hausdorff's methods of summability’, Proc. Cambridge Phil. Soc. 38 (1942), 166–92, Theorem 2.CrossRefGoogle Scholar

* Messenger of Math. 46 (1917), 175–82.Google Scholar See also Titchmarsh, , Theory of Fourier integrals (Oxford, 1937), p. 320.Google Scholar

* See, e.g., Paley-Wiener, , Fourier transforms in the complex domain (New York, 1934), pp. 68ff.Google Scholar

† Lindelöf, , Calcul des résidus (Paris, 1905), Ch. v, pp. 108ff.Google Scholar

* See Paley-Wiener, loc. cit., Theorem v.

† For a proof see, e.g., Banach, , Opérations linéaires, Ch. iv.Google Scholar