No CrossRef data available.
Article contents
ORTHOGONAL COLORINGS OF THE SPHERE
Published online by Cambridge University Press: 04 February 2016
Abstract
An orthogonal coloring of the two-dimensional unit sphere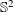 
$\mathbb{S}^{2}$, is a partition of 
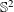$\mathbb{S}^{2}$ into parts such that no part contains a pair of orthogonal points: that is, a pair of points at spherical distance 
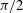${\it\pi}/2$ apart. It is a well-known result that an orthogonal coloring of 
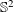$\mathbb{S}^{2}$ requires at least four parts, and orthogonal colorings with exactly four parts can easily be constructed from a regular octahedron centered at the origin. An intriguing question is whether or not every orthogonal 4-coloring of 
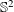$\mathbb{S}^{2}$ is such an octahedral coloring. In this paper, we address this question and show that if every color class has a non-empty interior, then the coloring is octahedral. Some related results are also given.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
Danzer, L., Grünbaum, B. and Klee, V., Helly’s theorem and its relatives. In Convexity
(Proceedings of Symposia in Pure Mathematics VII
), American Mathematical Society (Providence, RI, 1963).Google Scholar
Falconer, K. J., The realization of distances in measurable subsets covering R
n
. J. Combin. Theory Ser. A
31
1981, 184–189.CrossRefGoogle Scholar
Godsil, C. D. and Zaks, J., Colouring the sphere. Preprint, 2012, arXiv:1201.0486v1 [math.CO].Google Scholar
Kochen, S. and Specker, E. P., The problem of hidden variables in quantum mechanics. J. Math. Mech.
17
1967, 59–87.Google Scholar
Lee, S., Combinatorial Geometry on the Sphere. Master’s Thesis, KAIST, 2015.Google Scholar
Lovász, L., Self-dual polytopes and the chromatic number of distance graphs on the sphere. Acta Sci. Math.
45
1983, 317–323.Google Scholar
Noel, J., Partitioning the projective plane. http://mathoverflow.net/questions/140413/partitioning-the-projective-plane (2013).Google Scholar
Peres, A., Two simple proofs of the Kochen–Specker theorem. J. Phys. A: Math. Gen.
24
1991, L175–L178.Google Scholar
Raigorodskii, A. M., On the chromatic number of spheres in ℝ
n
. Combinatorica
32
2012, 111–123.Google Scholar
Raigorodskii, A. M., Coloring distance graphs and graphs of diameters. In Thirty Essays on Geometric Graph Theory (ed. Pach, J.), Springer (2013), 429–460.Google Scholar
Raigorodskii, A. M., Cliques and cycles in distance graphs and graphs of diameters. In Discrete geometry and Algebraic Combinatorics
(Contemporary Mathematics 625), American Mathematical Society (2014), 93–109.Google Scholar
Shelah, S. and Soifer, A., Axiom of choice and chromatic number of the plane. J. Combin. Theory Ser. A
103
2003, 387–391.Google Scholar
Shelah, S. and Soifer, A., Axiom of choice an chromatic number: examples on the plane. J. Combin. Theory Ser. A
105
2004, 359–364.Google Scholar
Simmons, G. J., The chromatic number of the sphere. J. Aust. Math. Soc.
21 (Series A) 1976, 473–480.Google Scholar
Soifer, A., The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators, Springer (Berlin, 2009).Google Scholar
Woodall, D. R., Distances realized by sets covering the plane. J. Combin. Theory Ser. A
14
1973, 187–200.Google Scholar