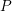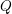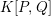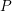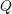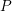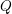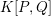1 Introduction
Let
![]() $K$
be a field, and let
$K$
be a field, and let
![]() $L$
be a finite distributive lattice. In 1987, Takayuki Hibi [Reference Hibi, Nagata and Matsumura11] introduced the
$L$
be a finite distributive lattice. In 1987, Takayuki Hibi [Reference Hibi, Nagata and Matsumura11] introduced the
![]() $K$
-algebra
$K$
-algebra
![]() $K[L]$
which nowadays is called the Hibi ring of the distributive lattice
$K[L]$
which nowadays is called the Hibi ring of the distributive lattice
![]() $L$
. The
$L$
. The
![]() $K$
-algebra
$K$
-algebra
![]() $K[L]$
is generated over
$K[L]$
is generated over
![]() $K$
by the elements
$K$
by the elements
![]() $\unicode[STIX]{x1D6FC}\in L$
with defining relations
$\unicode[STIX]{x1D6FC}\in L$
with defining relations
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FC}\vee \unicode[STIX]{x1D6FD})$
with
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D6FC}\vee \unicode[STIX]{x1D6FD})$
with
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in L$
. In the early paper, Hibi also showed that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in L$
. In the early paper, Hibi also showed that
![]() $K[L]$
is a normal Cohen–Macaulay domain.
$K[L]$
is a normal Cohen–Macaulay domain.
One remarkable fact is that
![]() $K[L]$
may be viewed as a toric ring. This can be seen by using Birkhoff’s fundamental theorem from 1937 which says that each finite distributive lattice is the ideal lattice of a finite poset
$K[L]$
may be viewed as a toric ring. This can be seen by using Birkhoff’s fundamental theorem from 1937 which says that each finite distributive lattice is the ideal lattice of a finite poset
![]() $P$
. Indeed, the subposet of
$P$
. Indeed, the subposet of
![]() $L$
, induced by the join-irreducible elements of
$L$
, induced by the join-irreducible elements of
![]() $L$
, is the poset
$L$
, is the poset
![]() $P$
whose ideal lattice
$P$
whose ideal lattice
![]() ${\mathcal{I}}(P)$
is the given distributive lattice
${\mathcal{I}}(P)$
is the given distributive lattice
![]() $L$
. Having the poset
$L$
. Having the poset
![]() $P$
of join-irreducible elements of
$P$
of join-irreducible elements of
![]() $L$
at our disposal, we can write
$L$
at our disposal, we can write
![]() $K[L]$
as the
$K[L]$
as the
![]() $K$
-algebra generated over
$K$
-algebra generated over
![]() $K$
by the monomials
$K$
by the monomials
![]() $u_{I}=\prod _{p\in I}x_{p}\prod _{p\not \in I}y_{p}\in K[\{x_{p},y_{p}\}_{p\in P}]$
with
$u_{I}=\prod _{p\in I}x_{p}\prod _{p\not \in I}y_{p}\in K[\{x_{p},y_{p}\}_{p\in P}]$
with
![]() $I\in {\mathcal{I}}(P)$
. Hibi, in his classical paper also showed that the Krull dimension of
$I\in {\mathcal{I}}(P)$
. Hibi, in his classical paper also showed that the Krull dimension of
![]() $K[L]$
is equal to
$K[L]$
is equal to
![]() $|P|+1$
, where
$|P|+1$
, where
![]() $|P|$
is the cardinality of
$|P|$
is the cardinality of
![]() $P$
.
$P$
.
Birkhoff’s theorem can also be phrased as follows: let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. We denote by
$Q$
be finite posets. We denote by
![]() $\operatorname{Hom}(P,Q)$
the set of order preserving maps, also called isotone maps. Observe that
$\operatorname{Hom}(P,Q)$
the set of order preserving maps, also called isotone maps. Observe that
![]() $\operatorname{Hom}(P,Q)$
is again a finite poset, by setting
$\operatorname{Hom}(P,Q)$
is again a finite poset, by setting
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
if and only if
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
if and only if
![]() $\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D713}(p)$
for all
$\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D713}(p)$
for all
![]() $p\in P$
. Let
$p\in P$
. Let
![]() $L$
be a distributive lattice with
$L$
be a distributive lattice with
![]() $P$
its subposet of join-irreducible elements. Birkhoff’s theorem is equivalent to saying that there is a natural isomorphism of posets
$P$
its subposet of join-irreducible elements. Birkhoff’s theorem is equivalent to saying that there is a natural isomorphism of posets
![]() $L\cong \operatorname{Hom}(P,[2])$
. Here for an integer
$L\cong \operatorname{Hom}(P,[2])$
. Here for an integer
![]() $n$
we denote by
$n$
we denote by
![]() $[n]$
the totally ordered set
$[n]$
the totally ordered set
![]() $\{1<2<\cdots <n\}$
.
$\{1<2<\cdots <n\}$
.
The set
![]() ${\mathcal{P}}$
of finite posets together with the isotone maps forms a category, first considered in [Reference Fløystad, Greve and Herzog6]. In the same paper the authors introduced the ideal
${\mathcal{P}}$
of finite posets together with the isotone maps forms a category, first considered in [Reference Fløystad, Greve and Herzog6]. In the same paper the authors introduced the ideal
![]() $L(P,Q)$
which is generated by the monomials
$L(P,Q)$
which is generated by the monomials
In the special cases when
![]() $P=[n]$
or
$P=[n]$
or
![]() $Q=[n]$
, the ideals
$Q=[n]$
, the ideals
![]() $L(P,Q)$
first appeared in the work [Reference Ene, Herzog and Mohammadi4] of Ene, Mohammadi and Jürgen Herzog. In the sequel the algebraic and homological properties of the ideals
$L(P,Q)$
first appeared in the work [Reference Ene, Herzog and Mohammadi4] of Ene, Mohammadi and Jürgen Herzog. In the sequel the algebraic and homological properties of the ideals
![]() $L(P,Q)$
have been subject of further investigations in the papers [Reference Herzog, Qureshi and Shikama10] and [Reference Juhnke-Kubitzke, Katthän and Madani14].
$L(P,Q)$
have been subject of further investigations in the papers [Reference Herzog, Qureshi and Shikama10] and [Reference Juhnke-Kubitzke, Katthän and Madani14].
Here we are interested in the algebras
![]() $K[P,Q]$
which are the toric rings generated over
$K[P,Q]$
which are the toric rings generated over
![]() $K$
by the monomials
$K$
by the monomials
![]() $u_{\unicode[STIX]{x1D711}}$
with
$u_{\unicode[STIX]{x1D711}}$
with
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
. We call these algebras isotonian because their generators are in bijection with the isotone maps from
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
. We call these algebras isotonian because their generators are in bijection with the isotone maps from
![]() $P$
to
$P$
to
![]() $Q$
. In the special case that
$Q$
. In the special case that
![]() $Q=[2]$
, we obtain the classical Hibi rings. Accordingly, one would expect that isotonian algebras share all the nice properties of Hibi rings. In Theorem 3.1 it is shown that
$Q=[2]$
, we obtain the classical Hibi rings. Accordingly, one would expect that isotonian algebras share all the nice properties of Hibi rings. In Theorem 3.1 it is shown that
![]() $\dim K[P,Q]=|P|(|Q|-s)+rs-r+1$
, where
$\dim K[P,Q]=|P|(|Q|-s)+rs-r+1$
, where
![]() $r$
is the number of connected components of
$r$
is the number of connected components of
![]() $P$
and
$P$
and
![]() $s$
is the number of connected components of
$s$
is the number of connected components of
![]() $Q$
. The proof of this theorem also shows that the algebraic variety whose coordinate ring is
$Q$
. The proof of this theorem also shows that the algebraic variety whose coordinate ring is
![]() $K[P,Q]$
is birationally equivalent to the Segre product of suitable copies of affine spaces.
$K[P,Q]$
is birationally equivalent to the Segre product of suitable copies of affine spaces.
Hibi rings are normal and Cohen–Macaulay. Do the same properties hold for isotonian algebras? In Corollary 4.3 it is shown that this is the case when the Hasse diagram of
![]() $P$
is a forest. But this is also the case when
$P$
is a forest. But this is also the case when
![]() $Q=[n]$
, as shown in [Reference Ene, Herzog and Mohammadi4, Corollary 4.3]. Corollary 4.3 is a straightforward consequence of a more general fact. Indeed, in Theorem 4.2 the following result is proved: let
$Q=[n]$
, as shown in [Reference Ene, Herzog and Mohammadi4, Corollary 4.3]. Corollary 4.3 is a straightforward consequence of a more general fact. Indeed, in Theorem 4.2 the following result is proved: let
![]() $P^{\prime }$
be the poset which is obtained from
$P^{\prime }$
be the poset which is obtained from
![]() $P$
by adding an element
$P$
by adding an element
![]() $p^{\prime }$
to
$p^{\prime }$
to
![]() $P$
which has a unique upper or lower neighbor in
$P$
which has a unique upper or lower neighbor in
![]() $P$
. Then
$P$
. Then
![]() $K[P,Q]$
is normal if and only if
$K[P,Q]$
is normal if and only if
![]() $K[P^{\prime },Q]$
is normal. Based on these results and on computational evidence we are lead to conjecture that all isotonian algebras are normal Cohen–Macaulay domains. One way to prove this conjecture in general would be to show that there exists a term order such that the initial ideal of the defining ideal
$K[P^{\prime },Q]$
is normal. Based on these results and on computational evidence we are lead to conjecture that all isotonian algebras are normal Cohen–Macaulay domains. One way to prove this conjecture in general would be to show that there exists a term order such that the initial ideal of the defining ideal
![]() $J_{P,Q}$
of
$J_{P,Q}$
of
![]() $K[P,Q]$
is squarefree. By a theorem of Sturmfels [Reference Sturmfels17, Chapter 8] this would imply that
$K[P,Q]$
is squarefree. By a theorem of Sturmfels [Reference Sturmfels17, Chapter 8] this would imply that
![]() $K[P,Q]$
is normal, and by a theorem of Hochster [Reference Hochster13, Theorem 1] this in turn implies Cohen–Macaulayness. In Theorem 5.5 we show that if
$K[P,Q]$
is normal, and by a theorem of Hochster [Reference Hochster13, Theorem 1] this in turn implies Cohen–Macaulayness. In Theorem 5.5 we show that if
![]() $P$
is a chain and
$P$
is a chain and
![]() $Q$
is a rooted or co-rooted poset, then
$Q$
is a rooted or co-rooted poset, then
![]() $J_{P,Q}$
has a quadratic (and hence also a squarefree) Gröbner basis with respect to the reverse lexicographic order induced by a canonical labeling of the variables. In general,
$J_{P,Q}$
has a quadratic (and hence also a squarefree) Gröbner basis with respect to the reverse lexicographic order induced by a canonical labeling of the variables. In general,
![]() $J_{P,Q}$
may contain generators of arbitrarily high degree. This happens if
$J_{P,Q}$
may contain generators of arbitrarily high degree. This happens if
![]() $Q$
contains as an induced subposet, what we call a poset cycle. On the other hand, we conjecture that
$Q$
contains as an induced subposet, what we call a poset cycle. On the other hand, we conjecture that
![]() $J_{P,Q}$
is quadratically generated if and only if
$J_{P,Q}$
is quadratically generated if and only if
![]() $Q$
does not contain any induced poset cycle of length greater than 4.
$Q$
does not contain any induced poset cycle of length greater than 4.
We would like to mention that Engström and Norén [Reference Engström and Norén5] introduced an algebra, associated to the set of homomorphisms between two finite graphs. While in our case the generators of the algebra correspond to the graph of isotone maps between posets, the generators of the Engström–Norén algebras correspond to the edge maps between the two given graphs. It is interesting that the classical Hibi rings, which are a very special case of isotonian algebras, allows also some interpretation in their theory, [Reference Engström and Norén5, Theorem 10.2]. Otherwise, though in spirit similar, the two theories are independent and disjoint.
2 Operations on posets and the
 $K$
-algebra
$K$
-algebra
 $K[P,Q]$
$K[P,Q]$
Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. A map
$Q$
be finite posets. A map
![]() $\unicode[STIX]{x1D711}:P\rightarrow Q$
is called isotone (order preserving), if
$\unicode[STIX]{x1D711}:P\rightarrow Q$
is called isotone (order preserving), if
![]() $\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D711}(p^{\prime })$
for all
$\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D711}(p^{\prime })$
for all
![]() $p,p^{\prime }\in P$
with
$p,p^{\prime }\in P$
with
![]() $p<p^{\prime }$
. The set of all isotone maps from
$p<p^{\prime }$
. The set of all isotone maps from
![]() $P$
to
$P$
to
![]() $Q$
is denoted by
$Q$
is denoted by
![]() $\operatorname{Hom}(P,Q)$
. Obviously, if
$\operatorname{Hom}(P,Q)$
. Obviously, if
![]() $P,Q$
and
$P,Q$
and
![]() $R$
are finite posets and
$R$
are finite posets and
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
and
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
and
![]() $\unicode[STIX]{x1D713}\in \operatorname{Hom}(Q,R)$
, then
$\unicode[STIX]{x1D713}\in \operatorname{Hom}(Q,R)$
, then
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in \operatorname{Hom}(P,R)$
. We denote by
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in \operatorname{Hom}(P,R)$
. We denote by
![]() ${\mathcal{P}}$
the category whose objects are finite posets and whose morphisms are isotone maps. We note that
${\mathcal{P}}$
the category whose objects are finite posets and whose morphisms are isotone maps. We note that
![]() $\operatorname{Hom}(P,Q)$
is again a poset with
$\operatorname{Hom}(P,Q)$
is again a poset with
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
for
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
for
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in \operatorname{Hom}(P,Q)$
if and only if
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in \operatorname{Hom}(P,Q)$
if and only if
![]() $\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D713}(p)$
for all
$\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D713}(p)$
for all
![]() $p\in P$
. Thus,
$p\in P$
. Thus, ![]() is a covariant and
is a covariant and ![]() a contravariant functor.
a contravariant functor.
Let
![]() $P\in {\mathcal{P}}$
, and let
$P\in {\mathcal{P}}$
, and let
![]() $p_{1},p_{2}\in P$
. One says that
$p_{1},p_{2}\in P$
. One says that
![]() $p_{2}$
covers
$p_{2}$
covers
![]() $p_{1}$
if
$p_{1}$
if
![]() $p_{1}<p_{2}$
, and there is no
$p_{1}<p_{2}$
, and there is no
![]() $p\in P$
with
$p\in P$
with
![]() $p_{1}<p<p_{2}$
. We define the graph
$p_{1}<p<p_{2}$
. We define the graph
![]() $G(P)$
on the vertex set
$G(P)$
on the vertex set
![]() $P$
as follows: a
$P$
as follows: a
![]() $2$
-element subset
$2$
-element subset
![]() $\{p_{1},p_{2}\}$
is an edge of
$\{p_{1},p_{2}\}$
is an edge of
![]() $G(P)$
if and only if
$G(P)$
if and only if
![]() $p_{2}$
covers
$p_{2}$
covers
![]() $p_{1}$
or
$p_{1}$
or
![]() $p_{1}$
covers
$p_{1}$
covers
![]() $p_{2}$
. The graph
$p_{2}$
. The graph
![]() $G(P)$
is the underlying graph of the so-called Hasse diagram of
$G(P)$
is the underlying graph of the so-called Hasse diagram of
![]() $P$
which may be viewed as a directed graph whose edges are the ordered pairs
$P$
which may be viewed as a directed graph whose edges are the ordered pairs
![]() $(p_{1},p_{2})$
, where
$(p_{1},p_{2})$
, where
![]() $p_{2}$
covers
$p_{2}$
covers
![]() $p_{1}$
.
$p_{1}$
.
We say that
![]() $P$
is connected, if
$P$
is connected, if
![]() $G(P)$
is a connected graph. Given two posets
$G(P)$
is a connected graph. Given two posets
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
, the sum
$P_{2}$
, the sum
![]() $P_{1}+P_{2}$
is defined to be the disjoint union of the elements of
$P_{1}+P_{2}$
is defined to be the disjoint union of the elements of
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
with
$P_{2}$
with
![]() $p\leqslant q$
if and only if
$p\leqslant q$
if and only if
![]() $p,q\in P_{1}$
or
$p,q\in P_{1}$
or
![]() $p,q\in P_{2}$
and
$p,q\in P_{2}$
and
![]() $p\leqslant q$
in the corresponding posets
$p\leqslant q$
in the corresponding posets
![]() $P_{1}$
or
$P_{1}$
or
![]() $P_{2}$
. Then it is clear that any
$P_{2}$
. Then it is clear that any
![]() $P\in {\mathcal{P}}$
can be written as
$P\in {\mathcal{P}}$
can be written as
![]() $P=\sum _{i=1}^{r}P_{i}$
where each
$P=\sum _{i=1}^{r}P_{i}$
where each
![]() $P_{i}$
is a connected subposet of
$P_{i}$
is a connected subposet of
![]() $P$
. The subposets
$P$
. The subposets
![]() $P_{i}$
of
$P_{i}$
of
![]() $P$
are called the connected components of
$P$
are called the connected components of
![]() $P$
.
$P$
.
Example 2.1. Let
![]() $P$
be the poset displayed in Figure 1.
$P$
be the poset displayed in Figure 1.
We identify an isotone map
![]() $\unicode[STIX]{x1D711}:P\rightarrow P$
with
$\unicode[STIX]{x1D711}:P\rightarrow P$
with
![]() $\unicode[STIX]{x1D711}(p_{i})=p_{j_{i}}$
(
$\unicode[STIX]{x1D711}(p_{i})=p_{j_{i}}$
(
![]() $i=1,2,3$
) with the sequence
$i=1,2,3$
) with the sequence
![]() $j_{1}j_{2}j_{3}$
. With the notation introduced, the elements of
$j_{1}j_{2}j_{3}$
. With the notation introduced, the elements of
![]() $\operatorname{Hom}(P,P)$
are:
$\operatorname{Hom}(P,P)$
are:
The poset
![]() $\operatorname{Hom}(P,P)$
is displayed in Figure 2.
$\operatorname{Hom}(P,P)$
is displayed in Figure 2.
The product
![]() $P_{1}\times P_{2}$
of
$P_{1}\times P_{2}$
of
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
is the poset whose elements are the pairs
$P_{2}$
is the poset whose elements are the pairs
![]() $(p_{1},p_{2})$
with
$(p_{1},p_{2})$
with
![]() $p_{1}\in P_{1}$
and
$p_{1}\in P_{1}$
and
![]() $p_{2}\in P_{2}$
. The order relations in
$p_{2}\in P_{2}$
. The order relations in
![]() $P_{1}\times P_{2}$
are defined componentwise. For
$P_{1}\times P_{2}$
are defined componentwise. For
![]() $P_{1}\times P_{2}\times \cdots \times P_{s}$
we also write
$P_{1}\times P_{2}\times \cdots \times P_{s}$
we also write
![]() $\prod _{i=1}^{s}P_{i}$
.
$\prod _{i=1}^{s}P_{i}$
.
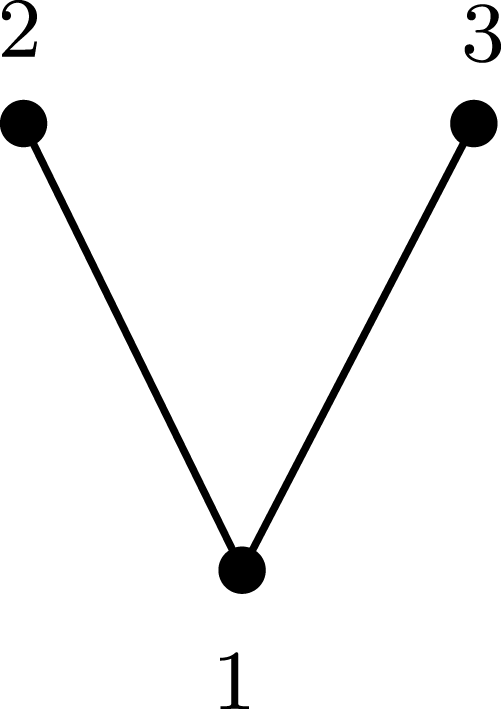
Figure 1. Poset
![]() $P$
.
$P$
.
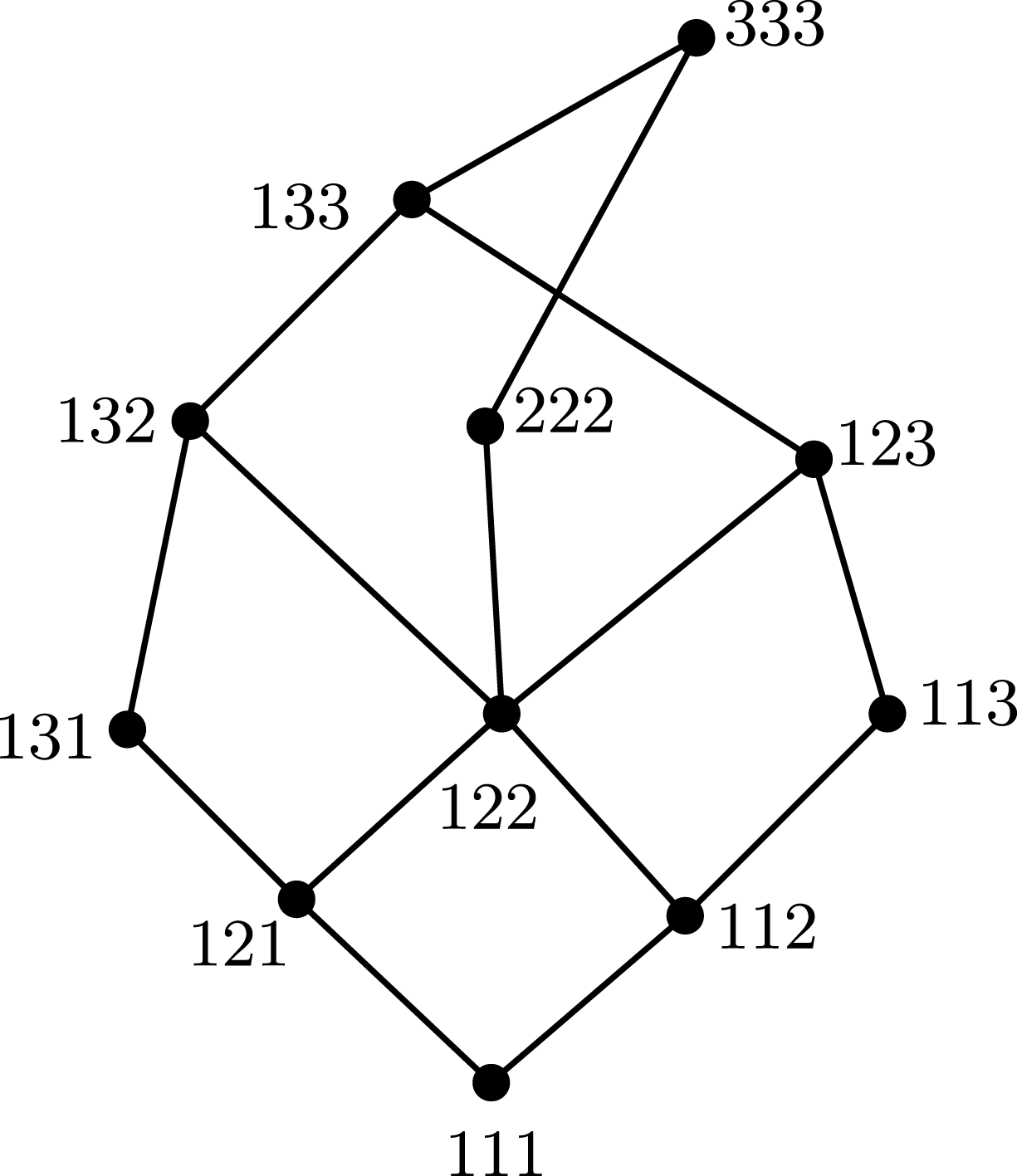
Figure 2.
![]() $\operatorname{Hom}(P,P)$
.
$\operatorname{Hom}(P,P)$
.
In the next lemma we present two obvious (but useful) rules of the
![]() $\operatorname{Hom}$
-posets.
$\operatorname{Hom}$
-posets.
Lemma 2.2. Let
![]() $P,P_{1},P_{2},\ldots ,P_{r}$
and
$P,P_{1},P_{2},\ldots ,P_{r}$
and
![]() $Q,Q_{1},Q_{2},\ldots ,Q_{s}$
be finite posets, and assume that
$Q,Q_{1},Q_{2},\ldots ,Q_{s}$
be finite posets, and assume that
![]() $P$
is connected. Then:
$P$
is connected. Then:
(a)
 $\operatorname{Hom}(\sum _{i=1}^{r}P_{i},Q)\cong \prod _{i=1}^{r}\operatorname{Hom}(P_{i},Q)$
;
$\operatorname{Hom}(\sum _{i=1}^{r}P_{i},Q)\cong \prod _{i=1}^{r}\operatorname{Hom}(P_{i},Q)$
;(b)
 $\operatorname{Hom}(P,\sum _{i=1}^{s}Q_{i})\cong \sum _{i=1}^{s}\operatorname{Hom}(P,Q_{i})$
.
$\operatorname{Hom}(P,\sum _{i=1}^{s}Q_{i})\cong \sum _{i=1}^{s}\operatorname{Hom}(P,Q_{i})$
.
We now introduce the isotonian algebra
![]() $K[P,Q]$
attached to a pair
$K[P,Q]$
attached to a pair
![]() $P$
,
$P$
,
![]() $Q$
of finite posets. For this purpose we fix a field
$Q$
of finite posets. For this purpose we fix a field
![]() $K$
, and consider the polynomial ring over
$K$
, and consider the polynomial ring over
![]() $K$
in the variables
$K$
in the variables
![]() $x_{p,q}$
with
$x_{p,q}$
with
![]() $p\in P$
and
$p\in P$
and
![]() $q\in Q$
. Then
$q\in Q$
. Then
![]() $K[P,Q]$
is the toric ring generated over
$K[P,Q]$
is the toric ring generated over
![]() $K$
by the monomials
$K$
by the monomials
Let
![]() $R_{1}=K[f_{1},\ldots ,f_{r}]\subset K[x_{1},\ldots ,x_{n}]$
and
$R_{1}=K[f_{1},\ldots ,f_{r}]\subset K[x_{1},\ldots ,x_{n}]$
and
![]() $R_{2}=K[g_{1},\ldots ,g_{s}]\subset K[y_{1},\ldots ,y_{m}]$
be two standard graded
$R_{2}=K[g_{1},\ldots ,g_{s}]\subset K[y_{1},\ldots ,y_{m}]$
be two standard graded
![]() $K$
-algebras. Then
$K$
-algebras. Then
is the tensor product of
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
over
$R_{2}$
over
![]() $K$
, while
$K$
, while
is the Segre product of
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
.
$R_{2}$
.
The following isomorphisms are immediate consequences of Lemma 2.2 and the definition of isotonian algebras.
Lemma 2.3. Let
![]() $P,P_{1},P_{2},\ldots ,P_{r}$
and
$P,P_{1},P_{2},\ldots ,P_{r}$
and
![]() $Q,Q_{1},Q_{2},\ldots ,Q_{s}$
be finite posets and assume that
$Q,Q_{1},Q_{2},\ldots ,Q_{s}$
be finite posets and assume that
![]() $P$
is connected. Then:
$P$
is connected. Then:
(a)
 $K[\sum _{i=1}^{r}P_{i},Q]\cong K[P_{1},Q]\ast K[P_{2},Q]\ast \cdots \ast K[P_{r},Q]$
;
$K[\sum _{i=1}^{r}P_{i},Q]\cong K[P_{1},Q]\ast K[P_{2},Q]\ast \cdots \ast K[P_{r},Q]$
;(b)
 $K[P,\sum _{i=1}^{s}Q_{i}]\cong K[P,Q_{1}]\otimes K[P,Q_{2}]\otimes \cdots \otimes K[P,Q_{s}]$
.
$K[P,\sum _{i=1}^{s}Q_{i}]\cong K[P,Q_{1}]\otimes K[P,Q_{2}]\otimes \cdots \otimes K[P,Q_{s}]$
.
As a first consequence we obtain
Corollary 2.4. Let
![]() $P$
be a finite poset with connected components
$P$
be a finite poset with connected components
![]() $P_{1},P_{2},\ldots ,P_{r}$
and let
$P_{1},P_{2},\ldots ,P_{r}$
and let
![]() $Q$
be a finite poset with connected components
$Q$
be a finite poset with connected components
![]() $Q_{1},Q_{2},\ldots ,Q_{s}$
. Then
$Q_{1},Q_{2},\ldots ,Q_{s}$
. Then
![]() $K[P,Q]$
is normal if all
$K[P,Q]$
is normal if all
![]() $K[P_{i},Q_{j}]$
are normal. In particular, if this is the case, then
$K[P_{i},Q_{j}]$
are normal. In particular, if this is the case, then
![]() $K[P,Q]$
is also Cohen–Macaulay.
$K[P,Q]$
is also Cohen–Macaulay.
Proof. It is a well-known fact that the Segre product or the tensor product of normal standard graded toric rings is normal. Thus the assertion follows. The Cohen–Macaulayness of
![]() $K[P,Q]$
is then the consequence of Hochster’s theorem [Reference Hochster13, Theorem 1].◻
$K[P,Q]$
is then the consequence of Hochster’s theorem [Reference Hochster13, Theorem 1].◻
Let
![]() $P\in {\mathcal{P}}$
. The dual poset
$P\in {\mathcal{P}}$
. The dual poset
![]() $P^{\vee }$
of
$P^{\vee }$
of
![]() $P$
is the poset whose underlying set coincides with that of
$P$
is the poset whose underlying set coincides with that of
![]() $P$
and whose order relations are reversed. In other words,
$P$
and whose order relations are reversed. In other words,
![]() $p<p^{\prime }$
in
$p<p^{\prime }$
in
![]() $P$
is equivalent to
$P$
is equivalent to
![]() $p^{\prime }<p$
in
$p^{\prime }<p$
in
![]() $P^{\vee }$
.
$P^{\vee }$
.
Since
![]() $\unicode[STIX]{x1D711}:P\rightarrow Q$
is isotone if and only if
$\unicode[STIX]{x1D711}:P\rightarrow Q$
is isotone if and only if
![]() $\unicode[STIX]{x1D711}:P^{\vee }\rightarrow Q^{\vee }$
is isotone, we have
$\unicode[STIX]{x1D711}:P^{\vee }\rightarrow Q^{\vee }$
is isotone, we have
Lemma 2.5. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. Then the
$Q$
be finite posets. Then the
![]() $K$
-algebras
$K$
-algebras
![]() $K[P,Q]$
and
$K[P,Q]$
and
![]() $K[P^{\vee },Q^{\vee }]$
are isomorphic.
$K[P^{\vee },Q^{\vee }]$
are isomorphic.
3 The dimension of
 $K[P,Q]$
$K[P,Q]$
In this section we compute the dimension of the algebra
![]() $K[P,Q]$
. The result is given in
$K[P,Q]$
. The result is given in
Theorem 3.1. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets and let
$Q$
be finite posets and let
![]() $r$
be the number of connected components of
$r$
be the number of connected components of
![]() $P$
and
$P$
and
![]() $s$
be the number of connected components of
$s$
be the number of connected components of
![]() $Q$
. Then
$Q$
. Then
![]() $\dim K[P,Q]=|P|(|Q|-s)+rs-r+1$
.
$\dim K[P,Q]=|P|(|Q|-s)+rs-r+1$
.
Proof. By using Lemma 2.3 and the fact that for any two standard graded
![]() $K$
-algebras
$K$
-algebras
![]() $R$
and
$R$
and
![]() $S$
,
$S$
,
![]() $\dim R\otimes S=\dim R+\dim S$
and
$\dim R\otimes S=\dim R+\dim S$
and
![]() $\dim R\ast S=\dim R+\dim S-1$
(see [Reference Goto and Watanabe7, Theorem 4.2.3]), the desired conclusion follows once we have shown that
$\dim R\ast S=\dim R+\dim S-1$
(see [Reference Goto and Watanabe7, Theorem 4.2.3]), the desired conclusion follows once we have shown that
![]() $\dim K[P,Q]=|P|(|Q|-1)+1$
in the case that
$\dim K[P,Q]=|P|(|Q|-1)+1$
in the case that
![]() $P$
and
$P$
and
![]() $Q$
are connected. Let
$Q$
are connected. Let
![]() $L$
be the quotient field of
$L$
be the quotient field of
![]() $K[P,Q]$
. Since
$K[P,Q]$
. Since
![]() $K[P,Q]$
is an affine domain, the
$K[P,Q]$
is an affine domain, the
![]() $\dim K[P,Q]$
is the transcendence degree of
$\dim K[P,Q]$
is the transcendence degree of
![]() $L/K$
.
$L/K$
.
Let
![]() $L^{\prime }$
be the field generated by the elements:
$L^{\prime }$
be the field generated by the elements:
(i)
 $u_{q}=\prod _{p\in P}x_{p,q}$
for
$u_{q}=\prod _{p\in P}x_{p,q}$
for
 $q\in Q$
;
$q\in Q$
;(ii)
 $x_{p,q}/x_{p,q^{\prime }}$
for
$x_{p,q}/x_{p,q^{\prime }}$
for
 $p\in P$
,
$p\in P$
,
 $q,q^{\prime }\in Q$
and
$q,q^{\prime }\in Q$
and
 $q<q^{\prime }$
.
$q<q^{\prime }$
.
We show that
![]() $L^{\prime }=L$
. It is obvious that elements
$L^{\prime }=L$
. It is obvious that elements
![]() $u_{q}$
belong to
$u_{q}$
belong to
![]() $L$
. Let
$L$
. Let
![]() $I$
be any poset ideal of
$I$
be any poset ideal of
![]() $P$
and let
$P$
and let
![]() $q,q^{\prime }\in Q$
with
$q,q^{\prime }\in Q$
with
![]() $q<q^{\prime }$
. Then
$q<q^{\prime }$
. Then
![]() $\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}:P\rightarrow Q$
defined by
$\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}:P\rightarrow Q$
defined by
is an isotone map with image
![]() $\{q,q^{\prime }\}$
. Given any
$\{q,q^{\prime }\}$
. Given any
![]() $p_{0}\in P$
, one can find two poset ideals
$p_{0}\in P$
, one can find two poset ideals
![]() $I,J$
of
$I,J$
of
![]() $P$
such that
$P$
such that
![]() $J=I\cup \{p_{0}\}$
and
$J=I\cup \{p_{0}\}$
and
![]() $p_{0}\notin I$
. Then
$p_{0}\notin I$
. Then
![]() $u_{\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}}=\prod _{p\in I}x_{p,q}\prod _{p\notin I}x_{p,q^{\prime }}$
and
$u_{\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}}=\prod _{p\in I}x_{p,q}\prod _{p\notin I}x_{p,q^{\prime }}$
and
![]() $u_{\unicode[STIX]{x1D711}_{J}^{(q,q^{\prime })}}=(\prod _{p\in I}x_{p,q})x_{p_{0},q}(\prod _{p\notin I}x_{p,q^{\prime }})x_{p_{0},q^{\prime }}^{-1}$
. It follows that
$u_{\unicode[STIX]{x1D711}_{J}^{(q,q^{\prime })}}=(\prod _{p\in I}x_{p,q})x_{p_{0},q}(\prod _{p\notin I}x_{p,q^{\prime }})x_{p_{0},q^{\prime }}^{-1}$
. It follows that
![]() $u_{\unicode[STIX]{x1D711}_{J}^{(q,q^{\prime })}}/u_{\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}}=x_{p_{0},q}/x_{p_{0},q^{\prime }}$
. It shows that all elements in (ii) belong to
$u_{\unicode[STIX]{x1D711}_{J}^{(q,q^{\prime })}}/u_{\unicode[STIX]{x1D711}_{I}^{(q,q^{\prime })}}=x_{p_{0},q}/x_{p_{0},q^{\prime }}$
. It shows that all elements in (ii) belong to
![]() $L$
. Therefore,
$L$
. Therefore,
![]() $L^{\prime }\subset L$
.
$L^{\prime }\subset L$
.
In order to prove the converse inclusion, let
![]() $P=\{p_{1},\ldots ,p_{n}\}$
and let
$P=\{p_{1},\ldots ,p_{n}\}$
and let
![]() $q_{1},\ldots ,q_{n}$
be arbitrary elements in
$q_{1},\ldots ,q_{n}$
be arbitrary elements in
![]() $Q$
. We show by induction on
$Q$
. We show by induction on
![]() $k$
that the monomial
$k$
that the monomial
![]() $x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{k+1}}\cdots x_{p_{n},q_{n}}$
can be obtained as a product of
$x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{k+1}}\cdots x_{p_{n},q_{n}}$
can be obtained as a product of
![]() $x_{p_{1},q_{1}}\cdots x_{p_{n},q_{n}}$
and suitable elements in (ii) and their inverses. This will imply that any monomial generator of
$x_{p_{1},q_{1}}\cdots x_{p_{n},q_{n}}$
and suitable elements in (ii) and their inverses. This will imply that any monomial generator of
![]() $K[P,Q]$
is contained in
$K[P,Q]$
is contained in
![]() $L^{\prime }$
, because the element
$L^{\prime }$
, because the element
![]() $x_{p_{1},q_{1}}x_{p_{2},q_{2}}\cdots x_{p_{n},q_{n}}$
can then be written as a product of
$x_{p_{1},q_{1}}x_{p_{2},q_{2}}\cdots x_{p_{n},q_{n}}$
can then be written as a product of
![]() $x_{p_{1},q_{1}}\cdots x_{p_{n},q_{1}}$
and elements of type (ii) and their inverses. As a consequence this will imply that
$x_{p_{1},q_{1}}\cdots x_{p_{n},q_{1}}$
and elements of type (ii) and their inverses. As a consequence this will imply that
![]() $L\subset L^{\prime }$
.
$L\subset L^{\prime }$
.
For
![]() $k=1$
, the statement is trivial. Since
$k=1$
, the statement is trivial. Since
![]() $Q$
is connected, there exists a sequence of elements
$Q$
is connected, there exists a sequence of elements
![]() $\tilde{q}_{1},\ldots ,\tilde{q}_{t}$
in
$\tilde{q}_{1},\ldots ,\tilde{q}_{t}$
in
![]() $Q$
with
$Q$
with
![]() $\tilde{q}_{1}=q_{1}$
and
$\tilde{q}_{1}=q_{1}$
and
![]() $\tilde{q}_{t}=q_{k+1}$
and
$\tilde{q}_{t}=q_{k+1}$
and
![]() $\tilde{q}_{i}$
and
$\tilde{q}_{i}$
and
![]() $\tilde{q}_{i+1}$
are comparable for all
$\tilde{q}_{i+1}$
are comparable for all
![]() $i$
in
$i$
in
![]() $Q$
. Then
$Q$
. Then
where each
![]() $x_{p_{k+1},\tilde{q}_{i}}/x_{p_{k+1},\tilde{q}_{i+1}}$
or its inverse is a monomial of type (ii). Then the monomial
$x_{p_{k+1},\tilde{q}_{i}}/x_{p_{k+1},\tilde{q}_{i+1}}$
or its inverse is a monomial of type (ii). Then the monomial
![]() $x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{1}}x_{p_{k+2},q_{k+2}}\cdots x_{p_{n},q_{n}}$
can be obtained as a product of the monomial
$x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{1}}x_{p_{k+2},q_{k+2}}\cdots x_{p_{n},q_{n}}$
can be obtained as a product of the monomial
![]() $x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{k+1}}\cdots x_{p_{n},q_{n}}$
and the monomial
$x_{p_{1},q_{1}}\cdots x_{p_{k},q_{1}}x_{p_{k+1},q_{k+1}}\cdots x_{p_{n},q_{n}}$
and the monomial
![]() $x_{p_{k+1},q_{1}}/x_{p_{k+1},q_{k+1}}$
.
$x_{p_{k+1},q_{1}}/x_{p_{k+1},q_{k+1}}$
.
Let
![]() $T$
be a spanning tree (i.e., a maximal tree) of
$T$
be a spanning tree (i.e., a maximal tree) of
![]() $G(Q)$
and choose an element
$G(Q)$
and choose an element
![]() $p_{0}\in P$
. Next we show that
$p_{0}\in P$
. Next we show that
![]() $L$
is generated by the elements:
$L$
is generated by the elements:
- (i)
 $u_{q}=\prod _{p\in P}x_{p,q}$
, for
$u_{q}=\prod _{p\in P}x_{p,q}$
, for
 $q\in Q$
;
$q\in Q$
;- (ii
 $^{\prime }$
)
$^{\prime }$
)  $x_{p,q}/x_{p,q^{\prime }}$
for
$x_{p,q}/x_{p,q^{\prime }}$
for
 $p\in P\setminus \{p_{0}\}$
and
$p\in P\setminus \{p_{0}\}$
and
 $\{q,q^{\prime }\}\in E(T)$
with
$\{q,q^{\prime }\}\in E(T)$
with
 $q<q^{\prime }$
;
$q<q^{\prime }$
;
where
![]() $E(T)$
is the edge set of
$E(T)$
is the edge set of
![]() $T$
. For any
$T$
. For any
![]() $q<q^{\prime }$
in
$q<q^{\prime }$
in
![]() $Q$
, we can obtain a sequence
$Q$
, we can obtain a sequence
![]() $\tilde{q_{1}},\ldots ,\tilde{q_{t}}$
in
$\tilde{q_{1}},\ldots ,\tilde{q_{t}}$
in
![]() $T$
such that
$T$
such that
![]() $\tilde{q_{1}}=q$
and
$\tilde{q_{1}}=q$
and
![]() $\tilde{q_{t}}=q^{\prime }$
and
$\tilde{q_{t}}=q^{\prime }$
and
![]() $\tilde{q_{i}}$
and
$\tilde{q_{i}}$
and
![]() $\tilde{q}_{i+1}$
are neighbors for all
$\tilde{q}_{i+1}$
are neighbors for all
![]() $i=1,\ldots ,t$
. Consequently, we obtain
$i=1,\ldots ,t$
. Consequently, we obtain
Also note that
![]() $x_{p_{0},q}/x_{p_{0},q^{\prime }}=(u_{q}/u_{q^{\prime }})(\prod _{p\in P\setminus \{p_{0}\}}(x_{p,q^{\prime }}/x_{p,q}))$
for
$x_{p_{0},q}/x_{p_{0},q^{\prime }}=(u_{q}/u_{q^{\prime }})(\prod _{p\in P\setminus \{p_{0}\}}(x_{p,q^{\prime }}/x_{p,q}))$
for
![]() $q<q^{\prime }$
, and hence
$q<q^{\prime }$
, and hence
![]() $x_{p_{0},q}/x_{p_{0},q^{\prime }}$
is a product of elements of type (i) and (ii
$x_{p_{0},q}/x_{p_{0},q^{\prime }}$
is a product of elements of type (i) and (ii
![]() $^{\prime }$
) and their inverses. This shows that all monomials of type (ii) can be obtained as product of monomials of type (i) and type (ii
$^{\prime }$
) and their inverses. This shows that all monomials of type (ii) can be obtained as product of monomials of type (i) and type (ii
![]() $^{\prime }$
) and their inverses.
$^{\prime }$
) and their inverses.
Let
![]() ${\mathcal{A}}$
be the set of exponent vectors (in
${\mathcal{A}}$
be the set of exponent vectors (in
![]() $\mathbb{Q}^{P\times Q}$
) of the monomials of type (i) and
$\mathbb{Q}^{P\times Q}$
) of the monomials of type (i) and
![]() ${\mathcal{B}}$
be the set of exponent vectors of the monomials of type (ii
${\mathcal{B}}$
be the set of exponent vectors of the monomials of type (ii
![]() $^{\prime }$
). We show the set of vectors
$^{\prime }$
). We show the set of vectors
![]() ${\mathcal{A}}\cup {\mathcal{B}}$
is linearly independent. Then [Reference Villarreal18, Proposition 7.1.17] implies that the Krull dimension of
${\mathcal{A}}\cup {\mathcal{B}}$
is linearly independent. Then [Reference Villarreal18, Proposition 7.1.17] implies that the Krull dimension of
![]() $K[P,Q]$
is equal to the cardinality of the set
$K[P,Q]$
is equal to the cardinality of the set
![]() ${\mathcal{A}}\cup {\mathcal{B}}$
.
${\mathcal{A}}\cup {\mathcal{B}}$
.
Note that vectors in
![]() ${\mathcal{A}}$
are linearly independent because their support is pairwise disjoint. Also, the vectors in
${\mathcal{A}}$
are linearly independent because their support is pairwise disjoint. Also, the vectors in
![]() ${\mathcal{B}}$
are linearly independent. To see this, we let
${\mathcal{B}}$
are linearly independent. To see this, we let
![]() ${\mathcal{B}}_{p}\subset {\mathcal{B}}$
be the set of exponent vectors of monomials
${\mathcal{B}}_{p}\subset {\mathcal{B}}$
be the set of exponent vectors of monomials
![]() $x_{p,q}/x_{p,q^{\prime }}$
in (ii
$x_{p,q}/x_{p,q^{\prime }}$
in (ii
![]() $^{\prime }$
) with
$^{\prime }$
) with
![]() $p$
fixed. Then
$p$
fixed. Then
![]() ${\mathcal{B}}$
is the disjoint union of the sets
${\mathcal{B}}$
is the disjoint union of the sets
![]() ${\mathcal{B}}_{p}$
with
${\mathcal{B}}_{p}$
with
![]() $p\in P\setminus \{p_{0}\}$
. Moreover, for distinct
$p\in P\setminus \{p_{0}\}$
. Moreover, for distinct
![]() $p,p^{\prime }\in P\setminus \{p_{0}\}$
the vectors in
$p,p^{\prime }\in P\setminus \{p_{0}\}$
the vectors in
![]() ${\mathcal{B}}_{p}$
and
${\mathcal{B}}_{p}$
and
![]() ${\mathcal{B}}_{p^{\prime }}$
have disjoint support. Thus it suffices to show that for a fixed
${\mathcal{B}}_{p^{\prime }}$
have disjoint support. Thus it suffices to show that for a fixed
![]() $p\in P\setminus \{p_{0}\}$
the vectors in
$p\in P\setminus \{p_{0}\}$
the vectors in
![]() ${\mathcal{B}}_{p}$
are linearly independent. Now we fix such
${\mathcal{B}}_{p}$
are linearly independent. Now we fix such
![]() $p\in P\setminus \{p_{0}\}$
. Then the matrix formed by the vectors of
$p\in P\setminus \{p_{0}\}$
. Then the matrix formed by the vectors of
![]() ${\mathcal{B}}_{p}$
is the incidence matrix of the tree
${\mathcal{B}}_{p}$
is the incidence matrix of the tree
![]() $T$
which is known to be of maximal rank (see for example [Reference Villarreal18, Lemma 8.3.2]). Thus the vectors of
$T$
which is known to be of maximal rank (see for example [Reference Villarreal18, Lemma 8.3.2]). Thus the vectors of
![]() ${\mathcal{B}}_{p}$
are linearly independent, as desired.
${\mathcal{B}}_{p}$
are linearly independent, as desired.
Finally, to show that
![]() ${\mathcal{A}}\cup {\mathcal{B}}$
is a set of linearly independent vectors it suffices to show
${\mathcal{A}}\cup {\mathcal{B}}$
is a set of linearly independent vectors it suffices to show
![]() $V\cap W=\{0\}$
, where
$V\cap W=\{0\}$
, where
![]() $V$
is the
$V$
is the
![]() $\mathbb{Q}$
-vector space spanned by
$\mathbb{Q}$
-vector space spanned by
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() $W$
is the
$W$
is the
![]() $\mathbb{Q}$
-vector space spanned by
$\mathbb{Q}$
-vector space spanned by
![]() ${\mathcal{B}}$
. Thus we have to show that if
${\mathcal{B}}$
. Thus we have to show that if
![]() $v\in V$
and
$v\in V$
and
![]() $w\in W$
with
$w\in W$
with
![]() $v=w$
, then
$v=w$
, then
![]() $v=w=0$
. This is equivalent to say that if
$v=w=0$
. This is equivalent to say that if
![]() $u$
is a product of elements of (i) and its inverses and
$u$
is a product of elements of (i) and its inverses and
![]() $u^{\prime }$
is a product of elements of (ii
$u^{\prime }$
is a product of elements of (ii
![]() $^{\prime }$
) and its inverses, and if
$^{\prime }$
) and its inverses, and if
![]() $u=u^{\prime }$
, then
$u=u^{\prime }$
, then
![]() $u=u^{\prime }=1$
. This is indeed the case, because if
$u=u^{\prime }=1$
. This is indeed the case, because if
![]() $u\neq 1$
, then
$u\neq 1$
, then
![]() $u$
contains factors of the form
$u$
contains factors of the form
![]() $x_{p_{0},q}$
, while
$x_{p_{0},q}$
, while
![]() $u^{\prime }$
does not.
$u^{\prime }$
does not.
Now we determine the cardinality of
![]() ${\mathcal{A}}\cup {\mathcal{B}}$
(which coincides with
${\mathcal{A}}\cup {\mathcal{B}}$
(which coincides with
![]() $\dim K[P,Q]$
). Observe that
$\dim K[P,Q]$
). Observe that
![]() $|{\mathcal{A}}|=|Q|$
and
$|{\mathcal{A}}|=|Q|$
and
![]() $|{\mathcal{B}}|=(|P|-1)(|Q|-1)$
, so that
$|{\mathcal{B}}|=(|P|-1)(|Q|-1)$
, so that
![]() $|{\mathcal{A}}\cup {\mathcal{B}}|=(|P|-1)(|Q|-1)+|Q|=|P|(|Q|-1)+1$
.◻
$|{\mathcal{A}}\cup {\mathcal{B}}|=(|P|-1)(|Q|-1)+|Q|=|P|(|Q|-1)+1$
.◻
Corollary 3.2. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite connected posets with
$Q$
be finite connected posets with
![]() $|P|=n$
and
$|P|=n$
and
![]() $|Q|=m$
, and let
$|Q|=m$
, and let
![]() $X_{P,Q}$
be the irreducible variety given by the defining ideal
$X_{P,Q}$
be the irreducible variety given by the defining ideal
![]() $J_{P,Q}$
of
$J_{P,Q}$
of
![]() $K[P,Q]$
. Then
$K[P,Q]$
. Then
![]() $X_{P,Q}$
is birationally equivalent to the variety
$X_{P,Q}$
is birationally equivalent to the variety
![]() $Y_{n,m}$
whose coordinate ring is the
$Y_{n,m}$
whose coordinate ring is the
![]() $n$
-fold Segre product of the
$n$
-fold Segre product of the
![]() $m$
-dimensional polynomial ring over
$m$
-dimensional polynomial ring over
![]() $K$
.
$K$
.
Proof. Let
![]() $P=\{p_{1},\ldots ,p_{n}\}$
, and let
$P=\{p_{1},\ldots ,p_{n}\}$
, and let
![]() $L$
be the quotient field of
$L$
be the quotient field of
![]() $K[P,Q]$
and
$K[P,Q]$
and
![]() $T$
be the toric ring whose generators are of the form
$T$
be the toric ring whose generators are of the form
![]() $\prod _{j=1}^{n}x_{p_{j},q_{j}}$
with
$\prod _{j=1}^{n}x_{p_{j},q_{j}}$
with
![]() $q_{j}\in Q$
. Note that
$q_{j}\in Q$
. Note that
where
![]() $S_{i}=K[x_{p_{i},q}:q\in Q]$
for
$S_{i}=K[x_{p_{i},q}:q\in Q]$
for
![]() $i=1,\ldots ,n$
. It was shown in the proof of Theorem 3.1 that
$i=1,\ldots ,n$
. It was shown in the proof of Theorem 3.1 that
![]() $L$
is also the quotient field of
$L$
is also the quotient field of
![]() $T$
. This yields the desired conclusion.◻
$T$
. This yields the desired conclusion.◻
4 Normality of
 $K[P,Q]$
$K[P,Q]$
In this section we prove normality of
![]() $K[P,Q]$
in certain cases. As
$K[P,Q]$
in certain cases. As
![]() $K[P,Q]$
is a toric ring, normality of
$K[P,Q]$
is a toric ring, normality of
![]() $K[P,Q]$
, by a theorem of Hochster [Reference Hochster13, Theorem 1], implies that
$K[P,Q]$
, by a theorem of Hochster [Reference Hochster13, Theorem 1], implies that
![]() $K[P,Q]$
is Cohen–Macaulay as well.
$K[P,Q]$
is Cohen–Macaulay as well.
Let
![]() $H$
be an affine semigroup and
$H$
be an affine semigroup and
![]() $\mathbb{Z}H$
be the associated group of
$\mathbb{Z}H$
be the associated group of
![]() $H$
. The semigroup
$H$
. The semigroup
![]() $H$
is normal, if whenever
$H$
is normal, if whenever
![]() $da\in H$
for
$da\in H$
for
![]() $a\in \mathbb{Z}H$
and some
$a\in \mathbb{Z}H$
and some
![]() $d\in \mathbb{N}$
, then
$d\in \mathbb{N}$
, then
![]() $a\in H$
. By [Reference Bruns and Herzog2, Theorem 6.1.4],
$a\in H$
. By [Reference Bruns and Herzog2, Theorem 6.1.4],
![]() $K[H]$
is normal if and only if
$K[H]$
is normal if and only if
![]() $H$
is normal. We apply this criterion to
$H$
is normal. We apply this criterion to
![]() $K[P,Q]$
. Since
$K[P,Q]$
. Since
![]() $K[P,Q]$
is a toric ring, there exists an affine semigroup
$K[P,Q]$
is a toric ring, there exists an affine semigroup
![]() $H$
such that
$H$
such that
![]() $K[H]=K[P,Q]$
. It follows that
$K[H]=K[P,Q]$
. It follows that
![]() $K[P,Q]$
is normal if and only if
$K[P,Q]$
is normal if and only if
![]() $H$
is normal. In our particular situation, when
$H$
is normal. In our particular situation, when
![]() $P=\{p_{1},\ldots ,p_{n}\}$
, the monomials in
$P=\{p_{1},\ldots ,p_{n}\}$
, the monomials in
![]() $K[\mathbb{Z}H]$
corresponding to the elements in
$K[\mathbb{Z}H]$
corresponding to the elements in
![]() $\mathbb{Z}H$
are of the form
$\mathbb{Z}H$
are of the form
![]() $u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}$
with
$u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}$
with
![]() $u_{i}=x_{p_{1},q_{i1}}x_{p_{2},q_{i2}}\cdots x_{p_{n},q_{in}}$
for
$u_{i}=x_{p_{1},q_{i1}}x_{p_{2},q_{i2}}\cdots x_{p_{n},q_{in}}$
for
![]() $i=1,\ldots ,s$
,
$i=1,\ldots ,s$
,
![]() $s\geqslant 1$
and
$s\geqslant 1$
and
![]() $q_{ij}\in Q$
. Thus it will follow that
$q_{ij}\in Q$
. Thus it will follow that
![]() $K[P,Q]$
is normal if whenever
$K[P,Q]$
is normal if whenever
![]() $(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}\in K[P,Q]$
, then
$(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}\in K[P,Q]$
, then
![]() $u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}\in K[P,Q]$
.
$u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}\in K[P,Q]$
.
Lemma 4.1. Let
![]() $P,Q$
be two finite posets with
$P,Q$
be two finite posets with
![]() $P=\{p_{1},\ldots ,p_{n}\}$
, and let as before
$P=\{p_{1},\ldots ,p_{n}\}$
, and let as before
![]() $S_{i}=K[x_{p_{i},q}:q\in Q]$
for
$S_{i}=K[x_{p_{i},q}:q\in Q]$
for
![]() $i=1,\ldots ,n$
. Assume that for any integer
$i=1,\ldots ,n$
. Assume that for any integer
![]() $d>1$
and any sequence of monomials
$d>1$
and any sequence of monomials
![]() $v_{1},\ldots ,v_{t}\in S_{1}\ast S_{2}\ast \cdots \ast S_{n}$
with
$v_{1},\ldots ,v_{t}\in S_{1}\ast S_{2}\ast \cdots \ast S_{n}$
with
![]() $(v_{1}v_{2}\cdots v_{t})^{d}\in K[P,Q]$
it follows that
$(v_{1}v_{2}\cdots v_{t})^{d}\in K[P,Q]$
it follows that
![]() $v_{1}v_{2}\cdots v_{t}\in K[P,Q]$
. Then the toric ring
$v_{1}v_{2}\cdots v_{t}\in K[P,Q]$
. Then the toric ring
![]() $K[P,Q]$
is normal.
$K[P,Q]$
is normal.
Proof. Suppose
![]() $(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}\in K[P,Q]$
. We show that there exist monomials
$(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}\in K[P,Q]$
. We show that there exist monomials
![]() $v_{1},\ldots ,v_{t}\in S_{1}\ast S_{2}\ast \cdots \ast S_{n}$
such that
$v_{1},\ldots ,v_{t}\in S_{1}\ast S_{2}\ast \cdots \ast S_{n}$
such that
![]() $(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}=(v_{1}\cdots v_{t})^{d}$
. Then our assumption implies that
$(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}=(v_{1}\cdots v_{t})^{d}$
. Then our assumption implies that
![]() $v_{1}\cdots v_{t}\in K[P,Q]$
. Since
$v_{1}\cdots v_{t}\in K[P,Q]$
. Since
![]() $(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}=(v_{1}\cdots v_{t})^{d}$
and since
$(u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1})^{d}=(v_{1}\cdots v_{t})^{d}$
and since
![]() $K[P,Q]$
is a toric ring, we have
$K[P,Q]$
is a toric ring, we have
![]() $u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}=v_{1}\cdots v_{t}$
, and so the desired conclusion follows.
$u_{1}^{\pm 1}u_{2}^{\pm 1}\cdots u_{s}^{\pm 1}=v_{1}\cdots v_{t}$
, and so the desired conclusion follows.
Without loss of generality we may assume that
for some
![]() $r\leqslant s$
. Let
$r\leqslant s$
. Let
![]() $u_{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}}$
for
$u_{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}}$
for
![]() $1\leqslant i\leqslant s$
. Then
$1\leqslant i\leqslant s$
. Then
belongs to
![]() $K[P,Q]$
. Since the elements in
$K[P,Q]$
. Since the elements in
![]() $K[P,Q]$
have no negative powers, it follows that each factor in
$K[P,Q]$
have no negative powers, it follows that each factor in
![]() $\prod _{k=1}^{r}x_{p_{i},q_{ki}}^{-d}$
cancels against a factor in
$\prod _{k=1}^{r}x_{p_{i},q_{ki}}^{-d}$
cancels against a factor in
![]() $\prod _{k=r+1}^{s}x_{p_{i},q_{ki}}^{d}$
. Without loss of generality we may assume that for each
$\prod _{k=r+1}^{s}x_{p_{i},q_{ki}}^{d}$
. Without loss of generality we may assume that for each
![]() $i$
,
$i$
,
![]() $\prod _{k=1}^{r}x_{p_{i},q_{ki}}^{-d}$
cancels against
$\prod _{k=1}^{r}x_{p_{i},q_{ki}}^{-d}$
cancels against
![]() $\prod _{k=r+1}^{2r}x_{p_{i},q_{ki}}^{d}$
. Then
$\prod _{k=r+1}^{2r}x_{p_{i},q_{ki}}^{d}$
. Then
where
![]() $v_{j}=\prod _{i=1}^{n}x_{p_{i},q_{2r+j,i}}$
.◻
$v_{j}=\prod _{i=1}^{n}x_{p_{i},q_{2r+j,i}}$
.◻
Based on the criterion given in Lemma 4.1 we show
Theorem 4.2. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets, and let
$Q$
be finite posets, and let
![]() $P^{\prime }$
be a poset which is obtained from
$P^{\prime }$
be a poset which is obtained from
![]() $P$
by adding an element
$P$
by adding an element
![]() $p^{\prime }$
to
$p^{\prime }$
to
![]() $P$
with the property that
$P$
with the property that
![]() $p^{\prime }$
has a unique neighbor in
$p^{\prime }$
has a unique neighbor in
![]() $G(P^{\prime })$
. Then
$G(P^{\prime })$
. Then
![]() $K[P^{\prime },Q]$
is normal if and only if
$K[P^{\prime },Q]$
is normal if and only if
![]() $K[P,Q]$
is normal.
$K[P,Q]$
is normal.
Proof. By Corollary 2.4 we may assume that
![]() $P$
is connected. Let
$P$
is connected. Let
![]() $P=\{p_{1},\ldots ,p_{n}\}$
and set
$P=\{p_{1},\ldots ,p_{n}\}$
and set
![]() $p_{n+1}=p^{\prime }$
. We may assume that
$p_{n+1}=p^{\prime }$
. We may assume that
![]() $p_{n}$
is the unique neighbor of
$p_{n}$
is the unique neighbor of
![]() $p_{n+1}$
in
$p_{n+1}$
in
![]() $G(P)$
and that
$G(P)$
and that
![]() $p_{n}<p_{n+1}$
. In other words,
$p_{n}<p_{n+1}$
. In other words,
![]() $p_{n}$
is the unique element in
$p_{n}$
is the unique element in
![]() $P$
covered by
$P$
covered by
![]() $p_{n+1}$
.
$p_{n+1}$
.
Suppose first that
![]() $K[P^{\prime },Q]$
is normal but
$K[P^{\prime },Q]$
is normal but
![]() $K[P,Q]$
is not normal. Then there exist monomials
$K[P,Q]$
is not normal. Then there exist monomials
![]() $u_{1},\ldots ,u_{s}\in S_{1}\ast \cdots \ast S_{n}$
such that
$u_{1},\ldots ,u_{s}\in S_{1}\ast \cdots \ast S_{n}$
such that
![]() $(u_{1}\cdots u_{s})^{d}\in K[P,Q]$
but
$(u_{1}\cdots u_{s})^{d}\in K[P,Q]$
but
![]() $u_{1}\cdots u_{s}\not \in K[P,Q]$
.
$u_{1}\cdots u_{s}\not \in K[P,Q]$
.
We write
![]() $\unicode[STIX]{x1D711}_{i}$
for the (not necessarily isotone) map
$\unicode[STIX]{x1D711}_{i}$
for the (not necessarily isotone) map
![]() $P\rightarrow Q$
corresponding to
$P\rightarrow Q$
corresponding to
![]() $u_{i}$
, and define the map
$u_{i}$
, and define the map
![]() $\unicode[STIX]{x1D711}_{i}^{\prime }:P^{\prime }\rightarrow Q$
by setting
$\unicode[STIX]{x1D711}_{i}^{\prime }:P^{\prime }\rightarrow Q$
by setting
Let
![]() $u_{i}^{\prime }$
be the monomial corresponding to
$u_{i}^{\prime }$
be the monomial corresponding to
![]() $\unicode[STIX]{x1D711}_{i}^{\prime }$
. Then we have
$\unicode[STIX]{x1D711}_{i}^{\prime }$
. Then we have
![]() $(u_{1}^{\prime }\cdots u_{s}^{\prime })^{d}\in K[P^{\prime },Q]$
but
$(u_{1}^{\prime }\cdots u_{s}^{\prime })^{d}\in K[P^{\prime },Q]$
but
![]() $u_{1}^{\prime }\cdots u_{s}^{\prime }\not \in K[P^{\prime },Q]$
, a contradiction.
$u_{1}^{\prime }\cdots u_{s}^{\prime }\not \in K[P^{\prime },Q]$
, a contradiction.
Conversely, suppose that
![]() $K[P,Q]$
is normal. Let
$K[P,Q]$
is normal. Let
![]() $u_{1},\ldots ,u_{s}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
$u_{1},\ldots ,u_{s}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
![]() $u_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}}$
for
$u_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}}$
for
![]() $i=1,\ldots ,s$
. By Lemma 4.1 it is enough to show that if
$i=1,\ldots ,s$
. By Lemma 4.1 it is enough to show that if
![]() $(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
for some
$(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
for some
![]() $d\in \mathbb{N}$
, then
$d\in \mathbb{N}$
, then
![]() $u_{1}u_{2}\cdots u_{s}\in K[P^{\prime },Q]$
.
$u_{1}u_{2}\cdots u_{s}\in K[P^{\prime },Q]$
.
In order to prove this, we first observe that
![]() $\unicode[STIX]{x1D711}:P^{\prime }\rightarrow Q$
is isotone, if and only if
$\unicode[STIX]{x1D711}:P^{\prime }\rightarrow Q$
is isotone, if and only if
![]() $\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D711}(q)$
for all pairs
$\unicode[STIX]{x1D711}(p)\leqslant \unicode[STIX]{x1D711}(q)$
for all pairs
![]() $p,q\in P^{\prime }$
for which
$p,q\in P^{\prime }$
for which
![]() $q$
covers
$q$
covers
![]() $p$
. Hence,
$p$
. Hence,
![]() $\unicode[STIX]{x1D711}:P^{\prime }\rightarrow Q$
is isotone if and only if the restriction of
$\unicode[STIX]{x1D711}:P^{\prime }\rightarrow Q$
is isotone if and only if the restriction of
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $P$
is isotone and
$P$
is isotone and
![]() $\unicode[STIX]{x1D711}(p_{n})\leqslant \unicode[STIX]{x1D711}(p_{n+1})$
.
$\unicode[STIX]{x1D711}(p_{n})\leqslant \unicode[STIX]{x1D711}(p_{n+1})$
.
As a consequence of this observation we obtain the following statement: let
![]() $v_{1},\ldots ,v_{t}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
$v_{1},\ldots ,v_{t}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
![]() $v_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}^{\prime }}$
for
$v_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}^{\prime }}$
for
![]() $i=1,\ldots ,t$
, and set
$i=1,\ldots ,t$
, and set
![]() $\tilde{v}_{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}^{\prime }}$
for
$\tilde{v}_{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}^{\prime }}$
for
![]() $i=1,\ldots ,t$
. Then
$i=1,\ldots ,t$
. Then
![]() $v_{1}\cdots v_{t}\in K[P^{\prime },Q]$
if and only if:
$v_{1}\cdots v_{t}\in K[P^{\prime },Q]$
if and only if:
(i)
 $\tilde{v}_{1}\cdots \tilde{v}_{t}\in K[P,Q]$
;
$\tilde{v}_{1}\cdots \tilde{v}_{t}\in K[P,Q]$
;(ii) there exists a permutation
 $\unicode[STIX]{x1D70B}:[t]\rightarrow [t]$
such that
$\unicode[STIX]{x1D70B}:[t]\rightarrow [t]$
such that
 $q_{in}^{\prime }\leqslant q_{\unicode[STIX]{x1D70B}(i),n+1}^{\prime }$
for all
$q_{in}^{\prime }\leqslant q_{\unicode[STIX]{x1D70B}(i),n+1}^{\prime }$
for all
 $i$
.
$i$
.
Condition (ii) can be rephrased as follows: let
![]() $G$
be the bipartite graph with bipartition
$G$
be the bipartite graph with bipartition
![]() $V(G)=V_{1}\cup V_{2}$
, where
$V(G)=V_{1}\cup V_{2}$
, where
![]() $V_{1}=\{x_{1},\ldots ,x_{t}\}$
and
$V_{1}=\{x_{1},\ldots ,x_{t}\}$
and
![]() $V_{2}=\{y_{1},\ldots ,y_{t}\}$
. We let
$V_{2}=\{y_{1},\ldots ,y_{t}\}$
. We let
![]() $\{x_{i},y_{j}\}$
be an edge of
$\{x_{i},y_{j}\}$
be an edge of
![]() $G$
if and only if
$G$
if and only if
![]() $q_{in}^{\prime }\leqslant q_{j,n+1}^{\prime }$
. We call
$q_{in}^{\prime }\leqslant q_{j,n+1}^{\prime }$
. We call
![]() $G$
the graph attached to
$G$
the graph attached to
![]() $v_{1},\ldots ,v_{t}$
. By definition, a perfect matching of
$v_{1},\ldots ,v_{t}$
. By definition, a perfect matching of
![]() $G$
is a disjoint union of
$G$
is a disjoint union of
![]() $t$
edges of
$t$
edges of
![]() $G$
.
$G$
.
Now condition (ii) is equivalent to the following condition:
- (ii
 $^{\prime }$
)
$^{\prime }$
) The graph
 $G$
attached to
$G$
attached to
 $v_{1},\ldots ,v_{t}$
admits a perfect matching.
$v_{1},\ldots ,v_{t}$
admits a perfect matching.
Now we come back to the sequence
![]() $u_{1},\ldots ,u_{s}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
$u_{1},\ldots ,u_{s}\in S_{1}\ast S_{1}\ast \cdots \ast S_{n+1}$
with
![]() $u_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}}$
for
$u_{i}=\prod _{j=1}^{n+1}x_{p_{j},q_{ij}}$
for
![]() $i=1,\ldots ,s$
for which
$i=1,\ldots ,s$
for which
![]() $(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
.
$(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
.
Then (i) implies that
![]() $(\tilde{u} _{1}\cdots \tilde{u} _{s})^{d}\in K[P,Q]$
. By assumption,
$(\tilde{u} _{1}\cdots \tilde{u} _{s})^{d}\in K[P,Q]$
. By assumption,
![]() $K[P,Q]$
is normal. This implies that
$K[P,Q]$
is normal. This implies that
![]() $\tilde{u} _{1}\cdots \tilde{u} _{s}\in K[P,Q]$
, where
$\tilde{u} _{1}\cdots \tilde{u} _{s}\in K[P,Q]$
, where
![]() $\tilde{u} _{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}}$
. Thus it will follow that
$\tilde{u} _{i}=\prod _{j=1}^{n}x_{p_{j},q_{ij}}$
. Thus it will follow that
![]() $u_{1}\cdots u_{s}\in K[P^{\prime },Q]$
if the graph
$u_{1}\cdots u_{s}\in K[P^{\prime },Q]$
if the graph
![]() $G$
attached to
$G$
attached to
![]() $u_{1},\ldots ,u_{s}$
admits a perfect matching.
$u_{1},\ldots ,u_{s}$
admits a perfect matching.
We let
![]() $G^{(d)}$
be the graph attached to
$G^{(d)}$
be the graph attached to
![]() $d$
copies of
$d$
copies of
![]() $u_{1},\ldots ,u_{s}$
:
$u_{1},\ldots ,u_{s}$
:
Since
![]() $(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
it follows from (ii
$(u_{1}u_{2}\cdots u_{s})^{d}\in K[P^{\prime },Q]$
it follows from (ii
![]() $^{\prime }$
) that
$^{\prime }$
) that
![]() $G^{(d)}$
admits a perfect matching.
$G^{(d)}$
admits a perfect matching.
Note that
![]() $G^{(d)}$
may be viewed as the bipartite graph with vertex decomposition
$G^{(d)}$
may be viewed as the bipartite graph with vertex decomposition
where
The edges of
![]() $G^{(d)}$
are
$G^{(d)}$
are
![]() $\{x_{i}^{(k)},y_{j}^{(l)}\}$
with
$\{x_{i}^{(k)},y_{j}^{(l)}\}$
with
![]() $q_{in}\leqslant q_{j,n+1}$
and
$q_{in}\leqslant q_{j,n+1}$
and
![]() $k,l\in [d]$
.
$k,l\in [d]$
.
Suppose that
![]() $G$
has no perfect matching. Then Hall’s marriage theorem (see for example [Reference Herzog and Hibi9, Lemma 9.1.2]) implies that there exists a set
$G$
has no perfect matching. Then Hall’s marriage theorem (see for example [Reference Herzog and Hibi9, Lemma 9.1.2]) implies that there exists a set
![]() $S\subset V_{1}$
such that
$S\subset V_{1}$
such that
![]() $|N_{G}(S)|<|S|$
. Here
$|N_{G}(S)|<|S|$
. Here
is the set of neighbors of
![]() $S$
.
$S$
.
Let
![]() $S^{(d)}=\{x_{i}^{(k)}:x_{i}\in S,1\leqslant k\leqslant d\}$
. Then
$S^{(d)}=\{x_{i}^{(k)}:x_{i}\in S,1\leqslant k\leqslant d\}$
. Then
![]() $S^{(d)}\subset V_{1}^{(d)}$
and
$S^{(d)}\subset V_{1}^{(d)}$
and
Thus,
![]() $G^{(d)}$
does not have a perfect matching, a contradiction.◻
$G^{(d)}$
does not have a perfect matching, a contradiction.◻
By using Theorem 4.2 and an obvious induction argument, we obtain
Corollary 4.3. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. Then
$Q$
be finite posets. Then
![]() $K[P,Q]$
is a normal Cohen–Macaulay domain if
$K[P,Q]$
is a normal Cohen–Macaulay domain if
![]() $G(P)$
is a tree.
$G(P)$
is a tree.
Corollary 4.3 implies in particular that
![]() $K[[n],Q]$
is normal. On the other hand, the normality of
$K[[n],Q]$
is normal. On the other hand, the normality of
![]() $K[P,[n]]$
has been proved in [Reference Ene, Herzog and Mohammadi4, Corollary 4.2]. These types of algebras are called letterplace algebras. Thus we have
$K[P,[n]]$
has been proved in [Reference Ene, Herzog and Mohammadi4, Corollary 4.2]. These types of algebras are called letterplace algebras. Thus we have
Corollary 4.4. All letterplace algebras are normal Cohen–Macaulay domains.
It seems that
![]() $K[P,Q]$
is normal, not only when
$K[P,Q]$
is normal, not only when
![]() $G(P)$
is a tree. For example, it can be shown by using Normaliz [Reference Bruns, Ichim and Söger3] that the isotonian algebra
$G(P)$
is a tree. For example, it can be shown by using Normaliz [Reference Bruns, Ichim and Söger3] that the isotonian algebra
![]() $K[Q,Q]$
is normal for the poset
$K[Q,Q]$
is normal for the poset
![]() $Q$
shown in Figure 3.
$Q$
shown in Figure 3.
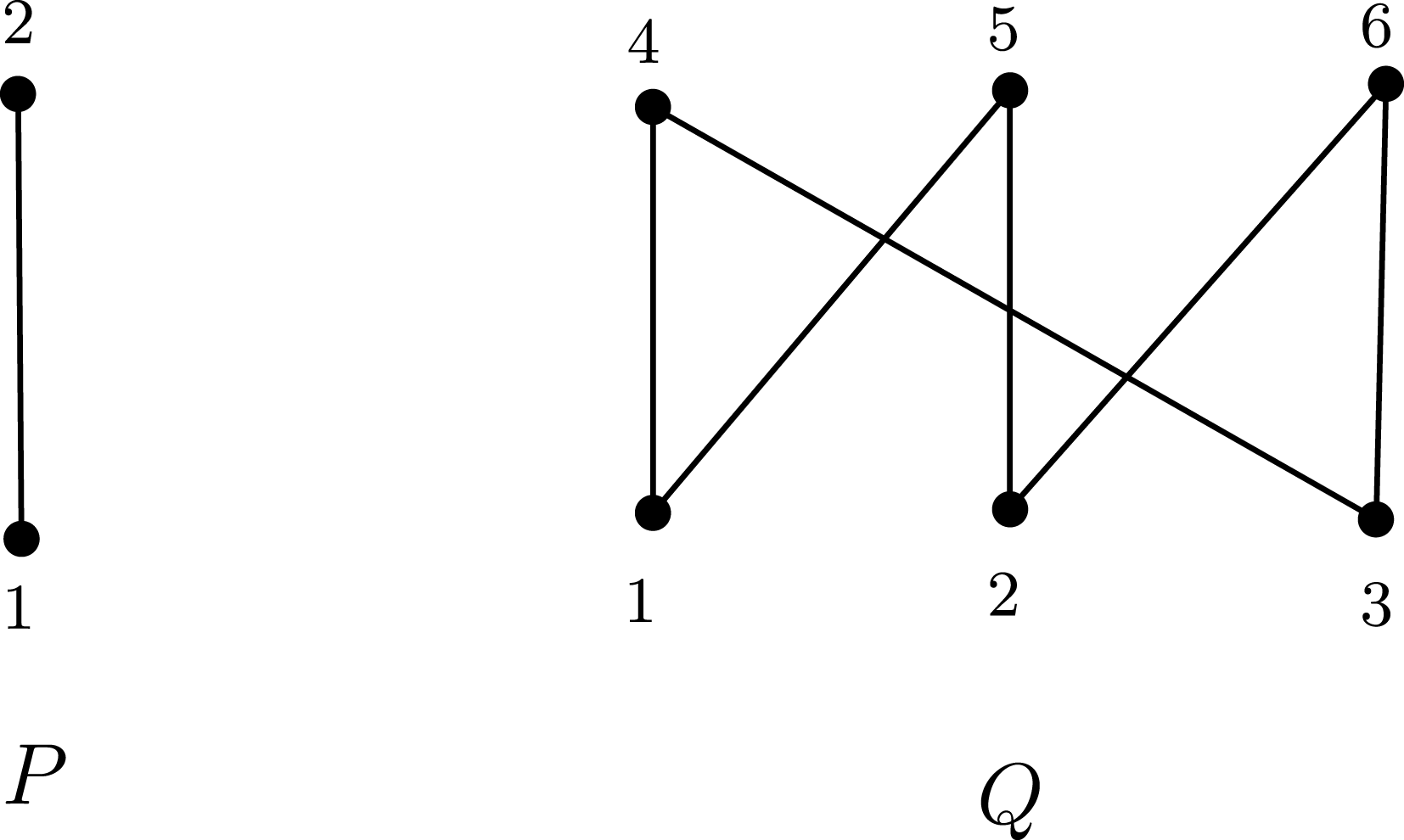
Figure 3.
![]() $J_{P,Q}$
is not quadratic.
$J_{P,Q}$
is not quadratic.
Further computational evidence and the above special cases lead us to the following
Conjecture 4.5. Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. Then
$Q$
be finite posets. Then
![]() $K[P,Q]$
is a normal Cohen–Macaulay domain.
$K[P,Q]$
is a normal Cohen–Macaulay domain.
5 Gröbner basis
Let
![]() $P$
and
$P$
and
![]() $Q$
be finite posets. Let
$Q$
be finite posets. Let
![]() $S=K[y_{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)]$
be the polynomial ring in the variables
$S=K[y_{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)]$
be the polynomial ring in the variables
![]() $y_{\unicode[STIX]{x1D711}}$
, and let
$y_{\unicode[STIX]{x1D711}}$
, and let
![]() $\unicode[STIX]{x1D70B}:S\rightarrow K[P,Q]$
be the
$\unicode[STIX]{x1D70B}:S\rightarrow K[P,Q]$
be the
![]() $K$
-algebra homomorphism defined by
$K$
-algebra homomorphism defined by
![]() $y_{\unicode[STIX]{x1D711}}\mapsto \prod _{p\in P}x_{p,\unicode[STIX]{x1D711}(p)}$
. We denote the kernel of
$y_{\unicode[STIX]{x1D711}}\mapsto \prod _{p\in P}x_{p,\unicode[STIX]{x1D711}(p)}$
. We denote the kernel of
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
![]() $J_{P,Q}$
.
$J_{P,Q}$
.
Let
![]() $P=\{p_{1},p_{2},\ldots ,p_{n}\}$
. We may assume that the labeling of the elements of
$P=\{p_{1},p_{2},\ldots ,p_{n}\}$
. We may assume that the labeling of the elements of
![]() $P$
is chosen such that
$P$
is chosen such that
![]() $p_{i}<p_{j}$
implies
$p_{i}<p_{j}$
implies
![]() $i<j$
. Similarly,
$i<j$
. Similarly,
![]() $Q=\{q_{1},q_{2},\ldots ,q_{m}\}$
is labeled. Having fixed this labeling we sometimes write
$Q=\{q_{1},q_{2},\ldots ,q_{m}\}$
is labeled. Having fixed this labeling we sometimes write
![]() $y_{(j_{1},j_{2},\ldots ,j_{n})}$
for
$y_{(j_{1},j_{2},\ldots ,j_{n})}$
for
![]() $y_{\unicode[STIX]{x1D711}}$
if
$y_{\unicode[STIX]{x1D711}}$
if
![]() $\unicode[STIX]{x1D711}(p_{i})=q_{j_{i}}$
for
$\unicode[STIX]{x1D711}(p_{i})=q_{j_{i}}$
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
For
![]() $Q=[2]$
the ideal
$Q=[2]$
the ideal
![]() $J_{P,Q}$
is the defining ideal of the Hibi ring associated with the distributive lattice
$J_{P,Q}$
is the defining ideal of the Hibi ring associated with the distributive lattice
![]() $L=\operatorname{Hom}(P,[2])$
. In this case it is known that
$L=\operatorname{Hom}(P,[2])$
. In this case it is known that
![]() $J_{P,Q}$
has a quadratic Gröbner basis, [Reference Herzog and Hibi9, Theorem 10.1.3]. For arbitrary posets
$J_{P,Q}$
has a quadratic Gröbner basis, [Reference Herzog and Hibi9, Theorem 10.1.3]. For arbitrary posets
![]() $P$
and
$P$
and
![]() $Q$
the ideal
$Q$
the ideal
![]() $J_{P,Q}$
is not always generated in degree
$J_{P,Q}$
is not always generated in degree
![]() $2$
. The simplest example is given by the posets
$2$
. The simplest example is given by the posets
![]() $P$
and
$P$
and
![]() $Q$
displayed in Figure 3.
$Q$
displayed in Figure 3.
In this example
![]() $J_{P,Q}$
is generated by the binomial
$J_{P,Q}$
is generated by the binomial
![]() $y_{(1,4)}y_{(2,5)}y_{(3,6)}-y_{(1,5)}y_{(2,6)}y_{(3,4)}$
.
$y_{(1,4)}y_{(2,5)}y_{(3,6)}-y_{(1,5)}y_{(2,6)}y_{(3,4)}$
.
It is known that in general
![]() $J_{P,Q}$
is generated by binomials. Consult [Reference Hibi12] for fundamental materials on toric ideals and Gröbner basis.
$J_{P,Q}$
is generated by binomials. Consult [Reference Hibi12] for fundamental materials on toric ideals and Gröbner basis.
We identify each
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
with the sequence
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
with the sequence
![]() $(j_{1}^{(\unicode[STIX]{x1D711})},\ldots ,j_{n}^{(\unicode[STIX]{x1D711})})$
, where
$(j_{1}^{(\unicode[STIX]{x1D711})},\ldots ,j_{n}^{(\unicode[STIX]{x1D711})})$
, where
![]() $\unicode[STIX]{x1D711}(p_{i})=q_{j_{i}^{(\unicode[STIX]{x1D711})}}$
for
$\unicode[STIX]{x1D711}(p_{i})=q_{j_{i}^{(\unicode[STIX]{x1D711})}}$
for
![]() $1\leqslant i\leqslant n$
. We introduce the total ordering
$1\leqslant i\leqslant n$
. We introduce the total ordering
![]() ${<}$
of the variables
${<}$
of the variables
![]() $y_{\unicode[STIX]{x1D711}}$
with
$y_{\unicode[STIX]{x1D711}}$
with
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
by setting
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
by setting
![]() $y_{\unicode[STIX]{x1D711}}<y_{\unicode[STIX]{x1D713}}$
if
$y_{\unicode[STIX]{x1D711}}<y_{\unicode[STIX]{x1D713}}$
if
![]() $j_{i_{0}}^{(\unicode[STIX]{x1D711})}<j_{i_{0}}^{(\unicode[STIX]{x1D713})}$
, where
$j_{i_{0}}^{(\unicode[STIX]{x1D711})}<j_{i_{0}}^{(\unicode[STIX]{x1D713})}$
, where
![]() $i_{0}$
is the smallest integer for which
$i_{0}$
is the smallest integer for which
![]() $j_{i_{0}}^{(\unicode[STIX]{x1D711})}\neq j_{i_{0}}^{(\unicode[STIX]{x1D713})}$
. Let
$j_{i_{0}}^{(\unicode[STIX]{x1D711})}\neq j_{i_{0}}^{(\unicode[STIX]{x1D713})}$
. Let
![]() ${<}_{\text{rev}}$
denote the reverse lexicographic order on
${<}_{\text{rev}}$
denote the reverse lexicographic order on
![]() $S$
induced by the above ordering
$S$
induced by the above ordering
![]() ${<}$
of the variables
${<}$
of the variables
![]() $y_{\unicode[STIX]{x1D711}}$
with
$y_{\unicode[STIX]{x1D711}}$
with
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
.
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
.
Example 5.1. Let
![]() $P=\{p_{1},p_{2},p_{3}\}$
, where
$P=\{p_{1},p_{2},p_{3}\}$
, where
![]() $p_{1}<p_{2}$
and
$p_{1}<p_{2}$
and
![]() $p_{1}<p_{3}$
, and
$p_{1}<p_{3}$
, and
![]() $Q=\{q_{1},q_{2},q_{3}\}$
, where
$Q=\{q_{1},q_{2},q_{3}\}$
, where
![]() $q_{1}<q_{3}$
and
$q_{1}<q_{3}$
and
![]() $q_{2}<q_{3}$
. Then the total ordering
$q_{2}<q_{3}$
. Then the total ordering
![]() ${<}$
on the variables
${<}$
on the variables
![]() $y_{\unicode[STIX]{x1D711}}$
with
$y_{\unicode[STIX]{x1D711}}$
with
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
is
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
is
We say that
![]() $u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
is nonstandard with respect to
$u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
is nonstandard with respect to
![]() ${<}_{\operatorname{rev}}$
if there exist
${<}_{\operatorname{rev}}$
if there exist
![]() $\unicode[STIX]{x1D711}^{\prime }$
and
$\unicode[STIX]{x1D711}^{\prime }$
and
![]() $\unicode[STIX]{x1D713}^{\prime }$
for which
$\unicode[STIX]{x1D713}^{\prime }$
for which
![]() $u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}=u_{\unicode[STIX]{x1D711}^{\prime }}u_{\unicode[STIX]{x1D713}^{\prime }}$
and
$u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}=u_{\unicode[STIX]{x1D711}^{\prime }}u_{\unicode[STIX]{x1D713}^{\prime }}$
and
![]() $y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
. An expression
$y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
. An expression
![]() $w=u_{\unicode[STIX]{x1D711}_{1}}u_{\unicode[STIX]{x1D711}_{2}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
of a monomial
$w=u_{\unicode[STIX]{x1D711}_{1}}u_{\unicode[STIX]{x1D711}_{2}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
of a monomial
![]() $w$
belonging to
$w$
belonging to
![]() $K[P,Q]$
is called standard if no
$K[P,Q]$
is called standard if no
![]() $u_{\unicode[STIX]{x1D711}_{i}}u_{\unicode[STIX]{x1D711}_{j}}$
, where
$u_{\unicode[STIX]{x1D711}_{i}}u_{\unicode[STIX]{x1D711}_{j}}$
, where
![]() $1\leqslant i<j\leqslant s$
, is nonstandard. It follows that each monomial possesses a standard expression. However, a standard expression of a monomial may not be unique.
$1\leqslant i<j\leqslant s$
, is nonstandard. It follows that each monomial possesses a standard expression. However, a standard expression of a monomial may not be unique.
Example 5.2. Let
![]() $P=[2]$
and
$P=[2]$
and
![]() $Q$
be as in Figure 3. Then each of the expressions
$Q$
be as in Figure 3. Then each of the expressions
![]() $u_{(1,4)}u_{(2,5)}u_{(3,6)}$
and
$u_{(1,4)}u_{(2,5)}u_{(3,6)}$
and
![]() $u_{(1,5)}u_{(2,6)}u_{(3,4)}$
of the monomial
$u_{(1,5)}u_{(2,6)}u_{(3,4)}$
of the monomial
![]() $x_{11}x_{12}x_{13}x_{24}x_{25}x_{26}$
is standard.
$x_{11}x_{12}x_{13}x_{24}x_{25}x_{26}$
is standard.
Lemma 5.3. Let
![]() $P=\{p_{1},\ldots ,p_{n}\}$
be an arbitrary finite poset and
$P=\{p_{1},\ldots ,p_{n}\}$
be an arbitrary finite poset and
![]() $Q=[2]$
. Then every monomial belonging to
$Q=[2]$
. Then every monomial belonging to
![]() $K[P,Q]$
possesses a unique standard expression.
$K[P,Q]$
possesses a unique standard expression.
Proof. Let
![]() $w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
with
$w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
with
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
. Suppose that there exist
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
. Suppose that there exist
![]() $2\leqslant i_{0}\leqslant n$
and
$2\leqslant i_{0}\leqslant n$
and
![]() $1\leqslant k<k^{\prime }\leqslant s$
for which
$1\leqslant k<k^{\prime }\leqslant s$
for which
![]() $\unicode[STIX]{x1D711}_{k}(p_{i_{0}})=2$
and
$\unicode[STIX]{x1D711}_{k}(p_{i_{0}})=2$
and
![]() $\unicode[STIX]{x1D711}_{k^{\prime }}(p_{i_{0}})=1$
. Since
$\unicode[STIX]{x1D711}_{k^{\prime }}(p_{i_{0}})=1$
. Since
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, it follows that there is
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, it follows that there is
![]() $1\leqslant i^{\prime }<i_{0}$
with
$1\leqslant i^{\prime }<i_{0}$
with
![]() $\unicode[STIX]{x1D711}_{k}(p_{i^{\prime }})=1$
and
$\unicode[STIX]{x1D711}_{k}(p_{i^{\prime }})=1$
and
![]() $\unicode[STIX]{x1D711}_{k^{\prime }}(p_{i^{\prime }})=2$
. Since each of the inverse images
$\unicode[STIX]{x1D711}_{k^{\prime }}(p_{i^{\prime }})=2$
. Since each of the inverse images
![]() $\unicode[STIX]{x1D711}_{k}^{-1}(1)$
and
$\unicode[STIX]{x1D711}_{k}^{-1}(1)$
and
![]() $\unicode[STIX]{x1D711}_{k^{\prime }}^{-1}(1)$
is a poset ideal of
$\unicode[STIX]{x1D711}_{k^{\prime }}^{-1}(1)$
is a poset ideal of
![]() $P$
, it follows that each of the maps
$P$
, it follows that each of the maps
![]() $\unicode[STIX]{x1D713}_{k}:P\rightarrow Q$
and
$\unicode[STIX]{x1D713}_{k}:P\rightarrow Q$
and
![]() $\unicode[STIX]{x1D713}_{k^{\prime }}:P\rightarrow Q$
defined by setting
$\unicode[STIX]{x1D713}_{k^{\prime }}:P\rightarrow Q$
defined by setting
for
![]() $1\leqslant i\leqslant n$
is isotone. Furthermore, one has
$1\leqslant i\leqslant n$
is isotone. Furthermore, one has
![]() $y_{\unicode[STIX]{x1D713}_{k}}y_{\unicode[STIX]{x1D713}_{k^{\prime }}}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}_{k}}y_{\unicode[STIX]{x1D711}_{k^{\prime }}}$
and
$y_{\unicode[STIX]{x1D713}_{k}}y_{\unicode[STIX]{x1D713}_{k^{\prime }}}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}_{k}}y_{\unicode[STIX]{x1D711}_{k^{\prime }}}$
and
![]() $u_{\unicode[STIX]{x1D711}_{k}}u_{\unicode[STIX]{x1D711}_{k^{\prime }}}=u_{\unicode[STIX]{x1D713}_{k}}u_{\unicode[STIX]{x1D713}_{k^{\prime }}}$
. Thus
$u_{\unicode[STIX]{x1D711}_{k}}u_{\unicode[STIX]{x1D711}_{k^{\prime }}}=u_{\unicode[STIX]{x1D713}_{k}}u_{\unicode[STIX]{x1D713}_{k^{\prime }}}$
. Thus
![]() $w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
cannot be standard. Since
$w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
cannot be standard. Since
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, it follows that
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, it follows that
Hence, if
![]() $w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
is standard with
$w=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
is standard with
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, then
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
, then
for
![]() $1\leqslant i\leqslant n$
. This guarantees that a standard expression of each monomial belonging to
$1\leqslant i\leqslant n$
. This guarantees that a standard expression of each monomial belonging to
![]() $K[P,Q]$
is unique, as desired.◻
$K[P,Q]$
is unique, as desired.◻
A finite poset
![]() $Q$
is called a rooted tree if whenever
$Q$
is called a rooted tree if whenever
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
belong to
$\unicode[STIX]{x1D6FE}$
belong to
![]() $Q$
with
$Q$
with
![]() $\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FC}$
, then either
$\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FC}$
, then either
![]() $\unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D6FE}$
or
$\unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D6FE}$
or
![]() $\unicode[STIX]{x1D6FE}\leqslant \unicode[STIX]{x1D6FD}$
. In other words, a finite poset
$\unicode[STIX]{x1D6FE}\leqslant \unicode[STIX]{x1D6FD}$
. In other words, a finite poset
![]() $Q$
is a rooted tree if a maximal chain of
$Q$
is a rooted tree if a maximal chain of
![]() $Q$
descending from each
$Q$
descending from each
![]() $\unicode[STIX]{x1D6FC}\in Q$
is unique. A finite poset is a co-rooted tree if its dual poset is a rooted tree.
$\unicode[STIX]{x1D6FC}\in Q$
is unique. A finite poset is a co-rooted tree if its dual poset is a rooted tree.
Lemma 5.4. Let
![]() $P=[2]$
and let
$P=[2]$
and let
![]() $Q$
be a co-rooted tree. Then each monomial belonging to
$Q$
be a co-rooted tree. Then each monomial belonging to
![]() $K[P,Q]$
possesses a unique standard expression.
$K[P,Q]$
possesses a unique standard expression.
Proof. Let
![]() $u$
be a monomial belonging to
$u$
be a monomial belonging to
![]() $K[P,Q]$
. Let
$K[P,Q]$
. Let
![]() $u=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
$u=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $u=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
be standard expressions of
$u=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
be standard expressions of
![]() $u$
with
$u$
with
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
and
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $y_{\unicode[STIX]{x1D713}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D713}_{s}}$
. Then one has
$y_{\unicode[STIX]{x1D713}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D713}_{s}}$
. Then one has
![]() $\unicode[STIX]{x1D711}_{k}(1)=\unicode[STIX]{x1D713}_{k}(1)$
for
$\unicode[STIX]{x1D711}_{k}(1)=\unicode[STIX]{x1D713}_{k}(1)$
for
![]() $1\leqslant k\leqslant s$
. Furthermore,
$1\leqslant k\leqslant s$
. Furthermore,
![]() $\unicode[STIX]{x1D711}_{k}(1)\leqslant \unicode[STIX]{x1D711}_{k}(2)$
and
$\unicode[STIX]{x1D711}_{k}(1)\leqslant \unicode[STIX]{x1D711}_{k}(2)$
and
![]() $\unicode[STIX]{x1D713}_{k}(1)\leqslant \unicode[STIX]{x1D713}_{k}(2)$
for
$\unicode[STIX]{x1D713}_{k}(1)\leqslant \unicode[STIX]{x1D713}_{k}(2)$
for
![]() $1\leqslant k\leqslant s$
. In order to show that the standard expressions
$1\leqslant k\leqslant s$
. In order to show that the standard expressions
![]() $u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
$u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
coincide, we may assume without loss of generality that
$u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
coincide, we may assume without loss of generality that
![]() $\unicode[STIX]{x1D711}_{i}\neq \unicode[STIX]{x1D713}_{j}$
for all
$\unicode[STIX]{x1D711}_{i}\neq \unicode[STIX]{x1D713}_{j}$
for all
![]() $i$
and
$i$
and
![]() $j$
. Since
$j$
. Since
![]() $Q$
is a co-rooted tree and since
$Q$
is a co-rooted tree and since
![]() $\unicode[STIX]{x1D711}_{1}(1)\leqslant \unicode[STIX]{x1D711}_{1}(2)$
and
$\unicode[STIX]{x1D711}_{1}(1)\leqslant \unicode[STIX]{x1D711}_{1}(2)$
and
![]() $\unicode[STIX]{x1D713}_{1}(1)\leqslant \unicode[STIX]{x1D713}_{1}(2)$
with
$\unicode[STIX]{x1D713}_{1}(1)\leqslant \unicode[STIX]{x1D713}_{1}(2)$
with
![]() $\unicode[STIX]{x1D711}_{1}(1)=\unicode[STIX]{x1D713}_{1}(1)$
, it follows that
$\unicode[STIX]{x1D711}_{1}(1)=\unicode[STIX]{x1D713}_{1}(1)$
, it follows that
![]() $\unicode[STIX]{x1D711}_{1}(2)$
and
$\unicode[STIX]{x1D711}_{1}(2)$
and
![]() $\unicode[STIX]{x1D713}_{1}(2)$
are comparable. Let, say,
$\unicode[STIX]{x1D713}_{1}(2)$
are comparable. Let, say,
![]() $\unicode[STIX]{x1D711}_{1}(2)<\unicode[STIX]{x1D713}_{1}(2)$
. Since
$\unicode[STIX]{x1D711}_{1}(2)<\unicode[STIX]{x1D713}_{1}(2)$
. Since
![]() $u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
, there is
$u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
, there is
![]() $2\leqslant k_{0}\leqslant s$
with
$2\leqslant k_{0}\leqslant s$
with
![]() $\unicode[STIX]{x1D713}_{k_{0}}(2)=\unicode[STIX]{x1D711}_{1}(2)$
. Hence
$\unicode[STIX]{x1D713}_{k_{0}}(2)=\unicode[STIX]{x1D711}_{1}(2)$
. Hence
![]() $\unicode[STIX]{x1D713}_{k_{0}}(1)\leqslant \unicode[STIX]{x1D713}_{k_{0}}(2)<\unicode[STIX]{x1D713}_{1}(2)$
and
$\unicode[STIX]{x1D713}_{k_{0}}(1)\leqslant \unicode[STIX]{x1D713}_{k_{0}}(2)<\unicode[STIX]{x1D713}_{1}(2)$
and
![]() $\unicode[STIX]{x1D713}_{1}(1)\leqslant \unicode[STIX]{x1D713}_{k_{0}}(2)<\unicode[STIX]{x1D713}_{1}(2)$
. One can then define
$\unicode[STIX]{x1D713}_{1}(1)\leqslant \unicode[STIX]{x1D713}_{k_{0}}(2)<\unicode[STIX]{x1D713}_{1}(2)$
. One can then define
![]() $\unicode[STIX]{x1D713}_{1}^{\prime }$
and
$\unicode[STIX]{x1D713}_{1}^{\prime }$
and
![]() $\unicode[STIX]{x1D713}_{k_{0}}^{\prime }$
belonging to
$\unicode[STIX]{x1D713}_{k_{0}}^{\prime }$
belonging to
![]() $\operatorname{Hom}(P,Q)$
by setting
$\operatorname{Hom}(P,Q)$
by setting
Then
![]() $u_{\unicode[STIX]{x1D713}_{1}}u_{\unicode[STIX]{x1D713}_{k_{0}}}=u_{\unicode[STIX]{x1D713}_{1}^{\prime }}u_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}$
with
$u_{\unicode[STIX]{x1D713}_{1}}u_{\unicode[STIX]{x1D713}_{k_{0}}}=u_{\unicode[STIX]{x1D713}_{1}^{\prime }}u_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}$
with
![]() $y_{\unicode[STIX]{x1D713}_{1}^{\prime }}<y_{\unicode[STIX]{x1D713}_{1}}\leqslant y_{\unicode[STIX]{x1D713}_{k_{0}}}$
. Furthermore,
$y_{\unicode[STIX]{x1D713}_{1}^{\prime }}<y_{\unicode[STIX]{x1D713}_{1}}\leqslant y_{\unicode[STIX]{x1D713}_{k_{0}}}$
. Furthermore,
![]() $y_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}\geqslant y_{\unicode[STIX]{x1D713}_{1}^{\prime }}$
. Hence
$y_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}\geqslant y_{\unicode[STIX]{x1D713}_{1}^{\prime }}$
. Hence
![]() $y_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}y_{\unicode[STIX]{x1D713}_{1}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D713}_{k_{0}}}y_{\unicode[STIX]{x1D713}_{1}}$
. It then follows that
$y_{\unicode[STIX]{x1D713}_{k_{0}}^{\prime }}y_{\unicode[STIX]{x1D713}_{1}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D713}_{k_{0}}}y_{\unicode[STIX]{x1D713}_{1}}$
. It then follows that
![]() $u_{\unicode[STIX]{x1D713}_{1}}u_{\unicode[STIX]{x1D713}_{k_{0}}}$
cannot be standard. Hence a standard expression of each monomial belonging to
$u_{\unicode[STIX]{x1D713}_{1}}u_{\unicode[STIX]{x1D713}_{k_{0}}}$
cannot be standard. Hence a standard expression of each monomial belonging to
![]() $K[P,Q]$
is unique, as desired.◻
$K[P,Q]$
is unique, as desired.◻
Theorem 5.5. Let
![]() $P$
be a chain and
$P$
be a chain and
![]() $Q$
a co-rooted tree. Then each monomial belonging to
$Q$
a co-rooted tree. Then each monomial belonging to
![]() $K[P,Q]$
possesses a unique standard expression.
$K[P,Q]$
possesses a unique standard expression.
Proof. We may assume that
![]() $P=[n]$
. Then for each
$P=[n]$
. Then for each
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
, one has
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
, one has
![]() $q_{j_{1}^{(\unicode[STIX]{x1D711})}}\leqslant \cdots \leqslant q_{j_{n}^{(\unicode[STIX]{x1D711})}}$
. In other words, the image
$q_{j_{1}^{(\unicode[STIX]{x1D711})}}\leqslant \cdots \leqslant q_{j_{n}^{(\unicode[STIX]{x1D711})}}$
. In other words, the image
![]() $\unicode[STIX]{x1D711}([n])$
is a multichain (chain with repetitions) of
$\unicode[STIX]{x1D711}([n])$
is a multichain (chain with repetitions) of
![]() $Q$
of length
$Q$
of length
![]() $n$
. It then follows that
$n$
. It then follows that
![]() $u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
with
$u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
with
![]() $y_{\unicode[STIX]{x1D711}}<y_{\unicode[STIX]{x1D713}}$
is nonstandard if and only if there is
$y_{\unicode[STIX]{x1D711}}<y_{\unicode[STIX]{x1D713}}$
is nonstandard if and only if there is
![]() $2\leqslant i\leqslant n$
with
$2\leqslant i\leqslant n$
with
![]() $\unicode[STIX]{x1D711}(i)>\unicode[STIX]{x1D713}(i)$
such that
$\unicode[STIX]{x1D711}(i)>\unicode[STIX]{x1D713}(i)$
such that
![]() $\unicode[STIX]{x1D711}(i-1)\leqslant \unicode[STIX]{x1D713}(i)$
and
$\unicode[STIX]{x1D711}(i-1)\leqslant \unicode[STIX]{x1D713}(i)$
and
![]() $\unicode[STIX]{x1D713}(i-1)\leqslant \unicode[STIX]{x1D711}(i)$
. In fact, one has
$\unicode[STIX]{x1D713}(i-1)\leqslant \unicode[STIX]{x1D711}(i)$
. In fact, one has
![]() $y_{\unicode[STIX]{x1D713}^{\prime }}y_{\unicode[STIX]{x1D711}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D713}}y_{\unicode[STIX]{x1D711}}$
, where
$y_{\unicode[STIX]{x1D713}^{\prime }}y_{\unicode[STIX]{x1D711}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D713}}y_{\unicode[STIX]{x1D711}}$
, where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{\prime } & = & \displaystyle (j_{\unicode[STIX]{x1D711}}^{(1)},\ldots ,j_{\unicode[STIX]{x1D711}}^{(i-1)},j_{\unicode[STIX]{x1D713}}^{(i)},\ldots ,j_{\unicode[STIX]{x1D713}}^{(n)})\quad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D713}^{\prime } & = & \displaystyle (j_{\unicode[STIX]{x1D713}}^{(1)},\ldots ,j_{\unicode[STIX]{x1D713}}^{(i-1)},j_{\unicode[STIX]{x1D711}}^{(i)},\ldots ,j_{\unicode[STIX]{x1D711}}^{(n)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{\prime } & = & \displaystyle (j_{\unicode[STIX]{x1D711}}^{(1)},\ldots ,j_{\unicode[STIX]{x1D711}}^{(i-1)},j_{\unicode[STIX]{x1D713}}^{(i)},\ldots ,j_{\unicode[STIX]{x1D713}}^{(n)})\quad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D713}^{\prime } & = & \displaystyle (j_{\unicode[STIX]{x1D713}}^{(1)},\ldots ,j_{\unicode[STIX]{x1D713}}^{(i-1)},j_{\unicode[STIX]{x1D711}}^{(i)},\ldots ,j_{\unicode[STIX]{x1D711}}^{(n)}).\nonumber\end{eqnarray}$$
Given
![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
, we introduce
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(P,Q)$
, we introduce
![]() $\unicode[STIX]{x1D711}^{\ast }\in \operatorname{Hom}(P\setminus \{n\},Q)$
by setting
$\unicode[STIX]{x1D711}^{\ast }\in \operatorname{Hom}(P\setminus \{n\},Q)$
by setting
![]() $\unicode[STIX]{x1D711}^{\ast }(i)=\unicode[STIX]{x1D711}(i)$
for
$\unicode[STIX]{x1D711}^{\ast }(i)=\unicode[STIX]{x1D711}(i)$
for
![]() $i\in [n-1]$
. Let
$i\in [n-1]$
. Let
![]() $u$
be a monomial belonging to
$u$
be a monomial belonging to
![]() $K[P,Q]$
. Let
$K[P,Q]$
. Let
![]() $u=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
$u=u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $u=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
be standard expressions of
$u=u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
be standard expressions of
![]() $u$
with
$u$
with
![]() $y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
and
$y_{\unicode[STIX]{x1D711}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $y_{\unicode[STIX]{x1D713}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D713}_{s}}$
. The above observation guarantees that each of
$y_{\unicode[STIX]{x1D713}_{1}}\leqslant \cdots \leqslant y_{\unicode[STIX]{x1D713}_{s}}$
. The above observation guarantees that each of
![]() $u_{\unicode[STIX]{x1D711}_{1}^{\ast }}\cdots u_{\unicode[STIX]{x1D711}_{s}^{\ast }}$
and
$u_{\unicode[STIX]{x1D711}_{1}^{\ast }}\cdots u_{\unicode[STIX]{x1D711}_{s}^{\ast }}$
and
![]() $u_{\unicode[STIX]{x1D713}_{1}^{\ast }}\cdots u_{\unicode[STIX]{x1D713}_{s}^{\ast }}$
is a standard expression. Thus, working on induction on
$u_{\unicode[STIX]{x1D713}_{1}^{\ast }}\cdots u_{\unicode[STIX]{x1D713}_{s}^{\ast }}$
is a standard expression. Thus, working on induction on
![]() $n$
, it follows that
$n$
, it follows that
![]() $\unicode[STIX]{x1D711}_{k}^{\ast }=\unicode[STIX]{x1D713}_{k}^{\ast }$
for
$\unicode[STIX]{x1D711}_{k}^{\ast }=\unicode[STIX]{x1D713}_{k}^{\ast }$
for
![]() $1\leqslant k\leqslant s$
. In particular
$1\leqslant k\leqslant s$
. In particular
![]() $\unicode[STIX]{x1D711}_{k}(n-1)=\unicode[STIX]{x1D713}_{k}(n-1)$
for
$\unicode[STIX]{x1D711}_{k}(n-1)=\unicode[STIX]{x1D713}_{k}(n-1)$
for
![]() $1\leqslant k\leqslant s$
.
$1\leqslant k\leqslant s$
.
Now, in order to show that the standard expressions
![]() $u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
$u_{\unicode[STIX]{x1D711}_{1}}\cdots u_{\unicode[STIX]{x1D711}_{s}}$
and
![]() $u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
coincide, one must show that
$u_{\unicode[STIX]{x1D713}_{1}}\cdots u_{\unicode[STIX]{x1D713}_{s}}$
coincide, one must show that
![]() $\unicode[STIX]{x1D711}_{k}(n)=\unicode[STIX]{x1D713}_{k}(n)$
for
$\unicode[STIX]{x1D711}_{k}(n)=\unicode[STIX]{x1D713}_{k}(n)$
for
![]() $1\leqslant k\leqslant s$
. This can be done by using the same technique as in the proof of Lemma 5.4.◻
$1\leqslant k\leqslant s$
. This can be done by using the same technique as in the proof of Lemma 5.4.◻
Corollary 5.6. Let
![]() $P$
be a chain and suppose that each connected component of
$P$
be a chain and suppose that each connected component of
![]() $Q$
is either a rooted or a co-rooted poset. Then the toric ideal
$Q$
is either a rooted or a co-rooted poset. Then the toric ideal
![]() $J_{P,Q}$
possesses a quadratic Gröbner basis.
$J_{P,Q}$
possesses a quadratic Gröbner basis.
Proof. Let
![]() $Q$
be a co-rooted tree. Let
$Q$
be a co-rooted tree. Let
![]() ${\mathcal{G}}$
denote the set of quadratic binomials of
${\mathcal{G}}$
denote the set of quadratic binomials of
![]() $S$
of the form
$S$
of the form
![]() $y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}-y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}$
with
$y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}-y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}$
with
![]() $y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
. Furthermore, write
$y_{\unicode[STIX]{x1D711}^{\prime }}y_{\unicode[STIX]{x1D713}^{\prime }}{<}_{\operatorname{rev}}y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
. Furthermore, write
![]() $\text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
for the monomial ideal of
$\text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
for the monomial ideal of
![]() $S$
which is generated by those quadratic monomials
$S$
which is generated by those quadratic monomials
![]() $y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
for which
$y_{\unicode[STIX]{x1D711}}y_{\unicode[STIX]{x1D713}}$
for which
![]() $u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
are nonstandard. Let
$u_{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D713}}$
are nonstandard. Let
![]() $w$
and
$w$
and
![]() $w^{\prime }$
be monomials of
$w^{\prime }$
be monomials of
![]() $S$
with
$S$
with
![]() $w\neq w^{\prime }$
such that neither
$w\neq w^{\prime }$
such that neither
![]() $w$
nor
$w$
nor
![]() $w^{\prime }$
belongs to
$w^{\prime }$
belongs to
![]() $\text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
. It then follows from Theorem 5.5 that
$\text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
. It then follows from Theorem 5.5 that
![]() $\unicode[STIX]{x1D70B}(w)\neq \unicode[STIX]{x1D70B}(w^{\prime })$
. In other words, the set of those monomials
$\unicode[STIX]{x1D70B}(w)\neq \unicode[STIX]{x1D70B}(w^{\prime })$
. In other words, the set of those monomials
![]() $\unicode[STIX]{x1D70B}(w)$
of
$\unicode[STIX]{x1D70B}(w)$
of
![]() $K[P,Q]$
with
$K[P,Q]$
with
![]() $w\not \in \text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
is linearly independent. By virtue of the well-known technique ([Reference Aramova, Herzog and Hibi1, Lemma 1.1] and [Reference Ohsugi and Hibi16, (0.1)]) on initial ideals, this fact guarantees that
$w\not \in \text{in}_{{<}_{\operatorname{rev}}}({\mathcal{G}})$
is linearly independent. By virtue of the well-known technique ([Reference Aramova, Herzog and Hibi1, Lemma 1.1] and [Reference Ohsugi and Hibi16, (0.1)]) on initial ideals, this fact guarantees that
![]() ${\mathcal{G}}$
is a quadratic Gröbner basis of
${\mathcal{G}}$
is a quadratic Gröbner basis of
![]() $J_{P,Q}$
with respect to
$J_{P,Q}$
with respect to
![]() ${<}_{\operatorname{rev}}$
, as desired.
${<}_{\operatorname{rev}}$
, as desired.
Let
![]() $Q$
be a rooted tree. Lemma 2.5 says that
$Q$
be a rooted tree. Lemma 2.5 says that
![]() $K[P^{\vee },Q^{\vee }]$
is isomorphic to
$K[P^{\vee },Q^{\vee }]$
is isomorphic to
![]() $K[P,Q]$
. Since
$K[P,Q]$
. Since
![]() $P^{\vee }=P$
and since
$P^{\vee }=P$
and since
![]() $Q^{\vee }$
is a co-rooted tree, it follows that
$Q^{\vee }$
is a co-rooted tree, it follows that
![]() $J_{P,Q}$
possesses a quadratic Gröbner basis, as required.
$J_{P,Q}$
possesses a quadratic Gröbner basis, as required.
Now assume that each component
![]() $Q_{i}$
$Q_{i}$
![]() $(i=1,\ldots ,m)$
of
$(i=1,\ldots ,m)$
of
![]() $Q$
is either rooted or co-rooted. As seen before, the toric ideal of each
$Q$
is either rooted or co-rooted. As seen before, the toric ideal of each
![]() $K[P,Q_{i}]$
has a quadratic Gröbner basis. Since by Lemma 2.3(b),
$K[P,Q_{i}]$
has a quadratic Gröbner basis. Since by Lemma 2.3(b),
![]() $K[P,Q]$
is the tensor product of the
$K[P,Q]$
is the tensor product of the
![]() $K$
-algebras
$K$
-algebras
![]() $K[P,Q_{i}]$
it follows that the Gröbner basis of
$K[P,Q_{i}]$
it follows that the Gröbner basis of
![]() $J_{P,Q}$
is the union of the Gröbner basis of the
$J_{P,Q}$
is the union of the Gröbner basis of the
![]() $J_{P,Q_{i}}$
. Thus the desired result follows.◻
$J_{P,Q_{i}}$
. Thus the desired result follows.◻
As we have seen at the beginning of this section,
![]() $J_{P,Q}$
is not always generated by quadratic binomials. We say that
$J_{P,Q}$
is not always generated by quadratic binomials. We say that
![]() $C$
is a poset
$C$
is a poset
![]() $\ell$
-cycle, if the vertices of
$\ell$
-cycle, if the vertices of
![]() $C$
are
$C$
are
![]() $a_{1},\ldots ,a_{\ell },b_{1},\ldots ,b_{\ell }$
whose covering relations are
$a_{1},\ldots ,a_{\ell },b_{1},\ldots ,b_{\ell }$
whose covering relations are
![]() $a_{i}<b_{i}$
,
$a_{i}<b_{i}$
,
![]() $a_{i}<b_{i+1}$
for
$a_{i}<b_{i+1}$
for
![]() $1\leqslant i\leqslant \ell$
where
$1\leqslant i\leqslant \ell$
where
![]() $b_{\ell +1}=b_{1}$
. The poset
$b_{\ell +1}=b_{1}$
. The poset
![]() $Q$
in Figure 3 is a poset
$Q$
in Figure 3 is a poset
![]() $6$
-cycle. Note that not any cycle of
$6$
-cycle. Note that not any cycle of
![]() $G(P)$
is a poset cycle (see for example Figure 4).
$G(P)$
is a poset cycle (see for example Figure 4).
Figure 4. A cycle but not a poset cycle.
Based on Theorem 5.5, Corollary 5.6 and experimental evidence we propose
Conjecture 5.7. Let
![]() $P,Q\in {\mathcal{P}}$
, and assume that
$P,Q\in {\mathcal{P}}$
, and assume that
![]() $Q$
does not contain any induced poset cycle of length greater than 4. Then
$Q$
does not contain any induced poset cycle of length greater than 4. Then
![]() $J_{P,Q}$
is generated by quadratic binomials.
$J_{P,Q}$
is generated by quadratic binomials.
The poset
![]() $Q$
given in Figure 3 is a poset cycle. As expected by our conjecture,
$Q$
given in Figure 3 is a poset cycle. As expected by our conjecture,
![]() $J_{[2],Q}$
is not generated by quadrics. Actually,
$J_{[2],Q}$
is not generated by quadrics. Actually,
![]() $J_{[2],Q}$
does not even possess a quadratic Gröbner basis with respect to the reverse lexicographic term order induced by the natural order of the variables.
$J_{[2],Q}$
does not even possess a quadratic Gröbner basis with respect to the reverse lexicographic term order induced by the natural order of the variables.