Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T03:46:05.799Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICATION FORMULAS AND SEMISIMPLICITY FOR 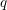$q$-SCHUR SUPERALGEBRAS

Part of: General nonassociative rings Linear algebraic groups and related topics Permutation groups Representation theory of groups

Published online by Cambridge University Press:  30 April 2018

JIE DU ,
HAIXIA GU  and
ZHONGGUO ZHOU
JIE DU
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia email j.du@unsw.edu.au
HAIXIA GU*
Affiliation:
School of Science, Huzhou University, Huzhou 313000, China email ghx@zjhu.edu.cn
ZHONGGUO ZHOU
Affiliation:
College of Science, Hohai University, Nanjing 210098, China email zhgzhou@hhu.edu.cn
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate products of certain double cosets for the symmetric group and use the findings to derive some multiplication formulas for the 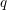$q$-Schur superalgebras. This gives a combinatorialization of the relative norm approach developed in Du and Gu (A realization of the quantum supergroup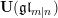$\mathbf{U}(\mathfrak{g}\mathfrak{l}_{m|n})$, J. Algebra 404 (2014), 60–99). We then give several applications of the multiplication formulas, including the matrix representation of the regular representation and a semisimplicity criterion for 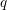$q$-Schur superalgebras. We also construct infinitesimal and little 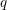$q$-Schur superalgebras directly from the multiplication formulas and develop their semisimplicity criteria.

MSC classification

Primary: 20B30: Symmetric groups 20G43: Schur and $q$-Schur algebras 17A70: Superalgebras 20C08: Hecke algebras and their representations
Type
Article
Information
Nagoya Mathematical Journal , Volume 237 , March 2020 , pp. 98 - 126
Copyright
© 2018 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work was supported by a 2017 UNSW Science Goldstar Grant and the Natural Science Foundation of China (#11501197, #11671234). The third author would like to thank UNSW for its hospitality during his a year visit and thank the Jiangsu Provincial Department of Education for financial support.

References

Beilinson, A. A., Lusztig, G. and MacPherson, R., A geometric setting for the quantum deformation of GL n , Duke Math. J. 61 (1990), 655–677.Google Scholar
Bao, H., Kujawa, J., Li, Y. and Wang, W., Geometric Schur duality of classical type , Transf. Groups, to appear.Google Scholar
Chen, X., Gu, H. and Wang, J., Infinitesimal and little q-Schur superalgebras , Comm. Algebra, to appear.Google Scholar
Deng, B., Du, J. and Fu, Q., A Double Hall Algebra Approach to Affine Quantum Schur–Weyl Theory, LMS Lecture Note Series 401 , Cambridge University Press, 2012.Google Scholar
Deng, B., Du, J., Parshall, B. and Wang, J. P., Finite Dimensional Alegebras and Quantum Groups, Mathematical Surveys and Monographs 150 , American Mathematical Society, Providence, RI, 2008.Google Scholar
Doty, S. and Nakano, D., Semisimple Schur algebras , Math. Proc. Cambridge Philos. Soc. 124 (1998), 15–20.Google Scholar
Doty, S., Nakano, D. and Peters, K., Infinitesimal Schur algebras , Proc. Lond. Math. Soc. 72 (1996), 588–612.Google Scholar
Du, J., The modular representation theory of q-Schur algebras , Trans. Amer. Math. Soc. 329 (1992), 253–271.Google Scholar
Du, J. and Fu, Q., Quantum affine gln via Hecke algebras , Adv. Math. 282 (2015), 23–46.Google Scholar
Du, J., Fu, Q. and Wang, J., Infinitesimal quantum gln and little q-Schur algebras , J. Algebra 287 (2005), 199–233.Google Scholar
Du, J., Fu, Q. and Wang, J., Representations of little q-Schur algebras , Pacific J. Math. 257 (2012), 343–378.Google Scholar
Du, J. and Gu, H., A realization of the quantum supergroup U(glm|n) , J. Algebra 404 (2014), 60–99.Google Scholar
Du, J. and Gu, H., Canonical bases for the quantum supergroup U(glm|n) , Math. Z. 281 (2015), 631–660.Google Scholar
Du, J., Gu, H. and Wang, J., Irreducible representations of q-Schur superalgebra at a root of unity , J. Pure Appl. Algebra 218 (2014), 2012–2059.Google Scholar
Du, J., Gu, H. and Wang, J., Representations of q-Schur superalgebras in positive characteristics , J. Algebra 481 (2017), 393–419.Google Scholar
Du, J. and Rui, H., Quantum Schur superalgebras and Kazhdan–Lusztig combinatorics , J. Pure Appl. Algebra 215 (2011), 2715–2737.Google Scholar
El Turkey, H. and Kujawa, J., Presenting Schur superalgebras , Pacific J. Math. 262 (2013), 285–316.Google Scholar
Erdmann, K. and Nakano, D. K., Representaiton type of q-Schur algebras , Trans. Amer. Math. Soc. 353 (2001), 4729–4756.Google Scholar
Fan, Z., Lai, C., Li, Y., Luo, L. and Wang, W., Affine flag varieties and quantum symmetric pairs , Mem. Amer. Math. Soc., to appear.Google Scholar
Fan, Z. and Li, Y., Geometric Schur duality of classical type, II , Trans. Amer. Math. Soc., Ser. B 2 (2015), 51–92.Google Scholar
Fu, Q., Semisimple infinitesimal q-Schur algebras , Arch. Math. 90 (2008), 295–303.Google Scholar
Green, J. A., Polynomial Representations of GL n , Second edition, Lecture Notes in Mathematics 830 , Springer, Berlin, 2007, with an appendix on Schensted correspondence and Littelmann paths by K. Erdmann, J. Green and M. Schocker.Google Scholar
Hemmer, D. J., Kujawa, J. and Nakano, D., Representation type of Schur algebras , J. Group Theory 9 (2006), 283–306.Google Scholar
Jones, L., Centers of generic Hecke algebras , Trans. Amer. Math. Soc. 317 (1990), 361–392.Google Scholar
Marko, F. and Zubkov, A. N., Schur superalgebras in characteristic p , Algebr. Represent. Theory 9 (2006), 1–12.Google Scholar
Marko, F. and Zubkov, A. N., Schur superalgebras in characteristic p, II , Bull. Lond. Math. Soc. 38 (2006), 99–112.Google Scholar