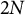1 Introduction
Following the 2020 Census, every state in the United States redrew their congressional and state legislative district boundaries (Warshaw, McGhee, and Migurski Reference Warshaw, McGhee and Migurski2022). Many city councils, school boards, county commissions, and other representative bodies also drew new maps. Redistricting creates opportunities for political actors to benefit certain groups over others. In particular, partisan gerrymandering is used to advantage one political party, even enabling a party to win a majority of the seats in a legislative chamber without winning a majority of votes in the election. For example, in 2018, Republican candidates for the Wisconsin State Assembly won only 45% of the statewide vote but, due to partisan gerrymandering, won 63 of the 99 seats (64%).
Gerrymandering hinders democratic representation in several ways. First, when districts are drawn to amplify disproportionately some voices over others, public policy is less likely to reflect constituent preferences. Second, the public in a representative democracy expects “continued responsiveness of the government to the preferences of its citizens” (Dahl Reference Dahl1971), a relationship fostered by electoral competition and the threat of removing from office lawmakers out of step with their constituents (Canes-Wrone, Brady, and Cogan Reference Canes-Wrone, Brady and Cogan2002). Gerrymandering becomes a critical problem when parties undermine electoral competition by drawing districts that create, enhance, or lock in a partisan advantage and shield representatives from accountability.
Current reforms for partisan gerrymandering, including bipartisan or non-partisan commissions, require either bipartisan cooperation or a neutral third-party actor trusted by both political parties, such as a judge, special master, or independent arbiter, to select a fair map. However, in today’s hyper-partisan environment, there are few such actors considered able to fulfill this role fairly by both sides, and attempts at cooperation have generated acrimony. Intense controversies continue to surround redistricting, even in states that have enacted anti-gerrymandering reforms.
We propose a new method for drawing maps, the Define–Combine Procedure (DCP), which reduces partisan gerrymandering without a neutral third party or bipartisan cooperation. We develop a framework that allows each party to act in their own partisan self-interest but achieves a significantly fairer map than would be drawn by either party on its own. We divide the districting process into two stages. Suppose a state must be divided into N equal-population districts. One party—the “definer”—draws
![]() $2N$
contiguous, equal-population districts. Then, the second party—the “combiner”—selects contiguous pairs of districts from the set defined by the first party to create the final districts. This method produces N equally populated, contiguous districts. By dividing the responsibility of drawing districts into two separate stages, in which each party retains complete autonomy in their own stage, the parties counteract each other’s partisan ambitions while maintaining considerable flexibility to achieve other objectives, including maintaining compactness and communities of interest. Using simulations based on real-world geographic and electoral data, we assess DCP’s performance in all states where congressional redistricting occurs, and we find that DCP produces maps with large reductions in partisan bias, as well as improvements according to several other commonly used redistricting metrics. Compared to adopted plans from the most recent redistricting cycle, our simulations suggest that DCP would likely perform dramatically better than maps originating from state legislatures and politician commissions and at least as well as maps produced by independent commissions and special masters.
$2N$
contiguous, equal-population districts. Then, the second party—the “combiner”—selects contiguous pairs of districts from the set defined by the first party to create the final districts. This method produces N equally populated, contiguous districts. By dividing the responsibility of drawing districts into two separate stages, in which each party retains complete autonomy in their own stage, the parties counteract each other’s partisan ambitions while maintaining considerable flexibility to achieve other objectives, including maintaining compactness and communities of interest. Using simulations based on real-world geographic and electoral data, we assess DCP’s performance in all states where congressional redistricting occurs, and we find that DCP produces maps with large reductions in partisan bias, as well as improvements according to several other commonly used redistricting metrics. Compared to adopted plans from the most recent redistricting cycle, our simulations suggest that DCP would likely perform dramatically better than maps originating from state legislatures and politician commissions and at least as well as maps produced by independent commissions and special masters.
To the best of our knowledge, this represents the first effort to date demonstrating through simulations how a new map-drawing procedure could lead to tangible improvements across such a wide variety of geographic and electoral contexts.
2 Limitations of Current Partisan Gerrymandering Fixes
Reformers have sought to reduce partisan gerrymandering by shifting redistricting authority from partisan legislatures to nonpartisan independent redistricting commissions. State legislatures draw districts in over half of the U.S. states, with the remainder relying on commissions (see Table A.1 in the Supplementary Material). Independent commissions should insulate the redistricting process from the most extreme maps sought by partisans; however, political scientists have not yet reached a full consensus on the success of independent commissions. On the one hand, some recent research has found that independent commissions in the 2020 redistricting cycle tended to produce maps with less partisan bias (Best et al. Reference Best, Lem, Magleby and McDonald2022; Kenny et al. Reference Kenny, McCartan, Simko, Kuriwaki and Imai2023; Warshaw et al. Reference Warshaw, McGhee and Migurski2022); on the other hand, other work has argued that the effectiveness of commissions can be undermined by partisan members of a commission and by tiebreaking procedures that typically benefit one party over the other, reducing incentives for bipartisan mapmaking (Brennan Center for Justice 2018; McDonald Reference McDonald2004; Miller and Grofman Reference Miller and Grofman2013).
In line with this mixed account, the 2020 cycle revealed some notable successes along with some important challenges in states with independent redistricting commissions. In Colorado, independent commissions comprised partially of qualified, randomly selected citizens constructed maps that registered minimal biases.Footnote 1 Maps produced by Michigan’s independent commission registered similarly low levels of bias.Footnote 2 Media accounts of the redistricting cycle have referred to these states’ commissions, independent from legislative interference, as bright spots for selecting fair maps (Wines Reference Wines2022).
The promise of commissions ran up against partisan realities in several other states. In New York, the independent commission failed to produce maps, and the state legislature passed a map that the state’s Supreme Court later determined was a partisan gerrymander. A popular initiative passed in 2018 in Utah establishing an independent commission was altered by Republican state legislators in 2020, allowing them to bypass the commission’s proposed districts. In Virginia, the independent commission had an equal number of Democratic and Republican members and failed to agree upon a map.
While commission-based redistricting appears promising, several structural challenges remain. For one, a majority of commission-based states are not fully independent from interference by a state legislature. Second, and more importantly, states without an initiative process appear unlikely to implement commission-based redistricting. Appendix A.1 of the Supplementary Material further details challenges presented by redistricting in legislatures, commissions, and through litigation.
Academic researchers have drawn inspiration from the cake-cutting problem to propose processes for fairer redistricting. While this logic has inspired several redistricting proposals (Alexeev and Mixon Reference Alexeev and Mixon2019; Benadè, Procaccia, and Tucker-Foltz Reference Benadè, Procaccia and Tucker-Foltz2023; Brams Reference Brams2020; Ely Reference Ely2019; Landau, Reid, and Yershov Reference Landau, Reid and Yershov2009; Pegden, Procaccia, and Yu Reference Pegden, Procaccia and Yu2017), none has addressed implementation across the full range of U.S. states and electoral contexts using real-world data. The complexity of previous proposals also precludes real-world applications or even simulation using modern computing techniques.
DCP contrasts with existing proposals in several ways. First, it does not require either forging bipartisan support between parties or appointing a third-party arbiter to resolve points of difference. A procedure sidestepping these common stumbling blocks could reduce the political disputes that accompany decennial redistricting. Second, DCP is a process-based solution; it does not require courts to define an empirical standard for partisan gerrymandering. State courts could resolve redistricting disputes by ordering parties to use DCP to draw remedial maps, without adjudicating between various measures of bias. Third, DCP is simple and could be implemented efficiently. Several other proposed solutions have appealing game-theoretic properties but in practice require multiple rounds of bargaining and cannot be solved computationally; in contrast, DCP’s two-stage process produces valid districting plans and can be simulated using existing software and processing power, allowing map makers to use it even on short deadlines. Furthermore, state legislatures could implement DCP to guide negotiations, or independent commissions could use DCP as a starting point for a proposal. Process-based solutions that do not require ceding full control of map drawing may be more likely to appeal to partisans within the legislature and represent a pathway toward reform.
3 The Define–Combine Procedure
Suppose a state needs to be divided into N contiguous, equally populated, single-member districts. Elections in the state are contested by two parties: A and B. We assume for simplicity that all people in the state vote in all elections, and their voting decision is based on personal partisan preference.
Let P be the total number of voters in a state, let
![]() $v_A$
be the number of votes in the state for Party A, and let
$v_A$
be the number of votes in the state for Party A, and let
![]() $v_B=P-v_A$
be the number of votes for Party B. For each district d, let
$v_B=P-v_A$
be the number of votes for Party B. For each district d, let
![]() $v_{dA}$
and
$v_{dA}$
and
![]() $v_{dB}$
be the number of votes in the district for each party. A districting map M is a set of N districts, and each district is itself a set of
$v_{dB}$
be the number of votes in the district for each party. A districting map M is a set of N districts, and each district is itself a set of
![]() specific voters. Let
specific voters. Let
![]() $\tau _A$
be the percentage of the statewide votes received by party A,
$\tau _A$
be the percentage of the statewide votes received by party A,
 $$ \begin{align*} \tau_A=\frac{\sum_d^N \nu_{dA}}{\sum_d^N \nu_{dA} + \sum_d^N \nu_{dB}} \end{align*} $$
$$ \begin{align*} \tau_A=\frac{\sum_d^N \nu_{dA}}{\sum_d^N \nu_{dA} + \sum_d^N \nu_{dB}} \end{align*} $$
and
![]() $\tau _B=1-\tau _A$
. For any map, both parties can foresee the number of votes they will receive in each district and the number of districts that they will win.
$\tau _B=1-\tau _A$
. For any map, both parties can foresee the number of votes they will receive in each district and the number of districts that they will win.
We assume that both parties are seat-maximizers; their goal is to win as many of the N seats as possible in the next election. For any given map M, the utility of Party A is
where

and the utility of Party B is
![]() $U_B(M)=1-U_A(M)$
. Both parties are risk-neutral; they are indifferent between winning one district and tying in two districts (with a 50% chance of winning the election in each).
$U_B(M)=1-U_A(M)$
. Both parties are risk-neutral; they are indifferent between winning one district and tying in two districts (with a 50% chance of winning the election in each).
![]() $U_i$
is equivalent to the percentage of seats won by party i.Footnote
3
$U_i$
is equivalent to the percentage of seats won by party i.Footnote
3
3.1 The Unilateral Redistricting Process
We consider two methods of drawing district maps. First, one party has unilateral control of the process. Given a set of potential valid maps
![]() $\mathcal {M}$
, when party i draws the maps, it will select a map
$\mathcal {M}$
, when party i draws the maps, it will select a map
![]() $\widetilde {M_i}\in \mathcal {M}$
that maximizes
$\widetilde {M_i}\in \mathcal {M}$
that maximizes
![]() $U_i$
.Footnote
4
Under this method of redistricting, party i will maximize partisan advantage relative to party j by strategically cracking and packing party j’s voters to minimize the seats won by party j. In many cases, party i will win a substantially larger share of the seats than its statewide vote share, sometimes even translating a minority of statewide votes into a majority of legislative seats.
$U_i$
.Footnote
4
Under this method of redistricting, party i will maximize partisan advantage relative to party j by strategically cracking and packing party j’s voters to minimize the seats won by party j. In many cases, party i will win a substantially larger share of the seats than its statewide vote share, sometimes even translating a minority of statewide votes into a majority of legislative seats.
This method, which we call the “unilateral redistricting process” (URP), approximates the redistricting process in states where one party controls redistricting. While other factors, such as incumbency or vote margins in close seats, factor into districting decisions, gerrymandering for partisan gain is a primary objective for the party in power. When independent experts have used map-drawing software to simulate thousands of possible maps in a state, the observed maps in states with unilateral redistricting appear to be among the most partisan possible.Footnote 5
3.2 The Define–Combine Procedure
The second method we consider is our own innovation, the two-stage DCP. In this model, the power to draw the map is divided between the two parties, but in each stage of the process, one party acts unilaterally.
Suppose Party A acts in the first stage as the “Definer,” and Party B acts in the second stage as the “Combiner.” The game proceeds as follows:
-
1. Party A defines a set of
 $2N$
contiguous, equally populated districts. To avoid confusion with the following stage, we refer to these districts as subdistricts.
$2N$
contiguous, equally populated districts. To avoid confusion with the following stage, we refer to these districts as subdistricts. -
2. Party B creates the final map of N districts by combining pairs of contiguous subdistricts.
Party A moves first and has a strategy profile consisting of a selection of a map
![]() $M_A \in \mathcal {M}$
, the set of all maps with
$M_A \in \mathcal {M}$
, the set of all maps with
![]() $2N$
valid districts.Footnote
6
Party B combines subdistricts to create a map
$2N$
valid districts.Footnote
6
Party B combines subdistricts to create a map
![]() $M_B \in Q(M_A)$
, where
$M_B \in Q(M_A)$
, where
![]() $Q(M_A)$
is the set of valid groupings of the subdistricts in
$Q(M_A)$
is the set of valid groupings of the subdistricts in
![]() $M_A$
.
$M_A$
.
Party B, the second mover, will select a best response to any proposed set of subdistricts. The strategy
![]() $\sigma _B$
is a mapping from the set of valid groupings of subdistricts to a single map,
$\sigma _B$
is a mapping from the set of valid groupings of subdistricts to a single map,
![]() $\widehat {M}_B$
, such that
$\widehat {M}_B$
, such that
Because voters themselves are indivisible and the districts in this setup consist of sets of voters, any game has a fixed number of possible districts. Also, the second mover knows what the first mover has chosen to do. In a finite extensive game with perfect information, such as DCP, there exists a subgame perfect equilibrium solvable using backward induction (Osborne Reference Osborne2004, 173). For the map
![]() $M_A$
selected by Party A, Party B will examine feasible maps,
$M_A$
selected by Party A, Party B will examine feasible maps,
![]() $Q(M_A)$
and will select the map
$Q(M_A)$
and will select the map
![]() $\widehat {M}_B \in Q(M_A)$
maximizing the percentage of seats won by Party B. For every possible map
$\widehat {M}_B \in Q(M_A)$
maximizing the percentage of seats won by Party B. For every possible map
![]() $M_A \in \mathcal {M}$
, Party A can anticipate what map
$M_A \in \mathcal {M}$
, Party A can anticipate what map
![]() $M_B$
Party B would ultimately draw. Therefore, it selects the map
$M_B$
Party B would ultimately draw. Therefore, it selects the map
![]() $\widehat {M}_A$
maximizing the percentage of seats won by Party A subject to Party B’s best-response pairings, with payoff
$\widehat {M}_A$
maximizing the percentage of seats won by Party A subject to Party B’s best-response pairings, with payoff
![]() $ U_A(\sigma _B (\widehat {M}_A))$
.
$ U_A(\sigma _B (\widehat {M}_A))$
.
3.3 A Simple Example: Iowa
A simple example illustrates the DCP framework. Consider a (simplified) map of Iowa, as shown in Figure 1, with 30 equally populated precincts and an overall statewide vote share of 50% for the Democrats and 50% for the Republicans.Footnote 7

Figure 1 Simplified Iowa map. This figure displays a simplified map of Iowa with the state split into 30 equally populated precincts.
Suppose redistricting requires that the state must be divided into five equally populated contiguous districts. Given that each of the 30 precincts has the same population, the state must be divided into five districts of six precincts each. Under these assumptions, there are 27,250 possible maps.
If Democrats redraw the map unilaterally and maximize the number of seats won, they can construct a map where they win four seats and Republicans win one seat. Figure 2a shows one such map (out of many equivalent possibilities) drawn by the Democrats unilaterally. Districts won by Democrats (Republicans) are denoted with a blue (red) outline. In this example, Republicans are packed into District 4, and Democrats win majorities in Districts 1–3 and 5. Conversely, as illustrated in Figure 2b, when Republicans act unilaterally, the opposite result is possible; Republicans win four seats, and Democrats win one.

Figure 2 Examples of final maps for Iowa under URP and under DCP. This figure displays example maps that could emerge from an illustrative Define–Combine Procedure applied to a simplified map of Iowa.
We now apply DCP to this simple example. In the first stage, the defining party will draw a map consisting of 10 contiguous subdistricts, each with three precincts. There are 7,713 valid divisions of this map of Iowa. In the second stage, the combining party selects contiguous pairs of subdistricts to create the final district map. The number of possible combinations in the second stage varies based on the subdistricts defined in the first stage. In this example, the number of combinations varies from 2 to 20 possibilities.
For any possible proposed map, the defining party analyzes the resulting combinations and determines the best response for the combining party. The defining party chooses the map that minimizes the combining party’s utility from the optimal pairing in the subgame. Given the distribution of voters in our running example, Figure 2 presents the results of DCP for this simple example if the Democrats go first, in panel (c), and if the Republicans go first, in panel (d). Multiple equilibria exist, and we present just one graphically. The defined subdistrict plan selected by the Democrats results in three seats for Democrats and two seats for Republicans. The Republicans cannot choose any other combination of these subdistricts to improve the outcome. Similarly, if the Republicans move first, then in equilibrium the Republicans win three seats and the Democrats win two seats. Thus, DCP reduces the advantage conferred to the map drawer. Under URP, there is a three-seat (of five total seats) difference in partisan outcomes depending on who controls the process, while under DCP there is only a one-seat difference depending on who draws the define-stage map. We denote this difference based on first-mover status as
![]() $\delta $
: for URP,
$\delta $
: for URP,
![]() $\delta = 0.8 - 0.2 = 0.6$
, and for DCP,
$\delta = 0.8 - 0.2 = 0.6$
, and for DCP,
![]() $\delta = 0.6 - 0.4 = 0.2$
.
$\delta = 0.6 - 0.4 = 0.2$
.
4 Evaluating the Define–Combine Procedure
4.1 Simulated State Congressional Maps
We use map-drawing algorithms to simulate and compare both redistricting procedures. Unlike other studies of gerrymandering using simulation methods, we focus not on the distribution of possible outcomes in each state but rather on the limit—the most extreme possible map drawn by each party using each process. To identify these maps, we employ the “shortburst” algorithm (Cannon et al. Reference Cannon, Goldbloom-Helzner, Gupta, Matthews and Suwal2023), which begins with a starting map and assigns it a numerical score, such as the number of seats won by a given party. Shortburst maximizes (or minimizes) any objective function defined over a geographic space, and we apply it specifically to the problem of extreme gerrymandering. The algorithm generates a set of N variations of the starting map in a “burst,” calculates a score for each using the same scoring function, and selects the map with the highest score. This burst process repeats until the score stabilizes. As Cannon et al. (Reference Cannon, Goldbloom-Helzner, Gupta, Matthews and Suwal2023) shows, this approach finds more extreme outcomes than those identified by random walks and other distributional approaches.
While the shortburst algorithm is not guaranteed to find the most extreme gerrymander possible in a state, this approach often finds the most extreme known gerrymanders and in many cases achieves gerrymanders that would secure a party’s total victory (e.g., winning all seats in a state). Furthermore, the implementation of shortburst that we apply employs sequential Monte Carlo methods (McCartan and Imai Reference McCartan and Imai2023) designed to explore the space of feasible redistricting plans better than previous Markov chain Monte Carlo methods. These efforts are important because the number of maps in real-world redistricting is large enough to make exhaustive searches of all maps computationally infeasible (see Appendix I of the Supplementary Material for a full discussion and calculations estimating the number of possible maps at each stage).
We first apply shortburst directly to maximize seats won for each party in order to solve for the real-world URP maps that a seat-maximizing redistricter would draw in each state. Second, we develop a custom two-stage algorithm to identify the maps resulting from DCP in each state. Appendix C of the Supplementary Material provides the full details of how we implement these simulations, including pseudocode of the algorithm. We offer condensed descriptions here.
To simulate maps drawn under unilateral redistricting (e.g., maximizing seats won for each party), we apply shortburst for each state and party, running 10 separate sets of simulations. We (1) generate a random starting map, (2) run the shortburst algorithm 2,000 times, generating 10 maps per burst, and (3) save the final map. The scoring function maximizes first the number of seats won by the party and second the party’s vote share in the next closest district.Footnote 8
To simulate DCP, we implement a “nested shortburst” algorithm. For each state and party, we run 20 separate sets of simulations. We (1) generate a random starting map of
![]() $2N$
districts and (2) run the shortburst algorithm 100 times, with 20 maps generated per burst. However, we score each map using a second iteration of the shortburst algorithm, which finds the pairing of districts that maximizes seats for the second party.Footnote
9
This two-step approach directly incorporates both parties’ strategic behavior—maximizing their own seat advantage—at each stage of the game rather than just observing a random set of proposals from the second stage and then choosing the best option. Nonetheless, because the set of possible maps at each stage is large,Footnote
10
we also subsequently validate our key results describing equilibrium behaviors for DCP and URP with an analytical model (see Appendix B of the Supplementary Material) and with grid maps for which we can enumerate all district combinations (see Appendix H.2 of the Supplementary Material).
$2N$
districts and (2) run the shortburst algorithm 100 times, with 20 maps generated per burst. However, we score each map using a second iteration of the shortburst algorithm, which finds the pairing of districts that maximizes seats for the second party.Footnote
9
This two-step approach directly incorporates both parties’ strategic behavior—maximizing their own seat advantage—at each stage of the game rather than just observing a random set of proposals from the second stage and then choosing the best option. Nonetheless, because the set of possible maps at each stage is large,Footnote
10
we also subsequently validate our key results describing equilibrium behaviors for DCP and URP with an analytical model (see Appendix B of the Supplementary Material) and with grid maps for which we can enumerate all district combinations (see Appendix H.2 of the Supplementary Material).
Using election data from the Voting and Election Science Team (2022) merged with 2020 census data from the ALARM Project (Kenny and McCartan Reference Kenny and McCartan2021), we ran simulations for every state with at least two congressional districts. We measure partisanship using the 2020 presidential election results. For each simulation, we use a 1% population deviation constraint (using 2020 total population),Footnote 11 a simple compactness constraint,Footnote 12 and require all districts to be contiguous.
We compare the performance of DCP to two key benchmarks—simulated unilateral redistricting and actual, adopted plans—along a variety of different metrics. The metrics we examine include (1) the advantage, which we will term definer’s advantage, conferred to the map-drawing party by a redistricting procedure (equivalent to
![]() $\delta $
from the Iowa example above); (2) deviation from proportionality; (3) deviation from a fairness target (accounting for geographic biases in a state that might advantage one party); (4) partisan bias induced by a redistricting procedure; and (5) the efficiency gap, which measures the difference in the share of wasted votes between the parties. For proportionality, we examine the difference between the two-party vote share and seat share. For a fairness target, we take the midpoint of the most extreme maps possible under each party’s simulated unilateral redistricting procedure (Benadè et al. Reference Benadè, Procaccia and Tucker-Foltz2023). Partisan bias is the difference between seat share and vote share when votes are split evenly between the parties.Footnote
13
We are agnostic as to the best metric used to evaluate a given redistricting plan; our goal is to show the performance of DCP, and its benefits, across a variety of reasonable measures.
$\delta $
from the Iowa example above); (2) deviation from proportionality; (3) deviation from a fairness target (accounting for geographic biases in a state that might advantage one party); (4) partisan bias induced by a redistricting procedure; and (5) the efficiency gap, which measures the difference in the share of wasted votes between the parties. For proportionality, we examine the difference between the two-party vote share and seat share. For a fairness target, we take the midpoint of the most extreme maps possible under each party’s simulated unilateral redistricting procedure (Benadè et al. Reference Benadè, Procaccia and Tucker-Foltz2023). Partisan bias is the difference between seat share and vote share when votes are split evenly between the parties.Footnote
13
We are agnostic as to the best metric used to evaluate a given redistricting plan; our goal is to show the performance of DCP, and its benefits, across a variety of reasonable measures.
The simulation results reveal that DCP dramatically reduces the partisan advantage conferred to a map maker as compared to URP. Figure 3 presents four maps that compare seats won by each party under the four redistricting procedures. The top two maps show the results of the unilateral redistricting simulations, with Democrats redistricting on the left and Republicans redistricting on the right; the bottom two maps show the results of DCP.

Figure 3 Maps of Simulation Results by Method and Party: These figures report the full set results for URP and DCP simulations. Hexagons labeled “D” indicate Democratic wins; Hexagons labeled “R” indicate Republican wins.
Of the 429 seats redistricted in the simulations, Democrats win 334 (77.9%) when they draw the maps unilaterally in every state. When Republicans draw all maps unilaterally, Democrats win 137 seats (31.9%). The simulations reveal a possible swing of 197 seats between parties through unilateral redistricting. These results represent a theoretical maximum for the shift in seats that could occur due to partisan gerrymandering. Our unilateral simulations are more extreme than those actually drawn in many states considered to be partisan gerrymanders because we impose limited constraints and maximize seats won with a strict vote cutoff of 50% (rather than creating a “toss-up” category). Importantly, these benchmarks are based on one snapshot of voter preferences (2020 Presidential Election vote), so subsequent shifts in voter preferences could produce real-world outcomes outside these bounds. For this reason, we compare the simulated results to actual performance using 2020 congressional election outcomes, so our measures of partisan preferences and election outcomes occur at the same time (November 2020).
DCP dramatically reduces the swing of seats between parties; in many states, the difference in seats won based on who defines and who combines falls to either zero or one. When Democrats draw the Define-stage map, they win 249 (58.0%) seats; when Republicans draw the Define-stage map, Democrats win 211 (49.2%) seats. When calculating the difference state by state (since some parties have a second- rather than first-mover advantage), the swing between parties based on first-mover versus second-mover status amounts to 46 seats, eliminating almost 80% of the swing in seats theoretically possible under unilateral partisan control of redistricting.Footnote 14 Figure 4 highlights the differences between the unilateral redistricting and DCP results. The comparison of light gray hexagons (districts that swing only under URP) to dark gray hexagons (districts that swing also under DCP) captures the reduction in seat swing due to a switch from URP to DCP.

Figure 4 Map of differences in simulation results by party. This map shows how the partisan division of states differ under URP and DCP. Hexagons marked “D” or “R” are seats that are always won by Democrats and Republicans, respectively, in both methods regardless of which party controls the process. Hexagons marked “d”, “r”, or “x” could be won by either party if they controlled URP. Hexagons marked “x” could be won by either party under DCP. The hexagons marked “d” or “r” would be won by Democrats and Republicans, respectively, under DCP.
We also evaluate the performance of URP and DCP under alternative scenarios including (1) uniform statewide vote swings to a 50–50 vote split in each competitive state, (2) uniform nationwide swings to a 50–50 vote split nationwide, and (3) for a selection of state legislative, rather than congressional, district maps. Appendices E.2–E.4 of the Supplementary Material report the results. In each case, DCP continues to dramatically reduce the advantage from unilateral redistricting, eliminating over 80% of the possible swing between parties. We also report outcomes when randomizing the first mover in Appendix E.5 of the Supplementary Material.
Table 1 summarizes results for Definer’s Advantage, along with the other metrics we consider. (We do not report a quantity for Definer’s Advantage for adopted plans because we do not observe seat share under the counterfactual that the out-party controlled the redistricting process.) The next two metrics evaluate the redistricting procedures based on deviations from target outcomes, specifically proportionality and a geometric fairness target (the average of the worst- and best-case map for each party, as defined in Benadè et al. (Reference Benadè, Procaccia and Tucker-Foltz2023)). We evaluate each of these metrics based on which party controlled the redistricting process in each state. For instance, for a simulated unilateral map for the party in power, we calculate the deviation in seat share from the (1) seat share proportional to a state’s vote share and (2) seat share based on the geometric fairness target. The first of these metrics illustrates how much proportional representation would improve based upon a state’s switch to DCP; the second illustrates how much closer to a geometric target (accounting for a map’s geographic biases) a switch to DCP would achieve. Smaller values in the table represent less-biased outcomes.
Table 1 DCP performance versus alternatives. This table reports the performance of DCP compared to unilateral redistricting and adopted plans. Definer’s Advantage for adopted plans is omitted since it would involve interpolating seat share under the scenario where the opposing party held control over the redistricting process. Partisan Bias is calculated only for states with 2020 Democratic Presidential Vote Share between 45% and 55%.

For both metrics, DCP improves upon both the simulated outcomes from URP and adopted plans (rows 2 and 3 in Table 1). We estimate, for example, that if every state drew their map according to a unilateral process controlled by the majority party of the lower house of the state legislature, and then switched to DCP with the same party serving as the definer, deviation from proportionality would be cut by over one third and deviation from the fairness target would be cut by three quarters. Appendix F of the Supplementary Material reports full results broken out by state redistricting procedure. We find that DCP achieves reduced deviations from proportionality compared to enacted maps in states with Legislature or Political redistricting procedures and has comparable or slightly greater deviations from proportionality compared to enacted maps in states with Independent Commissions and Courts or Special Masters. DCP improves upon or matches adopted plans regardless of redistricting procedure in terms of deviations from the geometric fairness target. Figure 5 summarizes these results graphically. For each state in the figure, we plot the actual seat share from the redistricting process and the estimated change under DCP (denoted by the line and arrow). All but two states would move closer to the fairness target after implementing DCP.

Figure 5 Comparing DCP to actual outcomes. This figure displays the comparison between DCP and the actual outcome based on the state’s post-2020 redistricting process. The x-axis reports the midpoint between outcomes when each party acts as a URP. The y-axis reports the seat share. The point where each line originates denotes the projected outcome of the post-2020 redistricting. The point of each arrow denotes the DCP projected outcome. For reference, we also include a 45-degree line (proportional representation) and a line illustrating seat shares for an unbiased but majoritarian electoral system that follows the cube law. The sample includes states with four or more congressional districts and a URP midpoint between 0.3 and 0.7. First mover for DCP is determined based upon the party controlling redistricting or (where not applicable) the majority party in each state.
To determine partisan bias and efficiency gap for adopted plans, we gathered data on each metric from PlanScore.Footnote 15 We replicated the partisan bias and efficiency gap calculations for our simulated URP and DCP maps and compared these measures to the PlanScore estimates. DCP dramatically reduces partisan bias compared to URP. It modestly reduces partisan bias compared to enacted maps, with improvements primarily where legislatures controlled redistricting or political commissions. DCP dramatically reduces the efficiency gap compared to URP and achieves close to the same efficiency gap as for Adopted Plans. When comparing across states based on redistricting method as in Table F.1 in the Supplementary Material, the biggest improvements to efficiency gap occur in states with maps produced by a Legislature or Political Commissions and results are comparable to those in states with Independent Commissions.
Overall, DCP exhibits significant improvements compared to our benchmark procedures and actual maps across a range of different metrics. Importantly, the comparison to enacted maps is not one to one, since our DCP simulations necessarily assume fewer constraints than real-world redistricters face. Thus, the fact that we still observe similar or less extreme maps in our simulations illustrates the powerful tendency of DCP to temper extreme redistricting outcomes. In Appendix B.5 of the Supplementary Material, we also calculate benchmark comparisons between DCP and URP based on an analytical model, and we find that DCP improves upon or matches the benchmark results from URP.
4.2 Compliance with the Voting Rights Act
One potential concern for adopting DCP is the ability to use it to draw maps while complying with the federal Voting Rights Act (VRA), in particular by preserving majority–minority districts. Importantly, the districts produced under DCP will face the same scrutiny as districts created through any other map-drawing process. Under DCP, the judiciary would of course continue to enforce Section 2 of the VRA, and plaintiffs might challenge redistricting plans in court. If a judge finds in favor of a plaintiff, the court may redraw the offending district or districts. As long as the federal judiciary continues to adjudicate claims about adherence to the VRA, resolution of disagreements about majority–minority districts will remain somewhat distinct from any state-level process for producing district maps. So realistically, the federal courts, not DCP or any other process, will ultimately resolve conflicts between the parties over the number of majority–minority districts required to satisfy the VRA.Footnote 16
Nonetheless, map drawers can adjust DCP explicitly to incorporate the creation of majority–minority districts, for instance, by determining the boundaries of majority–minority districts before implementing DCP for the remaining districts. When drawing a fixed number of majority–minority districts, will DCP continue to produce beneficial results if used for the remaining districts? To explore this question, we ran a series of simulations in Georgia, a state with several majority–minority districts and close to equal Democratic and Republican vote shares in the 2020 Presidential election, as follows:
-
1. Using 2020 census data and Voting Tabulation Districts, use the shortburst algorithm to generate four majority-Black districts.
-
2. Freeze the four majority-Black districts in the map.
-
3. Run the unilateral and DCP simulation algorithms to generate the boundaries of the remaining 10 congressional districts, and record the results from each algorithm.
We ran the above procedure 10 times. In each simulation, the boundaries of the four majority-Black districts were different (but were all concentrated in the Atlanta Metro area). Figure 6 shows the results of the simulations. Across all 10 simulations, there are substantial gaps in the number of Democratic seats depending on the party controlling redistricting unilaterally (e.g., a 3–6 seat gap), but much smaller gaps under DCP. In seven of the simulations, both parties reached the same number of Democratic seats, and in three simulations, the parties had a one-seat difference.

Figure 6 Simulation results for VRA-compliant Georgia congressional districts. This figure illustrates the results of URP and DCP simulations in Georgia when we account for VRA-compliant districts by drawing and freezing four districts before initiating the URP and DCP map-drawing processes.
These results demonstrate that if majority–minority districts can be drawn and then frozen in place, DCP can still produce an equitable result that reduces partisan gerrymandering in the remainder of the state.
5 Robustness of Results
We evaluate two types of threats to the validity of our state-by-state simulation results: (1) generalizability concerns and (2) computation/simulation concerns. First, though DCP appears to perform well in the states we examine, this success might not extend to other settings. Second, due to the large number of possible maps to consider at both the Define and the Combine stages, one might fear that our simulations do not discover the most extreme maps and therefore overstate reductions in bias due to DCP.
To evaluate the generalizability of our results, we use grid maps allowing for variation in partisan composition, geographic clustering by party, and the parties’ objective functions. We find that DCP continues to reduce both the Definer’s advantage and the partisan bias from redistricting regardless of variation in these characteristics. Appendix H of the Supplementary Material provides a detailed account of our findings for each.
To validate our simulations, we (1) developed an analytical model and analyzed each party’s optimal strategy for the special case of redistricting without geographic constraints in Appendix B of the Supplementary Material and (2) compared key findings from real-world simulations to findings from fully solvable grid maps (e.g., obviating the need for short burst since all maps can be enumerated) in Appendices H.2 and Appendix J of the Supplementary Material.
Solving the analytical model illustrates the optimal behavior of each party, and reveals when DCP effectively reduces partisan gerrymandering with no geographic constraints: the clearest improvements under DCP compared to URP occur when a party with a minority of voters in a state controls the redistricting process.
Under unilateral redistricting, the minority party can secure a share of districts equal to double their population share by spreading their own voters evenly into as many districts as possible while maintaining a narrow majority. The unilateral redistricter will pack the remaining voters supporting the other party into the remaining districts. Thus, a minority party that redistricts unilaterally can win more than half the seats. In fact, a narrow minority can win a large majority of the seats in a state (e.g., a party with
![]() $V_A = 40\%$
can win a seat share of
$V_A = 40\%$
can win a seat share of
![]() $80\%$
).
$80\%$
).
DCP tempers the ability of the minority party as first mover (Definer) to gerrymander. In fact, when the majority party is the second mover (Combiner) under DCP, the majority party wins strictly more seats compared to the URP case. When the Combiner has a large majority of the vote, the optimal approach for the Definer is to “self-pack,” creating subdistricts consisting entirely of the minority party. In this case, both parties win seats proportional to their share of the vote. When the Combiner holds a narrower majority of vote share (specifically, between one third and one half of the statewide vote), the Definer instead adopts a “cracking” strategy and can win more seats than their proportional share of the vote but fewer than what they would win in the unilateral case. Thus, our analytical results illustrate how DCP helps ensure that the party with a majority of voters will be more likely to win a majority of seats, an intuitive fairness benchmark and a characteristic of partisan symmetry. Appendix B of the Supplementary Material provides the full analytical solutions, sketches proofs, and illustrates the seats-votes curves for each party. Appendix B.5 of the Supplementary Material evaluates DCP and URP along key fairness metrics for the analytical model and shows that DCP performs better to or equal to URP along these benchmarks in all cases. Crucially, this analysis illustrates DCP’s advantages totally independent of computer simulations.
Yet the analytical model without geographic constraints does not capture all the ways in which DCP may improve upon URP precisely because it does not take geography into account. By combining the insights from the analytical model and the fully solved grid simulations, we also can illustrate how DCP interacts with geographic constraints to constrain gerrymandering further. The key insight is that, with geographic constraints in place, DCP requires the Definer to create smaller subdistricts than the final districts (e.g., half the size in population), constraining how freely parties can combine disparate populations to gerrymander. This additional constraint reduces the ability to gerrymander for the Definer regardless of statewide vote share. Appendix J of the Supplementary Material provides a detailed account of this finding. Taken together, the fully solvable grid maps, the robustness to variation of map characteristics, and the insights from the analytical model all support the account that our real-world simulations accurately capture the performance of DCP as compared to URP.
6 Conclusion
DCP features simple rules, clear strategies for each party, and an efficient framework that can be implemented in every state. One obstacle to implementation for past theoretical approaches has been the difficulty for decision-makers in either party to predict outcomes in the real world. DCP, as we have demonstrated, can be applied to real-world geographic data, which allows analysts to predict outcomes and reduce uncertainty surrounding the redistricting process. Furthermore, DCP significantly reduces the advantages conferred to the redistricting party and results in maps more likely to reflect the will of voters. These advantages hold up (1) across a variety of different contexts reflecting the political and geographic heterogeneity of the states, (2) for a number of different measures of a map’s level of bias, and (3) when perturbing levels of statewide partisanship, the objective functions of redistricters, and geographic clustering.
There are many challenges in using automated algorithms to aid in the redistricting process (Cho and Cain Reference Cho and Cain2020). In some cases, advances in computing power and the ability of politicians to consider a large range of maps exacerbate partisan gerrymandering, rather than alleviating it, as partisan mapmakers use map-drawing algorithms to devise increasingly gerrymandered maps. DCP provides an approach that utilizes advances in computing to produce less biased maps—ones where the process-based algorithm itself constrains partisan motives.
Political parties will almost always oppose ceding power, but this is doubly so when the choices they face require embracing significant uncertainty about future political outcomes. Because DCP is a two-stage game, solvable with existing computing resources, it represents a step toward providing an alternative mechanism to court-, legislature-, or commission-based redistricting that is feasible to implement. This framework offers parties the autonomy to respect communities of interest, geographic boundaries, and other political concerns—that is, to internalize the wide range of factors that play important roles in decisions about redistricting—while nonetheless tempering the partisan biases that emerge during redistricting. By involving both parties but setting them in opposition to each other, rather than requiring bipartisan cooperation or independent third-party mediators, DCP offers a partisan solution to the extraordinarily partisan process that is redistricting.
Acknowledgments
We would like to thank the three anonymous reviewers and the editor for their thoughtful comments and discussion. We would also like to thank Jowei Chen, Justin de Benedictis-Kessner, Katie Einstein, David Glick, Richard Engstrom, Gary King, Chris Kenny, Jonathan Rodden, Chris Warshaw, and audiences at the Midwest Political Science Association Conference, the MIT Election Data and Science Lab (MEDSL) Workshop, the Harvard Kennedy School Faculty Lunch Workshop, and the “Redistricting Algorithms, Law, and Policy” Exploratory Seminar hosted by the Harvard Radcliffe Institute for their feedback. We would also like to thank the staff at the Boston University Shared Computing Cluster for generous computational assistance.
Funding
This work was supported by the Hariri Institute for Computing at Boston University.
Data Availability Statement
Replication materials can be found on the Political Analysis Harvard Dataverse for Palmer, Schneer, and DeLuca (Reference Palmer, Schneer and DeLuca2023) at https://doi.org/10.7910/DVN/XBYFE1.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2023.39.