Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-14T19:34:57.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Coactions and skew products for topological quivers

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  22 May 2024

Lucas Hall Open the ORCID record for Lucas Hall [Opens in a new window]
Lucas Hall*
Affiliation:
Department of Mathematics, University of Haifa, Haifa, Israel Department of Mathematics, Michigan State University, East Lansing, Michigan, US
*
Email: hallluc1@msu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a cocycle on a topological quiver by a locally compact group, the author constructs a skew product topological quiver and determines conditions under which a topological quiver can be identified as a skew product. We investigate the relationship between the 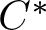${C^*}$-algebra of the skew product and a certain native coaction on the 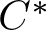${C^*}$-algebra of the original quiver, finding that the crossed product by the coaction is isomorphic to the skew product. As an application, we show that the reduced crossed product by the dual action is Morita equivalent to the 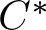${C^*}$-algebra of the original quiver.

Keywords

G-bundlecrossed productcoactiontopological quiver

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C. and Renault, J., Amenable Groupoids, Monographies de L’Enseignement Mathématique [Monographs of L’Enseignement Mathématique], Vol. 36, L’Enseignement Mathématique, Geneva, 2000. With a foreword by Georges Skandalis and Appendix B by E. Germain, MR1799683.Google Scholar
Blanchard, E., Déformations de $C^*$-algèbres de Hopf, French, with English and French summaries, Bull. Soc. Math. France 124(1) (1996), 141–215 MR1395009.CrossRefGoogle Scholar
Deaconu, V., Kumjian, A. and Quigg, J., Group actions on topological graphs, Ergodic Theory Dynam. Systems 32(5) (2012), 1527–1566. DOI: 10.1017/S014338571100040X, MR2974209.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S. and Quigg, J., Maximal coactions, Internat. J. Math. 15(1) (2004), 47–61.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., A categorical approach to imprimitivity theorems for $C^*$-dynamical systems, Mem. Amer. Math. Soc. 180 (2006), .Google Scholar
Gross, J. L. and Tucker, T. W., Topological Graph theory, Wiley-Interscience Series in Discrete Mathematics and Optimization, (John Wiley & Sons, Inc., New York, 1987), A Wiley-Interscience Publication. MR898434.Google Scholar
Hall, L., Kaliszewski, S., Quigg, J. and Williams, D. P., Groupoid Semidirect Product Fell Bundles II—Principal Actions Stabi lization, Indiana Univ. Math. J. 72(3) (2023), 1147–1173. doi:10.1512/iumj.2023.72.9447CrossRefGoogle Scholar
Huef, A., Quigg, J., Raeburn, I. and Williams, D. P., Full and reduced coactions of locally compact groups on $C^\ast $-algebras, Expo. Math. 29(1) (2011), 3–23 10.1016/j.exmath.2010.06.002. MR2785543.CrossRefGoogle Scholar
Husemoller, D., Graduate Texts in Mathematics, (3rd ed.), Volume 20, (Springer-Verlag, New York, 1994), MR1249482.Google Scholar
Kaliszewski, S. and Quigg, J., Coactions and skew products of topological graphs, Integral Equations Operator Theory 75(2) (2013), 187–196 10.1007/s00020-012-2022-4. MR3008922.CrossRefGoogle Scholar
Kaliszewski, S., Quigg, J. and Raeburn, I., Skew products and crossed products by coactions, J. Operator Theory 46(2) (2001), 411–433 MR1870415.Google Scholar
Kaliszewski, S., Quigg, J. and Robertson, D., Functoriality of Cuntz-Pimsner correspondence maps, J. Math. Anal. Appl. 405(1) (2013), 1–11 10.1016/j.jmaa.2013.02.069. MR3053482.CrossRefGoogle Scholar
Kaliszewski, S., Quigg, J. and Robertson, D., Coactions on Cuntz-Pimsner algebras, Math. Scand. 116(2) (2015), 222–249 10.7146/math.scand.a-21161. MR3367428.CrossRefGoogle Scholar
Katsura, T., A Construction of $C^*$-algebras from $C^*$-correspondences, Advances in Quantum Dynamics (South Hadley, MA, 2002), Contemp. Math. 335 (2003), 173–182. Amer. Math. Soc. Providence, RI, 10.1090/conm/335/06007, MR2029622.Google Scholar
Katsura, T., A class of $C^\ast $-algebras generalizing both graph algebras and homeomorphism $C^\ast $-algebras. I. Fundamental results, Trans. Amer. Math. Soc. 356(11) (2004), 4287–4322 10.1090/S0002-9947-04-03636-0. MR2067120.CrossRefGoogle Scholar
Muhly, P. S. and Tomforde, M., Topological quivers, Internat. J. Math. 16(7) (2005), 693–755 10.1142/S0129167X05003077. MR2158956.CrossRefGoogle Scholar
Munkres, J. R., Topology, (2nd edition of [MR0464128]), (Prentice Hall, Inc., Upper Saddle River, NJ, 2000). MR3728284.Google Scholar
Palais, R. S., On the existence of slices for actions of non-compact Lie groups, Ann. of Math. 73(2) (1961), 295–323 10.2307/1970335. MR126506.CrossRefGoogle Scholar
Raeburn, I., Graph Algebras, CBMS Regional Conference Series in Mathematics, Vol. 103, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2005. MR2135030.CrossRefGoogle Scholar
Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-trace $C^*$-algebras, Mathematical Surveys and Monographs, Volume 60, (American Mathematical Society, Providence, RI, 1998), MR1634408.Google Scholar
Williams, D. P., A Tool Kit for Groupoid $C^*$-algebras, Mathematical Surveys and Monographs, Volume 241, (American Mathematical Society, Providence, RI, 2019). MR3969970.Google Scholar