Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McLean, K. R.
1982.
Rigid Artinian rings.
Proceedings of the Edinburgh Mathematical Society,
Vol. 25,
Issue. 1,
p.
97.
Beidar, K. I.
Latyshev, V. N.
Markov, V. T.
Mikhalev, A. V.
Skornyakov, L. A.
and
Tuganbaev, A. A.
1987.
Associative rings.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1855.
Ferrero, Celestina Cotti
1987.
Near-Rings and Near-Fields, Proceedings of a Conference held at the University of Tübingen, F.R.G..
Vol. 137,
Issue. ,
p.
63.
Friger, Michael
1994.
Strongly rigid and I-rigid rings.
Communications in Algebra,
Vol. 22,
Issue. 5,
p.
1833.
Artemovich, O. D.
1998.
On I-Rigid and q-Rigid Rings.
Ukrainian Mathematical Journal,
Vol. 50,
Issue. 7,
p.
1125.
Friger, Michael
2001.
TORSION-FREE RINGS WITH FINITE AUTOMORPHISM GROUPS.
Communications in Algebra,
Vol. 29,
Issue. 2,
p.
503.




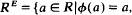 for each φɛ
for each φɛ