Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-20T00:28:03.070Z Has data issue: false hasContentIssue false
  • English
  • Français

Some inequalities for norm unitaries in Banach algebras

Published online by Cambridge University Press:  20 January 2009

M. J. Crabb  and
J. Duncan
M. J. Crabb
Affiliation:
University of Glasgow
J. Duncan
Affiliation:
University of Stirling
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a complex unital Banach algebra. An element u∈A is a norm unitary if

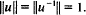
(For the algebra of all bounded operators on a Banach space, the norm unitaries arethe invertible isometries.) Given a norm unitary u∈A, we have Sp(u)⊃Γ, where Sp(u) denotes the spectrum of u and Γ denotes the unit circle in C. If Sp(u)≠Γ we may suppose, by replacing eiθu, that 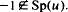. Then there exists h ∈ A such that

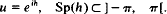
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 21 , Issue 1 , March 1978 , pp. 17 - 23
Copyright
Copyright © Edinburgh Mathematical Society 1978

References

REFERENCES

(1) Bernstein, S. N., The extension of properties of trigonometric polynomials to entire functions of finite degree, Izv. Akad. Nauk, 12 (1948), 421–444 (Russian).Google Scholar
(2) Boas, R. P., Entire functions (Academic Press, 1954).Google Scholar
(3) Bollobás, B., The numerical range in Banach algebras and complex functions of exponential type, Bull. London Math. Soc. 3 (1971), 27–33.CrossRefGoogle Scholar
(4) Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and of elements of normed algebras (London Math. Soc. Lecture Note Series, No. 2, Cambridge University Press, 1971).CrossRefGoogle Scholar
(5) Harris, L. A. and Kaup, W., Linear algebraic groups in infinite dimensions, Illinois J. Math. 21 (1977), 666–674.CrossRefGoogle Scholar
(6) Varopoulos, N. TH., Sur les ensembles parfaits et les series trigonometriques, C.R. Acad. Sci. Paris 260 (1965), 3831–3834.Google Scholar