Global attractivity and extinction for Lotka–Volterra systems with infinite delay and feedback controls
Published online by Cambridge University Press: 02 April 2015
Abstract
The paper deals with a multiple species Lotka–Volterra model with infinite distributed delays and feedback controls, for which we assume a weak form of diagonal dominance of the instantaneous negative intra-specific terms over the infinite delay effect in both the population variables and controls. General sufficient conditions for the existence and attractivity of a saturated equilibrium are established. When the saturated equilibrium is on the boundary of 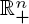 , sharper criteria for the extinction of all or part of the populations are given. While the literature usually treats the case of competitive systems only, here no restrictions on the signs of the intra- and inter-specific delayed terms are imposed. Moreover, our technique does not require the construction of Lyapunov functionals.
, sharper criteria for the extinction of all or part of the populations are given. While the literature usually treats the case of competitive systems only, here no restrictions on the signs of the intra- and inter-specific delayed terms are imposed. Moreover, our technique does not require the construction of Lyapunov functionals.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 145 , Issue 2 , April 2015 , pp. 301 - 330
- Copyright
- Copyright © Royal Society of Edinburgh 2015
- 8
- Cited by

