Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-07T14:44:13.126Z Has data issue: false hasContentIssue false
  • English
  • Français

On inscribed trapezoids and affinely 3-regular maps

Part of: Differential topology Classical differential geometry

Published online by Cambridge University Press:  12 May 2023

Florian Frick  and
Michael Harrison Open the ORCID record for Michael Harrison [Opens in a new window]
Florian Frick
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, United States Institute of Mathematics, Freie Universität Berlin, Arnimallee 2, 14195 Berlin, Germany (frick@cmu.edu)
Michael Harrison
Affiliation:
Institute for Advanced Study, 1 Einstein Drive, Princeton, New Jersey 08540, United States (mah5044@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that any embedding $\mathbb {R}^d \to \mathbb {R}^{2d+2^{\gamma (d)}-1}$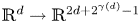 inscribes a trapezoid or maps three points to a line, where $2^{\gamma (d)}$ 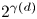is the smallest power of $2$ 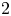satisfying $2^{\gamma (d)} \geq \rho (d)$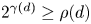, and $\rho (d)$ 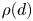denotes the Hurwitz–Radon function. The proof is elementary and includes a novel application of nonsingular bilinear maps. As an application, we recover recent results on the nonexistence of affinely $3$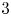-regular maps, for infinitely many dimensions $d$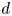, without resorting to sophisticated algebraic techniques.

Keywords

inscribed trapezoidsk-regular mapsnonsingular bilinear mapsHurwitz–Radon function

MSC classification

Primary: 53A07: Higher-dimensional and -codimensional surfaces in Euclidean $n$-space
Secondary: 57R40: Embeddings
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 9
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. F.. Vector fields on spheres. Ann. Math. 75 (1962), 603–632.CrossRefGoogle Scholar
Aslam, J., Chen, S., Frick, F., Saloff-Coste, S., Setiabrata, L. and Thomas, H.. Splitting loops and necklaces: variants of the square peg problem. Forum Math. Sigma 8 (2020), E5.CrossRefGoogle Scholar
Berger, M. and Friedland, S.. The generalized Radon–Hurwitz numbers. Compos. Math. 59 (1986), 113–146.Google Scholar
Blagojević, P. V. M., Cohen, F. R., Crabb, M. C., Lück, W. and Ziegler, G. M.. Equivariant cohomology of configuration spaces mod 2: the state of the art (Cham: Springer, 2021).CrossRefGoogle Scholar
Borsuk, K.. On the $k$-independent subsets of the Euclidean space and of the Hilbert space. Bull. Acad. Polon. Sci. Cl. III 5 (1957), 351–356.Google Scholar
Bogatyi, S. A.. $k$-Regular maps into Euclidean spaces and the Borsuk-Boltyanskii problem. Sbornik Math. 193 (2002), 73.CrossRefGoogle Scholar
Boltyansky, V. G., Ryzhkov, S. S. and Shashkin, Yu. A.. On k-regular embeddings and their applications to the theory of approximation of functions. Usp. Mat. Nauk 15 (1960), 125–132.Google Scholar
Buczyński, J., Januszkiewicz, T., Jelisiejew, J. and Michałek, M.. Constructions of $k$-regular maps using finite local schemes. J. Eur. Math. Soc. 21 (2019), 1775–1808.CrossRefGoogle Scholar
Chisholm, M. E.. $k$-regular mappings of $2^n$-dimensional Euclidean space. Proc. Am. Math. Soc. 74 (1979), 187–190.Google Scholar
Cohen, F. R. and Handel, D.. $k$-regular embeddings of the plane. Proc. Am. Math. Soc. 72 (1978), 201–204.Google Scholar
Frick, F. and Harrison, M.. Coupled embeddability. Bull. London Math. Soc. 54 (2022), 1609–1629.CrossRefGoogle Scholar
Frick, F. and Harrison, M.. Spaces of embeddings: nonsingular bilinear maps, chirality, and their generalizations. Proc. Am. Math. Soc. 150 (2022), 423–437.Google Scholar
Greene, J. and Lobb, A.. The rectangular peg problem. Ann. Math. 194 (2021), 509–517.CrossRefGoogle Scholar
Handel, D.. Obstructions to $3$-regular embeddings. Houston J. Math. 5 (1979), 339–343.Google Scholar
Handel, D.. Some existence and nonexistence theorems for $k$-regular maps. Fundam. Math. 109 (1980), 229–233.CrossRefGoogle Scholar
Handel, D.. $2k$-regular maps on smooth manifolds. Proc. Am. Math. Soc. 124 (1996), 1609–1613.CrossRefGoogle Scholar
Handel, D. and Segal, J.. On $k$-regular embeddings of spaces in Euclidean space. Fundam. Math. 106 (1980), 231–237.CrossRefGoogle Scholar
Harrison, M.. Skew flat fibrations. Math. Z. 282 (2016), 203–221.CrossRefGoogle Scholar
Harrison, M.. Introducing totally nonparallel immersions. Adv. Math. 374 (2020), 251–286.CrossRefGoogle Scholar
Harrison, M.. Fibrations of $\mathbb {R}^3$ by oriented lines. Algebr. Geom. Topol. 21 (2021), 2899–2928.CrossRefGoogle Scholar
Hopf, H.. Ein toplogischer Beitrag zur reellen algebra. Comment. Math. Helv. 13 (1940), 219–239.CrossRefGoogle Scholar
James, I. M.. Euclidean models of projective spaces. Bull. London Math. Soc. 3 (1971), 257–276.CrossRefGoogle Scholar
James, I. M.. On the immersion problem for real projective spaces. Bull. Am. Math. Soc. 69 (1963), 231–238.CrossRefGoogle Scholar
Lam, K. Y.. Construction of nonsingular bilinear maps. Topology 6 (1967), 423–426.CrossRefGoogle Scholar
Lam, K. Y.. On bilinear and skew-linear maps that are nonsingular. Q. J. Math. 19 (1968), 281–288.CrossRefGoogle Scholar
Lam, K. Y.. Non-singular bilinear maps and stable homotopy classes of spheres. Math. Proc. Cambridge Philos. Soc. 82 (1977), 419–425.CrossRefGoogle Scholar
Lam, K. Y.. Some interesting examples of nonsingular bilinear maps. Topology 16 (1977), 185–188.CrossRefGoogle Scholar
Lam, K. Y.. KO-equivalences and existence of nonsingular bilinear maps. Pac. J. Math. 82 (1979), 145–154.CrossRefGoogle Scholar
Lam, K. Y.. Some new results on composition of quadratic forms. Invent. Math. 79 (1985), 467–474.CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S.. On fibrations with flat fibres. Bull. London Math. Soc. 45 (2013), 625–632.CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S.. Hopf fibrations and Hurwitz–Radon numbers. Math. Intell. 38 (2016), 11–18.CrossRefGoogle Scholar