Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kirchg�ssner, Klaus
and
Lankers, Katharina
1993.
Structure of permanent waves in density-stratified media.
Meccanica,
Vol. 28,
Issue. 4,
p.
269.
Sun, S.M.
and
Shen, M.C.
1994.
Exponentially small estimate for a generalized solitary wave solution to the perturbed K−dV equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 23,
Issue. 4,
p.
545.
Dias, Frédéric
1995.
Asymptotic Modelling in Fluid Mechanics.
Vol. 442,
Issue. ,
p.
67.
Néel, M. C.
and
Lyubimov, D.
1995.
Periodic solutions for differential equations of order three, with application to heat‐flux induced convection.
Mathematical Methods in the Applied Sciences,
Vol. 18,
Issue. 14,
p.
1133.
Bridges, Thomas J.
and
Mielke, Alexander
1995.
A proof of the Benjamin-Feir instability.
Archive for Rational Mechanics and Analysis,
Vol. 133,
Issue. 2,
p.
145.
1996.
A plethora of solitary gravity-capillary water waves with nearly critical Bond and Froude numbers.
Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 354,
Issue. 1707,
p.
575.
Il'ichev, A. T.
1996.
Solitary waves in a cold plasma.
Mathematical Notes,
Vol. 59,
Issue. 5,
p.
518.
Lombardi, Eric
1996.
Homoclinic orbits to small periodic orbits for a class of reversible systems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 5,
p.
1035.
Bakholdin, I. B.
1996.
Nonlinear resonances and wave jumps in media with higher-order dispersion.
Fluid Dynamics,
Vol. 31,
Issue. 4,
p.
573.
Il'Ichev, Andrej
1996.
Steady waves in a cold plasma.
Journal of Plasma Physics,
Vol. 55,
Issue. 2,
p.
181.
1996.
A multiplicity of localized buckling modes for twisted rod equations.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 452,
Issue. 1954,
p.
2467.
Iooss, Gérard
and
Kirrmann, Pius
1996.
Capillary gravity waves on the free surface of an inviscid fluid of infinite depth. Existence of solitary waves.
Archive for Rational Mechanics and Analysis,
Vol. 136,
Issue. 1,
p.
1.
Bruno, A. D.
1997.
Power geometry.
Journal of Dynamical and Control Systems,
Vol. 3,
Issue. 4,
p.
471.
James, Guillaume
1997.
Small amplitude steady internal waves in stratified fluids.
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 43,
Issue. 1,
p.
65.
Bruno, A. D.
1997.
Power Geometry.
Journal of Dynamical and Control Systems,
Vol. 3,
Issue. 4,
p.
471.
Kichenassamy, Satyanad
1997.
Existence of solitary waves for water-wave models.
Nonlinearity,
Vol. 10,
Issue. 1,
p.
133.
Bridges, Thomas J
1998.
Toral-equivariant partial differential equations and quasiperiodic patterns.
Nonlinearity,
Vol. 11,
Issue. 3,
p.
467.
Sun, S. M.
1998.
On the Oscillatory Tails with Arbitrary Phase Shift for Solutions of the Perturbed Korteweg--de Vries Equation.
SIAM Journal on Applied Mathematics,
Vol. 58,
Issue. 4,
p.
1163.
Champneys, A. R.
van der Heijden, G. H. M.
and
Thompson, J. M. T.
1998.
The Spatial Complexity of Localized Buckling in Rods with Noncircular Cross Section.
SIAM Journal on Applied Mathematics,
Vol. 59,
Issue. 1,
p.
198.
Brevdo, L.
and
Kirchgässner, K.
1999.
Structure formation in a zonal barotropic current: a treatment via the centre manifold reduction.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 455,
Issue. 1986,
p.
2021.

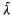 is close to 1. The Bond number
is close to 1. The Bond number 