INTRODUCTION
In most radioactive isotope systems used for dating, a daughter product is available for measurement so that an absolute age can be calculated. Unfortunately, for radiocarbon (14C) dating, this is not the case as the nitrogen produced by 14C decay is not captured in most materials and, even if it were, this decay product would be swamped by the pervasive nature of nitrogen in the Earth system. Therefore, calibration against 14C measurements from known-age or independently dated material is critical for providing a correction for changes in 14C concentration within atmospheric and marine carbon reservoirs.
The IntCal Working Group (IWG) has endeavored to provide 14C calibration curves at semi-regular intervals since 2004, building on pioneering work by Stuiver et al. (Reference Stuiver, Kromer, Becker and Ferguson1986, Reference Stuiver, Reimer, Bard, Beck, Burr, Hughen, Kromer, McCormac, Van der Plicht and Spurk1998a). Each new curve release incorporated all calibration data available at the time of construction that met the IntCal criteria (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Brown, Buck, Edwards and Friedrich2013a) using robust curve construction methods. Inevitably, new datasets and improved understanding of the natural fluctuations in 14C in the atmosphere and oceans have resulted in an ongoing process of refinement, with curves (or particular datasets) becoming obsolete over time and replacement versions being released. In this latest iteration of the Northern Hemisphere IntCal curve, several new screening procedures were introduced to increase the transparency of data and metadata associated with a large influx of, mostly, annually resolved 14C measurements from tree rings. Including the large number of these data points that meet the published IntCal criteria (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Brown, Buck, Edwards and Friedrich2013a) and the additional screening procedures described below, allows for wider geographic coverage in the tree-ring datasets than in previous versions (Figure 1) and improves the data density, and thus robustness, of the calibration curve. Equally importantly, the new approach makes subtle alterations to the shape of the curve for a more accurate representation of 14C concentrations across selected time periods not previously possible using multiyear tree-ring samples (blocks). Beyond the last 12,310 years for which securely dated tree-ring data are available, annual and multiyear tree-ring data from floating sequences offer new ways to resolve and secure coarser-resolution paleoenvironmental sequences. Thus, back to ca. 13,910 cal BP, where sufficient, continuous 14C measurements of tree-ring chronologies exist, IntCal20 is fully atmospheric. For the older part of the timescale it was decided that the revised and extended atmospheric Lake Suigetsu varved sediment macrofossil record still lacked sufficient corroboration to be used as a stand-alone atmospheric record. Thus, this part of IntCal20 comprises statistically integrated evidence from floating tree-ring chronologies, terrestrial macrofossils from lake sediments, foraminifera from marine sediments, speleothems, and corals, using improved evaluation of the time and location variable 14C offsets from the atmosphere (reservoir ages, dead carbon fractions) for each dataset. All these data have been combined using a newly developed Bayesian spline approach which has been adapted to optimize the incorporation of a large number of annual tree rings.
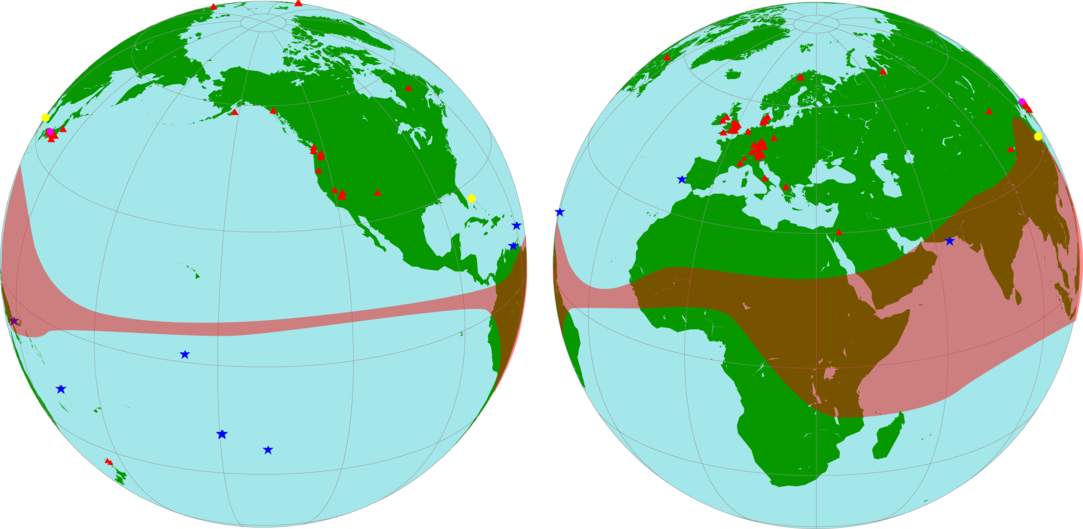
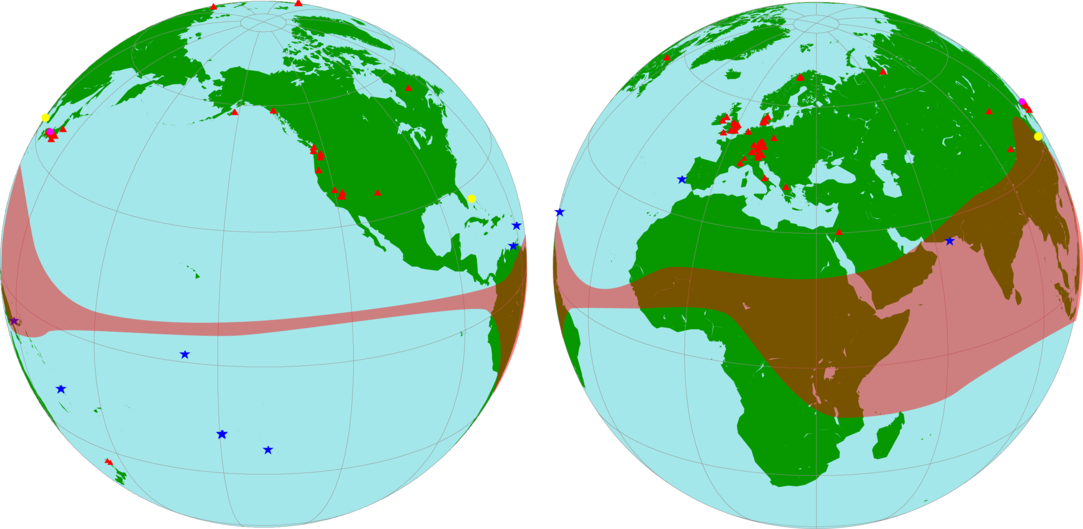
Figure 1 Global representation of the datasets included in the Northern Hemisphere IntCal20 calibration curve: tree rings (red triangles), marine (blue stars), speleothem (yellow circles), Lake Suigetsu (magenta circle). The extent of the Inter-Tropical Convergence Zone (ITCZ) is shown as a shaded band after the reconstruction of the zonal boundaries based on wind data Hogg et al. (Reference Hogg, Heaton, Hua, Palmer, Turney, Southon, Bayliss, Blackwell, Boswijk, Bronk Ramsey, Pearson, Petchey, Reimer, Reimer and Wacker2020 in this issue). (Please see electronic version for color figures.)
IntCal20 is one of a collection of three calibration curves. IntCal20 is intended for the calibration of Northern Hemisphere atmospheric samples; SHCal20 the calibration of Southern Hemisphere atmospheric samples (Hogg et al. Reference Hogg, Heaton, Hua, Palmer, Turney, Southon, Bayliss, Blackwell, Boswijk, Bronk Ramsey, Pearson, Petchey, Reimer, Reimer and Wacker2020 in this issue); and Marine20 (with application of a local reservoir adjustment) the calibration of marine samples (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen, Kromer, Reimer, Adkins, Burke, Cook, Olsen and Skinner2020a in this issue).
THE DATASETS
The IWG has compiled an extensive database of published and previously unpublished data for the construction of the new curves which is available at http://intcal.org. A list of the datasets included in the northern hemispheric curve and references for these datasets are given in Table S2. Some corrections to datasets included in previous IntCal curves have been made and are given here or in accompanying papers. The details of the datasets used for the Southern Hemisphere calibration curve SHCal20 and any special considerations are given in Hogg et al. (Reference Hogg, Heaton, Hua, Palmer, Turney, Southon, Bayliss, Blackwell, Boswijk, Bronk Ramsey, Pearson, Petchey, Reimer, Reimer and Wacker2020 in this issue). All ages in this paper and the database are reported relative to AD 1950 (= 0 BP, before present). Conventional 14C ages are given in units “BP” and calendar or calibrated ages as “cal BP” or cal kBP (thousands of calibrated years before present). Historical AD/BC dates (without the year zero) are also used for known age events and dendrochronological dated wood in some cases. Further, all quoted uncertainties on values or offsets, e.g. 14 ± 3 14C yr, refer to the 1σ level.
Terrestrial 14C Archives and Considerations
Tree Rings
Data criteria
A total of 220 tree-ring datasets from both published and previously unpublished sources were screened for possible inclusion in the IntCal20 curve for the Northern Hemisphere. Where possible, the research group that had produced each dataset was asked whether they considered their data suitable for inclusion in IntCal20. A number of datasets were either rejected at this stage (because of known problems with dendrochronology, the dissection of tree-ring series for 14C dating, the laboratory measurement, or the extant laboratory archive), or reserved for comparison purposes (e.g. where laboratories considered that higher quality data was available for a particular time period, or a laboratory problem was suspected but is still under investigation).
Datasets were then assessed against the relevant published IntCal criteria (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Brown, Buck, Edwards and Friedrich2013a):
1. Laboratory methodologies
a. Pretreatment is specified,
b. Evidence of background or blank correction is provided,
c. Details of uncertainty calculations are provided,
d. Data from relevant intercomparison exercises, known-age samples, or reproducibility with existing calibration datasets are provided.
In addition, all new data accepted into IntCal20 were required to include all quantifiable sources of uncertainty either through a laboratory error multiplier or additional variance.
All laboratories provided at least some information covering all these categories. Pretreatment was generally fully specified, but the level of detail of background or blank correction and uncertainty calculations varied greatly between laboratories. Approaches to replication also varied. Overall more than one measurement on the same cellulose preparation is available for ca. 10% of dated tree-ring samples, although more than 95% of these are intra-laboratory replicates undertaken by QL- (set 1) and ETH- (set 69). Whole-process intra-laboratory replicates are available for only ca. 3% of dated tree-ring samples, almost 60% of which were undertaken by UCIAMS- (set 8), although inter-laboratory replicates are available for another ca. 3% (Usoskin et al. Reference Usoskin, Kromer, Ludlow, Beer, Friedrich, Kovaltsov, Solanki and Wacker2013; Bayliss et al. Reference Bayliss, Marshall, Friedrich, Dee, Heaton, Bollhanger and Wacker2020 in this issue; A. Sookdeo, personal communication; Pearson et al. Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue; Friedrich et al. Reference Friedrich, Kromer, Wacker, Olsen, Remmele, Lindauer, Land and Pearson2020 in this issue).
2. Dendrochronology
a. Sample derives from a single tree,
b. Methodology used for dating is specified,
c. Details of ring(s) sampled in a particular tree are specified,
d. Cross-matching of tree ring-width series is fully documented,
e. Cross-dating of tree ring-width series is fully documented (including version of reference chronologies used),
f. Raw ring-widths are published or deposited in a secure publicly accessible archive.
The criteria were expanded for this iteration of the curve to include dendrochronologies derived from δ18O pattern matching. This can be used in the same way as ring-width dendrochronology to produce tree-ring sequences on a calendar timescale and tested using similar statistical criteria to those employed for traditional tree-ring dating (Nakai et al. Reference Nakai, Okada, Sano and Nakatsuka2018; Loader et al. Reference Loader, McCarroll, Miles, Young, Davies and Bronk Ramsey2019).
A concerted effort was made to gather the required information for every new dataset under consideration for IntCal20 (and we thank the many dendrochronologists from all around the world who resolved our queries). At this stage, a number of datasets were rejected either because the dendrochronology was considered to be insecure or the dissection of the tree-ring series for 14C dating was problematic. Other datasets have been reserved for comparison purposes (when insufficient information on the dendrochronology was available to us). Generally, considerable confusion was caused by the use of Historical BC (without a year zero) and Astronomical BC (with a year zero) in different laboratories and by different tree-ring software packages. It is essential that the calendar scale used is clear.
At this stage a small number of amendments/corrections were made to datasets that had been included in IntCal13:
1. Inconsistencies in block definition (e.g. which rings were sampled) were identified for the Amstel Castle data (van der Plicht et al. Reference van der Plicht, Jansma and Kars1995; dataset 4/2), which could not be resolved and so this dataset has been removed from IntCal20.
2. A small number of data points in the Heidelberg datasets have been corrected (dataset 5/5, n=26) or withdrawn (dataset 5/3, n=5). Duplicate data in dataset 5/4 has been removed (see below).
3. In previous IntCal curves the Kodiak Island (KI) tree 14C data were corrected for a 14 ± 3 14C yr offset between a tree growing on Kodiak Island, Alaska (dataset 1/1) and Washington state (Stuiver and Braziunas Reference Stuiver and Braziunas1998). However, in IntCal20 the dataset’s scaled deviation and mean offset as estimated during screening (see below) did not flag this as being an outlier. This correction was therefore not applied in IntCal20.
Because of the large amount of new data under consideration, particularly from 0 to 3000 cal BP, a minimum length for datasets was adopted to allow a realistic assessment of their reliability against existing datasets (10 measurements for decadal samples, 15 for 5-ring samples, 20 for 3-ring samples or 100 for single-year data, if not replicated by a second laboratory). An exception to the dataset length requirement was made for short series from laboratories also producing long datasets that passed the screening requirements. Another exception was data from the 14C spike events (Miyake et al. Reference Miyake, Nagaya, Masuda and Nakamura2012, Reference Miyake, Masuda and Nakamura2013) that had been replicated worldwide by numerous laboratories.
Twenty of the new datasets under consideration did not meet these length criteria and have been retained as comparison datasets. An unpublished dataset of three 10-ring samples of Irish oak from 3450–3470 cal BP (measured at the Center for Accelerator Mass Spectrometry, Lawrence Livermore National Laboratory) that was included in IntCal13, was also too short and redundant with all the new single-year measurements in the same time period (e.g. Pearson et al. Reference Pearson, Brewer, Brown, Heaton, Hodgins, Jull, Lange and Salzer2018, Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue).
As a primary screening exercise, a preliminary curve was estimated using all the data under initial consideration. For each 14C constituent dataset the scaled deviation (consisting of the sum of the scaled residuals) and the mean offset from this preliminary curve were calculated. This highlighted data which indicated potential inconsistencies relative to the other datasets and required further consideration. For those datasets with large scaled deviations (as assessed by a p-value) and high mean offsets, the authors were contacted and in most cases indicated there was a problem with the measurements that had not been resolved; hence these data are not included.
After this initial stage of screening, the process was repeated whereby another preliminary curve was created, but without those datasets excluded by the first screening. The p-values for the scaled deviations and mean residuals were re-calculated flagging up datasets that needed further individual consideration by the group. This was performed by visual inspection of plots and discussion within the group ending with a vote on inclusion. Data which were judged to be too scattered were excluded from the curve including Irish oak data published by McCormac et al. (Reference McCormac, Bayliss, Brown, Reimer and Thompson2008; dataset 2/6), which had been included in IntCal09 and IntCal13.
Two further categories of data were excluded from IntCal20: (1) a small number of recent datasets which appeared to be depleted in 14C resulting from the use of fossil fuels during the industrial revolution (Tans et al. Reference Tans, de Jong and Mook1979), and (2) datasets within or at the present day limit of the Inter-tropical Convergence Zone (ITCZ, see below). An inter-laboratory tree-ring dating comparison led by L. Wacker was organized by the IntCal Dendrochronology focus group. The anonymized results of this comparison are presented in Wacker et al. (Reference Wacker, Scott, Bayliss, Brown, Bard, Bollhalder, Friedrich, Capano, Cherkinsky, Chivall, Culleton, Dee, Friedrich, Hodgins, Hogg, Kennett, Knowles, Kuitems, Lange, Miyake, Nadeau, Nakamura, Naysmith, Olsen, Omori, Petchey, Philippsen, Bronk Ramsey, Prasad, Seiler, Southon, Staff and Tuna2020 in this issue) and provide insights into the accuracy and quality of high-precision measurements on single tree rings performed by the participating AMS laboratories. The Holocene measurements obtained by AMS are comparable in quality to the ones previously performed by decay counting (Stuiver et al. Reference Stuiver, Reimer, Bard, Beck, Burr, Hughen, Kromer, McCormac, Van der Plicht and Spurk1998a), though requiring several orders of magnitude less material, whereas during the late glacial (ca. 15–11.7 cal kBP), AMS measurements in IntCal20 are superior to previous decay counting results (Sookdeo et al. Reference Sookdeo, Kromer, Buentgen, Friedrich, Friedrich, Helle, Pauly, Nievergelt, Reinig, Treydte, Synal and Wacker2019 in this issue). As with previous calibration curves, some of the tree-ring datasets included in the curve are more variable than the quoted uncertainties would indicate i.e. 14C determinations arising from tree rings with identical calendar years appear more widely spread than would be supported by their reported uncertainties. We call this additional variability over-dispersion. Rather than include a laboratory error multiplier as was done in the past, an additive error to correct for potential over-dispersion in the IntCal20 measurements was built into the Bayesian statistical method (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). By specifically including such an additive term to model over-dispersion we aimed to correct not only for any potential under-reporting of laboratory measurement error within the IntCal20 datasets but also potential dispersion caused by intra-hemispheric locational offsets and other inter-tree variation. A prior probability distribution (hereafter prior) for the level of over-dispersion was formed based upon inter-lab variability of the same tree-ring samples produced for the Sixth International Radiocarbon Intercomparison (SIRI, Scott et al. Reference Scott, Naysmith and Cook2017b). This prior was expected to be somewhat conservative for the IntCal20 data (i.e. indicate a greater level of over-dispersion) due to the much wider set of AMS laboratories participating in SIRI than used for IntCal20. However, due to the large volume of IntCal20 data, our posterior estimate for the over-dispersion is dominated by the high quality IntCal20 data themselves. The posterior estimate for the over-dispersion within the Northern Hemisphere IntCal20 datasets can be seen in Heaton et al. (Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue, Figure 5). Anticipating similar levels of over-dispersion amongst the 14C determinations users wish to calibrate, to improve calibration accuracy, this posterior is incorporated into our published curve through the creation of predictive intervals.
Consideration of regional and seasonal growth offsets in tree-ring 14C
While 14C offsets between the Southern and Northern Hemispheres are well documented (McCormac et al. Reference McCormac, Hogg, Higham, Lynch, Broecker, Baillie, Palmer, Xiong, Pilcher, Brown and Hoper1998; Stuiver and Braziunas Reference Stuiver and Braziunas1998; Hogg et al. Reference Hogg, Palmer, Boswijk, Reimer and Brown2009; Turney et al. Reference Turney, Palmer, Hogg, Fogwill, Jones, Ramsey, Fenwick, Grierson, Wilmshurst, O’Donnell, Thomas and Lipson2016a), offsets within the Northern Hemisphere are less well understood. Intrahemispheric offsets were predicted by a global tracer transport model using ocean boundary conditions (Braziunas et al. Reference Braziunas, Fung and Stuiver1995) to be on the order of 8 14C yr or less in the Northern Hemisphere except at very high latitudes (>70°N). However, offsets could also result, in theory, from the location of the tree relative to the ITCZ and monsoons, growing season differences, polar latitudes, proximity to upwelling of 14C-depleted ocean water, proximity to industrial centers, and high altitude. Regional offsets within a hemisphere can be difficult to corroborate, as they are of a scale similar to observed inter-laboratory variation (Wacker et al. Reference Wacker, Scott, Bayliss, Brown, Bard, Bollhalder, Friedrich, Capano, Cherkinsky, Chivall, Culleton, Dee, Friedrich, Hodgins, Hogg, Kennett, Knowles, Kuitems, Lange, Miyake, Nadeau, Nakamura, Naysmith, Olsen, Omori, Petchey, Philippsen, Bronk Ramsey, Prasad, Seiler, Southon, Staff and Tuna2020 in this issue; Friedrich et al. Reference Friedrich, Kromer, Wacker, Olsen, Remmele, Lindauer, Land and Pearson2020 in this issue; Pearson et al. Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue) but have been observed convincingly in a few cases (Turney et al. Reference Turney, Palmer, Hogg, Fogwill, Jones, Ramsey, Fenwick, Grierson, Wilmshurst, O’Donnell, Thomas and Lipson2016a; Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018; Pearson et al. Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue).
The ITCZ is an asymmetric area of low pressure around the thermal equator where the northeast and southeast trade winds converge. The ITCZ migrates on seasonal and longer timescales (Haug et al. Reference Haug, Hughen, Sigman, Peterson and Röhl2001; Schneider et al. Reference Schneider, Bischoff and Haug2014). In extreme situations, the ITCZ appears to have experienced a major southward migration across Amazonia during Heinrich stadials (Cheng et al. Reference Cheng, Sinha, Cruz, Wang, Edwards, d’Horta, Ribas, Vuille, Stott and Auler2013). Trees growing within the ITCZ are potentially subjected to air masses from different hemispheres at certain times of the year (Marsh et al. Reference Marsh, Bruno, Fritz, Baker, Capriles and Hastorf2018; Hogg et al. Reference Hogg, Heaton, Hua, Palmer, Turney, Southon, Bayliss, Blackwell, Boswijk, Bronk Ramsey, Pearson, Petchey, Reimer, Reimer and Wacker2020 in this issue). For example, Southern Hemisphere air masses in tropical and subtropical Brazil have been detected in 14C measurements from trees growing in the 1960s (Lisi et al. Reference Lisi, Pessenda, Tomazello and Rozanski2001). Hua et al. (Reference Hua, Barbetti, Zoppi, Fink, Watanasak and Jacobsen2004) similarly concluded that tropical trees from Thailand had lowered 14C levels because of the influence of Southern Hemisphere air masses. The authors reported an offset of 32 ± 8 14C yr for pine from north-central Thailand compared to trees from the northwest United States (Stuiver et al. Reference Stuiver, Reimer and Braziunas1998b) between AD 1690 and 1780. However, this appears to be primarily an inter-laboratory effect, since the Thai data are younger than Tasmanian trees measured concurrently at the same laboratory (Hua et al. Reference Hua, Barbetti, Zoppi, Fink, Watanasak and Jacobsen2004) by 30 ± 8 14C yr for AD 1620–1780 (data presented in Table 1 in Hogg et al. Reference Hogg, Turney, Palmer, Cook and Buckley2013a), which is identical to the interhemispheric offset for the same interval based on New Zealand cedar and British oak of 28–32 ± 7 14C yr (Hogg et al. Reference Hogg, McCormac, Higham, Baillie and Palmer2002).
Tree-ring data from between or near the boundaries of the present day ITCZ (Figure 1) were therefore not included in IntCal20 but retained in the database for comparison. These include measurements from pine trees from Thailand obtained inside the ITCZ (Hua et al. Reference Hua, Barbetti, Zoppi, Fink, Watanasak and Jacobsen2004; Q. Hua, personal communication). In addition, a Tibetan juniper growing at 31ºN 91ºE (Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018), approximately at the northern boundary of the present day ITCZ, was not included because this dataset had a mean difference of 18.5 14C yr older compared to other IntCal datasets, which suggested a moderate influence of Southern Hemisphere air.
While altitude has been postulated as mechanism for increased 14C in tree rings (Cain and Suess Reference Cain and Suess1976), there is no evidence for this in more recent higher precision measurement of high elevation trees compared to low- and mid-elevation trees growing during 14C spike events (Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018). However, altitude is a factor in growing season differences. Northern Hemisphere seasonal differences in 14C between plants growing in the early spring and later in the summer can come about because stratospheric 14C is injected into the troposphere during the boreal spring (Appenzeller et al. Reference Appenzeller, Holton and Rosenlof1996; Stohl et al. Reference Stohl, Bonasoni, Cristofanelli, Collins, Feichter, Frank, Forster, Gerasopoulos, Gäggeler, James, Kentarchos, Kromp-Kolb, Krüger, Land, Meloen, Papayannis, Priller, Seibert, Sprenger, Roelofs, Scheel, Schnabel, Siegmund, Tobler, Trickl, Wernli, Wirth, Zanis and Zerefos2003). For example, Dee et al. (Reference Dee, Brock, Harris, Bronk Ramsey, Shortland, Higham and Rowland2010) reported an offset of 19 ± 5 14C yr between short-lived herbaria specimens collected in Egypt between AD 1700 and 1900 and IntCal09. Other studies using blocked (multiyear) tree-ring data have indicated that differences may be enhanced during periods of low solar activity when 14C production is higher (Kromer et al. Reference Kromer, Manning, Kuniholm, Newton, Spurk and Levin2001). For example, Kromer et al. (Reference Kromer, Manning, Kuniholm, Newton, Spurk and Levin2001) found only a minimal expected latitudinal offset between the 14C ages of Turkish pines and German oak on average from AD 1420 and 1640 but the Turkish pines were older than the German oak by 17 years during the Spörer solar activity minimum. Dellinger et al. (Reference Dellinger, Kutschera, Nicolussi, Schießling, Steier and Wild2004) found deviations of up to 17 ± 5 14C yr for stone pine growing in the Alps between 3500 BC and 3000 BC compared to the low altitude tree-ring measurements that were included in IntCal98. Manning et al. (Reference Manning, Griggs, Lorentzen, Bronk Ramsey, Chivall, Jull and Lange2018) also reported fluctuating regional offsets from AD 1610 to 1940 from trees growing in Jordan compared with IntCal13 averaging 19 ± 3 14C yr, associated with periods of reversals and plateaus in the 14C calibration record. However, this average offset is reduced to less than 10 14C yr when compared to new datasets included in IntCal20 (L. Wacker, personal communication). Comparison of data from Germany and Turkey measured at the same laboratory—removing the issue of inter-laboratory variation as a cause—indicates similar fluctuating offsets in the period from the 17th to the 8th centuries BC that are again associated with reversals and plateaus in the 14C calibration record (Manning et al. Reference Manning, Kromer, Cremaschi, Dee, Friedrich, Griggs and Hadden2020).
While the mentioned examples may overestimate regional offsets, the large influx of annual tree-ring data submitted to IntCal20 offers a range of new approaches to study this issue. The results of a study of the global extent of cosmic events showed only slight differences between trees growing through a range of growth seasons across a range of environments during the years 774 and 993 AD and suggests only a slight latitudinal offset at these times (Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018: Fig. 3). Pearson et al. (Reference Pearson, Brewer, Brown, Heaton, Hodgins, Jull, Lange and Salzer2018) reported Irish oak latewood representing mid-May through early autumn growth (Baillie Reference Baillie1982) and North American bristlecone pine whole tree rings (representing June, July, August growth) which were within stated errors of one another in the period 1700–1500 BC. Pearson et al. (Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue) refine this to an average weighted mean difference of –8.1 ± 1.9 14C yr between Irish and North American 14C data for this period. This is still within stated errors but may also reflect a slight latitudinal effect.
Future work on growing season differences and latitudinal dependences is therefore recommended along with exploration of other factors such as latitude or altitude. Seasonality will be particularly important for tracking and defining any new discoveries of rapid excursions in atmospheric 14C concentration. For example, in the Southern Hemisphere, growth is split across two calendar years and for European oak, the earlywood is formed using photosynthates from the previous calendar year (Pilcher Reference Pilcher1995). Either of these could potentially aid in refining the timing of rapid (intra- and inter-annual) events. In regions north of the polar front, atmospheric 14C may be elevated in late spring/early summer due to stratospheric injection of 14C and therefore could, in theory, enrich the 14C of trees growing north of the polar front. Stuiver and Braziunas (Reference Stuiver and Braziunas1998) found only a minimal Δ14C offset (–0.3 ± 0.7 ‰) for AD 1615–1715 but an offset of 26 ± 6 14C yr younger for AD 1545–1615 for a Siberian larch tree (67°N, 123°E) compared to a tree from Washington state (48°N, 124°W) which is in good agreement with Büntgen et al. (Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018). Data from northern Norway from trees growing during the peak of nuclear weapons testing also had higher 14C (Hua and Barbetti Reference Hua and Barbetti2007; Svarva et al. Reference Svarva, Grootes, Seiler, Stene, Thun, Værnes and Nadeau2019) but may not be representative of natural offsets due to the high latitude of many of the atmospheric bomb tests. Büntgen et al. (Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018) reported elevated 14C values for some trees growing above 60ºN at the peak of the AD 774/5 Miyake event (Miyake et al. Reference Miyake, Nagaya, Masuda and Nakamura2012). The position of the present-day polar jet stream, which delineates the polar front, is presented as a latitudinal probability distribution by Molnos et al. (Reference Molnos, Mamdouh, Petri, Nocke, Weinkauf and Coumou2017), but a simple boundary is not easily established. We therefore used 60ºN for comparison of northerly trees with the other data. We found only small offsets for most tree ring 14C data in the compilation above 60ºN so retained the following datasets for use in the curve: SWE02 (68.3°N, 19.6°E; dataset 69/34), Kom1213175a/b (68.5°N, 20.0°E; dataset 60/4), RUS04 (67.5°N, 70.7°E; dataset 69/42), and Yamal (67.5°N, 70.7°E; dataset 68/8). Büntgen et al. (Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018) reported offsets between 12 ± 6 and 27 ± 5 14C yr younger for samples above 65°N measured at ETH. The potential for a latitudinal offset needs to be considered more carefully in the future.
Proximity to coasts with upwelling of older oceanic carbon has been proposed to cause 14C offsets. As mentioned earlier, Stuiver and Braziunas (Reference Stuiver and Braziunas1998) found a 14 ± 3 14C yr offset between a tree growing on Kodiak Island, Alaska (KI tree; dataset 1/1), and those trees growing in Washington State, USA. 14C offsets between trees from Japan and the IntCal curves for several time periods have also been postulated to be due to ocean upwelling (e.g. Nakamura et al. Reference Nakamura, Miyahara, Masuda, Menjo, Kuwana, Kimura, Okuno, Minami, Oda, Rakowski, Ohta, Ikeda and Niu2007). It is not clear if these latter observations are real or a product of inter-laboratory variation.
To summarize, regional 14C offsets can be difficult to determine due to measurement uncertainties and inter-laboratory offsets. Such analyses, however, are critical for future calibration curves, particularly to define the boundaries and changes through time of the ITCZ as well as growing season effects. 14C measurements of tropical trees would provide much needed information on the ITCZ, however, it can be difficult to obtain reliable dendrochronological dates due to the limited seasonality in the tropics and subsequent indistinct tree rings. Through the application of X-ray densitometry and confirmation through 14C measurements of trees growing during the nuclear weapons testing in the 1960s, chronology establishment was successful for some tropical species (Lisi et al. Reference Lisi, Pessenda, Tomazello and Rozanski2001; Santos et al. Reference Santos, Linares, Lisi and Tomazello Filho2015). This may provide an improved understanding of the offsets because of the higher 14C levels (Hua and Barbetti Reference Hua and Barbetti2007).
Dataset updates
Irish oak data from the Waikato laboratory (Hogg et al. Reference Hogg, Palmer, Boswijk, Reimer and Brown2009) for the intervals AD 245−335, 745−785, and 895–935 had accidentally been left out of IntCal13 and are now included. Decadal German oak data from the Heidelberg laboratory for the period 1600–1700 BC were inadvertently entered twice with different laboratory ID’s in IntCal09 and IntCal13. This problem was corrected for IntCal20.
From IntCal04 through IntCal13 (Reimer et al. Reference Reimer, Baillie, Bard, Bayliss, Beck, Bertrand, Blackwell, Buck, Burr, Cutler, Damon, Edwards, Fairbanks, Friedrich, Guilderson, Hogg, Hughen, Kromer, McCormac, Manning, Bronk Ramsey, Reimer, Remmele, Southon, Stuiver, Talamo, Taylor, van der Plicht and Weyhenmeyer2004, Reference Reimer, Baillie, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Burr, Edwards, Friedrich, Grootes, Guilderson, Hajdas, Heaton, Hogg, Hughen, Kaiser, Kromer, McCormac, Manning, Reimer, Richards, Southon, Talamo, Turney, van der Plicht and Weyhenmeyer2009, Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Cheng, Edwards, Friedrich, Grootes, Guilderson, Haflidason, Hajdas, Hatté, Heaton, Hoffmann, Hogg, Hughen, Kaiser, Kromer, Manning, Niu, Reimer, Richards, Scott, Southon, Staff, Turney and J2013b), laboratory error multipliers for the tree-ring data were calculated from the offset with Seattle (QL) measurements with an estimated 1.3 error multiplier applied. Although no correction was made to the data for the calculated offset as had been done in IntCal98 (Stuiver et al. Reference Stuiver, Reimer, Bard, Beck, Burr, Hughen, Kromer, McCormac, Van der Plicht and Spurk1998a) the error multipliers increased the uncertainty in the data.
The Seattle error multiplier was re-calculated from replicates using equation 2 from Scott et al. (Reference Scott, Naysmith and Cook2017a). Of the replicates, 459 were duplicates, 35 were triplicates and there was 1 set each of quadruplets and quintuplets. The lab error multiplier (k) was calculated to be 1.07. Since the replicates were almost all aliquots of the same wood processed to alpha cellulose it was decided to leave the error multiplier at 1.3 which should encompass any additional variability such as a cellulose processing error. The laboratory error multipliers for the other legacy datasets were also left at the 2004 values with the exception of the more recent data from Belfast and Waikato where intra-laboratory multipliers had already been included in the reported uncertainties (McCormac et al. Reference McCormac, Bayliss, Baillie and Brown2004; Hogg et al. Reference Hogg, Palmer, Boswijk, Reimer and Brown2009; datasets 2/1, 2/2, 3/1 and 3/2). The laboratory error multipliers for these datasets were therefore set to 1 in order not to apply the error multipliers twice.
A revised radon correction was applied to the Seattle data measured from 1977 to 1987 (Stuiver et al. Reference Stuiver, Reimer and Braziunas1998b). As an additional check on the revised radon correction, 10 decadal wood samples from a Douglas fir (S tree; dataset 1/10) from the Seattle laboratory were processed to cellulose by Fusa Miyake and measured by AMS in Belfast. Replicate AMS measurements on the cellulose were made on three samples to check potential outliers. The results of the new S tree cellulose extractions are within one standard deviation from the Seattle radon corrected measurements of the S tree and a sequoia (RC tree) except for one sample at 995 cal BP (Figure S1; Table S1). These new replicate data have not been included in IntCal20.
Same cellulose replicates and processing error estimation
In order to avoid over-precise error estimates from averaging of replicates made on the same cellulose, a correction was made for cellulose processing differences. The cellulose processing error, in terms of Δ14C, was estimated at 1‰ (1 σ; equivalently 8 14C yr) (L. Wacker, personal communication) and may be even less for the large carbon mass samples used for radiometric dates. For replicates, identified by the same laboratory identification number, the cellulose processing uncertainty was removed from the total uncertainty by subtracting 8 14C yr in quadrature. A weighted mean of the 14C ages was calculated with the uncertainty in the mean given by  $\sqrt {{1 \over {\left( {{1 \over {{\sigma _1}^2}}} \right) + \left( {{1 \over {{\sigma _2}^2}}} \right)}}} $ where σ1 and σ2 are the measurement uncertainties in the 14C ages of the replicates. Finally, the cellulose processing error was added in quadrature to the uncertainty in the mean.
$\sqrt {{1 \over {\left( {{1 \over {{\sigma _1}^2}}} \right) + \left( {{1 \over {{\sigma _2}^2}}} \right)}}} $ where σ1 and σ2 are the measurement uncertainties in the 14C ages of the replicates. Finally, the cellulose processing error was added in quadrature to the uncertainty in the mean.
New measurements of single dendrochronologically dated tree rings
Publication of the rapid increase in atmospheric 14C in AD 774–775 (also known as the “Miyake event”) and the subsequently discovered AD 993 event (Miyake et al. Reference Miyake, Masuda and Nakamura2013) has prompted 14C measurements on additional single tree rings from these time periods (e.g. Jull et al. Reference Jull, Panyushkina, Lange, Kukarskih, Myglan, Clark, Salzer, Burr and Leavitt2014; Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018; Kudsk et al. Reference Kudsk, Philippsen, Baittinger, Fogtmann-Schulz, Knudsen, Karoff and Olsen2019 in this issue) and led to the search for additional unusual events that can be detected in annual or biannual measurements (e.g. Miyake et al. Reference Miyake, Jull, Panyushkina, Wacker, Salzer, Baisan, Lange, Cruz, Masuda and Nakamura2017a, Reference Miyake, Masuda, Nakamura, Kimura, Hakozaki, Jull, Lange, Cruz, Panyushkina, Baisan and Salzer2017b; Jull et al. Reference Jull, Panyushkina, Miyake, Masuda, Nakamura, Mitsutani, Lange, Cruz, Baisan and Janovics2018). To incorporate the large amount of annual data that have been produced for several of these short time periods and to represent the rapid increases, additional knots in the spline were included at these points for calibration curve construction (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue).
Dating of the second millennium BC eruption of Thera (Santorini) has long been a contentious issue for Mediterranean archaeology. Bayesian models using the more recent iterations of IntCal have pointed to a late 17th century BC eruption, contrary to some interpretations of the archaeological and historical evidence which indicate a more recent eruption date (Kutschera et al. Reference Kutschera, Bietak, Wild, Bronk Ramsey, Dee, Golser, Kopetzky, Stadler, Steier and Thanheiser2012; Manning et al. Reference Manning, Höflmayer, Moeller, Dee, Bronk Ramsey, Fleitmann, Higham, Kutschera and Wild2014; and references therein). A recent publication of single-year bristlecone pine and Irish oak samples (Pearson et al. Reference Pearson, Brewer, Brown, Heaton, Hodgins, Jull, Lange and Salzer2018) indicated that an annual calibration dataset might offer a new approach to this issue by refining the curve shape. IntCal13 was based on 20-, 10- and 5-ring samples of wood for this period and included a flat region or plateau. The annual calibration dataset has refined the definition of the plateau which is very important for establishing the true possible calendar age ranges for the key Theran datasets. Calibration models using a curve constructed in the same way as IntCal13 from the new bristlecone and oak data increased the probability of a more recent eruption (Pearson et al. Reference Pearson, Brewer, Brown, Heaton, Hodgins, Jull, Lange and Salzer2018). To test these multispecies tree-ring data, a number of laboratories have now analyzed contemporary tree rings at annual resolution (Friedrich et al. Reference Friedrich, Kromer, Wacker, Olsen, Remmele, Lindauer, Land and Pearson2020 in this issue; Kuitems et al. Reference Kuitems, van der Plicht and Jansma2020 in this issue; Pearson et al. Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue). All the new data for this time period that were available at the time of the curve construction have been included in IntCal20. Implications for the dating of the Thera eruption are discussed in light of the IntCal20 curve in Friedrich et al. (Reference Friedrich, Kromer, Wacker, Olsen, Remmele, Lindauer, Land and Pearson2020 in this issue), Pearson et al. (Reference Pearson, Wacker, Bayliss, Brown, Salzer, Brewer, Bollhalder, Boswijk and Hodgins2020 in this issue), Kuitems et al. (Reference Kuitems, van der Plicht and Jansma2020 in this issue), and van der Plicht et al. (Reference van der Plicht, Bronk Ramsey, Heaton, Scott and Talamo2020 in this issue).
The Hallstatt plateau (ca. 800–400 BC), one of the largest flatter regions in the calibration curve, has been problematic for resolving 14C dating chronologies during a critical period in prehistorical technological developments in Europe and elsewhere without adequate stratigraphic control (Hamilton et al. Reference Hamilton, Haselgrove and Gosden2015). Single-ring data from German oak and sequoia now provide detail for the first half of the Hallstatt plateau (2805–2575 cal BP) and increased the dating resolution across this key period (Park et al. Reference Park, Southon, Fahrni, Creasman and Mewaldt2017; Fahrni et al. Reference Fahrni, Southon, Fuller, Park, Friedrich, Muscheler, Wacker and Taylor2020 in this issue).
Annual data for the period 290–486 AD (1660–1464 cal BP) (Friedrich et al. Reference Friedrich, Kromer, Sirocko, Esper, Lindauer, Nievergelt, Heussner and Westphal2019) have also provided improved resolution of the IntCal raw data. These annual datasets demonstrate periodic changes in the annual records which may be attributed to the “11-year” Schwabe cycle (with a length from 9 to 11 years). They also show a ca. 20 14C yr offset from IntCal13 for a part of the time period covered, which is not explained by regional/latitudinal differences but more likely indicates that the curve could be slightly improved by more highly resolved data for a part of this period.
Floating tree-ring sequences: changes and additions
A major inter-comparison exercise using late glacial floating kauri tree-ring sequences (Hogg et al. Reference Hogg, Southon, Turney, Palmer, Bronk Ramsey, Fenwick, Boswijk, Büntgen, Friedrich and Helle2016) resulted in a 14C wiggle-match, with correction for the interhemispheric offset, to the European Preboreal Pine (PPC) chronology (Friedrich et al. Reference Friedrich, Remmele, Kromer, Hofmann, Spurk, Kaiser, Orcel and Küppers2004). This in turn indicated that the Swiss ZHYD-1 (formerly YD-B) record (Schaub et al. Reference Schaub, Kaiser, Frank, Büntgen, Kromer and Talamo2008; Hua et al. Reference Hua, Barbetti, Fink, Kaiser, Friedrich, Kromer, Levchenko, Zoppi, Smith and Bertuch2009; Kaiser et al. Reference Kaiser, Friedrich, Miramont, Kromer, Sgier, Schaub, Boeren, Remmele, Talamo, Guibal and Sivan2012) was incorrectly linked to the PPC. Tree-ring width reanalysis and annual resolution 14C measurements between 13,150 and 11,800 cal BP of previously collected Swiss trees (Kromer et al. Reference Kromer, Friedrich, Hughen, Kaiser, Remmele, Schaub and Talamo2004; Schaub et al. Reference Schaub, Kaiser, Frank, Büntgen, Kromer and Talamo2008; Hua et al. Reference Hua, Barbetti, Fink, Kaiser, Friedrich, Kromer, Levchenko, Zoppi, Smith and Bertuch2009; Kaiser et al. Reference Kaiser, Friedrich, Miramont, Kromer, Sgier, Schaub, Boeren, Remmele, Talamo, Guibal and Sivan2012), as well as the recently discovered additional Swiss subfossil samples (Reinig et al. Reference Reinig, Nievergelt, Esper, Friedrich, Helle, Hellmann, Kromer, Morganti, Pauly, Sookdeo, Tegel, Treydte, Verstege, Wacker and Büntgen2018), enabled the dendrochronological extension of the PPC (Reinig et al. Reference Reinig, Sookdeo, Esper, Friedrich, Guidobaldi, Helle, Kromer, Nievergelt, Pauly, Tegel, Treydte, Wacker and Büntgen2020 in this issue), which is supported by 14C wiggle-matching (Sookdeo et al. Reference Sookdeo, Kromer, Buentgen, Friedrich, Friedrich, Helle, Pauly, Nievergelt, Reinig, Treydte, Synal and Wacker2019 in this issue). The new PPC extension was then used to more securely wiggle-match the floating kauri chronology (Hogg et al. Reference Hogg, Southon, Turney, Palmer, Bronk Ramsey, Fenwick, Boswijk, Büntgen, Friedrich and Helle2016) which in turn was used to reposition ZHYD-1 and the German/Swiss Central European Lateglacial Master Chronology (CELM) record (A. Sookdeo, personal communication) thus extending it to 14,226 ± 4 cal BP. However, the last few decades of this chronology could not be sampled for 14C measurements. This new positioning was reinforced by the inclusion of single-year measurements of subfossil pine trees from the French Alps (Capano et al. Reference Capano, Miramont, Guibal, Kromer, Tuna, Fagault and Bard2018, Reference Capano, Miramont, Shindo, Guibal, Marschal, Kromer, Tuna and Bard2019 in this issue) which strengthen the curve for this period.
Complementing the above, Adolphi et al. (Reference Adolphi, Muscheler, Friedrich, Güttler, Wacker, Talamo and Kromer2017) correlated three floating tree-ring chronologies from Northern Italy to ice core 10Be datasets for the Bølling chronozone (ca. 14,700–14,000 cal BP, equivalent to GI-1eFootnote 1) which indicated that the IntCal13 curve was too smooth in this period. We have incorporated these datasets but matched to the 14C of the rest of the calibration data rather than using the ice core ages to keep the timescales independent (Muscheler et al. Reference Muscheler, Adolphi, Heaton, Bronk Ramsey, Svensson, van der Plicht and Reimer2020 in this issue).
Further back in time, a 2000-yr-long series of bidecadal measurements of a floating kauri tree-ring chronology spanning Heinrich Stadial 3 (ca. 30.6–28.9 cal kBP, equivalent to GS-5) from Finlayson Farm, New Zealand (Turney et al. Reference Turney, Palmer, Bronk Ramsey, Adolphi, Muscheler, Hughen, Staff, Jones, Thomas and Fogwill2016b) were 14C matched to the other calibration datasets by including an interhemispheric offset 43 ± 23 14C yr (Hogg et al. Reference Hogg, Hua, Blackwell, Niu, Buck, Guilderson, Heaton, Palmer, Reimer, Reimer, Turney and Zimmerman2013b). These measurements provide added detail to the curve for HS-3/GS-5. A 1300-yr-long series on consecutive 100-ring samples from trees from Mangawhai Heads, New Zealand (Turney et al. Reference Turney, Fifield, Hogg, Palmer, Hughen, Baillie, Galbraith, Ogden, Lorrey, Tims and Jones2010) was also included and is discussed in Muscheler et al. (Reference Muscheler, Adolphi, Heaton, Bronk Ramsey, Svensson, van der Plicht and Reimer2020 in this issue).
Plant Macrofossils
Plant macrofossils provide another possible sample type for calibration. The four characteristics to be considered in their application are (1) the reservoir from which their carbon originates, (2) the time period covered by their growth, (3) their preservation, and (4) the ability to provide an independent timescale. For atmospheric calibration this implies that the plant macrofossils should be from terrestrial rather than lacustrine or marine plant species and that they should either be from short-lived species or from annual growth of longer-lived species (leaves, needles and small twigs).
The preservation of such material is poor in many contexts but the anoxic conditions in some lake sediments allows for their preservation in a sufficiently good state for identification, and in sufficient density to provide a quasi-continuous record. Fortunately, such anoxic conditions, with minimal bioturbation can also result in annual layers or varves, which may additionally provide a (normally relative) independent timescale.
However, even in ideal circumstances, plant macrofossils do not allow the density of measurements, or the ability to undertake duplicate or high precision analyses that are afforded by tree rings. For this reason, although they do, like wood, provide a very direct measure of carbon in the atmosphere, they are only really useful for calibration in periods where wood is not available, or to provide a long-term record which spans a much longer timescale than any individual tree-ring series can. These considerations, along with the combination of criteria needed to make plant macrofossils a suitable material for 14C calibration, make suitable records very rare and only the Lake Suigetsu varved sediment macrofossil data (Bronk Ramsey et al. Reference Bronk Ramsey, Staff, Bryant, Brock, Kitagawa, van der Plicht, Schlolaut, Marshall, Brauer, Lamb, Payne, Tarasov, Haraguchi, Gotanda, Yonenobu, Yokoyama, Tada and Nakagawa2012) is included in the IntCal20 curve. It is useful because it provides the only quasi-continuous, truly atmospheric record older than ca. 14,190 cal BP, extending to the limit of the technique. This record has been reanalyzed with an extension and revision of the varve counting through to 50 cal kBP (Schlolaut et al. Reference Schlolaut, Staff, Brauer, Lamb, Marshall, Bronk Ramsey and Nakagawa2018). An updated timescale was modeled (Bronk Ramsey et al. Reference Bronk Ramsey, Heaton, Schlolaut, Staff, Bryant, Brauer, Lamb, Marshall and Nakagawa2020 in this issue) using both the new varve chronology and a 14C wiggle-match to the extended Hulu Cave record (Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018).
Speleothems
Speleothems are secondary carbonate mineral deposits formed in caves. Carbon, and hence 14C, in pristine calcite speleothems is derived from a variety of sources with a spectrum of 14C ages. In simplest terms, these are atmosphere, soil gas, soil organic matter and ancient limestone, the last of which is essentially devoid of 14C and contributes to the dead carbon fraction (DCF; for a recent review see Markowska et al. Reference Markowska, Fohlmeister, Treble, Baker, Andersen and Hua2019). The relative contributions of different carbon pools to speleothem calcite (or aragonite) is site-specific and depends on many factors in the karst geochemical setting that respond to changing local climate and vegetation. Controlling factors of DCF include the extent of open or closed system dissolution of the host rock (Hendy Reference Hendy1971), the spectrum of ages of soil organic matter (Fohlmeister et al. Reference Fohlmeister, Kromer and Mangini2011; Noronha et al. Reference Noronha, Johnson, Southon, Hu, Ruan and McCabe-Glynn2015), and influence of non-carbonic acids such as sulfuric acid (Bajo et al. Reference Bajo, Borsato, Drysdale, Hua, Frisia, Zanchetta, Hellstrom and Woodhead2017). Secular DCF variation is expected and numerous studies have indicated abrupt short-term variations related to climate change (e.g. Oster et al. Reference Oster, Montanez, Guilderson, Sharp and Banner2010; Rudzka et al. Reference Rudzka, McDermott, Baldini, Fleitmann, Moreno and Stoll2011; Lechleitner et al. Reference Lechleitner, Baldini, Breitenbach, Fohlmeister, McIntyre, Goswami, Jamieson, van der Voort, Prufer and Marwan2016), but the relative shifts are difficult to predict. To accommodate this, speleothem DCFs were modeled here as independent fluctuations around a constant mean. We placed a prior on the mean DCF for each speleothem based upon the period of speleothem growth that overlaps with tree ring records included in IntCal20 (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). This overlap additionally provided an estimate of the size of the independent fluctuations around this mean over time. During curve construction we further updated these prior mean DCF values to resolve potential offsets between datasets and obtain posterior DCF estimates for each speleothem.
The Hulu Cave H82 speleothem 14C record was utilized in IntCal13 from the end of the tree ring record at 14,153 cal BP to 26,850 cal BP (Southon et al. Reference Southon, Noronha, Cheng, Edwards and Wang2012). Recent 14C and U-Th measurements on the Hulu Cave MSD and MSL speleothems overlap with the earlier measurements and provide new data to 53.9 cal kBP (Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018). These speleothems were formed in a region of the cave underlying a portion of host rock for which the original limestone has been largely replaced with iron oxides (not sandstone as originally reported by Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018). Speleothem DCF is predicted to be low and, most critically, show only minor variation (Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018) because the waters derive most of their dissolved inorganic carbon from soil CO2 and the lower sections of the vadose pathway, dominated by Fe-oxides, and see minimal contribution from deep-seated soil-organic matter derived CO2. δ13C values of these Hulu Cave stalagmites vary by several per mil (Kong et al. Reference Kong, Wang, Wu, Cheng, Edwards and Wang2005). Notably, however, significant shifts in δ13C do not result in resolvable shifts in DCF (Southon et al. Reference Southon, Noronha, Cheng, Edwards and Wang2012). This decoupling can be explained by the fact that of the many well-known processes that control δ13C (Hendy Reference Hendy1971), a significant subset would not be expected to directly affect DCF. The latter includes shifts in overlying vegetation between C3 and C4 biomes, which is indeed invoked by Kong et al. (Reference Kong, Wang, Wu, Cheng, Edwards and Wang2005) to explain the δ13C variations observed at Hulu. In addition, the lack of nuclear weapons testing 14C in the cave dripwaters, as well as observed seasonal δ18O values, support a relatively short residence time of the soil carbon and infiltration into the cave (Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018).
Each Hulu Cave speleothem was permitted to have a potentially different DCF for the purposes of curve construction. A mean DCF value of 480 ± 8 14C yr was used as a prior for each, with a further independent variation around this mean value in any particular calendar year of ±50 14C yr, based upon calculations from the overlap of H82 with the updated tree ring section of the IntCal20 curves. The slight difference from the DCF value, in any calendar year, of 450 ± 70 14C yr used by Cheng et al. (Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018) is due to improvements in the tree-ring chronologies and additional measurements discussed above. During curve construction, these DCF priors were updated and we obtained posterior DCF estimates of 472 ± 50 14C yr for H82, 470 ± 50 14C yr for MSD, and 481 ± 50 14C yr for MSL respectivelyFootnote 2. This demonstrates the DCF consistency across the three Hulu speleothems.
In addition, we utilize Bahamas speleothems which are represented in IntCal20 by two stalagmites collected in an underwater cave on Grand Bahama; GB89-24-1 (Beck et al. Reference Beck, Richards, Edwards, Silverman, Smar, Donahue, Herrera-Osterheld, Burr, Calsoyas, Jull and Biddulph2001) and GB89-25-3 (Hoffmann et al. Reference Hoffmann, Beck, Richards, Smart, Singarayer, Ketchmark and Hawkesworth2010). The data from these speleothems were incorporated into IntCal13. GB89-25-3 was found broken with 4 basal pieces and 2 top pieces with an intermediate section being lost. Both samples exhibit growth that overlaps with tree ring sections to determine offset and uncertainty. Variation in DCF is greater than that observed in the Hulu speleothem H82. For GB89-24-1, the prior on the mean DCF value was 1515 ± 32 14C yr, with an assumption of additional independent variation around this mean in any calendar year of ±207 14C yr. This prior was updated during curve construction to provide a posterior DCF estimate for GB89-24-1 of 1523 ± 208 14C yr. GB89-25-3 was treated as two separate sections. The prior for the mean DCF of the top sections was set at 2156 ± 33 14C yr, with additional independent variation in any year of ±319 14C yr, based on overlap with tree ring sections. After curve construction, the posterior DCF for these top sections was estimated to be 2173 ± 320 14C yr. For the basal sections an uninformative prior on the mean DCF value was used allowing us to retain internal structure seen within this lower section but allow for a potential step change in DCF from the top sections. After curve construction, we obtained a posterior DCF for these basal section of 2891 ± 323 14C yr (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). The large DCF uncertainties downweight the contribution of the Bahama speleothem records to the calibration curve. However, their inclusion is justified because the agreement between two speleothem records (e.g. Hulu Cave and Bahamas) with very different locations and depositional contexts builds increased confidence in both records as discussed in Southon et al. (Reference Southon, Noronha, Cheng, Edwards and Wang2012).
Marine 14C Archives and Considerations
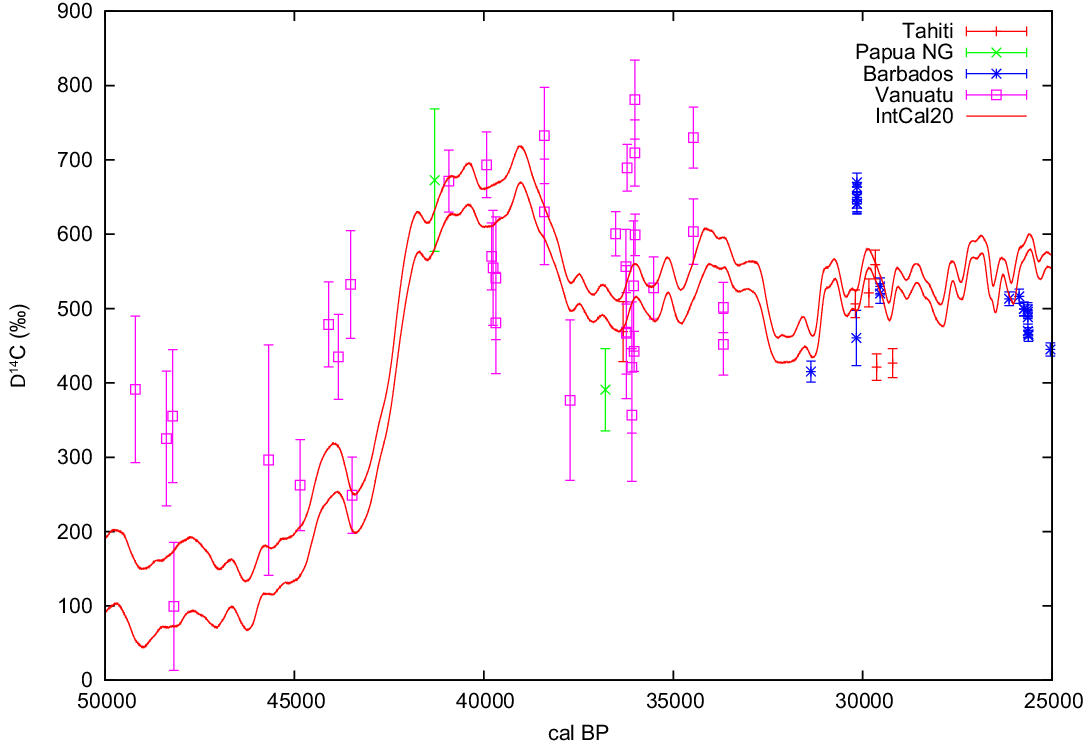
There are no new U-Th dated coral 14C measurements available prior to the Holocene since the publication of the IntCal13 and Marine13 curves (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Cheng, Edwards, Friedrich, Grootes, Guilderson, Haflidason, Hajdas, Hatté, Heaton, Hoffmann, Hogg, Hughen, Kaiser, Kromer, Manning, Niu, Reimer, Richards, Scott, Southon, Staff, Turney and J2013b). However, despite adhering to the IntCal criteria (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Brown, Buck, Edwards and Friedrich2013a), some of the coral data used in IntCal13 exhibit wide scatter in Δ14C (~500 ‰), especially around 37 kyr BP (Figure 2). It is likely that diagenesis due to exposure to freshwater occurred when these corals were above sea level during the lowstand of the Last Glacial Maximum (LGM; 21 ± 2 cal kBP). This effect appears to have been particularly prevalent in corals from areas with rapid uplift such as Vanuatu for which coral Δ14C appears very elevated (>1100‰ around 27–29 cal kBP; Cutler et al. Reference Cutler, Gray, Burr, Edwards, Taylor, Cabioch, Beck, Cheng and Moore2004). In addition, a coral data point from Tahiti at 31 cal kBP is obviously an outlier as presented and discussed in Durand et al. (Reference Durand, Deschamps, Bard, Hamelin, Camoin, Thomas, Henderson, Yokoyama and Matsuzaki2013). It was therefore decided to remove all coral data older than 25 cal kBP for construction of the IntCal20 curves to avoid the potential inclusion of erroneous data. Further work is needed to develop a way of identifying which corals are affected by diagenesis.
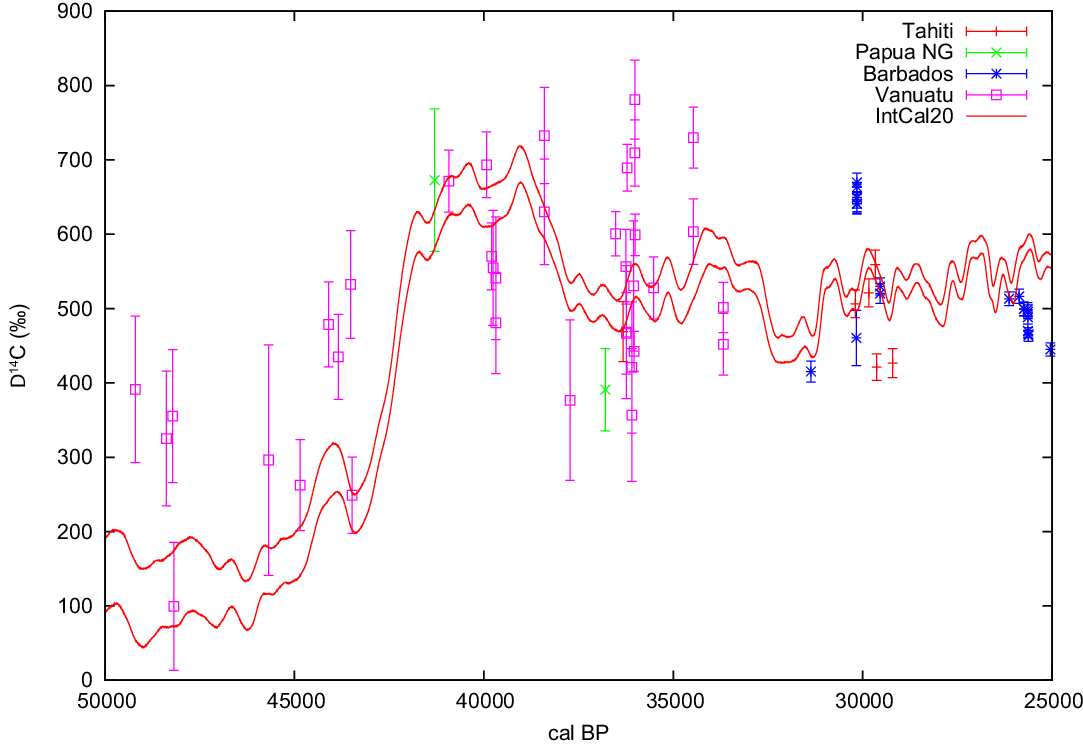
Figure 2 Age-corrected coral Δ14C older than 25 cal kBP from Bard et al. (Reference Bard, Hamelin and Fairbanks1990, Reference Bard, Arnold, Hamelin, Tisnerat-Laborde and Cabioch1998, Reference Bard, Rostek and Ménot-Combes2004a) and Durand et al. (Reference Durand, Deschamps, Bard, Hamelin, Camoin, Thomas, Henderson, Yokoyama and Matsuzaki2013) (Tahiti, Barbados, New Guinea), Cutler et al. (Reference Cutler, Gray, Burr, Edwards, Taylor, Cabioch, Beck, Cheng and Moore2004) (Vanuatu, Papua New Guinea) and Fairbanks et al. (Reference Fairbanks, Mortlock, Chiu, Cao, Kaplan, Guilderson, Fairbanks, Bloom, Grootes and Nadeau2005) (Vanuatu, Barbados) compared to IntCal20 (shown with 1-σ uncertainty envelope). The coral data is not reservoir corrected but this is not relevant for illustrating the large variation in the coral data.
As in IntCal13, the timescales for the marine foraminifera records from the Iberian margin, Pakistan margin and the Cariaco Basin were based on tie-pointing the rapid transitions between stadial and interstadial events in the proxy climate records, assumed to be synchronous within an uncertainty of ±100 yr, to those in the Hulu Cave δ18O values (Wang et al. Reference Wang, Cheng, Edwards, An, Wu, Shen and Dorale2001; Cheng et al. Reference Cheng, Edwards, Sinha, Spötl, Yi, Chen, Kelly, Kathayat, Wang and Li2016) using a Gaussian process model (Heaton et al. Reference Heaton, Bard and Hughen2013). The assumption of synchronicity builds on our previous work focused on a few selected marine sites (see Hughen et al. Reference Hughen, Overpeck, Peterson and Trumbore1996, Reference Hughen, Eglinton, Xu and Makou2004a, Reference Hughen, Southon, Bertrand, Frantz and Zermeno2004b, Reference Hughen, Southon, Lehman, Bertrand and Turnbull2006 for the Cariaco Basin; Bard et al. 2004a, 2004b for the Iberian Margin; and Bard et al. Reference Bard, Ménot, Rostek, Licari, Böning, Edwards, Cheng, Wang and Heaton2013 for the Pakistan Margin) and is supported by modeling results (e.g. Rind et al. Reference Rind, Peteet, Broecker, McIntyre and Ruddiman1986; Manabe and Stouffer Reference Manabe and Stouffer1995) showing tropical Atlantic and Asian responses to North Atlantic cooling, which suggests temporally rapid and spatially coherent changes across the area including the various climate archives.
For the sediment cores from the Pakistan and Iberian margins, the climate proxy records are the same as those described for IntCal13 (Bard et al. Reference Bard, Ménot, Rostek, Licari, Böning, Edwards, Cheng, Wang and Heaton2013). The only significant difference is that the Iberian alkenone-SST record has been remeasured to increase its time resolution and precision (Darfeuil et al. Reference Darfeuil, Ménot, Giraud, Rostek, Tachikawa, Garcia and Bard2016), providing improved confidence in the correlation tie-points. In addition, the 14C chronology of the Pakistan Margin record has been verified by analyzing different planktonic species of foraminifera (Fagault et al. Reference Fagault, Tuna, Rostek and Bard2019). A revision of the Cariaco Basin record tie-pointing and age-depth model has resulted in changes to the timescale used in IntCal13. The depth scale has been corrected as described in Hughen and Heaton (Reference Hughen and Heaton2020 in this issue) and the timescale recalculated.
Marine 14C Reservoir Ages
Marine reservoir age (MRA) changes over time have long been recognized (e.g. Monge Soares Reference Monge Soares1993; Bard et al. Reference Bard, Arnold, Mangerud, Paterne, Labeyrie, Duprat, Melieres, Sonstegaard and Duplessy1994; Austin et al. Reference Austin, Bard, Hunt, Kroon and Peacock1995; Ingram Reference Ingram1998; Voelker et al. Reference Voelker, Sarnthein, Grootes, Erlenkeuser, Laj, Mazaud, Nadeau and Schleicher1998) but have been difficult to quantify for many regions due to the lack of records with independent timescales. In previous versions of IntCal curves, site-specific MRA corrections were applied but these were assumed as constant through time, despite the knowledge that this was an overly simplistic approximation only. For example, it was well recognized that the atmospheric pCO2 minima during the LGM preserved in bubbles from Antarctic ice cores certainly contributed to an MRA increase of about 200 14C yr due to reduced atmospheric CO2 exchange with the ocean (Bard Reference Bard1988; Galbraith et al. Reference Galbraith, Kwon, Bianchi, Hain and Sarmiento2015). Changes in ocean circulation, such as the slowdown of the meridional overturning circulation during the last glacial (ca. 55–15 cal kBP) were likely responsible for additional increases in MRA (e.g. Stern and Lisiecki Reference Stern and Lisiecki2013; Skinner et al. Reference Skinner, Primeau, Freeman, de la Fuente, Goodwin, Gottschalk, Huang, McCave, Noble and Scrivner2017). For previous IntCal iterations, simple error multipliers for marine data were used partly to cover the possible time variations of the reservoir ages.
For IntCal20 it was decided to apply MRA corrections that vary both spatially and temporally. We use MRA fields calculated by means of an enhanced version of the Hamburg Large Scale Geostrophic Ocean General Circulation Model (LSG OGCM) (see Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue, and further references therein) driven by a preliminary atmospheric Δ14C reconstruction based on the Hulu Cave data alone. This preliminary atmospheric, Hulu-Cave-based, Δ14C estimate was obtained with the same Bayesian spline procedure used for IntCal20. Three scenarios of the LSG OGCM model were calculated using climatic boundary conditions, which were originally derived for the present day (PD) and the LGM (scenarios GS and CS). As described by Butzin et al. (Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue), the three scenarios aim at representing the effects of past ocean-climate variability on marine reservoir ages. Scenario PD approximates the Holocene and is also considered as a surrogate for interstadials. Scenario CS results in thermohaline ocean circulation properties characteristic of cold stadials (Sarnthein et al. Reference Sarnthein, Winn, Jung, Duplessy, Labeyrie, Erlenkeuser and Ganssen1994). The GS scenario was chosen for the data correction because it can be considered as an approximation of the average climatic background conditions between 15 and 55 cal kBP.
We obtained, under this GS scenario, Hulu-Cave-based MRA estimates for the LSG OGCM open-ocean site closest to the location of each marine dataset (Figure 3). These MRA estimates were expected to lack some fine scale features, as the Hulu-Cave-based Δ14C reconstruction is somewhat smoothed, yet still provide reliable first-order approximations. Since the IntCal20 marine data come from coastal, rather than open-ocean, sites we adjusted the corresponding nearest open-ocean LSG OGCM estimate by application of a constant coastal shift to obtain dataset-specific priors on the MRA for each marine dataset used in IntCal20. This shift aimed to correct for potential coastal effects not accounted for in the LSG OGCM model. Furthermore, to account for the overly smooth nature of these first-order Hulu-Cave-based MRA estimates we allowed additional independent fluctuations around these shifted estimates. Such an approach is analogous to that used to model the speleothem DCFs but, rather than assuming a constant mean, here we use the coastally shifted shape of the LSG OGCM estimates.
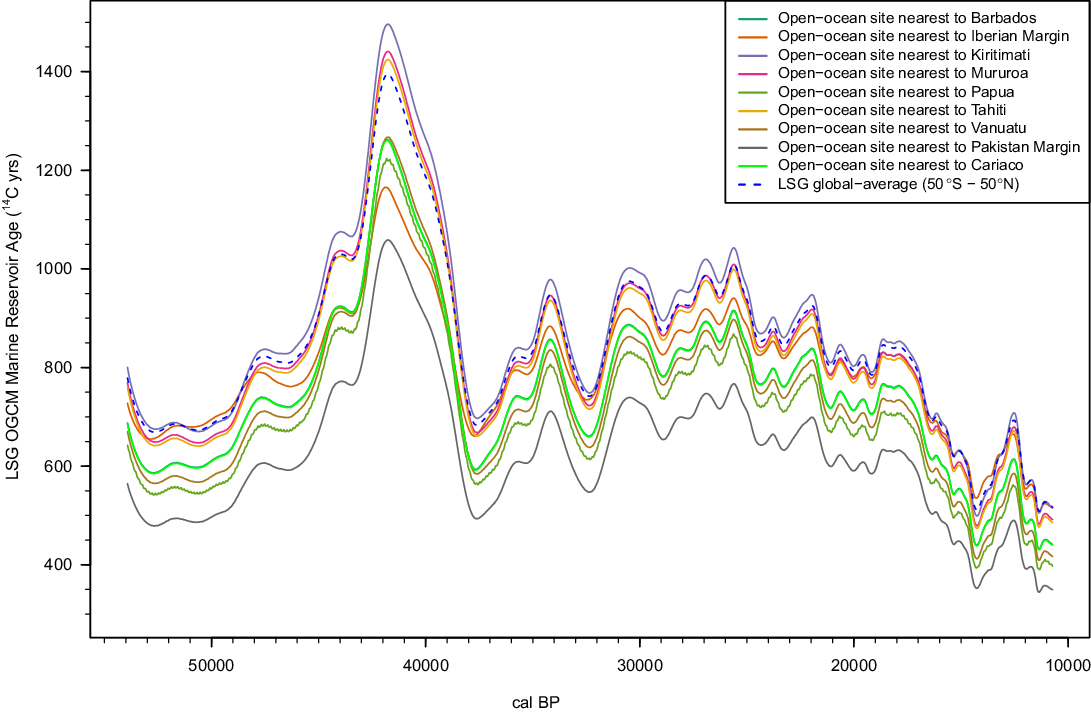
Figure 3 First-order regional open-ocean LSG OGCM MRA estimates based upon the LSG’s Glacial Scenario (Butzin et al. Reference Butzin, Köhler and Lohmann2017, Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue) driven by a preliminary estimate of atmospheric Δ14C obtained from the Hulu cave speleothems alone. The plotted values correspond to the LSG site nearest the location of the marine IntCal20 datasets, the MRAs at the open-ocean sites nearest Barbados and Cariaco have almost indistinguishable plotted values. After application of a constant coastal adjustment, these MRAs are used as priors for the marine data in the creation of IntCal20. Note these Hulu-based estimates are intended solely to aid IntCal20 curve construction. In using Hulu Cave to force the LSG, we aim to provide a first-order approximation to the true regional MRAs which, after permitting some further MRA variability, enable the marine data to contribute to the IntCal20 curve. The plotted values are therefore only preliminary coarse approximations of the MRAs for the relevant locations and lack fine-scale structure.
Equivalent to the speleothem DCFs, for each of the marine IntCal20 datasets, priors on the magnitude of the coastal shift needed and the size of the independent fluctuations around the Hulu-Cave-based first-order estimates were obtained from the observed 14C offset between more recent marine samples from that location and overlapping IntCal20 Northern Hemisphere tree-ring data back to ca. 14,190 cal BP. See Heaton et al. (Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue) for further details and an illustration for Kiritimati. Our prior on the size of coastal shift needed from the open-ocean LSG OGCM estimates ranged from 12 14C yr for Vanuatu corals up to 281 14C yr for Kiritimati. For marine datasets for which we had no observations that overlapped with the Northern Hemisphere tree-ring data, the prior on the coastal shift was chosen to be non-informative while the estimate for the allowable fluctuations was taken from those for sites in the same oceanic region. This non-informative approach permitted us to retain the internal structure in these datasets. With the exception of the Cariaco basin, the resultant coastally shifted prior MRA estimates for each marine dataset were used as inputs for our Bayesian spline method of curve construction. During this process, again analogously to the approach taken to model speleothem DCFs, the constant coastal shift was further updated to resolve potential differences between datasets.
The estimated MRA using the above LSG OGCM based approach was, however, seen to be too high for Cariaco Basin data during the Younger Dryas (ca. 12.9–11.7 cal kBP) which corresponds to Greenland Stadial (GS-1), where it is known to be close to zero from the overlap with the tree rings, and likewise during Heinrich Stadial 1 (ca. 23–12.9 cal kBP, equivalent to GS-2) from comparison with the Hulu Cave data (Hughen and Heaton Reference Hughen and Heaton2020 in this issue). The lack of fit of the LSG OGCM to Cariaco Basin MRA is not surprising given the model resolution of ~380 km compared to the basin size of 160 km by 60 km (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue) and the shallow sill depth (146 m at present) of the basin (Peterson et al. Reference Peterson, Haug, Hughen and Röhl2000). Instead, the MRA for Cariaco Basin was modeled as a slowly varying spline and estimated simultaneously to curve construction. Intuitively, this approach enabled the Cariaco data to offer support to the other IntCal20 datasets whereby 14C variations seen in Cariaco data alone were likely to be assigned as MRA changes within the Cariaco basin and not propagate through to the final Intcal20 curve; while 14C features seen not just in Cariaco but also other records would be more likely retained as genuine atmospheric signal (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). In IntCal09, the Cariaco Basin data for the Younger Dryas/GS-1 were excluded from consideration because the application of a constant marine reservoir offset caused an offset with the other data and likewise during HS-1/GS-2 in IntCal13 (Reimer et al. Reference Reimer, Baillie, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Burr, Edwards, Friedrich, Grootes, Guilderson, Hajdas, Heaton, Hogg, Hughen, Kaiser, Kromer, McCormac, Manning, Reimer, Richards, Southon, Talamo, Turney, van der Plicht and Weyhenmeyer2009, Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Cheng, Edwards, Friedrich, Grootes, Guilderson, Haflidason, Hajdas, Hatté, Heaton, Hoffmann, Hogg, Hughen, Kaiser, Kromer, Manning, Niu, Reimer, Richards, Scott, Southon, Staff, Turney and J2013b). With the modeled spline MRA and updated calendar age timescale for the non-varved record, the Cariaco Basin data from the Younger Dryas/GS-1 and HS-1/GS-2 are no longer offset from the rest of the data and are included in IntCal20. The climatic implications of the modeled reservoir age changes for Cariaco Basin data are discussed in Hughen and Heaton (Reference Hughen and Heaton2020 in this issue). It should also be noted that the modeled spline MRA for Cariaco Basin beyond the end of the Hulu Cave dataset was extrapolated to 55,000 cal BP to provide the final 1030 cal yr of the IntCal20 curve.
CURVE CONSTRUCTION
After the publication of IntCal13, the IWG determined the necessity of a statistically robust calibration curve construction method that could be run much more quickly than the Random Walk Model (Niu et al. Reference Niu, Heaton, Blackwell and Buck2013), so that different data options could be tested. Several Bayesian and frequentist methods (Kernel density, SIMEX, Bayesian spline) were examined by the IntCal statistics focus group who decided upon a Bayesian spline incorporating calendar age uncertainty (Berry et al. Reference Berry, Carroll and Ruppert2002; Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). The quality of fit of the spline to the observed samples is based directly on 14C determinations, while its smoothness is measured in the Δ14C domain. The Bayesian spline method has been refined in a number of ways that are specific to this application, for example to include an additive error term on the 14C determinations to account for potential over-dispersion in observed 14C, to allow for the possibility of heavier-tailed errors on older data, and to explicitly recognise events involving rapid change in atmospheric 14C (e.g. Miyake et al. Reference Miyake, Nagaya, Masuda and Nakamura2012) in the structure of the curve (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue).
RESULTS
Based on tree rings, IntCal20 extends to ca. 13,910 cal BP as a fully atmospheric record. The older part of IntCal20 comprises statistically integrated evidence from floating tree-ring chronologies, lacustrine and marine sediments, speleothems, and corals, using improved evaluation of the time and location variable 14C offsets from the atmosphere (reservoir age, dead carbon fraction) for each dataset back to ca. 53,970 cal BP with MRA corrected Cariaco Basin data providing an extension to 55,000 cal BP. The IntCal20 calibration curve plotted with 1 standard deviation predictive envelopes over the full range of the calibration interval (0–55 cal kBP) in 2000-year intervals with all the datasets and uncertainties is provided in online Supplemental Material (Figure S2). These predictive intervals, and corresponding predictive uncertainties, incorporate the potential for over-dispersion in a future NH atmospheric 14C tree-ring measurement to be calibrated against the curve, i.e. that it too may be subject to some elements of additional intra-hemispheric variation beyond its quoted laboratory uncertainty. In incorporating this predictive element into the uncertainties on the final curve, it becomes more relevant for calibration users (Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue). The entire IntCal20 curve on a calendar grid providing both pointwise means and these predictive uncertainties is available to download at http://intcal.org. IntCal20 contains significantly more fine structure prior to 33 cal kBP than the analogous portion of the IntCal13 curve. This is due to the increase in high resolution data and the improved statistical methods utilized and therefore should be more suitable for wiggle-matching than IntCal13 (Figure S3). The older portion of the IntCal20 curve also has a larger range in Δ14C, with higher values than the highest IntCal13 values and lower values than the lowest IntCal13 values. The IntCal20 curve generally records higher Δ14C than IntCal13 between 33 and 42 cal kBP and lower Δ14C for times prior to 42 cal kBP (Figure 5).
DISCUSSION
A comparison of the IntCal20 and IntCal13 curves without the underlying data for clarity is given in Supplemental Material (Figure S3). Some of the main differences are described in more detail below.
Rapid Excursions in Atmospheric 14C in IntCal20
A number of rapid increases in 14C have recently been identified in annual data from calendar dated tree ring records. The AD 774–775 (1175–1176 cal BP) (Miyake et al. Reference Miyake, Nagaya, Masuda and Nakamura2012) event is the most rapid and largest yet observed and is widely replicated (e.g. Büntgen et al. Reference Büntgen, Wacker, Galván, Arnold, Arseneault, Baillie, Beer, Bernabei, Bleicher, Boswijk, Bräuning, Carrer, Ljungqvist, Cherubini, Christl, Christie, Clark, Cook, D’Arrigo, Davi, Eggertsson, Esper, Fowler, Gedalof, Gennaretti, Grießinger, Grissino-Mayer, Grudd, Gunnarson, Hantemirov, Herzig, Hessl, Heussner, Jull, Kukarskih, Kirdyanov, Kolář, Krusic, Kyncl, Lara, LeQuesne, Linderholm, Loader, Luckman, Miyake, Myglan, Nicolussi, Oppenheimer, Palmer, Panyushkina, Pederson, Rybníček, Schweingruber, Seim, Sigl, Sidorova, Speer, Synal, Tegel, Treydte, Villalba, Wiles, Wilson, Winship, Wunder, Yang and Young2018) and is now considered to have been caused by an extreme solar proton event (Mekhaldi et al. Reference Mekhaldi, Muscheler, Adolphi, Aldahan, Beer, McConnell, Possnert, Sigl, Svensson and Synal2015; Miyake et al. Reference Miyake, Suzuki, Masuda, Horiuchi, Motoyama, Matsuzaki, Motizuki, Takahashi and Nakai2015). A second smaller event has been reported from AD 993 (957 cal BP) (Miyake et al. Reference Miyake, Masuda and Nakamura2013) along with a number of other rapid 14C increases of various scales and possible causes (e.g. Miyake et al. Reference Miyake, Jull, Panyushkina, Wacker, Salzer, Baisan, Lange, Cruz, Masuda and Nakamura2017a, Reference Miyake, Masuda, Nakamura, Kimura, Hakozaki, Jull, Lange, Cruz, Panyushkina, Baisan and Salzer2017b; Jull et al. Reference Jull, Panyushkina, Miyake, Masuda, Nakamura, Mitsutani, Lange, Cruz, Baisan and Janovics2018; O’Hare et al. Reference O’Hare, Mekhaldi, Adolphi, Raisbeck, Aldahan, Anderberg, Beer, Christl, Fahrni and Synal2019). The AD 774–775 event is prominent in IntCal20 although the decline in 14C age is smoothed out due to the time it takes for 14C to mix into the ocean (Figure 4a). This rapid 14C increase will be particularly valuable for precise wiggle-matching sequences of 14C ages (Wacker et al. Reference Wacker, Guttler, Goll, Hurni, Synal and Walti2014) to within 1-yr accuracy across this period. The other events discovered so far are less significant and consequently can only be used for precision wiggle-matching when the highest precision measurements are performed. Nevertheless, these structures revealed by tree ring annual 14C are opening up a wide new range of potential for the synchronization of ice-core and tree-ring records and present new prospects and possibilities for precision dating.
Figure 4 IntCal20 envelope (1 σ) with data included for regions with large differences from IntCal13: (a) AD 774/5 Miyake event, (b) 1500–2000 cal BP, (c) 11,000–15,000 cal BP, and (d) 24.2–22.6 kcal BP. Data are shown with 1-σ errors.
The Hallstatt Plateau
At the beginning of the Hallstatt 14C plateau just after 2700 cal BP, the IntCal20 curve has a sharper dip in 14C age than IntCal13 followed by a sharper rise and fall again around 2600 cal BP (Figure S3). For the rest of the period the curve is generally similar to IntCal13 but with slightly more structure. The additional structure in the curve enhances the potential for wiggle-match dating through the Hallstatt plateau which should be particularly valuable for archaeological studies.
2nd Millennium BP
Larger differences to IntCal13 are seen between 2000–1700 cal BP (Figure 4b). These changes are due to the inclusion of measurements of Japanese tree rings; however immediately before and after this period, the Japanese tree rings are in agreement with European oaks and trees from the west coast of North America. These differences may be due to regional changes in the climate-carbon cycle that have not yet been identified.
Late Glacial
In the late glacial there is a shift to older calendar ages around 12.5 cal kBP, primarily due to the new positioning of the tree ring crosslinks. The IntCal20 curve has more pronounced variations (wiggles) than IntCal13 because of the large amount of single-year data during this period. Floating tree-ring chronologies from Northern Italy provide structure to the curve for the Bølling (GI-1e) including a large trough around 14.8 cal kBP (Figure 4c). The 14C trough appears slightly earlier than the abrupt rise in atmospheric CO2 at the start of Greenland Interstadial 1 that started around 14.6 cal kBP in the highly resolved West Antarctic Ice Sheet Divide ice core on its most recent age scale WD2014 (Marcott et al. Reference Marcott, Bauska, Buizert, Steig, Rosen, Cuffey, Fudge, Severinghaus, Ahn and Kalk2014; Bauska et al. Reference Bauska, Baggenstos, Brook, Mix, Marcott, Petrenko, Schaefer, Severinghaus and Lee2016; Sigl et al. Reference Sigl, Fudge, Winstrup, Cole-Dai, Ferris, McConnell, Taylor, Welten, Woodruff, Adolphi, Bisiaux, Brook, Buizert, Caffee, Dunbar, Edwards, Geng, Iverson, Koffman, Layman, Maselli, McGwire, Muscheler, Nishiizumi, Pasteris, Rhodes and Sowers2016). Such pronounced variations in the calibration curve will result in wide calibration age ranges for single 14C dates from this period as shown in Adolphi et al. (Reference Adolphi, Muscheler, Friedrich, Güttler, Wacker, Talamo and Kromer2017). There is also a pronounced wiggle around 23.6 cal kBP, which is seen in many of the datasets (Figure 4d).
Last Glacial
There are many differences through the last glacial period to the end of the IntCal13 curve at 50 cal kBP with IntCal20 continuing to 55 cal kBP but with a wide error envelope. The changes beyond 30 cal kBP can be best observed in age-corrected Δ14C (Figure 5). In general, IntCal20 Δ14C is higher than IntCal13 from ca. 34–42 cal kBP and lower prior to this.
Figure 5 a) Hulu Cave δ18O (in gray, Cheng et al. Reference Cheng, Edwards, Sinha, Spötl, Yi, Chen, Kelly, Kathayat, Wang and Li2016); NGRIP δ18O (in black, North Greenland Ice Core Project members 2004) with GICC05 timescale multiplied by 1.0063 as a first order correction to the offset between GICC05 and the West Antarctic Ice sheet (WAIS) Divide WD2014 chronology making it compatible with the Hulu Cave δ18O records (Buizert et al. Reference Buizert, Cuffey, Severinghaus, Baggenstos, Fudge, Steig, Markle, Winstrup, Rhodes and Brook2015), b) GlOPIS-75 paleomagnetic stack (Laj et al. Reference Laj, Guillou and Kissel2014; Laj and Kissel Reference Laj and Kissel2015), c) 10Be flux (Muscheler et al. Reference Muscheler, Beer, Kubik and Synal2005). a–c on GICC05 timescale (Svensson et al. Reference Svensson, Andersen, Bigler, Clausen, Dahl-Jensen, Davies, Johnsen, Muscheler, Parrenin, Rasmussen, Roethlisberger, Seierstad, Steffensen and Vinther2008) adjusted to 0 BP = 1950 AD, and d) IntCal20 (red) with IntCal13 (purple) as one sigma envelopes and the average for the Campagnian Ignimbrite (blue point, Giaccio et al. Reference Giaccio, Hajdas, Isaia, Deino and Nomade2017). The duration of the Laschamps event is shown as an open box with the main phase shown as solid red (Lascu et al. Reference Lascu, Feinberg, Dorale, Cheng and Edwards2016). Heinrich Stadials are shown in vertical bands with the timing and duration for H1, H3 and H4 taken from Waelbroeck et al. (Reference Waelbroeck, Lougheed, Vazquez Riveiros, Missiaen, Pedro, Dokken, Hajdas, Wacker, Abbott, Dumoulin, Thil, Eynaud, Rossignol, Fersi, Albuquerque, Arz, Austin, Came, Carlson, Collins, Dennielou, Desprat, Dickson, Elliot, Farmer, Giraudeau, Gottschalk, Henderiks, Hughen, Jung, Knutz, Lebreiro, Lund, Lynch-Stieglitz, Malaizé, Marchitto, Martínez-Méndez, Mollenhauer, Naughton, Nave, Nürnberg, Oppo, Peck, Peeters, Penaud, Portilho-Ramos, Repschläger, Roberts, Rühlemann, Salgueiro, Sanchez Goni, Schönfeld, Scussolini, Skinner, Skonieczny, Thornalley, Toucanne, Rooij, Vidal, Voelker, Wary, Weldeab and Ziegler2019) and references therein and that of H2 (H2a + H2b) from the total organic carbon in Pakistan margin linked to the Hulu Cave timescale (Bard et al. Reference Bard, Ménot, Rostek, Licari, Böning, Edwards, Cheng, Wang and Heaton2013).
The IntCal20 Δ14C curve (Figure 5) concurs better with the amplitude of changes in the paleomagnetic and 10Be records than IntCal13 (Laj et al. Reference Laj, Guillou and Kissel2014; Laj and Kissel Reference Laj and Kissel2015; Muscheler et al. Reference Muscheler, Adolphi, Heaton, Bronk Ramsey, Svensson, van der Plicht and Reimer2020 in this issue) and also agrees well with the independently dated Campagnian Ignimbrite (Giaccio et al. Reference Giaccio, Hajdas, Isaia, Deino and Nomade2017). The rise in Δ14C in IntCal20 is coincident within dating uncertainties with the beginning of the Laschamp geomagnetic excursion as recorded in a Missouri stalagmite (Lascu et al. Reference Lascu, Feinberg, Dorale, Cheng and Edwards2016). The highest Δ14C values in IntCal20 also correspond within dating uncertainties to the timing of the main phase of the Laschamp Event at 41.10 ± 0.35 ka BP (Lascu et al. Reference Lascu, Feinberg, Dorale, Cheng and Edwards2016) which is within 1σ of the timing of the event in GLOPIS (Laj et al. Reference Laj, Guillou and Kissel2014). These high values, however, continue on beyond the end of the Laschamp Event, likely, in part because of the long residence time (>1000 years) of carbon in the deep ocean and in part because of carbon cycle perturbations associated with Heinrich Stadial 4 (ca. 39.9–38.2 cal kBP, equivalent to GS-9), which postdate the Laschamp Event (Cheng et al. Reference Cheng, Edwards, Southon, Matsumoto, Feinberg, Sinha, Zhou, Li, Li and Xu2018). Small but resolvable peaks, which could correlate with the Mono Lake event, are evident in both IntCal20 and IntCal13.
The higher Δ14C values in IntCal20 from ca. 34–42 cal kBP means that the ages calibrated with IntCal20 may be up to 700 years older than with IntCal13 whereas from 42–50 cal kBP the calibrated ages maybe more than 1000 years younger (Figure S3). The maximum 14C age that can be calibrated with IntCal20 is 50,100 BP compared to 46,400 BP for IntCal13.
CONCLUSIONS
In summary, the main advances in the IntCal20 calibration curve are:
1. The inclusion of single-year tree-ring data for the late Holocene and the Younger Dryas/GS-1, as well as floating tree chronologies for the Bølling/GI-1e and the last glacial period, means IntCal20 has considerably more detailed structure than previously provided in IntCal13;
2. The use of the Bayesian spline methodology in curve construction has allowed for predictive intervals for the curve that are able to account for over-dispersion seen within 14C tree-ring determinations from the same calendar year; enabled the better representation of rapid events; as well as isolated real signals from noise, in many cases made possible through synchronizing fluctuations within their calendar age uncertainty;
3. The incorporation of the LSG model MRA (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue; Heaton et al. Reference Heaton, Blaauw, Blackwell, Bronk Ramsey, Reimer and Scott2020b in this issue) has resulted in convergence and better agreement between marine data and the other datasets;
4. The incorporation of new Hulu Cave data has allowed for the revision of the Suigetsu timescale and a curve extension to ca. 54 cal kBP (with Cariaco Basin data alone extending to 55 cal kBP); and
5. The increased 14C measuring precision allows detection of subtle regional and seasonal fluctuations in natural 14C concentrations. These need to be considered in determining the overall uncertainty of a calibration using the global IntCal20 calibration.
Implications for Archaeology and Earth Science
The IntCal20 curve provides meaningful differences regarding the timing of the beginning and end of the Younger Dryas/GS-1 cold period in paleoenvironmental records. The increased details in the curve may lead to more complex, multimodal calibrated age probability distributions that may require stratigraphic information to resolve. These differences, as well as revisions to the calibration curve in the last glacial period, may have implications for the relative timing of 14C-dated environmental or archaeological records when these are compared to those on different timescales (e.g. ice core records). 14C calibrations with IntCal20 will also differ from those with IntCal13 for almost all time periods prior to the late Holocene. This is an important consideration given even small changes in the curve can have a large effect on archaeological chronologies where Bayesian analysis is used to estimate time spans on the order of a human lifetime or less.
The higher-resolution data and revised positioning of some of the European tree-ring chronologies allows for more precise correlation of archaeological records to those on different timescales (e.g. ice core records).
Specific examples of the difference in calibrations with the IntCal13 and IntCal20 curves are provided in van der Plicht et al. (Reference van der Plicht, Bronk Ramsey, Heaton, Scott and Talamo2020 in this issue).
Future Directions
The largest changes in the IntCal20 calibration curve are during the last glacial period, particularly older than 30 cal kBP. Because the older portion of the new curve is based directly or indirectly on the U-Th timescale, a transfer function to the ice core GICC05 timescale will be possible (Adolphi et al. Reference Adolphi, Bronk Ramsey, Erhardt, Edwards, Cheng, Turney, Cooper, Svensson, Rasmussen and Fischer2018). This should allow better comparison between 14C ages and paleoclimate records (Muscheler et al. Reference Muscheler, Adolphi, Heaton, Bronk Ramsey, Svensson, van der Plicht and Reimer2020 in this issue). In addition, geomagnetic excursions may prove to be of increasing importance for aligning different 14C datasets and ultimately correlation to ice core records via 10Be (Muscheler et al. Reference Muscheler, Adolphi, Heaton, Bronk Ramsey, Svensson, van der Plicht and Reimer2020 in this issue) or in marine sediments where the geomagnetic excursion is recorded in sediment component magnetization direction and its associated 14C signature can be found in the same records, such as in Channell et al. (Reference Channell, Harrison, Lascu, McCave, Hibbert and Austin2016).
The use of a modeled MRA improved the fit of the current marine records with other datasets, helping identify true signals. We used the glacial scenario (GS) for our model MRA corrections for the marine data. In the future it may be possible to replace the Hulu-based 14C curve by a truly atmospheric input as the driver and switch between scenarios within the Bayesian model based on climate proxies. Higher resolution models may also be able to resolve smaller regions of the ocean such as the Cariaco Basin (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020 in this issue).
Ultimately the IWG would hope to provide fully atmospheric curves for the Northern and Southern Hemispheres without reliance on more indirect records such as speleothems or marine data. In the absence of continuous dendrochronologically dated tree rings through the 14C timescale, floating tree-ring series in combination with other time scales (e.g. linked via 10Be to ice core time scales) hold the best possibility to improve the calibration curve in the future, using the other datasets as a backbone.
Single tree-ring measurements, covering over 3000 years across various time periods, from multi-region, securely dated, tree-ring chronologies have made a significant impact on this update of the curve, particularly in resolving rapid events and helping to understand their underlying processes. Given this demonstrated potential from both calendar dated and floating tree ring sequences and in anticipation of the inclusion of an even larger number of such data in future iterations of the calibration curve, the IntCal working group is developing a series of standardized procedures surrounding the creation and submission of such data. In addition to referencing previously published requirements for the submission of IntCal data (Reimer et al. Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Brown, Buck, Edwards and Friedrich2013a) this includes extra steps to avoid any ambiguity when working with trees dated using the different methodological procedures necessitated by different species at different laboratories. For example, cross-checking on nomenclature used to assign dated years as astronomical dates (including a “year 0” BC) or as AD/BC with no zero year, and making sure there is a clear statement of this associated with the submitted data, metadata, dissected samples and remnant material (retained at the tree ring host institution). As for all IntCal data the aim is to move towards improved data stewardship and public archiving or open access in line with recent standards (Kaufman et al. Reference Kaufman, Abram, Evans, Francus, Goosse, Linderholm, Loutre, Martrat, McGregor and Neukom2018). By standardizing the criteria required for the preparation of tree-ring samples for annual 14C analysis and the submission of these data and metadata to IntCal the aim is to ensure the very best compliance in open-data standards. The dendrochronological community has a data-standard (Jansma et al. Reference Jansma, Brewer and Zandhuis2010), a range of open-source tools (Tyers and Jansma Reference Tyers and Jansma2011) and data repositories (e.g. the International Tree-Ring Data Bank—ITRDB, and the Digital Collaboratory for Cultural Dendrochronology—DCCD; Jansma et al. Reference Jansma, van Lanen, Brewer and Kramer2012) but, because of the importance of full transparency with annual 14C data for any IntCal submitted data, we now also require reports from the tree-ring laboratory in which the dendrochronological dating was carried out which include meta data, raw ring width or δ18O measurements and cross-correlation statistics. At present the IntCal20 database is not set up to make this collected information accessible, but future database development, perhaps utilizing the IntChron framework initiative (Bronk Ramsey et al. Reference Bronk Ramsey, Blaauw, Kearney and Staff2019) or partnering with the ITRDB, will address this pressing requirement.
The value of identifying more rapid 14C events in the annual records from tree rings is hard to overstate. These features are of multidisciplinary significance. The potential of annual 14C data to further refine what we know about regional, latitudinal or altitudinal differences in 14C and to improve the shape of the calibration curve (particularly across transitional areas—from slopes to plateaus) has been explored but has opened up a whole new range of questions. In terms of calibration a more highly resolved curve shape produced by annually based data may be a more accurate representation of past 14C variations but depending on final shape may actually result in multimodal probability distributions. While opportunities for high-resolution wiggle-matching may be increased for certain samples, precision may be decreased or multiple different possibilities returned for other scenarios. Comparison of annual data from contemporary tree rings analyzed at multiple laboratories should also be used to more fully explore issues of error and reproducibility between laboratories for such data and could be developed to better inform error estimations for Bayesian modeling for “annual” samples. In addition, with decreased measurement uncertainties it may be possible to check the assumption that the Northern Hemisphere atmosphere is well-mixed. This has already been questioned for some regions, but further laboratory inter-comparisons are needed to ascertain whether differences seen between geographic regions are due to laboratory offsets or represent genuine offsets, the latter potentially requiring the development of region-specific calibration curves. Now that there is the capacity and capability available to measure large numbers of annual samples at sufficiently high precision (Capano et al. Reference Capano, Miramont, Shindo, Guibal, Marschal, Kromer, Tuna and Bard2019 in this issue; Sookdeo et al. Reference Sookdeo, Kromer, Buentgen, Friedrich, Friedrich, Helle, Pauly, Nievergelt, Reinig, Treydte, Synal and Wacker2019 in this issue), these are likely to be important areas of research in the future.
ACKNOWLEDGMENTS
We are grateful to the dendrochronologists who provided information on the various trees including Christopher Baisan, Peter Brewer, David Frank and Irina Panyushkina (University of Arizona), David Brown (Queen’s University Belfast), Claudia Baittinger (National Museum of Denmark), Esther Jansma (Stichting Nederlands Centrum voor Dendrochronologie), Kurt Nicolussi (Universität Innsbruck), Cathy Tyers (Historic England), Dominique Arseneault (Université du Québec), Bao Yang (Chinese Academy of Sciences), Paul Krusic (University of Cambridge), Mauro Bernabei (Italian National Research Council), Jan Esper (Johannes Gutenberg-Universität Mainz), Greg Wiles (The College of Wooster), Amy Hessl (West Virginia University), Rashit Hantemirov (Russian Academy of Sciences), Niels Bleicher (Center for Underwater Archaeology and Dendroarchaeology Zürich), Henri Grissino-Mayer (formerly of University of Tennessee), Neil Loader (University of Swansea), Takumi Mitsutani (Nara National Research Institute for Cultural Properties), Katsuhiko Kimura (Fukushima University), Takeshi Nakatsuka (Nagoya University), Masataka Hakozaki (National Museum of Japanese History), and Cécile Miramont, Lisa Shindo, Frédéric Guibal (Aix-Marseille University, Avignon University). We also acknowledge the many useful discussions with members of the IntCal focus groups and others in the scientific community. We thank Catherine Kissel and Carlo Laj for useful information about the GLOPIS curve and Darryl Granger for his insight into the geology of Hulu Cave. We also are grateful to Barbara Wohlfarth for the very thorough and constructive review.
We would like to thank the National Natural Science Foundation of China grants NSFC 41888101 and NSFC 41731174, the 111 program of China (D19002), U.S. NSF Grant 1702816, and the Malcolm H. Wiener Foundation for support for research that contributed to the IntCal20 curve. The work on the Swiss and German YD trees was funded by the German Science foundation and the Swiss National Foundation (grant number: 200021L_157187). The operation in Aix-en-Provence is funded by the EQUIPEX ASTER-CEREGE, the Collège de France and the ANR project CARBOTRYDH (to EB). The work on the correlation of tree ring 14C with ice core 10Be was partially supported by the Swedish Research Council and the Knut and Alice Wallenberg foundation. M. Butzin was supported by the German Federal Ministry of Education and Research (BMBF) as Research for Sustainable Development (FONA; http://www.fona.de) through the PalMod project (grant number: 01LP1505B). S. Talamo and M. Friedrich are funded by the European Research Council under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement No. 803147-RESOLUTION, awarded to ST). CA. Turney would like to acknowledge support of the Australian Research Council (FL100100195 and DP170104665). P. Reimer and W. Austin acknowledge the support of the UKRI Natural Environment Research Council (Grant NE/M004619/1). T.J. Heaton is supported by a Leverhulme Trust Fellowship RF-2019-140\9. Other datasets and the IntCal20 database were created without external support through internal funding by the respective laboratories. We also would like to thank various institutions that provided funding or facilities for meetings.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit https://doi.org/10.1017/RDC.2020.41