Given a graph G = (V,E) and a “cost function” $f: 2^V\rightarrow\mathbb{R}$ (provided by an oracle), the problem [PCliqW] consists in finding a partition into cliques of V(G) of minimum cost. Here, the cost of a partition is the sum of the costs of the cliques in the partition. We provide a polynomial time dynamic program for the case where G is an interval graph and f belongs to a subclass of submodular set functions, which we call “value-polymatroidal”. This provides a common solution for various generalizations of the coloring problem in co-interval graphs such as max-coloring, “Greene-Kleitman's dual”, probabilist coloring and chromatic entropy. In the last two cases, this is the first polytime algorithm for co-interval graphs. In contrast, NP-hardness of related problems is discussed. 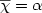We also describe an ILP formulation for [PCliqW] which gives a common polyhedral framework to express min-max relations such as ${\overline{\chi}}=\alpha$ for perfect graphs and the polymatroid intersection theorem. This approach allows to provide a min-max formula for [PCliqW] if G is the line-graph of a bipartite graph and f is submodular. However, this approach fails to provide a min-max relation for [PCliqW] if G is an interval graphs and f is value-polymatroidal.