Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T21:42:01.263Z Has data issue: false hasContentIssue false
  • English
  • Français

The Riemann problem for a system of conservation laws of mixed type with a cubic nonlinearity

Published online by Cambridge University Press:  14 November 2011

Michael Shearer  and
Yadong Yang
Michael Shearer
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695, U.S.A.
Yadong Yang
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Using the viscosity-capillarity admissibility criterion for shock waves, we solve the Riemann problem for the system of conservation laws

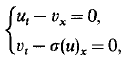
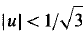where σ(u) = u3 − u. This system is hyperbolic at (u, v) unless . We find that the Riemann problem has a unique solution for all data in the hyperbolic regions, except for a range of data in the same phase (i.e. on the same side of the nonhyperbolic strip). In the nonunique cases, there are exactly two admissible solutions. The analysis is based upon a formula describing all saddle-to-saddle heteroclinic orbits for a family of cubic vector fields in the plane.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 4 , 1995 , pp. 675 - 699
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abeyaratne, R. and Knowles, J. K.. Kinetic relations and the propagation of phase boundaries in solids. Arch. Rational Meek Anal. 114 (1991), 119–54.CrossRefGoogle Scholar
2Abeyaratne, R. and Knowles, J. K.. Implications of viscosity and strain gradient effects for the kinetics of propagating phase boundaries in solids. SIAM J. Appl. Math. 51 (1991), 1205–21.CrossRefGoogle Scholar
3Abeyaratne, R. and Knowles, J. K.. On the propagation of maximally dissipative phase boundaries in solids. Q. Appl. Math. 50 (1992), 149–72.CrossRefGoogle Scholar
4Chicone, C. C.. Quadratic gradients on the plane are generically Morse–Smale. J. Differential Equations 33 (1979), 159–66.CrossRefGoogle Scholar
5Greenberg, J. M.. Hyperbolic heat transfer problems with phase transitions. In Proceedings of the Second International Conference on Nonlinear Hyperbolic Problems, Aachen, Notes in Fluid Mechanics 24 (1988), 186–92.Google Scholar
6Isaacson, E., Marchesin, D. and Plohr, B.. Transitional waves for conservation laws. SIAM J. Math. Anal. 21 (1990), 837–66.CrossRefGoogle Scholar
7Jacobs, D., McKinney, W. and Shearer, M.. Travelling wave solutions of the modified KortewegdeVries–Burgers equation. J. Differential Equations 116 (1995), 448–67.CrossRefGoogle Scholar
8Lax, P. D.. Hyperbolic systems of conservation laws II. Comm. Pure Appl. Math. 10 (1957), 537–66.CrossRefGoogle Scholar
9Liu, T.-P.. The Riemann problem for general 2 × 2 conservation laws. Trans. Amer. Math. Soc. 199 (1974), 89–112.Google Scholar
10Pego, R. L.. Phase transitions in one-dimensional nonlinear viscoelasticity: admissibility and stability. Arch. Rational Mech. Anal. 97 (1987), 353–94.CrossRefGoogle Scholar
11Schecter, S.. Pitchfork bifurcation with a heteroclinic orbit: normal form, recognition, and universal unfolding. J. Differential Equations 105 (1993), 63–93.CrossRefGoogle Scholar
12Shearer, M.. The Riemann problem for a class of conservation laws of mixed type. J. Differential Equations 46 (1982), 426–43.CrossRefGoogle Scholar
13Shearer, M.. Nonuniqueness of admissible solutions of Riemann initial value problems for a system of conservation laws of mixed type. Arch. Rational Mech. Anal. 93 (1986), 45–59.CrossRefGoogle Scholar
14Shearer, M.. The Riemann problem for 2 × 2 systems of hyperbolic conservation laws with case I quadratic nonlinearities. J. Differential Equations 80 (1989), 343–63.CrossRefGoogle Scholar
15Shearer, M. and Schecter, S.. Transversality for undercompressive shocks in Riemann problems. In Viscous Profiles and Numerical Methods for Shock Waves, ed. Shearer, M., pp. 209–36 (Philadelphia, PA: SIAM, 1991).Google Scholar
16Slemrod, M.. Admissibility criteria for propagating phase boundaries in a van der Waals fluid. Arch. Rational Mech. Anal. 81 (1983), 301–15.CrossRefGoogle Scholar
17Smoller, J.. Shock Waves and Reaction-Diffusion Equations (Berlin: Springer, 1983).CrossRefGoogle Scholar
18Truskinovsky, L. M.. Dynamics of non-equilibrium phase boundaries in a heat conducting nonlinearly elastic medium. PMM U.S.S.R. 51 (1987), 777–84.Google Scholar
19Wendroff, B.. The Riemann problem for materials with nonconvex equations of state. I: Isentropic flow. J. Math. Anal. Appl. 38 (1972), 454–66.CrossRefGoogle Scholar
20Yang, Y.. Explicit Solutions of a Class of Riemann Problems of Mixed Type (Ph.D. Thesis, N.C. State University, 1991).Google Scholar