No CrossRef data available.
Article contents
UNIQUENESS THEOREMS FOR MAPPINGS OF FINITE DISTORTION
Part of:
Geometric function theory
Published online by Cambridge University Press: 07 November 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we prove uniqueness theorems for mappings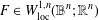 
$F\in W_{\text{loc}}^{1,n}(\mathbb{B}^{n};\mathbb{R}^{n})$ of finite distortion 
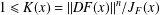$1\leq K(x)=\Vert \mathit{DF}(x)\Vert ^{n}/J_{F}(x)$ satisfying some integrability conditions. These types of theorems fundamentally state that if a mapping defined in 
$\mathbb{B}^{n}$ has the same boundary limit 
$a$ on a ‘relatively large’ set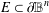 
$E\subset \unicode[STIX]{x2202}\mathbb{B}^{n}$, then the mapping is constant. Here the size of the set 
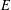$E$ is measured in terms of its 
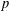$p$-capacity or equivalently its Hausdorff dimension.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
References
Brelot, M. and Doob, J. L., ‘Limites angulaires et limites fines’, Ann. Inst. Fourier (Grenoble)
13 (1963), 395–415.Google Scholar
Carleson, L., ‘Sets of uniqueness for functions analytic in the unit disc’, Acta Math.
87 (1952), 325–345.CrossRefGoogle Scholar
Doob, J. L., Classical Potential Theory and its Probabilistic Counterpart (Springer, New York, 1984).Google Scholar
Fuglede, B., ‘Extremal length and functional completion’, Acta Math.
98 (1957), 171–219.Google Scholar
Goldstein, V. and Vodopyanov, S., ‘Quasiconformal mappings and spaces of functions with generalized first derivatives’, Sibirsk. Mat. Zh.
17 (1976), 515–531.Google Scholar
Heinonen, J., Kilpeläinen, T. and Martio, O., Nonlinear Potential Theory (Oxford University Press, New York, 1993).Google Scholar
Heinonen, J. and Koskela, P., ‘Quasiconformal maps in metric spaces with controlled geometry’, Acta Math.
181 (1998), 1–61.CrossRefGoogle Scholar
Jenkins, J. A., ‘On a result of Beurling’, Indiana Univ. Math. J.
41 (1992), 1077–1080.Google Scholar
Koskela, P., ‘A radial uniqueness theorem for Sobolev functions’, Bull. Lond. Math. Soc.
27 (1995), 460–466.Google Scholar
Manfredi, J. and Villamor, E., ‘Traces of monotone Sobolev functions’, J. Geom. Anal.
6(3) (1996), 433–444.CrossRefGoogle Scholar
Manfredi, J. J. and Villamor, E., ‘Traces of monotone functions in weighted Sobolev spaces’, Illinois J. Math.
45 (2001), 403–422.CrossRefGoogle Scholar
Miklyukov, V. M. and Vuorinen, M., ‘A boundary uniqueness theorem for Sobolev functions’, Tohoku Math. J.
50 (1998), 503–511.Google Scholar
Mizuta, Y., ‘Remarks on the results by Koskela concerning the radial uniqueness for Sobolev functions’, Proc. Amer. Math. Soc.
126 (1998), 1043–1047.CrossRefGoogle Scholar
Ohtsuka, M., ‘On weighted extremal length of families of curves’, in: Complex Analysis (Birkhauser, Basel, 1988), 191–200.Google Scholar
Tsuji, M., ‘Beurling’s theorem on exceptional sets’, Tohoku Math. J.
2 (1950), 113–125.Google Scholar
Väisälä, J., Lectures in n-Dimensional Quasiconformal Mappings, Lecture Notes, 229 (Springer, Berlin, 1971).CrossRefGoogle Scholar
Villamor, E., ‘Boundary values for some classes of functions’, J. Lond. Math. Soc.
45 (1992), 508–518.Google Scholar
Vuorinen, M., ‘On the existence of angular limits of n-dimensional quasiregular mappings’, Ark. Mat.
18 (1980), 157–180.CrossRefGoogle Scholar
Yamamoto, H., ‘On weighted extremal length and p-capacity’, Hiroshima Math. J.
20 (1990), 633–642.CrossRefGoogle Scholar
You have
Access