Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T22:52:18.241Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGH-ORDER UPWIND FINITE VOLUME ELEMENT METHOD FOR FIRST-ORDER HYPERBOLIC OPTIMAL CONTROL PROBLEMS

Part of: Optimality conditions Partial differential equations, boundary value problems Existence theories

Published online by Cambridge University Press:  11 April 2016

QIAN ZHANG Open the ORCID record for QIAN ZHANG [Opens in a new window] ,
JINLIANG YAN Open the ORCID record for JINLIANG YAN [Opens in a new window]  and
ZHIYUE ZHANG Open the ORCID record for ZHIYUE ZHANG [Opens in a new window]
QIAN ZHANG
Affiliation:
School of Mathematical Sciences, Jiangsu Key Laboratory for NSLSCS, Nanjing Normal University, Nanjing 210023, China email zhangqian7452019@126.com, zhangzhiyue@njnu.edu.cn
JINLIANG YAN
Affiliation:
Department of Mathematics and Computer, Wuyi University, Wuyishan 354300, China email yanjinliang3333@163.com
ZHIYUE ZHANG*
Affiliation:
School of Mathematical Sciences, Jiangsu Key Laboratory for NSLSCS, Nanjing Normal University, Nanjing 210023, China email zhangqian7452019@126.com, zhangzhiyue@njnu.edu.cn
*
✉zhangzhiyue@njnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a high-order upwind finite volume element method to solve optimal control problems governed by first-order hyperbolic equations. The method is efficient and easy for implementation. Both the semi-discrete error estimates and the fully discrete error estimates are derived. Optimal order error estimates in the sense of 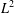$L^{2}$-norm are obtained. Numerical examples are provided to confirm the effectiveness of the method and the theoretical results.

Keywords

optimizationvariational discretizationhigh-order upwind finite volume elementhyperbolic optimal control

MSC classification

Primary: 65N15: Error bounds
Secondary: 49K20: Problems involving partial differential equations 49J20: Optimal control problems involving partial differential equations 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods
Type
Research Article
Information
The ANZIAM Journal , Volume 57 , Issue 4 , April 2016 , pp. 482 - 498
Copyright
© 2016 Australian Mathematical Society 

References

Adams, R. A. and Fournier, J. J. F., Sobolev spaces (Academic Press, New York, 2003).Google Scholar
Castillo, P., Cockburn, B., Perugia, I. and Schötzau, D., “An a priori error analysis of the local discontinuous Galerkin method for elliptic problems”, SIAM J. Numer. Anal. 38 (2000) 1676–1706; doi:10.1137/S0036142900371003.CrossRefGoogle Scholar
Chen, Y., Yi, N. and Liu, W., “A Legendre–Galerkin spectral method for optimal control problems governed by elliptic equations”, SIAM J. Numer. Anal. 46 (2008) 2254–2275; doi:10.1137/070679703.Google Scholar
Christofides, P. D., Nonlinear and robust control of PDE systems: methods and applications to transport–reaction processes (Birkhäuser, Basel, 2001); doi:10.1115/1.1451164.Google Scholar
Hinze, M., “A variational discretization concept in control constrained optimization: the linear–quadratic case”, Comput. Optim. Appl. 30 (2005) 45–61; doi:10.1007/s10589-005-4559-5.Google Scholar
Hinze, M., Pinnau, R., Ulbrich, M. and Ulbrich, S., Optimization with PDE constraints, Volume 23 of Mathematical Modelling: Theory and Applications (Springer, Netherlands, 2009).Google Scholar
Ito, K. and Kunisch, K., “Lagrange multiplier approach to variational problems and applications”, in: Advances in Design and Control, Volume 15 (SIAM, Philadelphia, PA, 2008).Google Scholar
Li, R., Chen, Z. and Wu, W., Generalized difference methods for differential equations: numerical analysis of finite volume methods, Volume 226 (CRC Press, Florida, 2000).CrossRefGoogle Scholar
Lions, J. L., “Optimal control of systems governed by partial differential equations”, in: Grundlehren der mathematischen Wissenschaften (trans. S. K. Mitter), Volume 170 (Springer, Berlin–Heidelberg, 1971).Google Scholar
Lions, J. L., Magenes, E. and Kenneth, P., Non-homogeneous boundary value problems and applications, Volume 1 (Springer, Berlin, 1972).Google Scholar
Luo, X., Chen, Y. and Huang, Y., “A priori error estimates of finite volume element method for hyperbolic optimal control problems”, Sci. China Math. 56 (2013) 901–914; doi:10.1007/s11425-013-4573-5.CrossRefGoogle Scholar
Meidner, D. and Vexler, B., “A priori error estimates for space–time finite element discretization of parabolic optimal control problems. Part II: problems with control constraints”, SIAM J. Control Optim. 47 (2008) 1301–1329; doi:10.1137/070694028.CrossRefGoogle Scholar
Singh, P. and Sharma, K. K., “Numerical approximations to the transport equation arising in neuronal variability”, Int. J. Pure Appl. Math. 69 (2011) 341–356; http://www.ijpam.eu/contents/2011-69-3/8/8.pdf.Google Scholar
Tröltzsch, F., Optimal control of partial differential equations: theory, methods, and applications, Volume 112 of Graduate Studies in Mathematics (trans. Jürgen Sprekels) (American Mathematical Society, Providence, RI, 2010).Google Scholar
Ulbrich, S., “A sensitivity and adjoint calculus for discontinuous solutions of hyperbolic conservation laws with source terms”, SIAM J. Control Optim. 41 (2002) 740–797; doi:10.1137/S0363012900370764.Google Scholar
Wang, L. and Xu, X., The mathematical foundation of finite element methods (in Chinese) (Science Press, Beijing, 2004).Google Scholar
Wang, P. and Zhang, Z., “Quadratic finite volume element method for the air pollution model”, Int. J. Comput. Math. 87 (2010) 2925–2944; doi:10.1080/00207160802680663.Google Scholar
Wang, Q., Lin, S. and Zhang, Z., “Numerical methods for a fluid mixture model”, Internat. J. Numer. Methods Fluids 71 (2013) 1–12; doi:10.1002/fld.3639.Google Scholar
Wheeler, M. F., “A priori $L_{2}$ error estimates for Galerkin approximations to parabolic partial differential equations”, SIAM J. Numer. Anal. 10 (1973) 723–759; doi:10.1137/0710062.Google Scholar