Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-27T04:43:47.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for general size distributions

Published online by Cambridge University Press:  14 July 2016

Wen-Chen Chen
Wen-Chen Chen*
Affiliation:
Carnegie–Mellon University
*
∗Postal address: Department of Statistics, Carnegie–Mellon University, Schenley Park, Pittsburgh, PA 15213, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X1, X2, · ··, Xn, · ·· be independent and identically distributed non-negative integer-valued random variables with finite mean and variance. For any positive integer n and m we consider the random vector 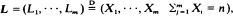i.e., L has the same distribution as the conditional distribution of (X1, · ··, Xm) given the condition 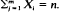It is easy to see that our model includes the classical urn model, the Bose–Einstein urn model and the Pólya urn model as special cases. For any non-negative integer s define G(s) = the number of Li′s such that Li = s, and U = the number of Li′s such that Li is an even number; in this paper we study the asymptotic behaviour of the random variables considered above. Some central limit theorems and a multinormal local limit theorem are proved.

Keywords

BOSE-EINSTEIN URN MODELCLASSICAL URN MODELCENTRAL LIMIT THEOREMLOCAL LIMIT THEOREMPÓLYA URN MODELPROBABILITY GENERATING FUNCTIONSADDLE POINT METHOD
Type
Research Papers
Information
Journal of Applied Probability , Volume 18 , Issue 1 , March 1981 , pp. 139 - 147
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bekessy, A. (1963) On classical occupancy problems I. Magyar Tud. Akad. Mat. Kutato Int. Kozl. 8, 59–71.Google Scholar
[2] Chen, W. C. (1980) On the weak form of Zipf's law. J. Appl. Prob. 17, 611–622.Google Scholar
[3] Chen, W. C. (1979) Some local limit theorems in the symmetric Dirichlet–multinomial urn models. Technical Report No. 156, Dept. of Statistics, Carnegie-Mellon University, Pittsburgh, PA.Google Scholar
[4] Daniels, H. E. (1958) Discussion of Cox, D. R., The regression analysis of binary sequences. J. R. Statist. Soc. B 20, 215–242.Google Scholar
[5] Darling, D. A. (1968) Some limit theorems associated with multinomial trials. Proc. 5th Berkeley Symp. Math. Statist. Prob. 2, 345–350.Google Scholar
[6] David, F. N. and Barton, P. E. (1962) Combinatorial Chance. Griffin, London.Google Scholar
[7] Gnedenko, B. V. (1962) The Theory of Probability. Chelsea, New York.Google Scholar
[8] Holst, L. (1979) Two conditional limit theorems with applications. Ann. Statist. 7, 551–557.Google Scholar
[9] Johnson, N. L. and Kotz, S. (1977) Urn Models and their Applications. Wiley, New York.Google Scholar
[10] Karlin, S. (1967) Central limit theorems for certain infinite urn schemes. J. Math. Mech. 17, 373–401.Google Scholar
[11] Mosimann, J. E. (1962) On the compound multinomial distribution, the multivariate ß -distribution, and correlations among proportions. Biometrika 49, 65–82.Google Scholar
[12] Mosimann, J. E. (1963) On the compound negative multinomial distribution and correlations among inversely sampled pollen counts. Biometrika 50, 47–54.CrossRefGoogle Scholar
[13] Pólya, G. (1931) Sur quelques points de la théorie des probabilités. Ann. Inst. H. Poincaré 1, 117–161.Google Scholar
[14] Renyi, A. (1962) Three new proofs and a generalization of a theorem of Irving Weiss. Magyar Tud. Akad. Mat. Kutato Int. Kozl. 7, 203–214.Google Scholar
[15] Sevastyanov, B. A. and Chistyakov, V. P. (1964) Asymptotic normality in the classical ball problem. Theory Prob. Appl. 9, 198–211.CrossRefGoogle Scholar
[16] Spitzer, F. (1964) Principles of Random Walk. Van Nostrand, New York.Google Scholar
[17] Weiss, I. (1958) Limiting distribution in some occupancy problems. Ann. Math. Statist. 29, 878–884.Google Scholar