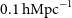84 results
Community respiratory viral metrics to inform masking in healthcare settings: A regional consensus approach
-
- Journal:
- Infection Control & Hospital Epidemiology , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Figures
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp vii-viii
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp xv-xvi
-
- Chapter
- Export citation
Chapter 5 - Benford Agreement Analysis of the Sea Around Us Project’s Fish-Landings Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 94-130
-
- Chapter
- Export citation
Chapter 4 - Data Characteristics and the Workflow of Benford Agreement Analysis
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 74-93
-
- Chapter
- Export citation
Chapter 7 - Assessing the Impacts of Problematic Benford Validity
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 169-187
-
- Chapter
- Export citation
Index
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 204-208
-
- Chapter
- Export citation
Chapter 3 - Benford’s Law and Assessing Conformity
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 24-73
-
- Chapter
- Export citation
Preface
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp xiii-xiv
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp iv-iv
-
- Chapter
- Export citation
Chapter 6 - Benford Agreement Analysis of US and Global COVID-19 New Cases Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 131-168
-
- Chapter
- Export citation
References
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 196-203
-
- Chapter
- Export citation
Tables
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp ix-xii
-
- Chapter
- Export citation
Chapter 1 - Introduction
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 1-10
-
- Chapter
-
- You have access
- HTML
- Export citation
Contents
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp v-vi
-
- Chapter
- Export citation
Chapter 2 - Validity and Self-Reported Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 11-23
-
- Chapter
-
- You have access
- HTML
- Export citation
Chapter 8 - Conclusion
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 188-195
-
- Chapter
- Export citation

Applying Benford's Law for Assessing the Validity of Social Science Data
-
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023
Optimising MWA EoR data processing for improved 21-cm power spectrum measurements—fine-tuning ionospheric corrections
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 39 / 2022
- Published online by Cambridge University Press:
- 14 October 2022, e047
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A comparison of grazing v. zero-grazing on early-lactation dairy cow performance
-
- Journal:
- The Journal of Agricultural Science / Volume 160 / Issue 1-2 / February 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 127-136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation