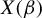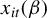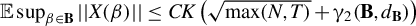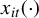9 results
SEQUENTIALLY ESTIMATING THE STRUCTURAL EQUATION BY POWER TRANSFORMATION
-
- Journal:
- Econometric Theory / Volume 40 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 September 2022, pp. 98-161
-
- Article
- Export citation
A UNIFORM BOUND ON THE OPERATOR NORM OF SUB-GAUSSIAN RANDOM MATRICES AND ITS APPLICATIONS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1073-1091
-
- Article
- Export citation
DYNAMIC LINEAR PANEL REGRESSION MODELS WITH INTERACTIVE FIXED EFFECTS
-
- Journal:
- Econometric Theory / Volume 33 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 December 2015, pp. 158-195
-
- Article
- Export citation
PETER C.B. PHILLIPS’S CONTRIBUTIONS TO PANEL DATA METHODS
-
- Journal:
- Econometric Theory / Volume 30 / Issue 4 / August 2014
- Published online by Cambridge University Press:
- 24 February 2014, pp. 882-893
-
- Article
- Export citation
PANEL DATA MODELS WITH FINITE NUMBER OF MULTIPLE EQUILIBRIA
-
- Journal:
- Econometric Theory / Volume 26 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 07 October 2009, pp. 863-881
-
- Article
- Export citation
A STUDY OF A SEMIPARAMETRIC BINARY CHOICE MODEL WITH INTEGRATED COVARIATES
-
- Journal:
- Econometric Theory / Volume 22 / Issue 4 / August 2006
- Published online by Cambridge University Press:
- 23 May 2006, pp. 721-742
-
- Article
- Export citation
REDUCING BIAS OF MLE IN A DYNAMIC PANEL MODEL
-
- Journal:
- Econometric Theory / Volume 22 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 15 March 2006, pp. 499-512
-
- Article
- Export citation
MINIMUM DISTANCE ESTIMATION OF NONSTATIONARY TIME SERIES MODELS
-
- Journal:
- Econometric Theory / Volume 18 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 24 September 2002, pp. 1385-1407
-
- Article
- Export citation
HOW TO ESTIMATE AUTOREGRESSIVE ROOTS NEAR UNITY
-
- Journal:
- Econometric Theory / Volume 17 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 07 February 2001, pp. 29-69
-
- Article
- Export citation