Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T19:41:46.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Lattice Tilings in Euclidean Spaces

Part of: Real and complex geometry Designs and configurations Discrete geometry

Published online by Cambridge University Press:  16 November 2018

Qi Yang  and
Chuanming Zong
Qi Yang
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China
Chuanming Zong
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, China Email: cmzong@math.pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1885, Fedorov discovered that a convex domain can form a lattice tiling of the Euclidean plane if and only if it is a parallelogram or a centrally symmetric hexagon. This paper proves the following results. Except for parallelograms and centrally symmetric hexagons, there are no other convex domains that can form two-, three- or four-fold lattice tilings in the Euclidean plane. However, there are both octagons and decagons that can form five-fold lattice tilings. Whenever 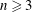$n\geqslant 3$, there are non-parallelohedral polytopes that can form five-fold lattice tilings in the $n$-dimensional Euclidean space.

MSC classification

Primary: 52C20: Tilings in $2$ dimensions
Secondary: 52C22: Tilings in $n$ dimensions 05B45: Tessellation and tiling problems 52C17: Packing and covering in $n$ dimensions 51M20: Polyhedra and polytopes; regular figures, division of spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 923 - 929
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by 973 Program 2013CB834201. Author C. Z. is the corresponding author.

References

Aleksandrov, A. D., On completion of a space by polyhedra . Vestnik Leningrad Univ. Ser. Mat. Fiz. Him. 9(1954), 33–43.Google Scholar
Blunden, W. J., Multiple covering of the plane by circles . Mathematika 4(1957), 7–16. http://doi.org/10.1112/S0025579300001042 Google Scholar
Blunden, W. J., Multiple packing of circles in the plane . J. London Math. Soc. 38(1963), 176–182. http://doi.org/10.1112/jlms/s1-38.1.176 Google Scholar
Bolle, U., On the density of multiple packings and coverings of convex discs . Studia Sci. Math. Hungar. 24(1989), 119–126.Google Scholar
Bolle, U., On multiple tiles in E 2 . In: Intuitive geometry, Colloq. Math. Soc. J. Bolyai, 63. North-Holland, Amsterdam, 1994.Google Scholar
Cohn, M. J., Multiple lattice covering of space . Proc. London Math. Soc. 32(1976), 117–132. http://doi.org/10.1112/plms/s3-32.1.117 Google Scholar
Delone, B. N., Sur la partition regulière de l’espace à 4 dimensions I, II . Izv. Akad. Nauk SSSR, Ser. VII (1929), 79–110, 147–164.Google Scholar
Dumir, V. C. and Hans-Gill, R. J., Lattice double packings in the plane . Indian J. Pure Appl. Math. 3(1972), 481–487.Google Scholar
Dutour Sikirić, M., Garber, A., Schürmann, A., and Waldmann, C., The complete classification of five-dimensional Dirichlet–Voronoi polyhedra of translational lattices . Acta Crystallogr. A72(2016), 673–683. http://doi.org/10.1107/s2053273316011682 Google Scholar
Engel, P., On the symmetry classification of the four-dimensional parallelohedra . Z. Krist. 200(1992), 199–213. http://doi.org/10.1524/zkri.1992.200.3-4.199 Google Scholar
Fedorov, E. S., Elements of the study of figures . Zap. Mineral. Imper. S. Petersburgskogo Obšč. 21(1885), 1–279. Načala učeniya o figurah. (Russian) (Elements of the study of figures.) Izdat. Akad. Nauk SSSR, Moscow, 1953.Google Scholar
Fejes Tóth, G., Multiple lattice packings of symmetric convex domains in the plane . J. London Math. Soc. 29(1984), 556–561. http://doi.org/10.1112/jlms/s2-29.3.556 Google Scholar
Furtwängler, P., Über Gitter konstanter Dichte . Monatsh. Math. Phys. 43(1936), 281–288. http://doi.org/10.1007/BF01707607 Google Scholar
Gravin, N., Robins, S., and Shiryaev, D., Translational tilings by a polytope, with multiplicity . Combinatorica 32(2012), 629–649. http://doi.org/10.1007/s00493-012-2860-3 Google Scholar
Gravin, N., Kolountzakis, M. N., Robins, S., and Shiryaev, D., Structure results for multiple tilings in 3D . Discrete Comput. Geom. 50(2013), 1033–1050. http://doi.org/10.1007/s00454-013-9548-3 Google Scholar
Groemer, H., Multiple packings and coverings . Studia Sci. Math. Hungar. 21(1986), 189–200.Google Scholar
Gruber, P. M. and Lekkerkerker, C. G., Geometry of numbers . Second ed., North-Holland Mathematical Library, 37. North-Holland, Amsterdam, 1987.Google Scholar
Hajós, G., Über einfache und mehrfache Bedeckung des n-dimensionalen Raumes mit einem Würfelgitter . Math. Z. 47(1941), 427–467. http://doi.org/10.1007/BF01180974 Google Scholar
Kolountzakis, M. N., On the structure of multiple translational tilings by polygonal regions . Discrete Comput. Geom. 23(2000), 537–553. http://doi.org/10.1007/s004540010014 Google Scholar
Lagarias, J. C. and Zong, C., Mysteries in packing regular tetrahedra . Notices Amer. Math. Soc. 59(2012), 1540–1549. http://doi.org/10.1090/noti918 Google Scholar
Mann, C., McLoud-Mann, J., and Von Derau, D., Convex pentagons that admit i-block transitive tilings . Geom. Dedicata 194(2018), 141–167. http://doi.org/10.1007/s10711-017-0270-9 Google Scholar
McMullen, P., Convex bodies which tiles space by translation . Mathematika 27(1980), 113–121. http://doi.org/10.1112/S0025579300010007 Google Scholar
Minkowski, H., Allgemeine Lehrsätze über konvexen Polyeder . Nachr. K. Ges. Wiss. Göttingen, Math.-Phys. KL. (1897), 198–219.Google Scholar
Rao, M., Exhaustive search of convex pentagons which tile the plane. arxiv:1708.00274 Google Scholar
Reinhardt, K., Über die Zerlegung der Ebene in Polygone. Dissertation, Universität Frankfurt am Main, 1918.Google Scholar
Robinson, R. M., Multiple tilings of n-dimensional space by unit cubes . Math. Z. 166(1979), 225–264. http://doi.org/10.1007/BF01214145 Google Scholar
Štogrin, M. I., Regular Dirichlet–Voronoi partitions for the second triclinic group. (in Russian) In: Proceedings of the Steklov Institute of Mathematics, 123. American Mathematical Society, Providence, RI, 1975.Google Scholar
Venkov, B. A., On a class of Euclidean polytopes . Vestnik Leningrad Univ. Ser. Mat. Fiz. Him. 9(1954), 11–31.Google Scholar
Voronoi, G. F., Nouvelles applications des parammètres continus à la théorie des formes quadratiques. Deuxième Mémoire. Recherches sur les paralléloèdres primitifs . J. reine angew. Math. 134(1908), 198–287. http://doi.org/10.1515/crll.1908.134.198 Google Scholar
Zong, C., What is known about unit cubes . Bull. Amer. Math. Soc. 42(2005), 181–211. http://doi.org/10.1090/S0273-0979-05-01050-5 Google Scholar
Zong, C., The cube: a window to convex and discrete geometry . Cambridge Tracts in Mathematics, 168. Cambridge University Press, Cambridge, 2006. http://doi.org/10.1017/CBO9780511543173 Google Scholar
Zong, C., Packing, covering and tiling in two-dimensional spaces . Expo. Math. 32(2014), 297–364. http://doi.org/10.1016/j.exmath.2013.12.002 Google Scholar