Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, Peter
1978.
On the duality between the behaviour of sums of independent random variables and the sums of their squares.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 84,
Issue. 1,
p.
117.
Cohn, Harry
and
Hall, Peter
1982.
On the limit behaviour of weighted sums of random variables.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 59,
Issue. 3,
p.
319.
Chow, Yuan Shih
and
Teicher, Henry
1988.
Probability Theory.
p.
84.
Hong, Dug Hun
1996.
On the weak law of large numbers for randomly indexed partial sums for arrays.
Statistics & Probability Letters,
Vol. 28,
Issue. 2,
p.
127.
Chow, Yuan Shih
and
Teicher, Henry
1997.
Probability Theory.
p.
84.
Yaskov, Pavel
2016.
A short proof of the Marchenko–Pastur theorem.
Comptes Rendus. Mathématique,
Vol. 354,
Issue. 3,
p.
319.
Yaskov, Pavel
2016.
Necessary and sufficient conditions for the Marchenko-Pastur theorem.
Electronic Communications in Probability,
Vol. 21,
Issue. none,
Yaskov, Pavel
2018.
LLN for Quadratic Forms of Long Memory Time Series and Its Applications in Random Matrix Theory.
Journal of Theoretical Probability,
Vol. 31,
Issue. 4,
p.
2032.
de Chaisemartin, Clément
and
d'Haultfoeuille, Xavier
2020.
Difference-in-Differences Estimators of Intertemporal Treatment Effects.
SSRN Electronic Journal ,
Yaskov, P. A.
2022.
Limiting Spectral Distribution for Large Sample Covariance Matrices with Graph-Dependent Elements.
Theory of Probability & Its Applications,
Vol. 67,
Issue. 3,
p.
375.
de Chaisemartin, Clément
and
d'Haultfoeuille, Xavier
2022.
Difference-in-Differences Estimators of Intertemporal Treatment Effects.
SSRN Electronic Journal,
Yaskov, Pavel Andreevich
2022.
Предельный спектр выборочных ковариационных матриц растущей размерности с граф-зависимыми элементами.
Теория вероятностей и ее применения,
Vol. 67,
Issue. 3,
p.
471.




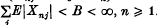 . Let
. Let