Introduction
Nonmonotonic logic (abbreviated as NML) and its domain, defeasible reasoning, are multifaceted areas. In crafting an Element that serves as both an introduction and an overview, we must adopt a specific perspective to ensure coherence and systematic coverage. It is, however, in the nature of illuminating a scenario with a spotlight that certain aspects emerge prominently, while others recede into shadow. The focus of this Element is on unveiling the core ideas and concepts underlying NML. Rather than exhaustively presenting concrete logics from existing literature, we emphasize three fundamental methods: (i) formal argumentation, (ii) consistent accumulation, and (iii) semantic approaches.
An argumentative approach for understanding human reasoning has been proposed both in a philosophical context by Toulmin’s forceful attack on formal logic in Reference Toulmin1958, and more recently in cognitive science by Mercier and Sperber (Reference Mercier and Sperber2011). Pioneers such as Pollock (Reference Pollock1991) and Dung (Reference Dung1995) have provided the foundation for a rich family of systems of formal argumentation.
Consistent accumulation methods are based on the idea that an agent facing possibly conflicting and not fully reliable information is well advised to reason on the basis of only a consistent part of that information. The agent could start with certain information and then stepwise add merely plausible information. In this way they stepwise accumulate a consistent foundation to reason with. Accumulation methods cover, for instance, Reiter’s influential default logic (Reiter, Reference Reiter1980) or methods based on maximal consistent sets, such as early logics by Rescher and Manor (Reference Rescher and Manor1970) and (constrained) input–output logic (Makinson & Van Der Torre, Reference Makinson and Van Der Torre2001).
While the previous two methods are largely based on syntactic or proof-theoretic considerations, interpretation plays the essential role in semantic approaches. The core idea is to order interpretations with respect to normality considerations and then to select sufficiently normal ones. These are used to determine the consequences of a reasoning process or to give meaning to nonmonotonic conditionals. The idea surfaces in the history of NML in many places, among others in Batens (Reference Batens1986), Gelfond and Lifschitz (Reference Gelfond and Lifschitz1988), Kraus et al. (Reference Kraus, Lehman and Magidor1990), McCarthy (Reference McCarthy1980), and Shoham (Reference Shoham and Ginsberg1987).
A central aspect of this Element is its unifying perspective (inspired by works such as Bochman (Reference Bochman2005) and Makinson (Reference Makinson2005). Defeasible reasoning gives rise to a variety of formal models based on different assumptions and approaches. Comparing these approaches can be difficult. The Element presents several translations between NMLs, illustrating that in many cases the same inferences can be validated in terms of diverse formal methods. These translations offer numerous benefits. They enrich our understanding by offering different perspectives: the same underlying inference mechanism may be considered as a form of (formal) argumentation, a way of reasoning with interpretations that are ordered with respect to their plausibility, or as a way of accumulating and reasoning with consistent subsets of a possibly inconsistent knowledge base. They demonstrate the robustness of the underlying inference mechanism, since several intuitive methods give rise to the same result. While the different methodological strands of NML have often been developed with little cross-fertilization, it is remarkable that the resulting systems can often be related with relative ease. Finally, the translations may convince the reader that, despite the fact that the field of NML seems a bit of a rag rug at first sight, there is quite some coherence when taking a deeper dive. In particular, by showcasing formal argumentation’s exceptional ability to represent other NMLs, this Element adds further evidence to the fruitfulness of Dung’s program of utilizing formal argumentation as a unifying perspective on defeasible reasoning (Dung, Reference Dung1995).
The Element is organized in four parts. Part I provides a general introduction to the topic of defeasible reasoning and NML. The three core methods are each introduced in a nutshell. It provides a condensed and self-contained overview of the fundamentals of NML for readers with limited time. Part II to IV deepen on each of the respective methods by providing metatheoretic insights and presenting concrete systems from the literature.
While some short metaproofs that contribute to an improved understanding are left in the body of the Element, two technical appendices are provided for others. In particular, results marked with ‘⋆’ are proven in the appendices.
Many important aspects and systems of NML didn’t get the spotlight and fell victim to the trade-off between systematicity and scope from which an introductory Element of this length will necessarily suffer. Nevertheless, with this Element a reader will grow the wings necessary to maneuver in the lands of nonflying birds, that is, they will be well equipped to understand, say, first-order versions of logics that are discussed here on the propositional level, or systems such as autoepistemic logic.
Part I Logics for Defeasible Reasoning
1 Defeasible Reasoning
1.1 What is Defeasible Reasoning?
We certainly want more than we can get by deduction from our evidence. … So real inference, the inference we need for the conduct of life, must be nonmonotonic.
This Element introduces logical models of defeasible reasoning, so-called NonMonotonic Logics (in short, NMLs). When we reason, we make inferences, that is, we draw conclusions from some given information or basic assumptions. Whenever we reserve the possibility to retract some inferences upon acquiring more information, we reason defeasibly.Footnote 1 Two paradigmatic examples of defeasible inferences are:
| Assumption | Defeasible conclusion | Reason for retraction |
| The streets are wet. | It rained. | The streets have been cleaned. |
| Tweety is a bird. | Tweety can fly. | Tweety is a penguin. |
As the examples highlight, we often reason defeasibly if our available information is incomplete: we lack knowledge of what happened before we observed the wet streets, or we lack knowledge of what kind of bird Tweety is. Defeasible inferences often add new information to our assumptions: while being explanatory of the streets being wet, the fact that it rained is not contained in the fact that the streets are wet, and while being able to fly is a typical property of birds, being a bird does not necessitate being able to fly. In this sense defeasible inferences are ampliative.
Logics that may lose conclusions once more information is acquired are called nonmonotonic. The vast majority of logics the reader will typically encounter in logic textbooks are monotonic, with classical logic (in short, CL) being the celebrity. Whenever the given assumptions are true, an inference sanctioned by CL will securely pass the torch from the assumptions to the conclusion, warranting with absolute certainty the truth of the conclusion. Truth is preserved in inferences sanctioned by CL. No matter how much information we add, how many inferences we chain between our premises and our final conclusion, or how often the torch is passed, truth endures: the flames reach their final destination. Thus, inferences are never retracted in CL, and conclusions accumulate the more assumptions we add. This property, called monotonicity, is highly desirable for certain domains of reasoning such as mathematics, a domain where CL reigns.
However, a key motivation behind the development of NML is that out in the wild of commonsense, expert, or scientific reasoning, good inferences need not be truth preservational: we often change our minds and retract inferences when watching a crime show and wondering who the most likely murderer is; medical doctors may change their diagnosis with the arrival of more evidence, and so do scientists, sometimes resulting in scientific revolutions. In less idealized circumstances than those of purely formal sciences (such as mathematics), we usually need to reason with incomplete, sometimes even conflicting information. As a consequence, our inferences allow for exceptions and/or criticism. They are adaptable: learning or inferring more information may cause retraction, previous inferences may get defeated. Outside the ivory tower of mathematics, in the stormy domain of commonsense reasoning, the torch’s fire may get extinguished.
It is therefore not surprising that examples of defeasible reasoning are abundant. In what follows, we will list some paradigmatic examples.
Example 1. We first imagine a scenario at a student party.Footnote 2

Table 001Long description
The example shows five lines of dialogue set at a student party. 1. Peter: I haven't seen Ruth!. 2. Mary: Me neither. If there's an exam the next day Ruth studies late in the library. 3. Peter: Yes, that's it. The logic exam tomorrow!. 4. Anne: But today is Sunday. Isn't the library closed question mark. 5. Peter: True, and indeed there she is, exclamation mark. [pointing to Ruth entering the room].
In her reply to Peter’s observation concerning Ruth’s absence (1), Mary states a regularity in form of a conditional (2): If there’s an exam the next day, Ruth studies late in the library. She offers an explanation as to why Ruth is not around. The explanation is hypothetical, since she doesn’t offer any insights as to whether there is an exam. Peter supplements the information that, indeed, (3) there is an exam. Were our students to treat information (2) and (3) in the manner of CL as a material implication, they would be able to apply modus ponens to infer that Ruth is currently studying late in the library.Footnote 3 And, indeed, after utterance (3) it is quite reasonable for Mary and Peter to conclude that
(⋆) Ruth is not at the party since she’s studying late at the library.
Anne’s statement (4) casts doubt on the argument (⋆), since the library might be closed today. This does not undermine the regularity stated by Mary, but it points to a possible exception. Anne’s statement may lead to the retraction of (⋆), which is further confirmed when Peter finally sees Ruth (5): this is defeasible reasoning in action!
Defaults. Statements such as “Birds fly.” allow for exceptions. It is therefore not surprising that one of the most frequent characters in papers on NML is Tweety. While the reader may sensibly infer that Tweety can fly when they are told that Tweety is a bird, they might be skeptical when being informed that Tweety lives at the South Pole, and most definitely will retract the inference as soon as they hear that Tweety is a penguin.Footnote 4 As we have also seen in our example, we often express regularities in the form of conditionals – so-called default rules, or simply defaults – that hold typically, mostly, plausibly, and so on, but not necessarily.
Closed-World Assumption. Often, defeasible reasoning is rooted in the fact that communication practices are based on an economic use of information. When making lists such as menus at restaurants or timetables at railway stations, we typically only state positive information. We interpret (and compile) such lists under the assumption that what is not listed is not the case. For instance, if a meal or connection is not listed, we consider it not to be available. This practice is called the closed-world assumption (Reiter, Reference Reiter1981).
Rules with Explicit Exceptions. Before presenting more examples of defeasible reasoning, let us halt for a moment to address a possible objection. Is CL really inadequate as a model of this kind of reasoning? Can’t we simply express all possible exceptions as additional premises? For instance,
(†) If there’s an exam the next day and the library is open late and Ruth is not ill and on her way didn’t get into a traffic jam and …, then Ruth studies late in the library.
There are several problems with this proposal. The first concerns the open-ended nature of the list of exceptions which characterizes most rules that express what typically/usually/plausibly/and so on holds. Even in the (rare) cases in which it is – in principle – possible to compile a complete list of exceptions, the resulting conditional will not adequately represent a reasoning scenario in which our agent may not be aware of all possible exceptions. They may merely be aware of the possibility of exceptions and be able, if asked for it, to list some (such as penguins as nonflying birds). Others may escape them (such as kiwis), but they would readily retract their inference that Tweety flies after learning that Tweety is a kiwi. In other words, the complexities involved in generating explicit lists of exceptions are typically far beyond the capacities of real-life and artificial agents. What is more, in order to apply modus ponens to conditionals such as (†), our reasoner would have to first check for whether each possible exception holds. This may be impossible for some, for others unfeasible, and altogether it would render out of reach the pace of reasoning that is needed to cope with their real-life situation.
In contrast to reasoning from fixed sets of axioms in mathematics, commonsense reasoning needs to cope with incomplete (and possibly conflicting) information. In order to get off the ground, it (a) jumps to conclusions based on regularities that allow for exceptions and (b) adapts to potential problems in the form of exceptional circumstances on the fly, by means of the retraction of previous inferences.
Abductive Inferences. Another type of defeasible reasoning concerns cases in which we infer explanations of a given state of affairs (also called abductive inferences). For instance, upon seeing the wet street in front of her apartment, Susie may infer that it rained, since this explains the wetness of the streets. However, when Mike informs her that the streets have been cleaned a few minutes ago, she will retract her inference. We see this kind of inference often in diagnosis and investigative reasoning (think of Sherlock Holmes or a scientist wondering how to interpret the outcome of an experiment). As both the exciting histories of the sciences and the twisted narratives of Sir Arthur Conan Doyle reveal, abductive inference is defeasible.
Inductive Generalizations. In both scientific and everyday reasoning, we frequently rely on inductive generalizations. Having seen only white swans, a child may infer that all swans are white, only to retract the inference during a walk in the park when a black swan crosses their path.
These are some central, but far from the only types of defeasible inferences. A more exhaustive and systematic overview can be found, for instance, in Walton et al. (Reference Walton, Reed and Macagno2008), where they are informally analyzed in terms of argument schemes.Footnote 5
1.2 Challenges to Models of Defeasible Reasoning
Formal models of defeasible reasoning face various challenges. Let us highlight some.
1.2.1 Human Reasoning and the Richness of Natural Language
As we have seen, defeasible reasoning is prevalent in contexts in which agents are equipped with incomplete and uncertain information. By providing models of defeasible reasoning, NMLs are of interest to both philosophers investigating the rationality underlying human reasoning and computer scientists interested in the understanding and construction of artificially intelligent agents. Human reasoning has a peculiar status in both investigations in that selected instances of it serve as role models of rational and successful artificial reasoning. After all, humans are equipped with a highly sophisticated cognitive system that has evolutionarily adapted to an environment of which it only has incomplete and uncertain information. Therefore, it seems quite reasonable to assume that we can learn a good deal about defeasible reasoning, including the question of what is good defeasible inference, by observing human inference practices.
There are, however, several complications that come with the paradigmatic status of human defeasible reasoning. First, human reasoning is error-prone, which means we have to rely on selected instances of good reasoning. But what are exemplars of good reasoning? In view of this problem, very often nonmonotonic logicians simply rely on their own intuitions. There are good reasons why one should not let expert intuition be the last word on the issue. We may be worried, for instance, about the danger of myside bias (also known as confirmation bias; see Mercier and Sperber (Reference Mercier and Sperber2011)): intuitions may be biased toward satisfying properties of the formal system that is proposed by the respective scholar.
Then, there is the possibility of “déformation professionnelle,” given that the expert’s intuitions have been fostered in the context of a set of paradigmatic examples about penguins with the name Tweety, ex-US presidents (see Examples 2 and 3), and the like.Footnote 6
Another complication is the multifaceted character of defeasible reasoning in human reasoning. First, there is the variety of ways we can express in natural language regularities that allow for exceptions. We have “Birds fly,” “Birds typically fly,” “Birds stereotypically fly,” “Most birds fly,” and so on, none of which are synonymous: for example, while tigers stereotypically live in the wild, most tigers live in captivity. What is more important, the different formulations may give rise to different permissible inferences. Consider the generic “Lions have manes.” While having a mane implies being a male lion, “Lions are males” is not acceptable (Pelletier & Elio, Reference Pelletier and Elio1997). The inference pattern blocked is known as right weakening: if ![]() by default implies
by default implies ![]() , and
, and ![]() follows classically from
follows classically from ![]() , then
, then ![]() follows by default from
follows by default from ![]() as well. It is valid in most NMLs, and it seems adequate for the “typical,” “stereotypical,” and “most” reading of default rules, but not for some generics.Footnote 7 For NMLs this poses the challenge to keep in mind the intended interpretation of defaults and differences in the underlying logical properties that various interpretations give rise to.
as well. It is valid in most NMLs, and it seems adequate for the “typical,” “stereotypical,” and “most” reading of default rules, but not for some generics.Footnote 7 For NMLs this poses the challenge to keep in mind the intended interpretation of defaults and differences in the underlying logical properties that various interpretations give rise to.
Despite these problems, it seems clear that “reasoning in the wild” should play a role in the validation and formation of NMLs.Footnote 8 This pushes NML in proximity to psychology. In practice, nonmonotonic logicians try to strike a good balance by obtaining metatheoretically well-behaved formal systems that are to some degree intuitively and descriptively adequate relative to (selected) human reasoning practices.
1.2.2 Conflicts and Consequences
Defeasible arguments frequently conflict. This poses a challenge for normative theories of defeasible reasoning, which must specify the conditions under which inferences remain permissible in such scenarios.
For this discussion, some terminology and notation will be useful. An argument (in our technical sense) is obtained by either stating basic assumptions or by applying inference rules to the conclusions of other arguments. An argument is defeasible if it contains a defeasible rule (such as a default), symbolized by ![]() . Such an argument may include also truth-preservational strict inference rules (such as the ones from CL), symbolized by
. Such an argument may include also truth-preservational strict inference rules (such as the ones from CL), symbolized by ![]() . A conflict between two arguments arises if they lead to contradictory conclusions
. A conflict between two arguments arises if they lead to contradictory conclusions ![]() and
and ![]() (where
(where ![]() denotes negation).
denotes negation).
Let us now take a look at two paradigmatic examples.
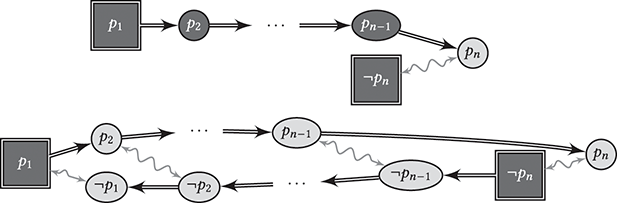
Example 2 Nixon; Reiter and Criscuolo (1981). One of the most well-known examples in NML is the Nixon Diamond (see Fig. 1):Footnote 9
- 1. Nixon is a Dove.

- 2. Nixon is a Quaker.

- 3. By default, Doves are Pacifists.

- 4. By default, Quakers are not Pacifists.

Example 3 (Tweety; Doyle and McDermott (1980)). Another well-known example is Tweety the penguin (see Fig. 2) based on the following information:
- 1. Tweety is a penguin.

- 2. Penguins are birds.

- 3. By default, birds fly.

- 4. By default, penguins don’t fly.


Figure 1 The Nixon Diamond from Example 2. Double arrows symbolize defeasible rules, single arrows strict rules, and wavy arrows conflicts. Black nodes represent unproblematic conclusions, while light nodes represent problematic conclusions. Rectangular nodes represent the starting point of the reasoning process. We use the same symbolism in the following figures.

Figure 2 Tweety and specificity, Example 3.
Figure 2Long description
A single arrow from penguin leads to bird (black node). A double arrow from penguin leads to ¬ fly (black node) and from bird leads to fly (light node). A way arrow is drawn between fly and ¬fly.
Our examples indicate that, first, conflicts between defeasible arguments can occur, and second, the context may determine whether and, if so, how a conflict can be resolved. We now take a look at two further challenges that come with conflicts in defeasible reasoning.
Figure 3 encodes the following information: ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Should we infer
. Should we infer ![]() ? Nonmonotonic logics that block this inference have been said to suffer from the drowning problem (Benferhat et al., Reference Benferhat, Cayrol, Dubois, Lang and Prade1993). Examples like the following seem to suggest that we should accept
? Nonmonotonic logics that block this inference have been said to suffer from the drowning problem (Benferhat et al., Reference Benferhat, Cayrol, Dubois, Lang and Prade1993). Examples like the following seem to suggest that we should accept ![]() .
.

Figure 3 A drowning scenario.
Example 4. We consider the scenario:
- 1. Micky is a dog.

- 2. Dogs normally (have the ability to) to tag along with a jogger.

- 3. Dogs normally (have the ability to) bark.

- 4. Micky lost a leg and can’t tag along with a jogger.

In this example it seems reasonable to infer, ![]() , Micky has the ability to bark, despite the presence of
, Micky has the ability to bark, despite the presence of ![]() . In other contexts one may be more cautious when jumping to a conclusion.
. In other contexts one may be more cautious when jumping to a conclusion.
Example 5. Take the following scenario.
- 1. It is night.

- 2. During the night, the light in the living room is usually off.

- 3. During the night, the heating in the living room is usually off.

- 4. The light in the living room is on.

In this scenario it seems less intuitive to infer, ![]() , The heating in the living room is off. The fact that we have in (4) an exception to default (2) may have an explanation in the light of which also default (3) is excepted. For example, the inhabitant forgot to check the living room before going to sleep, she is not at home and left the light and heating on before leaving, she is still in the living room, and so on.
, The heating in the living room is off. The fact that we have in (4) an exception to default (2) may have an explanation in the light of which also default (3) is excepted. For example, the inhabitant forgot to check the living room before going to sleep, she is not at home and left the light and heating on before leaving, she is still in the living room, and so on.
These examples show that concrete reasoning scenarios often contain a variety of relevant factors that influence what real-life reasoners take to be intuitive conclusions. Specific NMLs typically only model a few of these factors and omit others. For instance, although Elio and Pelletier (Reference Elio and Pelletier1994) and Koons (Reference Koons and Zalta2017) argue that it is useful to track causal and explanatory relations in the context of drowning problems, systematic research in this direction is lacking.
Another class of difficult scenarios has to do with so-called floating conclusions.Footnote 10
These are conclusions that follow from two opposing arguments. For example, formally the scenario may be as depicted in Fig. 4.

Figure 4 A scenario with the floating conclusion ![]() .
.
Example 6. Suppose two generally reliable weather reports:
- 1. Station 1: The hurricane will hit Louisiana and spare Alabama.

- 2. Station 2: The hurricane will hit Alabama and spare Louisiana.

- 3. If the hurricane hits Louisiana, it hits the South coast.

- 4. If the hurricane hits Alabama, it hits the South coast.

The floating conclusion, (5), The storm will probably hit the South coast, may seem acceptable to a cautious reasoner. The rationale being that both reports agree on the upcoming storm and even roughly where it will hit. The disagreement may be due to different weighing of diverse factors in their respective underlying scientific weather models. But the combined evidence of both stations seems to rather confirm conclusion (5) than dis-confirm it. This is not always the case with partially conflicting expert statements, as the next example shows.
Example 7. Assume two expert reviewers, Reviewer 1 and Reviewer 2, evaluating Anne for a professorship. She sent in two manuscripts, A and B.
- 1. Reviewer 1: Manuscript A is highly original, while manuscript B repeats arguments already known in the literature.

- 2. According to Reviewer 1, one manuscript is highly original.

- 3. Reviewer 2: Manuscript B is highly original, while manuscript A repeats arguments already known in the literature.

(We assume the inconsistency of
 with
with  .)
.)- 4. According to Reviewer 2, one manuscript is highly original.

Should we conclude that one manuscript is highly original, since it follows from both reviewers’ evaluations? It seems a more cautious stance is advisable. The disagreement may well be an indication of the sub-optimality of each of the two reviews. Indeed, a possible explanation of their conflicting assessments could be that (a) Reviewer 1 is aware of an earlier article ![]() (by another author than Anne) that already makes the arguments presented in
(by another author than Anne) that already makes the arguments presented in ![]() and which is not known to Reviewer 2, and vice versa, that (b) Reviewer 2 is aware of an earlier article
and which is not known to Reviewer 2, and vice versa, that (b) Reviewer 2 is aware of an earlier article ![]() in which similar arguments to those in
in which similar arguments to those in ![]() are presented. In view of this possibility, it would seem overly optimistic to infer that Anne has a highly original article in her repertoire.
are presented. In view of this possibility, it would seem overly optimistic to infer that Anne has a highly original article in her repertoire.
2 Central Concepts
Nonmonotonic logics are designed to answer the question what are (defeasible) consequences of some available set of information. This gives rise to the notion of a nonmonotonic consequence relation. In this section we explain this central concept and some of its properties from an abstract perspective (Section 2.2). Nonmonotonic consequences are obtained by means of defeasible inferences, which are themselves obtained by applying inference rules. We discuss two ways of formalizing such rules in Section 2.3. Before doing so, we discuss some basic notation in Section 2.1.
2.1 Notation and Basic Formal Concepts
Let us get more formal. We assume that sentences are expressed in a (formal) language ![]() . We denote the standard connectives in the usual way:
. We denote the standard connectives in the usual way: ![]() (negation),
(negation), ![]() (conjunction),
(conjunction), ![]() (disjunction),
(disjunction), ![]() (implication), and
(implication), and ![]() (equivalence). We use lowercase letters
(equivalence). We use lowercase letters ![]() as propositional atoms, collected in the set
as propositional atoms, collected in the set ![]() , and uppercase letters
, and uppercase letters ![]() as metavariables for sentences such as
as metavariables for sentences such as ![]() ,
, ![]() or
or ![]() . We denote the set of sentences underlying
. We denote the set of sentences underlying ![]() by
by ![]() . In the context of classical propositional logic and typically in the context of a Tarski logic (see later), this will simply be the closure of the atoms under the standard connectives.Footnote 11 We denote sets of sentences by the uppercase calligraphic letters
. In the context of classical propositional logic and typically in the context of a Tarski logic (see later), this will simply be the closure of the atoms under the standard connectives.Footnote 11 We denote sets of sentences by the uppercase calligraphic letters ![]() ,
, ![]() , and
, and ![]() . Where
. Where ![]() is a finite nonempty set of sentences, we write
is a finite nonempty set of sentences, we write ![]() and
and ![]() for the conjunction resp. the disjunction over the elements of
for the conjunction resp. the disjunction over the elements of ![]() .Footnote 12
.Footnote 12
A consequence relation, denoted by ![]() , is a relation
, is a relation ![]() between sets of sentences and sentences:
between sets of sentences and sentences: ![]() denotes that
denotes that ![]() is a
is a ![]() -consequence of the assumption set
-consequence of the assumption set ![]() . So, the right side of
. So, the right side of ![]() encodes the given information resp. the assumptions on which the reasoning process is based, while the left side encodes the consequences which are sanctioned by
encodes the given information resp. the assumptions on which the reasoning process is based, while the left side encodes the consequences which are sanctioned by ![]() given
given ![]() .
.
We will often work in the context of Tarski logics ![]() , whose consequence relations
, whose consequence relations ![]() are reflexive (
are reflexive (![]() ), transitive (
), transitive (![]() and
and ![]() implies
implies ![]() ) and monotonic (Definition 2.1). We will also assume compactness (if
) and monotonic (Definition 2.1). We will also assume compactness (if ![]() then there is a finite
then there is a finite ![]() for which
for which ![]() ). The most well-known Tarski logic is, of course, classical logic
). The most well-known Tarski logic is, of course, classical logic ![]() .
.
2.2 An Abstract View on Nonmonotonic Consequence
The following definition introduces one of our key concepts: nonmonotonic consequence relations.
Definition 2.1. A consequence relation ![]() is monotonic iff (“if and only if”) for all sets of sentences
is monotonic iff (“if and only if”) for all sets of sentences ![]() and
and ![]() and every sentence
and every sentence ![]() it holds that
it holds that ![]() if
if ![]() . It is nonmonotonic iff it is not monotonic.
. It is nonmonotonic iff it is not monotonic.
We use ![]() as a placeholder for nonmonotonic consequence relations. Our definition expresses that for nonmonotonic consequence relations
as a placeholder for nonmonotonic consequence relations. Our definition expresses that for nonmonotonic consequence relations ![]() there are sets of sentences
there are sets of sentences ![]() and
and ![]() for which
for which ![]() while
while ![]() (i.e.,
(i.e., ![]() is not a
is not a ![]() -consequence of
-consequence of ![]() ).
).
In the following we will introduce some properties that are often discussed as desiderata for nonmonotonic consequence relations.Footnote 13 A positive account of what kind of logical behavior to expect from these relations is particularly important given the fact that ‘nonmonotonicity’ only expresses a negative property. This immediately raises the question whether there are restricted forms of monotonicity that one would expect to hold even in the context of defeasible reasoning? One proposal is
- Cautious Monotonicity (CM).
 , if
, if  and
and  .Footnote 14
.Footnote 14
Whereas nonmonotonicity expresses that adding new information to one’s assumptions may lead to the retraction resp. the defeat of previously inferred conclusions, CM states that some type of information is safe to add: namely, adding a previously inferred conclusion does not lead to the loss of conclusions.
We sketch the underlying rationale. Suppose ![]() and
and ![]() . In view of
. In view of ![]() , the defeasible consequence
, the defeasible consequence ![]() of
of ![]() is sanctioned. So,
is sanctioned. So, ![]() does not contain defeating information for concluding
does not contain defeating information for concluding ![]() . Now, the only reason for
. Now, the only reason for ![]() would be that the addition of
would be that the addition of ![]() to
to ![]() generates defeating information for concluding
generates defeating information for concluding ![]() . However,
. However, ![]() already followed from
already followed from ![]() , since
, since ![]() . Thus, this defeating information should have already been contained in
. Thus, this defeating information should have already been contained in ![]() , before adding
, before adding ![]() . But then
. But then ![]() , a contradiction.
, a contradiction.
One may also demand that adding ![]() -consequences to an assumption set should not lead to more consequences.
-consequences to an assumption set should not lead to more consequences.
- Cautious Transitivity (CT).
 , if
, if  and
and  .
.
Combining CM and CT comes down to requiring that ![]() is robust under adding its own conclusions to the set of assumptions.
is robust under adding its own conclusions to the set of assumptions.
- Cumulativity (C).
If
 , then
, then  iff
iff  .
.
Instead of considering the dynamics of consequence under additions of new assumptions, one may wonder what happens when assumptions are manipulated. For instance, it seems desirable that a consequence relation is robust under substituting assumptions for equivalent ones.
- Left Logical Equivalence (LLE).
Where
 and
and  are classically equivalent sets,Footnote 15
are classically equivalent sets,Footnote 15  iff
iff  .
.
Note that in the context of nonmonotonic consequence it would be too strong to require
- Left Logical Strengthening (LLS).
Where
 ,
,  implies
implies  .
.
In order to see why LLS is undesirable, consider an example featuring Tweety. If it is only known that Tweety is a bird, it nonmonotonically follows that it can fly, ![]() . The situation changes when it is also known that Tweety is a penguin,
. The situation changes when it is also known that Tweety is a penguin, ![]() .
.
For the right-hand side of ![]() one may also expect a property similar to LLE: if
one may also expect a property similar to LLE: if ![]() is a consequence, so is each equivalent formula
is a consequence, so is each equivalent formula ![]() . The following principle is stronger. It is motivated by the truth-preservational nature of CL-inferences (but recall from Section 1.2 that in the context of generics it may be problematic):
. The following principle is stronger. It is motivated by the truth-preservational nature of CL-inferences (but recall from Section 1.2 that in the context of generics it may be problematic):
- Right Weakening (RW).
Where
 ,
,  implies
implies  .
.
Finally, if we take our assumptions to express certain information (rather than defeasible assumptions, see Section 4), then one may expect
- Reflexivity (Ref).
 .
.
Consequence relations that satisfy RW, LLE, Ref, CT, and CM are called cumulative consequence relations (Kraus et al., Reference Kraus, Lehman and Magidor1990).Footnote 16 The authors consider them “the rockbottom properties without which a system should not be considered a logical system.” (p. 176), a point mirroring Gabbay (Reference Gabbay and Apt1985). Some other intuitive principles hold for a cumulative ![]() .
.
Proposition 2.1. Every cumulative consequence relation ![]() also satisfies:
also satisfies:
1. Equivalence. If
 and
and  then:
then:  iff
iff  .
.2. AND. If
 and
and  then
then  .
.
Proof. Item 1 follows by CT and CM. To see this suppose (a) ![]() , (b)
, (b) ![]() , and (c)
, and (c) ![]() . We show
. We show ![]() (the inverse direction is analogous). By CM, (a) and (c),
(the inverse direction is analogous). By CM, (a) and (c), ![]() . Thus, by CT and (b),
. Thus, by CT and (b), ![]() .
.
Ad 2. Suppose (a) ![]() and (b)
and (b) ![]() . By Ref,
. By Ref, ![]() and by LLE, (c),
and by LLE, (c), ![]() . By CM, (a) and (b),
. By CM, (a) and (b), ![]() . By CT and (c),
. By CT and (c), ![]() . By (a) and CT,
. By (a) and CT, ![]() . □
. □
Another property of some NMLs is constructive dilemma: given a fixed context represented by ![]() , if
, if ![]() is both a consequence of
is both a consequence of ![]() and of
and of ![]() , it should also be a consequence of
, it should also be a consequence of ![]() .
.
- Constructive Dilemma (OR)
If
 and
and  then
then  .
.
Cumulative consequence relations that also satisfy OR are called preferential (Kraus et al., Reference Kraus, Lehman and Magidor1990). We show some derived principles for preferential consequence relations.
Proposition 2.2. Every preferential consequence relation ![]() also satisfies:
also satisfies:
1. Reasoning by Cases (RbC). If
 and
and  then
then  .
.2. Resolution. If
 then
then  .
.
Proof. (RbC). Suppose ![]() and
and ![]() . By OR,
. By OR, ![]() and by LLE,
and by LLE, ![]() . (Resolution). Suppose now that
. (Resolution). Suppose now that ![]() . By RW, (a),
. By RW, (a), ![]() . By Ref,
. By Ref, ![]() and by RW, (b),
and by RW, (b), ![]() . By RbC, (a) and (b),
. By RbC, (a) and (b), ![]() . □
. □
A more controversial property than CM is rational monotonicity (RM).Footnote 17 The basic intuition is similar to CM: given an assumption set ![]() , we are interested in securing a safe set of sentences under the addition of which
, we are interested in securing a safe set of sentences under the addition of which ![]() is monotonic. While for CM this was the set of the
is monotonic. While for CM this was the set of the ![]() -consequences of
-consequences of ![]() , RM considers the set of all sentences that are consistent with the consequences of
, RM considers the set of all sentences that are consistent with the consequences of ![]() (consistent in the sense that their negation is not a
(consistent in the sense that their negation is not a ![]() -consequence of
-consequence of ![]() ).
).
- Rational Monotonicity (RM)
 , if
, if  and
and  .
.
One way to think about RM is as follows. Let us (i) say that ![]() is defeating information for
is defeating information for ![]() if there is an
if there is an ![]() for which
for which ![]() , while
, while ![]() , and (ii)
, and (ii) ![]() is rebutted by
is rebutted by ![]() in case
in case ![]() .Footnote 18 Then, when putting CM and RM in contrapositive form,
.Footnote 18 Then, when putting CM and RM in contrapositive form,
CM expresses that no defeating information for
 is derivable from any
is derivable from any  : formally, if
: formally, if  and
and  then
then  ;
;RM expresses the stronger demand that every defeating information for
 is rebutted by
is rebutted by  : formally, if
: formally, if  and
and  then
then  .
.
So, RM requires that reasoners take into account potentially defeating information by having rebutting counterarguments at hand. This is quite demanding, since, as we have discussed in Section 1, (a) the reasoner may not be aware of all possibly rebutting information to her previous inferences and (b) it may be counterintuitive to conclude that each and every possible defeater is false.
Poole (Reference Poole1991) points out another problem. Consider the statement that Tweety is a bird. Now, all bird species are exceptional to some defaults about birds: penguins don’t fly, hummingbirds have an unusual size, sandpipers nest on the ground, and so on. But, then RM requires us to infer that Tweety is not a penguin, not a hummingbird, not a sandpiper, and so on, and therefore does not belong to any bird species.
In this section we have seen various properties of nonmonotonic consequence relations, many of which are considered desiderata by nonmonotonic logicians. Their study is therefore of central interest in NML and we will come back to them in the context of many of the methods presented in this Element.
2.3 Plausible and Defeasible Reasoning
A fundamental question underlying the design of NMLs is whether to model defeasible reasoning
1. by means of classical inferences based on defeasible assumptions, or
2. by means of (genuinely) defeasible inference rules.
The former is sometimes called Plausible Reasoning, the latter Defeasible Reasoning.Footnote 19 Table 1 provides an overview on which of the two reasoning styles is modeled by various NMLs discussed in this Element. We illustrate with an abstract example. Suppose we want to model that
 defeasibly implies
defeasibly implies  , and that
, and that defeasibly implies
defeasibly implies  .
.
In the first approach we encode these two defeasible regularities in terms of classical implications. It can be realized in two ways.
Plausible Reasoning via abnormality assumptions. One way is by formalizing the defeasible rules by
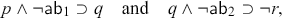
where ![]() and
and ![]() are atomic sentences that encode exceptional circumstances, that is, abnormalities, for the respective rules. These abnormalities are assumed to be false, by default. Suppose that
are atomic sentences that encode exceptional circumstances, that is, abnormalities, for the respective rules. These abnormalities are assumed to be false, by default. Suppose that ![]() is true. Then, by also assuming the falsity of
is true. Then, by also assuming the falsity of ![]() and
and ![]() we can apply modus ponens to both material implications and conclude
we can apply modus ponens to both material implications and conclude ![]() .
.

Table 1Long description
The table consists of four columns: NML, Defeasible Reasoning, Plausible Reasoning, and Blank. It read as follows. Row 1: ASPIC plus; checkmark in Defeasible Reasoning; checkmark in Plausible Reasoning; Section 8. Row 2: Logic-based argumentation; checkmark in Plausible Reasoning; Section 9. Row 3: Rescher and Manor; checkmark in Plausible Reasoning; Section 11 dot 3 dot 1. Row 4: Default Assumptions; checkmark in Plausible Reasoning; Section 11 dot 3 dot 1. Row 5: Adaptive Logic; checkmark in Plausible Reasoning; Section 11 dor 3 dot 1. Row 6: Input-Output Logic; checkmark in Defeasible Reasoning; checkmark in Plausible Reasoning with asterisk; Section 11 dot 3 dot 2. Row 7: Reiter Default Logic; checkmark in Defeasible Reasoning; checkmark in Plausible Reasoning with asterisk; Section 12. Row 8: Logic Programming; checkmark in Plausible Reasoning; Section 16.
Let us see how retraction works in this approach by supposing ![]() . In this case we can classically derive
. In this case we can classically derive ![]() , but neither
, but neither ![]() nor
nor ![]() . Note that contraposition of defeasible rules is available in this approach. For instance,
. Note that contraposition of defeasible rules is available in this approach. For instance, ![]() is CL-equivalent to
is CL-equivalent to ![]() .Footnote 20 So, we know (at least) one of the assumptions must be false, but we don’t know which. Absent any other reason to prefer one over the other, we can’t rely on
.Footnote 20 So, we know (at least) one of the assumptions must be false, but we don’t know which. Absent any other reason to prefer one over the other, we can’t rely on ![]() to derive
to derive ![]() . In view of this,
. In view of this, ![]() should not be considered a nonmonotonic consequence of the given information.
should not be considered a nonmonotonic consequence of the given information.
Plausible Reasoning via naming of defaults. Another way to proceed is by naming defaults (see, e.g., Poole (Reference Poole1988)). Here, we make use of defeasible assumptions ![]() and
and ![]() , which name defeasible inference rules and which are assumed to be true, by default. In our example, we add
, which name defeasible inference rules and which are assumed to be true, by default. In our example, we add

to the (nondefeasible) assumptions. Note that ![]() (resp.
(resp. ![]() ) is classically equivalent to
) is classically equivalent to ![]() (resp.
(resp. ![]() ). So, when substituting
). So, when substituting ![]() for
for ![]() and
and ![]() for
for ![]() the approach based on naming defaults and the approach based on abnormality assumptions boil down to the same.
the approach based on naming defaults and the approach based on abnormality assumptions boil down to the same.
Defeasible Reasoning. In this approach, regularities are expressed as genuinely defeasible rules (written with ![]() ), that is, without additional and explicit defeasible assumptions that are part of the antecedent of the rule. We encode our preceding example by
), that is, without additional and explicit defeasible assumptions that are part of the antecedent of the rule. We encode our preceding example by

Note that ![]() is not classical implication, in particular
is not classical implication, in particular ![]() does, in general, not follow from
does, in general, not follow from ![]() in this approach. In the first scenario, where only
in this approach. In the first scenario, where only ![]() is given, we apply a defeasible modus ponens rule to obtain
is given, we apply a defeasible modus ponens rule to obtain ![]() and then again to obtain
and then again to obtain ![]() . Many NMLs implement a greedy style of reasoning, according to which defeasible modus ponens is applied as much as possible. Now, if
. Many NMLs implement a greedy style of reasoning, according to which defeasible modus ponens is applied as much as possible. Now, if ![]() is also part of the assumptions, we derive
is also part of the assumptions, we derive ![]() from
from ![]() and
and ![]() , but then stop, since inferring
, but then stop, since inferring ![]() from
from ![]() and
and ![]() would result in inconsistency.
would result in inconsistency.
Example 8. For a more general context, we consider an example with defaults ![]() and the (certain) information
and the (certain) information ![]() and
and ![]() depicted in Figure 5. In the greedy style of reasoning underlying Defeasible Reasoning we will be able to apply defeasible modus ponens to derive
depicted in Figure 5. In the greedy style of reasoning underlying Defeasible Reasoning we will be able to apply defeasible modus ponens to derive ![]() ,
, ![]() , …,
, …, ![]() . Only the last application resulting in
. Only the last application resulting in ![]() is blocked by the defeating information
is blocked by the defeating information ![]() . The situation is different for Plausible Reasoning. Since contraposition is available, for each argument
. The situation is different for Plausible Reasoning. Since contraposition is available, for each argument ![]() (where each
(where each ![]() is modeled by
is modeled by ![]() ) there is a defeating argument
) there is a defeating argument ![]() . Altogether, we obtain
. Altogether, we obtain

This means that at least one ![]() cannot be assumed to be false, but we don’t know which one. Thus, no
cannot be assumed to be false, but we don’t know which one. Thus, no ![]() (for
(for ![]() ) is derivable according to Plausible Reasoning.
) is derivable according to Plausible Reasoning.

Figure 5 Top: Defeasible Reasoning giving rise to a greedy reasoning style. Bottom: Plausible Reasoning giving rise to contrapositions of defeasible rules.
3 From Knowledge Bases to Consequences and NMLs
Nonmonotonic logics represent the information relevant for the reasoning process (knowledge representation) and determine what follows defeasibly from the given information (nonmonotonic consequence, see Fig. 6).

Figure 6 The workings of NMLs.
The task of knowledge representation concerns, for instance, the structuring of the starting point of defeasible reasoning processes in terms of knowledge bases (Section 4) in which different types of information are distinguished, such as different types of assumptions and inference rules. Another task is to organize the given information in a way that is conducive of determining its defeasible consequences. As we have seen, this is challenging since the given information may give rise to conflicts and inconsistencies. NMLs provide methods for generating coherent chunks of information. We will highlight several ways of doing so, most roughly distinguished into syntactic and semantic approaches. The following three concepts play essential roles in the ways knowledge is represented in these approaches:Footnote 21
- Extensions
In syntactic approaches, coherent units of information are typically called extensions. What exactly extensions are differs in various NMLs. They may, for example, be sets of defeasible information from the knowledge base, sets of arguments (given a underlying notion of argument), or sets of sentences. In Section 5.1, 5.2 we will introduce two major families of syntactic approaches: argumentation and consistent accumulation. In Parts II and III they will be studied in more detail.
- Arguments
In syntactic approaches, arguments (or proofs) play a central role when building extensions. Arguments are obtained by applications of the given inference rules to the assumptions provided in the knowledge base.
- Models
In semantic approaches the focus is on classes of models provided by a given base logic. In Section 5.3 we will introduce semantic approaches and study some of them in more detail in Part IV.
The attentive reader will have noticed that we did not yet define what exactly NMLs are. In the narrow sense, one may consider them as nonmonotonic consequence relations (see Section 2.2), so a theory of what sentences follow defeasibly in the context of some knowledge base. In the wider sense they are methods for both knowledge representation and for providing nonmonotonic consequence relation(s).
In this Element we minimally assume that every NML ![]() comes with a formal language
comes with a formal language ![]() including a notion of what counts as a formula or sentence (written
including a notion of what counts as a formula or sentence (written ![]() ), an associated class of knowledge bases
), an associated class of knowledge bases ![]() (see Section 4 for details), at least one consequence relation and one of the following two:
(see Section 4 for details), at least one consequence relation and one of the following two:
in syntactic approaches: a notion of (in)consistent sets of sentences, of argument or proof, and a method to generate extensions (see Sections 5.1 and 5.2 and Parts II and III);
in semantic approaches: a notion of model and a method to select models (see Section 5.3 and Part IV).
4 Defeasible Knowledge Bases
Reasoning never starts in a void but it is initiated in a given context. For instance, some information will be factually given and some assumptions may hold by default. Moreover, when we reason we make use of inference rules. Some of these may be truth-preservational (such as the rules provided by ![]() ), others defeasible, allowing for exceptional circumstances. Defeasible knowledge bases structure reasoning contexts into different types of constituents, such as different types of assumptions and inference rules. Most broadly conceived they are tuples of the form:
), others defeasible, allowing for exceptional circumstances. Defeasible knowledge bases structure reasoning contexts into different types of constituents, such as different types of assumptions and inference rules. Most broadly conceived they are tuples of the form:
 (4.0.1)
(4.0.1)
We let ![]() be the defeasible part of
be the defeasible part of ![]() consisting of its defeasible assumptions and rules.
consisting of its defeasible assumptions and rules.
A concrete ![]() has an associated fixed class of knowledge bases
has an associated fixed class of knowledge bases ![]() . Its underlying consequence relation(s)
. Its underlying consequence relation(s) ![]() are relations between
are relations between ![]() and
and ![]() .Footnote 22
.Footnote 22
In concrete NMLs, usually not all components of (4.0.1) are utilized or explicitly listed. For example, some NMLs do not consider defeasible rules, some come without defeasible assumptions, some without priorities, many without metarules. Take, for instance, NMLs that model Plausible Reasoning. Here, we omit ![]() since such NMLs do not work with defeasible rules. Moreover, specific components of the knowledge base are fixed for many NMLs, or they are constrained. For instance, only specific preferences relations
since such NMLs do not work with defeasible rules. Moreover, specific components of the knowledge base are fixed for many NMLs, or they are constrained. For instance, only specific preferences relations ![]() may be allowed for, such as transitive ones. Or, often the strict rules are induced by classical logic. (In such cases, the strict rules are often omitted from
may be allowed for, such as transitive ones. Or, often the strict rules are induced by classical logic. (In such cases, the strict rules are often omitted from ![]() .) In some NMLs the strict rules vary over different applications (e.g., in logic programming where strict rules usually represent domain-specific knowledge such as “penguins are birds”). In Table 2 we provide an overview for NMLs presented in this Element.
.) In some NMLs the strict rules vary over different applications (e.g., in logic programming where strict rules usually represent domain-specific knowledge such as “penguins are birds”). In Table 2 we provide an overview for NMLs presented in this Element.

Table 2Long description
The table with seven columns titled: NML, A subscript s, A subscript d, R subscript s, R subscript d, R subscript m, and Section. The rows read as follows: Row 1: ASPIC plus, tick in A subscript s, A subscript d, R subscript s, and R subscript d; Section 8. Row 2: Logic-based argumentation, tick in A subscript s and A subscript d, tick with R subscript L in R subscript s; Section 9. Row 3: Rescher and Manor: tick in A subscript d, tick in R subscript CL in R subscript s; Section 11 dot 3 dot 1. Row 4: Default Assumptions, tick in A subscript s and A subscript d, tick with R subscript CL in R subscript s; Section 11 dot 3 dot 1. Row 5: Input-output logics, tick in A subscript s, tick with R subscript CL in R subscript s; tick in R subscript d and tick mark in R subscript m; Section 11 dot 3 dot 2. Row 6: Reiter Default Logic, tick in A subscript s, tick with R subscript CL in R subscript s, tick in R subscript d; Section 12. Row 7: Logic Programming, tick in R subscript s; Section 16.
We now explain in more detail the components of ![]() .
.
- Strict assumptions
 is a set of sentences expressing information that is taken as indisputable or certain.
is a set of sentences expressing information that is taken as indisputable or certain.- Defeasible assumptions
 is a set of sentences that are assumed to hold normally/typically/and so on but which may be retracted in case of conflicts.
is a set of sentences that are assumed to hold normally/typically/and so on but which may be retracted in case of conflicts.- Strict rules
 is a set of truth-preservational inference rules or relations, written
is a set of truth-preservational inference rules or relations, written  .Footnote 23 There are two types of such rules. On the one hand, we have material inferences, such as “If it is a penguin, it is a bird” which may be encoded by
.Footnote 23 There are two types of such rules. On the one hand, we have material inferences, such as “If it is a penguin, it is a bird” which may be encoded by  . On the other hand, we have inferences that are valid with respect to an underlying logic
. On the other hand, we have inferences that are valid with respect to an underlying logic  , such as classical logic. If such inferences are considered, we let
, such as classical logic. If such inferences are considered, we let  if
if  . If
. If  consist exclusively of such rules, we say that it is induced by the logic
consist exclusively of such rules, we say that it is induced by the logic  and write
and write  for the set containing them. All logics
for the set containing them. All logics  considered in this Element will be Tarski logics. If
considered in this Element will be Tarski logics. If  is induced by a logic (with an implication
is induced by a logic (with an implication  ) one may model the former class of material inferences simply by means of
) one may model the former class of material inferences simply by means of  . For example, in our example one may add
. For example, in our example one may add  to the strict assumptions
to the strict assumptions  . Sometimes we find strict assumptions
. Sometimes we find strict assumptions  being modeled as strict rules with empty bodies
being modeled as strict rules with empty bodies  .
.Given a set of strict rules
 and a set of sentences
and a set of sentences  , we write
, we write  to indicate that there is a deduction of
to indicate that there is a deduction of  based on
based on  and
and  . This means that there is a sequence
. This means that there is a sequence  where
where  and for each
and for each  (with
(with  ), either
), either  or there are
or there are  for which
for which  .
.- Defeasible rules
 is a set of defeasible inference rules written
is a set of defeasible inference rules written  , often just called defaults. As discussed in Section 2.3, defeasible rules are sometimes “indirectly” modeled as strict rules with defeasible assumptions. In NMLs that adopt this method of Plausible Reasoning,
, often just called defaults. As discussed in Section 2.3, defeasible rules are sometimes “indirectly” modeled as strict rules with defeasible assumptions. In NMLs that adopt this method of Plausible Reasoning,  may be empty. In such cases we are typically dealing with a logic-induced set of strict rules
may be empty. In such cases we are typically dealing with a logic-induced set of strict rules  and defaults are sentences of the type
and defaults are sentences of the type  in
in  where
where  . Defeasible assumptions
. Defeasible assumptions  may be also considered as defaults
may be also considered as defaults  with empty bodies.
with empty bodies.
For reasons of simplicity and following the tradition of many central NMLs, we do not consider ![]() as a defeasible conditional operator in the object language
as a defeasible conditional operator in the object language ![]() , that is, an operator that can be nested within Boolean connectives. Rather, we model
, that is, an operator that can be nested within Boolean connectives. Rather, we model ![]() as representing a defeasible rule that prima facie justifies detaching
as representing a defeasible rule that prima facie justifies detaching ![]() , given
, given ![]() . However, it should be noted that this does impose a limitation on our expressive capabilities. For instance, we cannot “directly” express canceling in the context of specificity, such as
. However, it should be noted that this does impose a limitation on our expressive capabilities. For instance, we cannot “directly” express canceling in the context of specificity, such as ![]() . Many systems have been developed to overcome this limitation, such as Delgrande (Reference Delgrande1987) or conditional logics of normality (Boutilier, Reference Boutilier1994a).Footnote 24
. Many systems have been developed to overcome this limitation, such as Delgrande (Reference Delgrande1987) or conditional logics of normality (Boutilier, Reference Boutilier1994a).Footnote 24
Example 9. In Section 2.3 we presented two ways to model a scenario in which ![]() defeasibly implies
defeasibly implies ![]() and
and ![]() defeasibly imply
defeasibly imply ![]() . Suppose now additionally that
. Suppose now additionally that ![]() and
and ![]() both strictly imply
both strictly imply ![]() and that
and that ![]() defeasibly implies
defeasibly implies ![]() .
.
In Defeasible Reasoning we may work with the knowledge base ![]() consisting of
consisting of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Alternatively, one may use the strict assumptions
. Alternatively, one may use the strict assumptions ![]() and
and ![]() and
and ![]() as strict rules.
as strict rules.
In Plausible Reasoning we may utilize ![]() , where
, where ![]() and
and ![]() .
.
- Metarules
 is a set of metarules, written
is a set of metarules, written  (where
(where  are strict and defeasible rules and
are strict and defeasible rules and  is a defeasible rule) that allow one to infer new defeasible rules from those in
is a defeasible rule) that allow one to infer new defeasible rules from those in  and
and  . For example, metarules implementing reasoning-by-cases and right weakening are:
. For example, metarules implementing reasoning-by-cases and right weakening are:- OR

- RW

Given a set
 , we write
, we write  for the set of defeasible rules that are
for the set of defeasible rules that are  -deducible from
-deducible from  by the metarules in
by the metarules in  (where deductions are defined as in the context of the strict rules
(where deductions are defined as in the context of the strict rules  ).Footnote 25
).Footnote 25- Preferences
 is an order on the defeasible elements
is an order on the defeasible elements  of
of  . It encodes that some sources of defeasible information may be more reliable or have more authority than others. This information can be utilized for the purpose of resolving conflicts between defeasible arguments of different strengths. Typically
. It encodes that some sources of defeasible information may be more reliable or have more authority than others. This information can be utilized for the purpose of resolving conflicts between defeasible arguments of different strengths. Typically  is reflexive and transitive, but it may allow for incomparabilities and for equally strong but different defeasible elements. We write
is reflexive and transitive, but it may allow for incomparabilities and for equally strong but different defeasible elements. We write  for the strict version of
for the strict version of  , that is,
, that is,  iff
iff  and
and  .
.
Example 10.
Consider ![]() with
with ![]() and
and ![]() . There is a conflict between the arguments
. There is a conflict between the arguments ![]() and
and ![]() . Absent priorities, there is no way to resolve the conflict on the basis of
. Absent priorities, there is no way to resolve the conflict on the basis of ![]() . If we enhance
. If we enhance ![]() to
to ![]() where
where ![]() it seems reasonable to resolve the conflict in favor of
it seems reasonable to resolve the conflict in favor of ![]() .
.
The situation can get more involved, as the following example shows.
Example 11 (Example 9 cont.). We may extend our knowledge base to ![]() by adding the preference order:
by adding the preference order: ![]() (assuming transitivity).Footnote 26 In this case we have two conflicting arguments,
(assuming transitivity).Footnote 26 In this case we have two conflicting arguments, ![]() and
and ![]() . Comparing their strengths is no longer straightforward, since the former involves both a stronger and a weaker default than the latter. In Part III (Examples 28 and 29) we will see that different methods give rise to different conclusions for
. Comparing their strengths is no longer straightforward, since the former involves both a stronger and a weaker default than the latter. In Part III (Examples 28 and 29) we will see that different methods give rise to different conclusions for ![]() (see also Liao et al. (Reference Liao, Oren, van der Torre, Villata, Cariani, Grossi, Meheus and Parent2016)).
(see also Liao et al. (Reference Liao, Oren, van der Torre, Villata, Cariani, Grossi, Meheus and Parent2016)).
5 Methodologies for Nonmonotonic Logics
We now introduce three central methodologies to obtain nonmonotonic consequence relations and to represent defeasible knowledge, namely: formal argumentation (Section 5.1), consistent accumulation (Section 5.2), and semantic methods (Section 5.3). In this part we explain basic ideas underlying each method based on simplified settings (e.g., without metarules and preferences). More details are presented in the dedicated Parts II to IV.
5.1 The Argumentation Method
The possibility of inconsistency complicates the question as to what follows from a knowledge base ![]() . As described earlier, the idea is to generate coherent sets of information from
. As described earlier, the idea is to generate coherent sets of information from ![]() and to reason on the basis of these. For this, arguments and attacks between them play a key role. Arguments are obtained from
and to reason on the basis of these. For this, arguments and attacks between them play a key role. Arguments are obtained from ![]() by chaining strict and defeasible inference rules. We can define the set of arguments
by chaining strict and defeasible inference rules. We can define the set of arguments ![]() induced by
induced by ![]() , their conclusions, subarguments, and defeasible elements (written
, their conclusions, subarguments, and defeasible elements (written ![]() ,
, ![]() , resp.
, resp. ![]() for some
for some ![]() ) in a bottom-up way.Footnote 27
) in a bottom-up way.Footnote 27
Definition 5.1 (Arguments). Where ![]() is a knowledge base we let
is a knowledge base we let ![]() iff
iff
 , where
, where  .
.We let
 ,
,  ,
,  ,
,  .
. where
where  ,
,  and
and  is a rule in
is a rule in  .
.We let
 ,
,  ,
,  ,
,  .
.
Where ![]() we let
we let ![]() . Where
. Where ![]() , we let
, we let ![]() be the set of all
be the set of all ![]() for which
for which ![]() .
.
Example 12 (Example 9 cont.). Given our knowledge base ![]() in Example 9 we obtain the arguments depicted in Fig. 7 (left). We have, for instance,
in Example 9 we obtain the arguments depicted in Fig. 7 (left). We have, for instance, ![]() ,
, ![]() , and
, and ![]() .
.

Figure 7 The arguments and the argumentation framework for Example 13 (omitting the nonattacked and nonattacking ![]() and
and ![]() ). We explain the shading in Example 14.
). We explain the shading in Example 14.
There are many ways to define argumentative attacks and subtlety is required to avoid problems with consistency in the context of selecting arguments. We will go into more details in Part II. For now we simply suppose there to be a relation ![]() that determines when two arguments attack each other. We end up with a directed graph
that determines when two arguments attack each other. We end up with a directed graph ![]() , a so-called argumentation framework (Dung, Reference Dung1995).
, a so-called argumentation framework (Dung, Reference Dung1995).
Example 13 (Example 12 cont.). One way to define attacks in our example is to let ![]() attack
attack ![]() if for some
if for some ![]() of the form
of the form ![]() ,
, ![]() or
or ![]() . For instance,
. For instance, ![]() and
and ![]() attack each other. In Fig. 7 (right) we find the underlying argumentation framework.
attack each other. In Fig. 7 (right) we find the underlying argumentation framework.
Argumentation frameworks allow us to select coherent sets of arguments ![]() , which we will call A-extensions (for argumentative extensions). The latter represent argumentative stances of rational reasoners equipped with the knowledge base
, which we will call A-extensions (for argumentative extensions). The latter represent argumentative stances of rational reasoners equipped with the knowledge base ![]() . For this we utilize a number of constraints which represent rational desiderata on these stances. Two such desiderata on sets of arguments
. For this we utilize a number of constraints which represent rational desiderata on these stances. Two such desiderata on sets of arguments ![]() are, for instance (we refer to Part II for a more comprehensive overview):
are, for instance (we refer to Part II for a more comprehensive overview):
- Conflict-freeness:
avoid argumentative conflicts, that is, for all
 ,
,  ; and
; and- Stability:
additionally, be able to attack arguments that you don’t commit to, that is, for all
 there is an
there is an  for which
for which  .
.
Such sets of constraints give rise to so-called argumentation semantics which determine A-extensions of a given argumentation framework (Dung, Reference Dung1995). For instance, according to the stable semantics the set of A-extensions is the set of all sets of arguments that satisfy stability. Once we have settled for an argumentation semantics ![]() (such as the stable semantics) we denote the set of A-extensions of
(such as the stable semantics) we denote the set of A-extensions of ![]() relative to
relative to ![]() by
by ![]() .
.
Example 14 (Example 13 cont.). We have two stable A-extensions, that is, sets of arguments that satisfy the stability requirement (see the shaded sets in the argumentation framework of Fig. 7):

Suppose we select an A-extension ![]() . We then commit to all of the conclusions of the arguments in
. We then commit to all of the conclusions of the arguments in ![]() , that is, to
, that is, to ![]() , where
, where ![]() . This induces another notion of extension, which we dub P-extensions (propositional extensions) which are sets of conclusions associated with A-extensions. We write
. This induces another notion of extension, which we dub P-extensions (propositional extensions) which are sets of conclusions associated with A-extensions. We write ![]() for the set of P-extensions of
for the set of P-extensions of ![]() (relative to a given argumentation semantics
(relative to a given argumentation semantics ![]() ).
).
Example 15 (Example 14 cont.). The following P-extensions are associated with our A-extensions:

Once an argumentation semantics is fixed and the A- and corresponding P-extensions are generated, we can define three different consequence relations for two underlying reasoning styles (see Fig. 8): skeptical and credulous reasoning.

Figure 8 The skeptical and the credulous reasoning style.
Figure 8Long description
The diagram depicts the following: Defeasible knowledge base leads to build extensions which further leads to 1. Sceptical approach: infer A if it is supported in every extension and 2. Credulous approach: infer A if it is supported in some extension by some argument |~ ∪Ext. Sceptical approach further leads to 1. by some argument (conclusion-focused) |~ ∩PExt and 2. by the same argument (argument-focused) |~∩AExt. Both of which further lead to floating conclusion.
Definition 5.2. Where ![]() is a knowledge base,
is a knowledge base, ![]() a sentence, and
a sentence, and ![]() is an argumentation semantics, we define the consequence relations in Table 3.
is an argumentation semantics, we define the consequence relations in Table 3.

Table 3Long description
The table consists of two columns. It read as follows: Row 1: Skeptical 1: K turnstile superscript S subscript intersection P-extensions A iff A element of intersection P-extensions subscript S (K), A is a member of every extension in P-extensions subscript S (K). Row 2: Skeptical 2: K turnstile superscript S subscript intersection A extensions A iff there is an a element A-extensions subscript S (K) s. t. Con (a) equals A, There is an argument a with Con (a) equals A that is contained in every A-extension of K. Row 3: Credulous: K turnstile superscript S subscript union extensions A iff A element of union P extensions subscript S (K), A is a member of some extension in P-extensions subscript S (K).
To avoid clutter in notation, we will omit the super- and subscripts whenever the context disambiguates or the strategy is not essential to a given claim. Note that the definition of the three consequence relations imposes a hierarchy in terms of strength, namely:

Example 16 (Example 15 cont.). Based on our extensions, we have the following consequences:

Table 016Long description
The table consists of five columns: p, q, not r, r, and s. It reads as follows: Row 1: Turnstile intersection P extensions: tick in p, tick in q, blank in not r and r, tick in s. Row 2: Turnstile intersection A extensions: tick in p and q; blank in not r, r, and s. Row 3: Turnstile union extensions: tick in all columns - p, q, not r, r, and s.
The example illustrates that a floating conclusion such as ![]() follows by
follows by ![]() but not by the more cautious
but not by the more cautious ![]() .
.
5.2 Methods based on Consistent Accumulation
Given a knowledge base ![]() , the basic idea behind the accumulation methods is to iteratively build coherent sets of defeasible elements from
, the basic idea behind the accumulation methods is to iteratively build coherent sets of defeasible elements from ![]() .Footnote 28 We will call such sets D-extensions (extensions consisting of defeasible elements). Below we identify two central methods of building D-extensions: the greedy and the temperate method. Once D-extensions have been generated by one of these methods, we can associate each D-extension
.Footnote 28 We will call such sets D-extensions (extensions consisting of defeasible elements). Below we identify two central methods of building D-extensions: the greedy and the temperate method. Once D-extensions have been generated by one of these methods, we can associate each D-extension ![]() with an A-extension
with an A-extension ![]() consisting of all the arguments based on elements in
consisting of all the arguments based on elements in ![]() . Moreover, each A-extension
. Moreover, each A-extension ![]() has the corresponding P-extension
has the corresponding P-extension ![]() as discussed in Section 5.1. Once A- and P-extensions are obtained, we define consequence relations just like in Definition 5.2 (see the overview in Fig. 9). We now discuss the two types of accumulation methods.
as discussed in Section 5.1. Once A- and P-extensions are obtained, we define consequence relations just like in Definition 5.2 (see the overview in Fig. 9). We now discuss the two types of accumulation methods.

Figure 9 Types of nonmonotonic consequence based on syntactic approaches.
Figure 9Long description
Both a. and b. leads to extensions which further leads to 1. Skeptical consequence and 2. Credulous consequence. Skeptical consequence leads to |~ ∩PExt and |~ ∩AExt. Credulous consequence leads to |~ UExt.
5.2.1 The Greedy Method
Given a knowledge base ![]() , methods based on consistent accumulation build iteratively sets of defeasible elements from
, methods based on consistent accumulation build iteratively sets of defeasible elements from ![]() . One may think of a rational agent that extends her commitment store
. One may think of a rational agent that extends her commitment store ![]() consisting of elements in
consisting of elements in ![]() in a stepwise manner. She starts off with the empty set and in each step she adds an element of
in a stepwise manner. She starts off with the empty set and in each step she adds an element of ![]() to
to ![]() or she stops the procedure. She stops when adding any new element
or she stops the procedure. She stops when adding any new element ![]() would lead to inconsistency, that is, in case she would be able to construct conflicting arguments on the basis of
would lead to inconsistency, that is, in case she would be able to construct conflicting arguments on the basis of ![]() .
.
According to the greedy method, she will only consider adding elements in ![]() to her commitment store that (a) give rise to new arguments (that is the greedy part) and (b) do not give rise to conflicting arguments. We will make this formally precise with the algorithm GreedyAcc in what follows, but we first need to introduce some concepts. Where
to her commitment store that (a) give rise to new arguments (that is the greedy part) and (b) do not give rise to conflicting arguments. We will make this formally precise with the algorithm GreedyAcc in what follows, but we first need to introduce some concepts. Where ![]() , we say that a default
, we say that a default ![]()
is triggered by
 , if
, if  ,Footnote 29
,Footnote 29is consistent with
 , if
, if  .
.
If ![]() is triggered by
is triggered by ![]() , adding
, adding ![]() to
to ![]() gives rise to new arguments in
gives rise to new arguments in ![]() . The reason for this is that for each
. The reason for this is that for each ![]() (with
(with ![]() ) there is an argument
) there is an argument ![]() with conclusion
with conclusion ![]() , and
, and ![]() . We treat defeasible assumptions
. We treat defeasible assumptions ![]() like defaults with empty left-hand sides: they are always triggered, and consistent with
like defaults with empty left-hand sides: they are always triggered, and consistent with ![]() only if
only if ![]() .
.
The algorithm GreedyAcc implements the greedy accumulation method. We note that the element ![]() in lines 3 and 4 is chosen nondeterministically.
in lines 3 and 4 is chosen nondeterministically.

Algorithm 1Long description
The Algorithm displays seven lines: 1. procedure Greedy Accumulation (K); K equals A subscript s, A subscript d, R subscript s, R subscript d. 2. Defeasible asterisk left arrow empty set; init scenario. 3. while exists d element of Defeasible (K) backslash Defeasible asterisk triggered by and consistent with Defeasible asterisk do. 4. Defeasible asterisk left arrow Defeasible asterisk union {d}; update scenario. 5. end while; no more triggered and consistent defaults. 6. return Defeasible asterisk; return D-extension. 7. end procedure.
GreedyAcc takes as input a knowledge base ![]() and outputs a D-extension
and outputs a D-extension ![]() . Its associated A-extension is given by
. Its associated A-extension is given by ![]() and its associated P-extension by
and its associated P-extension by ![]() . The latter can be used to determine our three consequence relations from Definition 5.2. We write
. The latter can be used to determine our three consequence relations from Definition 5.2. We write ![]() [resp.
[resp. ![]() ,
, ![]() ] for the set of D-[resp. A-, P-]extensions of
] for the set of D-[resp. A-, P-]extensions of ![]() (
(![]() for greedy accumulation). We are now in a position to define three consequence relations analogous to Definition 5.2 (see Table 3), for example, by:
for greedy accumulation). We are now in a position to define three consequence relations analogous to Definition 5.2 (see Table 3), for example, by:

Example 17 (Example 12 cont.). We apply GreedyAcc to the given knowledge base ![]() . There are three different runs (due to the nondeterministic nature of the algorithm):
. There are three different runs (due to the nondeterministic nature of the algorithm):

Table 01Long description
The table consists of three columns titled: Run 1, Run 2, and Run 3. Row 1: Round 1: p implies r; p implies q; p implies q. Row 2: Round 2: p implies q; p implies r; q implies not r. Row 3: P-extension: set of p, r, q, and s; set of p, r, q, and s; set of p, not r, q, and s. Row 4: A-extension: set of a subscript 1, a subscript 2, a subscript 4, and a subscript 6; set of a subscript 1, a subscript 2, a subscript 4, and a subscript 6; set of a subscript 1, a subscript 2, a subscript 3; set of a subscript 5.
Next we list consequences according to the three different consequence relations:

Table 02Long description
The table consists of five columns: p, q, not r, r, and s. It reads as follows: Row 1: Turnstile intersection P-extension, tick in columns p, q, and s. Row 2: Turnstile intersection A-extension, tick in columns p and q. Row 3: Turnstile union extension, tick in columns p, q, not r, r, and s.
Note that for ![]() we have to consider the intersection of all P-extensions
we have to consider the intersection of all P-extensions ![]() and so we get the floating conclusion
and so we get the floating conclusion ![]() (just like in Example 16). For
(just like in Example 16). For ![]() we consider the intersection of the A-extensions
we consider the intersection of the A-extensions ![]() : while
: while ![]() the floating conclusion
the floating conclusion ![]() is not in
is not in ![]() . Finally, for
. Finally, for ![]() we consider the union of all P-extensions
we consider the union of all P-extensions ![]() .
.
5.2.2 Temperate Accumulation
Our second accumulation method is nongreedy (or, temperate) in that the defeasible elements from ![]() that may be added to the commitment store
that may be added to the commitment store ![]() in each step of the algorithm can be such that they don’t give rise to new arguments. In more technical terms, our agent may also add defeasible rules which are not triggered by
in each step of the algorithm can be such that they don’t give rise to new arguments. In more technical terms, our agent may also add defeasible rules which are not triggered by ![]() . This is described in Algorithm 2, TemAcc. We use the same notation as before:
. This is described in Algorithm 2, TemAcc. We use the same notation as before: ![]() is the set of D-extensions generated by TemAcc(
is the set of D-extensions generated by TemAcc(![]() ) and
) and ![]() resp.
resp. ![]() is the corresponding set of A- resp. P-extensions. The three types of consequence relations
is the corresponding set of A- resp. P-extensions. The three types of consequence relations ![]() ,
, ![]() , and
, and ![]() are defined analogously to the greedy versions (see Table 3).
are defined analogously to the greedy versions (see Table 3).

Algorithm 2Long description
The Algorithm displays seven lines: 1. Procedure Temperate accumulation (K). 2. Defeasible asterisk left arrow empty set, init scenario. 3. while exists d element of Defeasible (K) backslash Defeasible asterisk consistent with Defeasible asterisk do. 4. Defeasible asterisk left arrow Defeasible asterisk union {d}, update scenario. 5. end while, no more consistent defaults. 6. return Defeasible asterisk, return D-extension. 7. end procedure.
Remark 1. Let us make two immediate observations to better understand how the greedy approach relates to the temperate approach. First, since defeasible assumptions are always triggered, the greedy and the temperate accumlation methods coincide for knowledge bases without defeasible rules (where ![]() ). Second, every run via GreedyAcc corresponds to the initial segment of some runs via TemAcc.
). Second, every run via GreedyAcc corresponds to the initial segment of some runs via TemAcc.
Example 18 (Example 17 cont.). We apply TemAcc to our knowledge base. There are six possible runs, omitting runs 1–3 which are analogous to Example 17:

Table 03Long description
The table consists of three columns titled: Run 4, Run 5, and Run 6. Row 1: Round 1: q implies not r; q implies not r; p implies r. Row 2: Round 2: p implies q; p implies r; q implies not r. Row 3: P-extension: set of p, not r, q, and s; set of p, r, and s; set of p, r, and s. Row 4: A-extension: set of a subscript 1, a subscript 2, a subscript 3, and a subscript 5; set of a subscript 1, a subscript 4, and a subscript 6; set of a subscript 1, a subscript 4, and a subscript 6.
In comparison with GreedyAcc we get three additional runs, namely 4–6. While run 4 is just a permutation of run 3, runs 5 and 6 give rise to new D-extensions. They show the nongreedy character of TemAcc. Consider, for instance, run 6: although in round 2 the default ![]() is both triggered and consistent with
is both triggered and consistent with ![]() , the algorithm chooses the nontriggered
, the algorithm chooses the nontriggered ![]() .
.
We list consequences according to the different notions of consequence, marking differences to GreedyAcc with [!]:

Table 04Long description
The table consists of five columns titled: p, q, not r, r, and s. Row 1: Turnstile intersection P-extension, tick in columns p and s; exclamation mark in column q; columns not r and r are empty. Row 2: Turnstile intersection A-extension, tick in column p; exclamation mark in column q; columns not r, r, and s are empty. Row 3: Turnstile union extension, tick in all five columns - p, q, not r, r, and s.
We see that ![]() does not follow anymore by
does not follow anymore by ![]() and
and ![]() .
.
While in our example every D-extension based on greedy accumulation is also one based on temperate accumulation, the example demonstrates this typically doesn’t hold vice versa. As a consequence, temperate accumulation gives rise to a more cautious style of reasoning than the greedy approach, at least in terms of the skeptical consequence relations and when there are no preferences involved (see Example 29 for a counterexample with preferences).
Figure 10 gives an overview on NMLs discussed in this Element and where they fall in terms of our classification.

Figure 10 The syntactic approach and NMLs discussed in this Element.
Figure 10Long description
Argumentation, Part Two further leads to A S P I C and logic-based. Accumulation, Part Three branches into 1. temperate, Chapter 11, which further leads to M C S-based reasoning and input/output logic and 2. greedy, Chapter 12, which further leads to default Logic.
5.2.3 Temperate Accumulation and Maxicon Sets
Alternative to the iterative procedure TemAcc, the D-extensions of temperate accumulation can also be characterized in terms of maxicon sets (for maximally consistent sets).
Definition 5.3. Given a knowledge base ![]() , a set
, a set ![]() is a maxicon set of
is a maxicon set of ![]() (in signs,
(in signs, ![]() ) iff (i)
) iff (i) ![]() is consistent in
is consistent in ![]() (i.e.,
(i.e., ![]() is consistent) and (ii) for all
is consistent) and (ii) for all ![]() , if
, if ![]() then
then ![]() is inconsistent.
is inconsistent.
Proposition 5.1. Let ![]() be a knowledge base and
be a knowledge base and ![]() .
. ![]() is a D-extension generated by TemAcc iff
is a D-extension generated by TemAcc iff ![]() .
.
Proof. Suppose ![]() . We consider a run of TemAcc in which in the
. We consider a run of TemAcc in which in the ![]() th round of the loop
th round of the loop ![]() is added to
is added to ![]() . We note that since
. We note that since ![]() is consistent in
is consistent in ![]() , so is every of its subsets. Thus, the while loop is not exited before the
, so is every of its subsets. Thus, the while loop is not exited before the ![]() th round. When the condition of the loop is checked the
th round. When the condition of the loop is checked the ![]() th time,
th time, ![]() . By the maximal consistency of
. By the maximal consistency of ![]() in
in ![]() , there is no
, there is no ![]() left for which
left for which ![]() is consistent in
is consistent in ![]() . So, TemAcc terminates and returns
. So, TemAcc terminates and returns ![]() . The other direction is similar. □
. The other direction is similar. □
Example 19 (Example 18 cont.). Our knowledge base ![]() has the maxicon sets
has the maxicon sets ![]() ,
, ![]() , and
, and ![]() . These exactly correspond to the D-extensions of temperate accumulation.
. These exactly correspond to the D-extensions of temperate accumulation.
As a consequence of Proposition 5.1 we obtain an alternative characterizations of the nonmonotonic consequence relations ![]() ,
, ![]() , and
, and ![]() .
.
Corollary 5.1. Let ![]() be a knowledge base and
be a knowledge base and ![]() a set of sentences.
a set of sentences.
1.
 iff for every
iff for every  ,
,  .
.2.
 iff there is an
iff there is an  .
.3.
 iff for some
iff for some  ,
,  .
.
The consequence relation ![]() can be equivalently characterized by means of minimal conflict sets:
can be equivalently characterized by means of minimal conflict sets:
Definition 5.4. ![]() is a minimal conflict set for
is a minimal conflict set for ![]() iff
iff ![]() is inconsistent in
is inconsistent in ![]() but every
but every ![]() is consistent in
is consistent in ![]() . The set of innocent bystanders in
. The set of innocent bystanders in ![]() ,
, ![]() , consists of all members of
, consists of all members of ![]() that are not members of minimal conflict sets for
that are not members of minimal conflict sets for ![]() .
.
Example 20 (Example 9 cont.). For our knowledge base ![]() we have
we have ![]() since every defeasible element is part of a minimal conflict. Were we to add, for instance,
since every defeasible element is part of a minimal conflict. Were we to add, for instance, ![]() to
to ![]() , resulting in
, resulting in ![]() , we would have
, we would have ![]() .
.
Proposition 5.2. Let ![]() be a knowledge base. Then, (i)
be a knowledge base. Then, (i) ![]() and (ii)
and (ii) ![]() iff
iff ![]() .
.
Proof. We show (i). (ii) follows then immediately by Corollary 5.1. Suppose ![]() . Thus, there is a minimal conflict set
. Thus, there is a minimal conflict set ![]() in
in ![]() with
with ![]() . So,
. So, ![]() is consistent and there is a
is consistent and there is a ![]() with
with ![]() and
and ![]() . So
. So ![]() . The other direction is similar and left to the reader. □
. The other direction is similar and left to the reader. □
5.3 Semantic Methods
Let us suppose a knowledge base of the form ![]() for a Tarski logic
for a Tarski logic ![]() (such as
(such as ![]() , see Section 4). A natural interpretation of
, see Section 4). A natural interpretation of ![]() is that
is that ![]() holds in the most normal situations that are consistent with the strict assumptions
holds in the most normal situations that are consistent with the strict assumptions ![]() in
in ![]() , where the standard of normality is contributed by the defeasible elements
, where the standard of normality is contributed by the defeasible elements ![]() of
of ![]() .
.
In many NMLs this idea is realized in terms of semantic selections.Footnote 30 Supposing that ![]() provides a model semantics to interpret formulas in
provides a model semantics to interpret formulas in ![]() , we consider the models of
, we consider the models of ![]() , written
, written ![]() . We write
. We write ![]() if
if ![]() is interpreted as true in
is interpreted as true in ![]() . On these models an order
. On these models an order ![]() is imposed where
is imposed where ![]() in case
in case ![]() is at least as normal as
is at least as normal as ![]() . What it means to be more normal is determined by the defeasible information in
. What it means to be more normal is determined by the defeasible information in ![]() (a concrete example is given in the next paragraph). The entailment relation is then defined by:
(a concrete example is given in the next paragraph). The entailment relation is then defined by:

that is, the most normal models of ![]() validate
validate ![]() .
.
To make this idea more concrete we return to the system of Plausible Reasoning in Section 2.3. There we modeled defeasible inferences ![]() in terms of implications
in terms of implications ![]() supplemented with normality assumptions
supplemented with normality assumptions ![]() . The strict rules
. The strict rules ![]() were contributed by classical logic. So, the knowledge base has the form
were contributed by classical logic. So, the knowledge base has the form ![]() , or in short
, or in short ![]() . We additionally assume that
. We additionally assume that ![]() is classically satisfiable (so it has a model). According to the rationale stated earlier,
is classically satisfiable (so it has a model). According to the rationale stated earlier, ![]() means that
means that ![]() holds in all situations in which the assumptions of
holds in all situations in which the assumptions of ![]() are true and which are most normal relative to the defeasible assumptions in
are true and which are most normal relative to the defeasible assumptions in ![]() .
.
Where ![]() is a classical model of
is a classical model of ![]() , let for this
, let for this ![]() be the normal part of
be the normal part of ![]() . We can then order the models by
. We can then order the models by ![]() as follows:
as follows:

In other words, the more defeasible assumptions a model verifies, the more normal it is. The most normal models will then be those in ![]() . See for an illustration Fig. 11.
. See for an illustration Fig. 11.

Figure 11 Nonmonotonic entailment by semantic selections.
Example 21 (Example 9 cont.). We take another look at ![]() from Example 9. We have, among others, the classical models of
from Example 9. We have, among others, the classical models of ![]() listed in Fig. 12 (left) whose ordering
listed in Fig. 12 (left) whose ordering ![]() is illustrated on the right. The minimal models are
is illustrated on the right. The minimal models are ![]() and
and ![]() . We therefore have, for instance,
. We therefore have, for instance, ![]() and
and ![]() .
.
Figure 12 The order ![]() on the models of Example 21. Highlighted are the
on the models of Example 21. Highlighted are the ![]() -minimal models. The atoms
-minimal models. The atoms ![]() and
and ![]() are true in every model of
are true in every model of ![]() .
.
Figure 12Long description
The row-wise data is as follows: Row 1 (highlighted): M subscript 1: 1, 1, 0, 0 and 1. Row 2 (highlighted): M subscript 2: 1, 0, 0, 1 and 0. Row 3 (highlighted): M subscript 3: 0, 1, 1, 0 and 0. Row 4: M subscript 4: 1, 0, 1,1 and 0. Row 5: M superscript i end superscript subscript 4: 0, i is an element of left curly bracket 0, 1 right curly bracket, 1, 1 and 0. Row 5: M superscript i end superscript subscript 5: 1, i is an element of left curly bracket 0, 1 right curly bracket, 0, 1 and 1. Row 6: M superscript i end superscript subscript 6: i is an element of left curly bracket 0, 1 right curly bracket, 1, 1, 0 and 1. Row 7: M superscript i end superscript subscript 7, : i is an element of left curly bracket 0, 1 right curly bracket, : j is an element of left curly bracket 0, 1 right curly bracket, 1, 1 and 1. On the left, it shows the following sequence: M superscript i, j end superscript subscript 7 leads to M superscript i end superscript subscript 6, M superscript i end superscript subscript 5, M superscript i end superscript subscript 4 and M subscript 4. M superscript i end superscript subscript 6 and M superscript i end superscript subscript 5 leads to M subscript 1. M superscript i end superscript subscript 6 leads to M subscript 3. M superscript i end superscript subscript 5 also leads to M subscript 2. M superscript i end superscript subscript 4 leads to both M subscript 3 and M subscript 2. M subscript 4 leads to M subscript 3 and M subscript 2.
Semantic selections have also been used as a model of the closed-world assumption in McCarthy’s circumscription (McCarthy, Reference McCarthy1980).Footnote 31 In our presentation this is realized by letting ![]() be a set of negated atoms.
be a set of negated atoms.
Example 22. Suppose Anne checks the online menu of the university canteen and finds the information that fries are served and that either pizza or burger is available. Consider the knowledge base ![]() where
where ![]() ,
, ![]() consists of
consists of ![]() , and
, and ![]() . In Fig. 13 we find the
. In Fig. 13 we find the ![]() -ordering of the models of
-ordering of the models of ![]() . With
. With ![]() Anne concludes, for instance,
Anne concludes, for instance, ![]() and
and ![]() . This is in accordance with the closed-world assumption: what is not listed in the menu is assumed not to be offered.
. This is in accordance with the closed-world assumption: what is not listed in the menu is assumed not to be offered.

Figure 13 Models of ![]() in Example 22 with highlighted
in Example 22 with highlighted ![]() -minimal models.
-minimal models.
Figure 13Long description
The row-wise data is as follows: Row 1 (highlighted): M subscript 1: 1, 1, 0 and 0. Row 2 (highlighted): M subscript 2: 1, 0, 1 and 0. Row 3: M subscript 3: 1, 1, 1 and 0. Row 4: M subscript 4: 1, 1, 0 and 1. Row 5: M subscript 5: 1, 0, 1 and 1. 6. M subscript 6: 1, 1, 1 and 1. The sequence shows the following: M subscript 6 leads to M subscript 4, M subscript 3 and M subscript 5. M subscript 4 and M subscript 3 further leads to M subscript 1. M subscript 3 and M subscript 5 further leads to M subscript 2.
6 A Roadmap
In this introduction we have explained the main ideas and concepts behind several core methods of NML. In what follows we will deepen our understanding of
the argumentation method in which a reasoner analyzes the interplay between arguments and their counterarguments to determine coherent sets of arguments (Part II);
the methods based on consistent accumulation, temperate and greedy, in which a reasoner gradually commits to more and more defeasible information from the given knowledge base (Part III); and
the semantic method in which a reasoner determines the most normal interpretations of the given knowledge base (Part IV).
We will study metatheoretic properties that come with these methods and discuss central logics from the literature that implement them.
Given that the field of NML comes with such a variety of systems and methods, it will also be our task to provide links between the methods. As we will see, several classes of logics belonging to different methods give rise to the same class of nonmonotonic consequence relations (see Fig. 14 for an overview).

Figure 14 Links between the various methods studied in this Element.
Figure 14Long description
The links are as follows: Semantic Methods is connected to the following: 1. Greedy Accumulation via Thm.16.1; 2. Argumentation via Thm.16.2; 3. Temperate Accumulation via Cor.15.1; Thm.15.2; 4. Fixpoints via Def.16.4. Greedy Accumulation is connected to the following: 1. Argumentation via Prop.12.1; 2. Temperate Accumulation via Rem.1; 3. Fixpoints via Prop.12.1; Thm.10.1. Argumentation leads to the follows: 1. Temperate Accumulation via Thm.11.3; Thm.9.1 and 2. Fixpoints via Def.7.1. Temperate Accumulation is connected to Fixpoints via Thm.10.1.
Part II Formal Argumentation
Argumentation theory as a study of defeasible reasoning has been proposed already by Toulmin (Reference Toulmin1958). His book provides a critique of formal logic as a model of the defeasible nature of commonsense reasoning. While in the early 1980s many NMLs were proposed, we have to wait for the most influential pioneering works in formal argumentation such as Pollock (Reference Pollock1991, Reference Pollock1995) and Dung (Reference Dung1995) until the 1990s. What distinguishes these approaches from earlier NMLs is the prominent status of arguments and defeat. The ambition is to provide both an intuitive and unifying account of defeasible reasoning. Recently, Mercier and Sperber (Reference Mercier and Sperber2017) have made a strong case for the argumentative nature of human reasoning. Together with the rich tradition in informal argumentation theory (e.g., Eemeren & Grootendorst, Reference Eemeren and Grootendorst2004; Walton et al., Reference Walton, Reed and Macagno2008) this strongly motivates formal argumentation as an account of defeasible reasoning which is close to human reasoning practices.
In this part we deepen our understanding of formal argumentation theory. In Section 7 we explain how Dung’s abstract perspective provides a way to select arguments from an argumentation framework. In Section 8, 9, we present two ways of equipping arguments with logical structure.
7 Abstract Argumentation
In formal argumentation the question as to what follows from a given defeasible knowledge base ![]() is answered by means of an argumentative analysis. It is the essential idea behind abstract argumentation (introduced by Dung (Reference Dung1995) that as soon as the arguments induced by
is answered by means of an argumentative analysis. It is the essential idea behind abstract argumentation (introduced by Dung (Reference Dung1995) that as soon as the arguments induced by ![]() are generated and collected in the set
are generated and collected in the set ![]() , and as soon as the attacks between them are determined and collected in the relation
, and as soon as the attacks between them are determined and collected in the relation ![]() , we can abstract from the concrete content of those arguments, focus on the directed graph given by
, we can abstract from the concrete content of those arguments, focus on the directed graph given by ![]() and select arguments simply by means of analyzing this graph.Footnote 32 The latter is called the argumentation framework for
and select arguments simply by means of analyzing this graph.Footnote 32 The latter is called the argumentation framework for ![]() . The argumentation semantics defined in the following definition offer criteria to select arguments that form a defendable and consistent stance. We call the selected sets of arguments A-extensions of
. The argumentation semantics defined in the following definition offer criteria to select arguments that form a defendable and consistent stance. We call the selected sets of arguments A-extensions of ![]() . A-extensions form the basis of three types of nonmonotonic consequence relations:
. A-extensions form the basis of three types of nonmonotonic consequence relations: ![]() , and
, and ![]() (see Table 3). Due to its strict division of labor between argument and attack generation, on the one hand, and argument selection with its induced notion of nonmonotonic consequence, on the other hand, formal argumentation offers a transparent and clean methodology.
(see Table 3). Due to its strict division of labor between argument and attack generation, on the one hand, and argument selection with its induced notion of nonmonotonic consequence, on the other hand, formal argumentation offers a transparent and clean methodology.
Definition 7.1 (Argumentation Semantics, Dung (1995)). Let ![]() be an argumentation framework and
be an argumentation framework and ![]() a set of arguments. We say that
a set of arguments. We say that ![]() defends
defends ![]() if for all
if for all ![]() , if
, if ![]() then there is a
then there is a ![]() such that
such that ![]() . We write
. We write ![]() for the set of arguments that are defended by
for the set of arguments that are defended by ![]() . In Table 4 we list several types of A-extensions.
. In Table 4 we list several types of A-extensions.

Table 4Long description
The table consists of two columns: X is, and iff. It reads as follows: Row 1: conflict-free; for all a, b elements of X, (a, b) not an element of att. Row 2: admissible; X subset or equal to defended (X). Row 3: complete; X equals defended (X). Row 4: grounded; X is the unique subset or equal to-minimal complete set. Row 5: preferred; X is a subset of or equal to the maximal admissible. Row 6: stable; X is conflict-free and for all a element of Arguments backslash X, there is a b element of X such that (b, a) element of Arguments.
In Fig. 15 we see the logical connections between the different argumentation semantics, all of which have been shown in Dung (Reference Dung1995). Dung also showed that, except for stable extensions, extensions of all other types always exist (they may be empty, though) and the grounded extension consists exactly of those arguments that are contained in every complete extension. Stable extensions often do not exist in frameworks that give rise to odd cycles: consider, for instance, ![]() in which neither
in which neither ![]() nor
nor ![]() is stable. In Fig. 16 we find an argumentation framework with five arguments. Depicted are some of its extensions.
is stable. In Fig. 16 we find an argumentation framework with five arguments. Depicted are some of its extensions.

Figure 15 Relations between argumentation semantics. Every extension of the type left of an arrow is also an extension of the type to its right.

Figure 16 Left: An argumentation framework composed of five arguments. Highlighted in the center and on the right are its two preferred extensions. The extension in the center is the only stable extension. The grounded extension in this example is ![]() .
.
8 ASPIC+
We now move from abstract to structured argumentation.Footnote 33 This means that our arguments will now get a logical form and attacks will be defined in terms of logical relations between arguments. ASPIC+ is one of the most prominent and most expressive frameworks in formal argumentation (Modgil & Prakken, Reference Modgil and Prakken2013). Arguments are generated on the basis of the inference rules and assumptions in a given knowledge base ![]() of the form
of the form ![]() (see Definition 5.1). We let
(see Definition 5.1). We let ![]() denote the set of all arguments induced by
denote the set of all arguments induced by ![]() . In the context of ASPIC+ we frequently find three types of attacks. In order to define them, we need to enhance knowledge bases with two elements. (a) A contrariness relation
. In the context of ASPIC+ we frequently find three types of attacks. In order to define them, we need to enhance knowledge bases with two elements. (a) A contrariness relation ![]() associates formulas with a set of contraries, for example,
associates formulas with a set of contraries, for example, ![]() or
or ![]() . (b) A naming function
. (b) A naming function ![]() allows us to refer to defeasible rules
allows us to refer to defeasible rules ![]() in the object language by
in the object language by ![]() . So our knowledge bases will have the extended form
. So our knowledge bases will have the extended form ![]() .
.
Definition 8.1. Where ![]() , we define three types of attacks:
, we define three types of attacks:
- Rebut:
 rebuts
rebuts  in
in  iff
iff  is of the form
is of the form  and
and  .
.- Undercut:
 undercuts
undercuts  in
in  iff
iff  is of the form
is of the form  where the top rule is
where the top rule is  and
and  .
.- Undermining:
 undermines
undermines  in a defeasible assumption
in a defeasible assumption  in case
in case  and
and  .
.
An informal example of a rebut is one where Peter calls upon weather report 1 to argue that it will rain, while Anne counters by calling upon weather report 2 that predicts the opposite. An undercut may occur in a case of specificity: while Peter argues that Tweety can fly based on the fact that Tweety is a bird and birds usually fly, Anne counters that the default “Birds fly” is not applicable to Tweety since Tweety is a penguin and, as such, Tweety is exceptional to “Birds fly.” Undermining happens if Anne argues against one of Peter’s basic (defeasible) assumptions: Peter may argue that they should go and buy groceries, since the shop is open, when Anne reminds him of the fact that it is a public holiday and therefore shops are closed.
Whenever the defeasible elements of a knowledge base differ in strength, not every attack may be successful. In the context of ASPIC+ we refer to successful attacks as defeats. There are various ways defeats can be defined, but they are all based on a lifting of ![]() to the level of arguments (recall that
to the level of arguments (recall that ![]() orders the defeasible elements of our knowledge base
orders the defeasible elements of our knowledge base ![]() ). We present here the most common approach, called weakest link. To simplify things, we also suppose that
). We present here the most common approach, called weakest link. To simplify things, we also suppose that ![]() is a total preorder (so it is reflexive, transitive and total). Where
is a total preorder (so it is reflexive, transitive and total). Where ![]() , we let
, we let ![]() if there is a
if there is a ![]() such that for all
such that for all ![]() ,
, ![]() . Then, for two arguments
. Then, for two arguments ![]() , we let
, we let ![]() iff
iff ![]() .Footnote 34 We now say that
.Footnote 34 We now say that ![]() defeats
defeats ![]() iff
iff ![]() attacks
attacks ![]() (Definition 8.1) and (i)
(Definition 8.1) and (i) ![]() or (ii) the attack is an undercut.Footnote 35
or (ii) the attack is an undercut.Footnote 35
In the special case in which no preference order ![]() is specified in the knowledge base,
is specified in the knowledge base, ![]() defeats
defeats ![]() iff
iff ![]() attacks
attacks ![]() . If the naming function is left unspecified in
. If the naming function is left unspecified in ![]() , undercuts are omitted.
, undercuts are omitted.
Definition 8.2. Let ![]() be a knowledge base.
be a knowledge base. ![]() is an ASPIC+-based argumentation framework, where for
is an ASPIC+-based argumentation framework, where for ![]() ,
, ![]() iff
iff ![]() defeats
defeats ![]() .
.
A-extensions obtained via the different argumentation semantics ![]() (grounded, preferred, stable, etc.) in Definition 7.1 can serve as a basis for the three types of consequences, defined exactly as in Definition 5.2 and Table 3 in Section 5.1.
(grounded, preferred, stable, etc.) in Definition 7.1 can serve as a basis for the three types of consequences, defined exactly as in Definition 5.2 and Table 3 in Section 5.1.
Example 23. We consider the knowledge base ![]() , where
, where ![]() ,
, ![]() ,
, ![]() ,
,

![]() , and
, and ![]() . In order to define
. In order to define ![]() we “rank” the members of
we “rank” the members of ![]() as indicated in the superscripts of the defaults and let the rank of the defeasible assumption
as indicated in the superscripts of the defaults and let the rank of the defeasible assumption ![]() be
be ![]() . Where
. Where ![]() , we then let
, we then let ![]() iff
iff ![]() .
.
The arguments induced by ![]() and the corresponding argumentation framework are depicted in Fig. 17. We note that
and the corresponding argumentation framework are depicted in Fig. 17. We note that ![]() is defeated by
is defeated by ![]() despite the fact that
despite the fact that ![]() is weaker than
is weaker than ![]() (by comparing their weakest links) since the attack is an undercut, for which the strength of the attacker plays no role. The defeat between
(by comparing their weakest links) since the attack is an undercut, for which the strength of the attacker plays no role. The defeat between ![]() and
and ![]() is symmetric. We have an undermine attack from
is symmetric. We have an undermine attack from ![]() to
to ![]() , while the other way around it is a rebuttal. In Table 5 we list the different argumentation extensions and the corresponding consequence relations.
, while the other way around it is a rebuttal. In Table 5 we list the different argumentation extensions and the corresponding consequence relations.

Figure 17 The argumentation framework for Example 23. Solid arrows represent rebuttals, dashed arrows undermining, and dotted arrows undercuts.

Table 5Long description
The table has four columns: Complete, Grounded, Preferred, and Stable. It reads as follows: Row 1: X subscript zero equals set of a subscript zero, b subscript one; X subscript zero; blank; blank. Row 2: X subscript one equals set of a subscript zero, b subscript one, b subscript two, b subscript three; blank; X subscript one; blank. Row 3: X subscript two equals set of a subscript zero, b subscript one, c subscript zero, c subscript one, c subscript two, c subscript three; blank; X subscript two; X subscript two. Row 4: Turnstile intersection P-extension: set of p and s; set of p and s; set of p, s, and u; set of p, q, u, s, t, and v. Row 5: Turnstile intersection A-extension: set of p and s; set of p and s; set of p and s; set of p, q, u, s, t, and v. Row 6: Turnstile union extension: S equals set of p, q, not q, t, s, not s, u, and v; set of p and s; S; set of p, q, u, s, t, and v.
Example 24. Consider the knowledge base ![]() (without preferences), where
(without preferences), where ![]() and
and ![]() . We have, for instance, the following arguments:
. We have, for instance, the following arguments:

Table 05Long description
The six knowledge base rules are: 1. a subscript 1 equals p implies q; 2. a subscript 2 equals p implies s; 3. a subscript 3 equals p implies not (q and s); 4. a subscript 4 equals a subscript 1, a subscript 2 right arrow q and s; 5. a subscript 5 equals a subscript 1, a subscript 3 right arrow not s; and 6. a subscript 6 equals a subscript 2, a subscript 3 right arrow not q.
The reader may be puzzled by on odd restriction in Definition 8.1, namely, when attacking an argument in which inference rules have been applied, only attacks in the heads of defeasible rules are allowed. Why did we not simply define: ![]() attacks
attacks ![]() iff
iff ![]() ? Figure 18 features the resulting argumentation framework. We observe that there is now a preferred (and stable) extension with the conclusions
? Figure 18 features the resulting argumentation framework. We observe that there is now a preferred (and stable) extension with the conclusions ![]() and
and ![]() . This may be considered as unwanted if we want our A-extensions to represent rational and therefore consistent stances of debaters.
. This may be considered as unwanted if we want our A-extensions to represent rational and therefore consistent stances of debaters.

Figure 18 Example 24 with the inconsistent preferred and stable extension ![]() .
.
Problems such as the one highlighted in our previous example show the need for a set of design desiderata, or rationality postulates, that argumentation-based NMLs should fulfill. The following have become standard in the literature (Caminada & Amgoud, Reference Caminada and Amgoud2007). Given a standard of consistency, a knowledge base ![]() , an argumentation semantics, an A-extension
, an argumentation semantics, an A-extension ![]() based on it, and the argumentation framework
based on it, and the argumentation framework ![]() , we define
, we define
- Direct consistency.
For all
 ,
,  is consistent.
is consistent.- Indirect consistency.
 is consistent.
is consistent.- Strict closure.
Where
 and
and  , also
, also  .
.
In Example 24 we have seen that allowing in our simple framework for “unrestricted” rebut results in a violation of indirect consistency and strict closure,Footnote 36 unlike the unrestricted rebut of Definition 8.1.
Another rationality property has to do with syntactic relevance. We give an example to motivate it.
Example 25. Consider the knowledge base ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() . Clearly, the grounded extension will contain the argument
. Clearly, the grounded extension will contain the argument ![]() and therefore both
and therefore both ![]() and
and ![]() follow with
follow with ![]() and
and ![]() .
.
We now extend our knowledge base to ![]() , where
, where ![]() and
and ![]() . Figure 19 shows a relevant excerpt of the argumentation framework for
. Figure 19 shows a relevant excerpt of the argumentation framework for ![]() . Argument
. Argument ![]() is obtained by the rule
is obtained by the rule ![]() that holds due to the classical explosion principle.
that holds due to the classical explosion principle.
Note that we only added information to ![]() that is syntactically irrelevant to both
that is syntactically irrelevant to both ![]() and
and ![]() . Nevertheless, the grounded extension of
. Nevertheless, the grounded extension of ![]() only consists of arguments that do not involve defeasible rules (such as
only consists of arguments that do not involve defeasible rules (such as ![]() or
or ![]() ). Therefore,
). Therefore, ![]() is not part of it. As a consequence,
is not part of it. As a consequence, ![]() and
and ![]() will deliver only classical consequences of
will deliver only classical consequences of ![]() , but not anymore
, but not anymore ![]() .
.

Figure 19 Excerpt of the argumentation framework of Example 25.
The rationality property noninterference (Caminada et al., Reference Caminada, Carnielli and Dunne2012) expresses, informally, that adding syntactically irrelevant information to a knowledge base should not lead to the loss of consequences. Our example shows that this property does not hold for grounded extensions.
9 Logic-Based Argumentation
Another line of research within structured argumentation is logic-based (or deductive) argumentation. In what follows we will show that it has close connections to temperate accumulation and that, just as in the case of ASPIC+, ill-conceived combinations of attack forms and argumentation semantics can lead to undesired metatheoretic behavior.
Logic-based argumentation has been proposed, for instance, in Arieli and Straßer (Reference Arieli and Straßer2015) and Besnard and Hunter (Reference Besnard and Hunter2001). Our presentation follows the approach in Arieli et al. (Reference Arieli, Borg and Straßer2023), but simplifies it in some respects.Footnote 37 Knowledge bases have the form ![]() , where the set of strict rules
, where the set of strict rules ![]() is induced by an underlying Tarski logic
is induced by an underlying Tarski logic ![]() .
.
In Definition 5.1, arguments are proof trees. In the context of knowledge bases without defeasible rules and for which the strict rules are induced by a base logic ![]() , arguments are often modeled more abstractly simply as premise-conclusion pairs.
, arguments are often modeled more abstractly simply as premise-conclusion pairs.
Definition 9.1. Where ![]() , we let
, we let ![]() . Where
. Where ![]() is an argument in
is an argument in ![]() ,
, ![]() and
and ![]() . Where
. Where ![]() ,
, ![]() .
.
Attacks between arguments can be defined in various ways. Some examples are given in Table 6.Footnote 38

Table 6Long description
The table consists of four columns: Type, Attacker, Attacked, and Conditions. Row 1: Defeat; A subscript 1, not A subscript 2; A subscript 2 union A prime subscript 2, C; A subscript 2 not equal to the empty set, A subscript 2 is a subset of A subscript d. Row 2: DirDefeat; A subscript 1, not A; A subscript 2 union the set containing A, C; A is an element of A subscript d. Row 3: ConDefeat; A subscript 1, not A subscript 2 back slash A subscript s; A subscript two, C; A subscript 1 is a subset of A subscript s, A subscript 2 intersection A subscript d is not equal to the empty set.
Definition 9.2. Let ![]() be a nonempty set of attack types based on the knowledge base
be a nonempty set of attack types based on the knowledge base ![]() from Table 6, arguments be defined as in Definition 9.1, and
from Table 6, arguments be defined as in Definition 9.1, and ![]() be defined by
be defined by ![]() iff
iff ![]() attacks
attacks ![]() in view of an attack type in
in view of an attack type in ![]() . We let
. We let ![]() be the argumentation framework induced by
be the argumentation framework induced by ![]() and
and ![]() . For a given argumentation semantics
. For a given argumentation semantics ![]() (see Table 4) and an attack type
(see Table 4) and an attack type ![]() , we denote the corresponding set of A-extensions by
, we denote the corresponding set of A-extensions by ![]() and the underlying nonmonotonic consequences analogous to Table 3. For instance,
and the underlying nonmonotonic consequences analogous to Table 3. For instance,
 iff in every
iff in every  -extension
-extension  there is an argument
there is an argument  .
.
Let in the following ![]() , and
, and ![]() .
.
Example 26. We let ![]() , where
, where ![]() and
and ![]() . In Fig. 20 we see (a fragment of) the argumentation framework
. In Fig. 20 we see (a fragment of) the argumentation framework ![]() . We note that for
. We note that for ![]() the grounded extension concludes
the grounded extension concludes ![]() , but not for
, but not for ![]() . The latter is counterintuitive since
. The latter is counterintuitive since ![]() is syntactically unrelated to the conflicts in
is syntactically unrelated to the conflicts in ![]() and
and ![]() and the conflict in
and the conflict in ![]() and
and ![]() . On the right (center and bottom) we see the two stable resp. preferred extensions for this example. In both cases we can conclude
. On the right (center and bottom) we see the two stable resp. preferred extensions for this example. In both cases we can conclude ![]() and the floating conclusion
and the floating conclusion ![]() .
.
We also note a correspondence between the argumentative extensions and selections based on maxicon sets of ![]() (see Section 5.2.3). We have
(see Section 5.2.3). We have ![]() and
and ![]() . So, in our example, the grounded semantics induces the same consequence relations
. So, in our example, the grounded semantics induces the same consequence relations ![]() and
and ![]() as
as ![]() for
for ![]() , while the stable and preferred semantics (
, while the stable and preferred semantics (![]() ) induce the same consequence relations
) induce the same consequence relations ![]() as
as ![]() for any
for any ![]() (recall Section 5.2.3 and Corollary 5.1). This is not coincidental, as we see with Theorem 9.1.
(recall Section 5.2.3 and Corollary 5.1). This is not coincidental, as we see with Theorem 9.1.

Figure 20 Example 26. Left: We let ![]() . The black nodes represent the grounded extension. Dashed arrows correspond to those Defeats and ConDefeats that are not DirDefeats, while solid arrows are (also) DirDefeats. Right top: The grounded extension for
. The black nodes represent the grounded extension. Dashed arrows correspond to those Defeats and ConDefeats that are not DirDefeats, while solid arrows are (also) DirDefeats. Right top: The grounded extension for ![]() . Right center and bottom: the two stable resp. preferred extensions.
. Right center and bottom: the two stable resp. preferred extensions.
In fact, there is a close relation between logic-based argumentation and reasoning based on temperate accumulation.Footnote 39
Theorem 9.1 (Arieli et al., 2021b). Let ![]() be a knowledge base. We have:
be a knowledge base. We have:
1.
 and
and  , for
, for  and
and  .
.2.
 and
and  , for
, for  and
and  .
.
While Theorem 9.1 identifies well-behaved combinations of attack types and argumentation semantics, the following two examples show that one has to be careful in order to avoid counter-intuitive behavior. (Recall similar problems in the context of ASPIC+ in Section 8.)
Example 27. We consider the knowledge base

In Fig. 21 we see that with ![]() we obtain a problematic stable and preferred extension
we obtain a problematic stable and preferred extension ![]() featuring the inconsistent set of conclusions
featuring the inconsistent set of conclusions ![]() violating the indirect consistency property (see Section 8). On the right we find the argumentation framework with
violating the indirect consistency property (see Section 8). On the right we find the argumentation framework with ![]() where
where ![]() is not anymore preferred (and therefore also not stable).
is not anymore preferred (and therefore also not stable).

Figure 21 Example 27. Left: ![]() . Right:
. Right: ![]() .
.
Selected Further Readings
An excellent overview on the state of the art in formal argumentation is provided by the handbook series Handbook of Formal Argumentation (Baroni et al. Reference Baroni, Gabbay and Giacomin2018) and Handbook of Formal Argumentation (Gabbay et al. Reference Gabbay, Giacomin, Guillermo and Thimm2021). Volume 5 of Argument & Computation contains several tutorials on central approaches, such as Modgil and Prakken (Reference Modgil and Prakken2014), and Toni (Reference Toni2014).
Already in the seminal Dung (Reference Dung1995) several embeddings of NMLs in abstract argumentation were provided, including default logic. A recent overview on structured argumentation can be found in Arieli et al., (Reference Arieli, Borg, Heyninck and Straßer2021a). Links to default logic with a special emphasis on preferences are established in, for example, Liao et al. (Reference Liao, Oren, van der Torre and Villata2018); Straßer and Pardo (Reference Straßer, Pardo, Liu, Marra, Portner and Van de Putte2021), and Young et al. (Reference Young, Modgil and Rodrigues2016), connections to maxicon sets are numerous (Arieli et al., Reference Arieli, Borg and Heyninck2019; Cayrol, Reference Cayrol1995; Heyninck & Straßer, Reference Heyninck and Straßer2021b; Reference Vesic2013), and links to adaptive logics are to be found in Borg (Reference Borg2020), Heyninck and Straßer (Reference Heyninck, Straßer, Kern-Isberner and Wassermann2016), and Straßer and Seselja (Reference Straßer and Seselja2010), and to logic programming in Caminada and Schulz (Reference Caminada and Schulz2017); Heyninck and Arieli (Reference Heyninck and Arieli2019), and Schulz and Toni (Reference Schulz and Toni2016). Nonmonotonic reasoning properties of several systems of structured argumentation are studied in Borg and Straßer (Reference Borg, Straßer and Lang2018; Reference Čyras, Toni, Black and Modgil2015; Čyras and Toni (Reference Heyninck and Straßer2021a), and Li et al. (Reference Li, Oren and Parsons2018). Probabilistic approaches can be found, for instance, in Haenni (Reference Haenni2009); Hunter and Thimm (Reference Hunter and Thimm2017), and Straßer and Michajlova (Reference Straßer and Michajlova2023). The Handbook of Formal Argumentation offers an excellent overview and detailed surveys of central topics in the area (see Handbook of Formal Argumentation, Reference Gabbay, Giacomin, Guillermo and Thimm2021).
Part III Consistently Accumulating Defeasible Information
10 Consistent Accumulation: General Setting
In this section we study in a systematic way the two variants of the consistent accumulation method: greedy and temperate accumulation. First, in Section 10.1 we present the algorithms GreedyAcc and TemAcc in the settings of knowledge bases in the general form of Section 4 (including preferences). Then, in Section 10.2 we present alternative characterizations in terms of fixed points. In Section 10.3 we study metatheoretic properties of extensions and nonmonotonic consequences. While this section provides a general perspective, we dive into particularities and concrete systems in Sections 11 and 12.
10.1 Greedy and Temperate Accumulation
We now consider knowledge bases with all components

as introduced in Section 4, with the only restriction that the set of defeasible elements in ![]() ,
, ![]() , is finite. As compared to Part I, we slightly generalize our two accumulation methods, greedy and temperate accumulation, by taking into account preferences among elements in
, is finite. As compared to Part I, we slightly generalize our two accumulation methods, greedy and temperate accumulation, by taking into account preferences among elements in ![]() . For this, we suppose there to be a reflexive and transitive order
. For this, we suppose there to be a reflexive and transitive order ![]() on
on ![]() .
.
In the following we suppose for any given ![]() a formal language
a formal language ![]() , a class of associated knowledge bases
, a class of associated knowledge bases ![]() , a notion of what it means that a set of sentences
, a notion of what it means that a set of sentences ![]() is (in)consistent, for each
is (in)consistent, for each ![]() a set
a set ![]() of arguments based on
of arguments based on ![]() , and for each
, and for each ![]() a notion
a notion ![]() of conclusion and
of conclusion and ![]() of the defeasible part of
of the defeasible part of ![]() (e.g., Definitions 5.1, 9.1 and 11.3). Moreover, where
(e.g., Definitions 5.1, 9.1 and 11.3). Moreover, where ![]() ,
, ![]() . Many of the results presented in this part of the Element (e.g., the metatheoretic insights in Section 10.3, 11.1) will not rely on a specific underlying notion of argument, but apply to many concrete logics from the literature (such as the ones presented in Section 11.3.1, 11.3.2).
. Many of the results presented in this part of the Element (e.g., the metatheoretic insights in Section 10.3, 11.1) will not rely on a specific underlying notion of argument, but apply to many concrete logics from the literature (such as the ones presented in Section 11.3.1, 11.3.2).
We first discuss greedy accumulation. As explained in Section 5.2, the main idea behind the algorithm is to build a D-extension by accumulating (1) triggered and (2) consistent defeasible information ![]() . Since we now consider prioritized defeasible information, we add the requirement (3) that
. Since we now consider prioritized defeasible information, we add the requirement (3) that ![]() is
is ![]() -maximal with properties (1) and (2). Let us make this precise.
-maximal with properties (1) and (2). Let us make this precise.
Definition 10.1. For a defeasible rule ![]() , we let
, we let ![]() and
and ![]() . Similarly, for any
. Similarly, for any ![]() , we let
, we let ![]() and
and ![]() . Then, where
. Then, where ![]() and
and ![]() , we say that
, we say that
 is triggered by
is triggered by  iff
iff  .Footnote 40
.Footnote 40 is consistent with
is consistent with  iff
iff  is consistent.
is consistent. iff
iff  and for all
and for all  ,
,  .
.
We write ![]() for all the elements in
for all the elements in ![]() that are consistent with
that are consistent with ![]() ,
, ![]() for all elements in
for all elements in ![]() triggered by
triggered by ![]() , and
, and ![]() for all the elements in
for all the elements in ![]() that are triggered by
that are triggered by ![]() .
.
Note that our definition implies that defeasible assumptions are automatically triggered. Algorithm GreedyAcc generates D-extensions for the greedy accumulation method. The A- resp. the P-extension associated with a D-extension ![]() is defined by
is defined by ![]() resp. by
resp. by ![]() . We write
. We write ![]() resp.
resp. ![]() for the set of A-resp. P-extensions for
for the set of A-resp. P-extensions for ![]() . In this way we obtain the consequence relations
. In this way we obtain the consequence relations ![]() and
and ![]() (see Table 3), where the superscript indicates that the underlying extensions have been obtained via greedy accumulation.
(see Table 3), where the superscript indicates that the underlying extensions have been obtained via greedy accumulation.
Example 28 (The order puzzle, Example 11 cont.). We recall the knowledge base ![]() containing the preference order:
containing the preference order: ![]() (supposing reflexivity and transitivity). Our algorithm GreedyAcc has exactly one run in which in the first round of the loop
(supposing reflexivity and transitivity). Our algorithm GreedyAcc has exactly one run in which in the first round of the loop ![]() is added to
is added to ![]() , since it is the
, since it is the ![]() -preferred one among the two triggered and consistent defaults
-preferred one among the two triggered and consistent defaults ![]() and
and ![]() . In the second round only
. In the second round only ![]() is triggered and consistent. So we end up with
is triggered and consistent. So we end up with ![]() and GreedyAcc terminates since the remaining default
and GreedyAcc terminates since the remaining default ![]() is inconsistent with the set of the already selected ones. This implies that
is inconsistent with the set of the already selected ones. This implies that ![]() for all
for all ![]() .
.

Algorithm 3Long description
The Algorithm displays in eight lines: 1. procedure Greedy accumulation (K), where K equals (A subscript s, A subscript d, R subscript s, R subscript d, R subscript m, subset or equal). 2. Defeasible asterisk left arrow empty set, init D-extension. 3. while Trig subscript K superscript T (Defeasible asterisk) backslash Defeasible asterisk not equals empty set do. 4. (nondeterministically) choose d element of max subscript subset or equal to (Trig subscript K superscript T (Defeasible asterisk) backslash Defeasible asterisk). Defeasible asterisk left arrow Defeasible asterisk union the set containing d, update D-extension. 6. end while, no more triggered and consistent defaults. 7. return Defeasible asterisk, return D-extension. 8. end procedure.
We now move to temperate accumulation which is characterized by the algorithm TemAcc. Recall that the main difference from greedy accumulation is that, when building D-extensions, temperate accumulation also considers nontriggered defaults that are consistent with the already accumulated defeasible elements. The set of D-, A-, and P-extension of ![]() (denoted by
(denoted by ![]() ,
, ![]() , and
, and ![]() ) and the consequence relations
) and the consequence relations ![]() , and
, and ![]() are defined in analogy to the greedy case.
are defined in analogy to the greedy case.

Algorithm 4Long description
The Algorithm displays code in eight lines: 1. procedure Temperate accumulation(K), where K equals (A subscript s, A subscript d, R subscript s, R subscript d, R subscript m, subset or equal). 2. Defeasible asterisk left arrow empty set, init D-extension. 3. while Cons subscript K superscript T (Defeasible asterisk) backslash Defeasible asterisk not equals empty set do. 4. (nondeterministically) choose d element of maximum subscript subset or equal to (Cons subscript K (Defeasible asterisk) backslash Defeasible asterisk). 5. Defeasible asterisk left arrow Defeasible asterisk union {d}, update D-extension. 6. end while, no more consistent defaults. 7. return Defeasible asterisk, return D-extension. 8. end procedure.
Example 29 (Example 28 cont.). We now apply TemAcc to ![]() . There is again only one possible run: in the first round we choose (the nontriggered)
. There is again only one possible run: in the first round we choose (the nontriggered) ![]() as it is preferred over the other two defaults. In the second round we choose
as it is preferred over the other two defaults. In the second round we choose ![]() as it is preferred over
as it is preferred over ![]() . This is when TemAcc terminates since the only remaining default
. This is when TemAcc terminates since the only remaining default ![]() is not consistent with
is not consistent with ![]() . This implies that
. This implies that ![]() for all
for all ![]() .
.
This shows that unlike in the nonprioritized setting, for knowledge bases with preferences there may be D-extensions for temperate accumulation that do not correspond to D-extensions for greedy accumulation.
10.2 Accumulation and Fixed Points
In this section we consider alternative characterizations of our two accumulation methods. Instead of using iterative algorithms such as TemAcc and GreedyAcc, we now describe these reasoning styles, that is, the D-extension they characterize, as fixed points of specific operations ![]() . The underlying idea is that the possible final products of the reasoning process of a rational agent can be characterized as equilibrium states based on the given knowledge base
. The underlying idea is that the possible final products of the reasoning process of a rational agent can be characterized as equilibrium states based on the given knowledge base ![]() . In what follows, we only consider knowledge bases without preferences.
. In what follows, we only consider knowledge bases without preferences.
Lemma 10.1. Let ![]() be a knowledge base. Then,
be a knowledge base. Then, ![]() iff
iff ![]() .
.
Proof. Let ![]() . By Definition 5.3 (i) and Definition 10.1,
. By Definition 5.3 (i) and Definition 10.1, ![]() . If
. If ![]() , then
, then ![]() by Definition 5.3 (ii), and so
by Definition 5.3 (ii), and so ![]() . The other direction is similar. □
. The other direction is similar. □
Theorem 10.1. Let ![]() be a knowledge base and
be a knowledge base and ![]() .
.
1.
 is a D-extension generated by TemAcc iff
is a D-extension generated by TemAcc iff  .
.2.
 is a D-extension generated by GreedyAcc iff
is a D-extension generated by GreedyAcc iff  .
.
Proof. Item 1 follows with Proposition 5.1 and Lemma 10.1.
Consider Item 2. (![]() ) Let
) Let ![]() be produced by GreedyAcc such that
be produced by GreedyAcc such that ![]() in round
in round ![]() and
and ![]() for
for ![]() .
.
“![]() ”. Let
”. Let ![]() . So
. So ![]() for some
for some ![]() . We have to show that
. We have to show that ![]() . Since
. Since ![]() ,
, ![]() . Assume for a contradiction that
. Assume for a contradiction that ![]() . So, there is a
. So, there is a ![]() -minimal
-minimal ![]() such that
such that ![]() is inconsistent in
is inconsistent in ![]() . Let
. Let ![]() be the element in
be the element in ![]() with maximal index. If
with maximal index. If ![]() ,
, ![]() . If
. If ![]() ,
, ![]() . Each case is a contradiction. So,
. Each case is a contradiction. So, ![]() and so
and so ![]() .
.
“![]() ”. Let
”. Let ![]() . By the guard of the while-loop (line 3),
. By the guard of the while-loop (line 3), ![]() .
.
(![]() ) Let now
) Let now ![]() . It can easily be seen that
. It can easily be seen that ![]() can be enumerated by
can be enumerated by ![]() in such a way that
in such a way that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and
and ![]() . Moreover, there is a run of GreedyAcc in which each
. Moreover, there is a run of GreedyAcc in which each ![]() is added to the scenario at round
is added to the scenario at round ![]() for each
for each ![]() . Note that the algorithm terminates after round
. Note that the algorithm terminates after round ![]() since
since ![]() . □
. □
An advantage of the characterization of D-extensions in terms of fixed points as in Theorem 10.1 or with maxicon-sets as in Proposition 5.1 is that the restriction to finite sets of defeasible information ![]() in our knowledge bases can be lifted. The restriction was necessary to warrant the termination of GreedyAcc and TemAcc.
in our knowledge bases can be lifted. The restriction was necessary to warrant the termination of GreedyAcc and TemAcc.
10.3 More on Nonmonotonic Reasoning Properties
In this section we take another, more detailed look at abstract properties of nonmonotonic consequence relations (see Section 2.2). To simplify things, we will study them in a nonprioritized setting.
10.3.1 Knowledge Bases and Abstract Properties of Consequence Relations
Now that we have a better understanding of knowledge bases, let us have another look at the properties introduced in Section 2.2. Recall that consequence relations are used to study the question of what follows from a given defeasible knowledge base. An ![]() gives an answer to this question on the basis of the coherent units of information provided by its underlying model of knowledge representation.Footnote 41 It gives rise to nonmonotonic consequence relations
gives an answer to this question on the basis of the coherent units of information provided by its underlying model of knowledge representation.Footnote 41 It gives rise to nonmonotonic consequence relations ![]() that hold between knowledge bases (in its associated class
that hold between knowledge bases (in its associated class ![]() ) and sentences in its object language
) and sentences in its object language ![]() . In proof-theoretic approaches consequences will be determined by the given extensions of the knowledge base, while in semantic approach they will be based on (typically a selection of) its models.
. In proof-theoretic approaches consequences will be determined by the given extensions of the knowledge base, while in semantic approach they will be based on (typically a selection of) its models.
In the remainder of the Element it will be our task to explain different central methods of knowledge representation and consequence underlying NMLs. Before doing so, we have to comment on what the introduction of knowledge bases means for the abstract study of nonmonotonic consequence presented in Section 2.2. There, the left-hand side of ![]() merely consisted of sets of sentences, but defeasible knowledge bases typically come with more structure. That means that the reasoning principles discussed in Section 2.2 need to be disambiguated. For example, one may distinguish between a strict and a defeasible form of cautious (or rational) monotonicity (see Fig. 22). Where
merely consisted of sets of sentences, but defeasible knowledge bases typically come with more structure. That means that the reasoning principles discussed in Section 2.2 need to be disambiguated. For example, one may distinguish between a strict and a defeasible form of cautious (or rational) monotonicity (see Fig. 22). Where
 ,
, ,
,

Figure 22 Versions of cautious monotonicity with defeasible knowledge bases
Figure 22Long description
Conclusions lead to strict A subscript s via C M subscript s. Conclusions lead to defeasible A subscript d via C M subscript d. Inference engine loops back to inference engine via meta R subscript m.
and where ![]() , we define:
, we define:

Table 06Long description
The list is as follows: 1. CM subscript i (turnstile): K turnstile A and K turnstile B implies K oplus subscript i B turnstile A. 2. CT subscript i (turnstile): K turnstile A and K oplus subscript i B turnstile A implies K turnstile B. 3. C subscript i (turnstile): CM subscript i (turnstile) and CT subscript i (turnstile) hold. 4. M subscript i (turnstile): K turnstile A implies K oplus subscript i B turnstile A. 5. OR subscript i (turnstile): K oplus subscript i A turnstile C and K oplus subscript i B turnstile C implies K oplus subscript i (A or B) turnstile C. 6. LLE subscript i (turnstile): A element of Cn subscript R subscript s of set of B, B element of Cn subscript R subscript s of set of A, and K oplus subscript i A turnstile C implies K oplus subscript i B turnstile C. 7. Ref (turnstile): K oplus subscript s A turnstile A. 8. RW (turnstile): K turnstile A and B element of Cn subscript R subscript s of set of A implies K turnstile B.
Since it seems not desirable to expect for defeasible assumptions to be derivable in just any given context, we didn’t include reflexivity under the addition of defeasible assumptions (![]() ). Similarly, we only stated the RW and LLE in the less demanding version relative to strict rules (as opposed to defeasible rules).
). Similarly, we only stated the RW and LLE in the less demanding version relative to strict rules (as opposed to defeasible rules).
Definition 10.2. Let ![]() . A nonmonotonic consequence relation
. A nonmonotonic consequence relation ![]() is
is ![]() -cumulative if it satisfies RW
-cumulative if it satisfies RW ![]() , LLE
, LLE ![]() , Ref(
, Ref(![]() ), and C
), and C ![]() . It is
. It is ![]() -preferential if it additionally satisfies OR
-preferential if it additionally satisfies OR ![]() .
.
10.3.2 Nonmonotonic Reasoning Properties and Extensions
So far, we have discussed cumulativity and related properties in the context of nonmonotonic consequence relations. We now consider these and similar properties from the perspective of extensions. The shift in perspective is well-motivated since, after all, nonmonotonic consequence is determined by the given extensions (see Table 3). In view of this, nonmonotonic reasoning properties should have counterparts from a perspective more focused on knowledge representation. E.g., where cautious monotonicity and transitivity concern the robustness of the consequence set under the addition of consequences to the knowledge base, we should expect a similar robustness of the set of extensions.
In this section we show that many metatheoretic properties hold for both accumulation methods if the underlying notion of argument satisfies some basic requirements.
Given a knowledge base ![]() , a sentence
, a sentence ![]() , and a set
, and a set ![]() , we let
, we let ![]() ,
, ![]() ,
, ![]() , and
, and

Definition 10.3. Let ![]() be an NML based on consistent accumulation with an associated class of knowledge bases
be an NML based on consistent accumulation with an associated class of knowledge bases ![]() and let
and let ![]() . We define the following properties for
. We define the following properties for ![]() . For all
. For all ![]() and all sentences
and all sentences ![]() , if
, if ![]() , then
, then
CM
 (PExt) holds, if
(PExt) holds, if  implies
implies  .
.CM
 (DExt) holds, if
(DExt) holds, if  implies
implies  .
.CT
 (PExt) holds, if
(PExt) holds, if  implies
implies  .
.CT
 (DExt) holds, if
(DExt) holds, if  implies
implies  .
.
Moreover,
C
 (PExt) holds, if CT
(PExt) holds, if CT  (PExt) and CM
(PExt) and CM  (PExt) hold.
(PExt) hold.C
 (DExt) holds, if CT
(DExt) holds, if CT  (DExt) and CM
(DExt) and CM  (DExt) hold.
(DExt) hold.
These notions are related as in Fig. 23 (see Theorem 10.2) for D-extensions induced by greedy or temperate accumulation and for any underlying notion of argument, as long as it fulfills the following requirements.

Figure 23 Relations between extensional and consequence-based notions of cumulativity, cautious transitivity and monotonicity (where ![]() ).
).
(arg-trans) Let ![]() and
and ![]() . If there is an
. If there is an ![]() with
with ![]() , then for all
, then for all ![]() , there is a
, there is a ![]() with
with ![]() .
.
The criterion states that adding a conclusion ![]() to
to ![]() and
and ![]() does not generate new conclusions:
does not generate new conclusions: ![]() .
.
(arg-mono) Let ![]() and
and ![]() . We have
. We have ![]() .
.
The criterion expresses that adding assumptions to a knowledge base does not result in the loss of arguments.
(arg) (arg-trans) and (arg-mono).
Since by the definition of ![]() , we have
, we have ![]() for any
for any ![]() , by (arg-mono),
, by (arg-mono), ![]() . Therefore, if (arg) holds and
. Therefore, if (arg) holds and ![]() , then
, then ![]() .
.
Lemma 10.2. Definitions 5.1 and 9.1 satisfy (arg).
Proof. In the case of Definition 9.1 this follows by the monotonicity and the transitivity of ![]() . (arg-mono) follows directly by Definition 5.1. For (arg-trans), let
. (arg-mono) follows directly by Definition 5.1. For (arg-trans), let ![]() , where
, where ![]() for some
for some ![]() . Let
. Let ![]() be the result of replacing every
be the result of replacing every ![]() in
in ![]() by
by ![]() . Clearly
. Clearly ![]() and
and ![]() . □
. □
CT ![]() (DExt) and CM
(DExt) and CM ![]() (DExt) (highlighted in Fig. 23) have a central place. Instead of showing the corresponding properties CT
(DExt) (highlighted in Fig. 23) have a central place. Instead of showing the corresponding properties CT ![]() and CT
and CT ![]() for the nonmonotonic consequence relations directly, one can show the corresponding extensional principles.Footnote 42
for the nonmonotonic consequence relations directly, one can show the corresponding extensional principles.Footnote 42
Theorem⋆ 10.2. Given (arg), the logical dependencies of Fig. 23 hold for both accumulation methods.
Moreover, both accumulation methods satisfy CT ![]() (DExt) if (arg) holds.
(DExt) if (arg) holds.
Proposition⋆ 10.1. Let ![]() . Given (arg), CT
. Given (arg), CT![]() (DExt) holds for both accumulation methods.
(DExt) holds for both accumulation methods.
Also LLE and RW hold given some intuitive requirements on the underlying notion of argument.
(arg-re) Let ![]() . If
. If ![]() and
and ![]() , then for every
, then for every ![]() there is a
there is a ![]() with
with ![]()

The criterion expresses that if assumptions in the knowledge base are replaced with equivalent ones, we can still conclude the same sentences.
(arg-strict) For all ![]() , (i)
, (i) ![]() and (ii) for all
and (ii) for all ![]() and all
and all ![]() , if
, if ![]() then
then ![]() .
.
The criterion expresses that every strict assumption gives rise to an argument and arguments can be extended by strict rules.
Lemma 10.3. Definitions 5.1 and 9.1 satisfy (arg-re), and (arg-strict).
Proof. Consider Definition 5.1. (arg-strict) follows trivially. For (arg-re), let ![]() and
and ![]() . So, there is a
. So, there is a ![]() of the form
of the form ![]() . Let
. Let ![]() be the result of replacing each
be the result of replacing each ![]() in
in ![]() by
by ![]() . Then
. Then ![]() and
and ![]() satisfy the requirements of (arg-re). The proof for Definition 9.1 is similar, making use of the transitivity of
satisfy the requirements of (arg-re). The proof for Definition 9.1 is similar, making use of the transitivity of ![]() . □
. □
Proposition⋆ 10.2. Let ![]() ,
, ![]() and
and ![]() . If (arg-re), LLE
. If (arg-re), LLE![]() (
(![]() ) holds.
) holds.
Proposition⋆ 10.3. Let ![]() and
and ![]() . If (arg-strict), Ref(
. If (arg-strict), Ref(![]() ) and RW(
) and RW(![]() ) hold.
) hold.
11 Temperate Accumulation: Properties and Some Concrete Systems
In this section we study temperate accumulation in more detail. We show that it gives rise to preferential consequence relations (Section 11.1), if some basic conditions are met. Moreover, by “naming” default rules the structure of knowledge bases can be simplified (Section 11.2.1). Temperate accumulation can be characterized in terms of formal argumentation (Section 11.2.2).
Finally, we present two families of systems based on temperate accumulation: reasoning with maxicon-sets (Section 11.3.1) and input–output logics (Section 11.3.2) and apply the results from Section 11.1 to them.
11.1 Cumulativity and Preferentiality
The temperate accumulation method often yields cumulative or even preferential consequence relations. Table 7 gives an overview for the following two classes of knowledge bases:
the “universal” class
 containing all knowledge bases of the form
containing all knowledge bases of the form  ;
;the class
 containing all knowledge bases of the form
containing all knowledge bases of the form  for a Tarski logic
for a Tarski logic  . In this context we suppose that arguments are defined by Definition 9.1 and fulfill the following two properties:
. In this context we suppose that arguments are defined by Definition 9.1 and fulfill the following two properties:(arg-ex) it is explosive in the sense that a set of sentences is inconsistent iff its consequence set is trivial; and
(arg-or)
 iff
iff  and
and  .Footnote 43
.Footnote 43

Table 7Long description
The table consists of five columns. The first column lists two knowledge bases: K subscript omega and K subscript A d. The next four columns are grouped under two headers: i-cumulativity and i-preferentiality. Under i-cumulativity: Column 2: Turnstile superscript t e m intersection P-extension. Column 3: Turnstile superscript t e m intersection A-extension. Under i-preferentiality: Column 4: Turnstile superscript t e m intersection P-extension. Column 5: Turnstile superscript t e m intersection A-extension. Row 1: K subscript omega, tick in all four consequence relation columns; each entry references Corollary Eleven point One. Row 2: K subscript A d, tick in the first three consequence relation columns, referencing Corollary Eleven point One; the fourth column also has a tick, referencing Theorem Eleven point One.
As the reader may expect, the results in this section depend also on the underlying notion of argument construction (see Fig. 24 for an overview). In the following we show that any NML based on temperate accumulation and on the argument construction in Definition 5.1 or another definition satisfying (arg-re), (arg-strict), and (arg), satisfies C ![]() (DExt) (for
(DExt) (for ![]() ) and is therefore cumulative, that is, C
) and is therefore cumulative, that is, C ![]() (
(![]() ) holds for
) holds for ![]() .
.

Figure 24 Nonmonotonic reasoning properties for temperate accumulation, where ![]() ,
, ![]() , and
, and ![]() .
.
Proposition⋆ 11.1.
Let ![]() . Given (arg), C
. Given (arg), C![]() (DExt) holds for
(DExt) holds for ![]() .
.
With Theorem 10.2 and Propositions 10.1 to 10.3 we get:
Corollary 11.1. Let ![]() and
and ![]() . Given (arg), (arg-re), and (arg-strict),
. Given (arg), (arg-re), and (arg-strict), ![]() is
is ![]() -cumulative for
-cumulative for ![]() .
.
In the presence of defeasible rules OR(![]() ) does not hold in general.
) does not hold in general.
Example 30. Let ![]() and
and ![]() with
with ![]() and
and ![]() . Clearly,
. Clearly, ![]() while
while ![]() and
and ![]() .
.
There are good news, however, for knowledge bases in ![]() ,
, ![]() is
is ![]() -preferential for
-preferential for ![]() .
.
Theorem 11.1. Let ![]() .
. ![]() is
is ![]() -preferential for
-preferential for ![]() .
.
Proof. In view of Corollary 11.1 and Lemmas 10.3 and 10.2 we only have to show OR(![]() ), where
), where ![]() . Suppose
. Suppose ![]() and
and ![]() . We show the case
. We show the case ![]() . Suppose
. Suppose ![]() and hence, by Theorem 10.1,
and hence, by Theorem 10.1, ![]() . If
. If ![]() is inconsistent in
is inconsistent in ![]() , then
, then ![]() by (arg-ex). Else, assume for a contradiction that there is a
by (arg-ex). Else, assume for a contradiction that there is a ![]() for which
for which ![]() that is consistent in
that is consistent in ![]() . So,
. So, ![]() is nontrivial and by (arg-or) so is
is nontrivial and by (arg-or) so is ![]() . So
. So ![]() which is a contradiction. So,
which is a contradiction. So, ![]() and hence, by Theorem 10.1,
and hence, by Theorem 10.1, ![]() . Thus,
. Thus, ![]() since
since ![]() . So, in any case
. So, in any case ![]() .
.
For an analogous reason ![]() . By (arg-or),
. By (arg-or), ![]() . Hence,
. Hence, ![]() . □
. □
The preceding result does not consider ![]() . We will show in Section 11.3.1 that OR(
. We will show in Section 11.3.1 that OR(![]() ) does not hold even for
) does not hold even for ![]() .
.
As a last result in this section we show that ![]() is monotonic.
is monotonic.
Proposition 11.2. ![]() (and so also CM
(and so also CM![]() and RM
and RM![]() ) hold for
) hold for ![]() .
.
Proof. Let ![]() and suppose
and suppose ![]() . Thus, there is a
. Thus, there is a ![]() for which there is an
for which there is an ![]() with
with ![]() . We have to show that
. We have to show that ![]() where
where ![]() is an arbitrary sentence. We have,
is an arbitrary sentence. We have, ![]() . So,
. So, ![]() is consistent in
is consistent in ![]() . Thus, there is a maxicon-set
. Thus, there is a maxicon-set ![]() for which
for which ![]() . We have
. We have ![]() . Thus,
. Thus, ![]() . □
. □
11.2 Alternative Characterizations
In this section we present two alternative characterizations of temperate accumulation. First, in Section 11.2.1 we show that in temperate accumulation defeasible rules are dispensable in that a given knowledge base featuring defeasible rules can be translated into one without, in such a way that extensions and consequences are preserved. In Section 11.2.2 we show that temperate accumulation can be translated into formal argumentation.
11.2.1 Naming Defaults in Temperate Accumulation
We now show that, in the context of NMLs based on temperate accumulation, every knowledge base of the form ![]() can be translated into a knowledge base of the form
can be translated into a knowledge base of the form ![]() , which gives rise to the same D- and P-extensions (Theorem 11.2). The idea is to refer (or “name”) the defaults in
, which gives rise to the same D- and P-extensions (Theorem 11.2). The idea is to refer (or “name”) the defaults in ![]() in the object language, add a strict modus ponens–like rule, and a rule that expresses that a default is defeated in case its antecedents hold but its conclusion is false. This implies that genuinely defeasible rules can be “simulated” by strict rules in systems of temperate accumulation.
in the object language, add a strict modus ponens–like rule, and a rule that expresses that a default is defeated in case its antecedents hold but its conclusion is false. This implies that genuinely defeasible rules can be “simulated” by strict rules in systems of temperate accumulation.
Suppose in the following that ![]() is a NML based on a language
is a NML based on a language ![]() with a class of associated knowledge bases
with a class of associated knowledge bases ![]() of the form of
of the form of ![]() . We assume that the notion of inconsistency underlying
. We assume that the notion of inconsistency underlying ![]() satisfies for any set of sentences
satisfies for any set of sentences ![]() the sufficient condition:
the sufficient condition: ![]() implies that
implies that ![]() is inconsistent. Our translated knowledge bases
is inconsistent. Our translated knowledge bases ![]() make use of an enriched language: every sentence in
make use of an enriched language: every sentence in ![]() is a sentence in
is a sentence in ![]() , for every
, for every ![]() ,
, ![]() and
and ![]() are sentences in
are sentences in ![]() , nothing else is a sentence in
, nothing else is a sentence in ![]() . Note that
. Note that ![]() is an object-level symbol in
is an object-level symbol in ![]() but not in
but not in ![]() . We write
. We write ![]() [resp.
[resp. ![]() ] for the set of all sentences in
] for the set of all sentences in ![]() [resp. in
[resp. in ![]() ].
].
Definition 11.1. Let the translation of a knowledge base ![]() to
to ![]() be given by:
be given by:

Note that ![]() .
.
Example 31. Recall the knowledge base from Example 9, ![]() with
with ![]() ,
, ![]() ,
, ![]() and
and ![]() . We translate it to
. We translate it to ![]() with
with
 and
and .
.
Theorem⋆ 11.2. Let ![]() be based on temperate accumulation, let
be based on temperate accumulation, let ![]() be of the form
be of the form ![]() , and let
, and let ![]() be the translation defined in Definition 11.1. Then,
be the translation defined in Definition 11.1. Then, ![]() and
and ![]() .
.
11.2.2 Temperate Accumulation as a Form of Argumentation
In the following we give an elegant argumentative characterization of NMLs based on temperate accumulation and on knowledge bases of the type ![]() .Footnote 44 We work under the assumption that (a)
.Footnote 44 We work under the assumption that (a) ![]() and
and ![]() are defined as in Definition 5.1 and (b) the inconsistency of a set of defeasible assumptions
are defined as in Definition 5.1 and (b) the inconsistency of a set of defeasible assumptions ![]() can be argumentatively expressed by
can be argumentatively expressed by
- (⋆)
 is inconsistent in
is inconsistent in  iff for every
iff for every  there is an
there is an  that concludes that the assumption
that concludes that the assumption  is false, that is,
is false, that is,  .
.
(⋆) holds if ![]() or, more generally, if
or, more generally, if ![]() for some logic
for some logic ![]() which has the property that
which has the property that ![]() is inconsistent in
is inconsistent in ![]() iff for all
iff for all ![]() ,
, ![]() .
.
Definition 11.2. We define the argumentation framework ![]() where
where ![]() for
for ![]() iff
iff ![]() for some
for some ![]() . Where
. Where ![]() , we let, moreover,
, we let, moreover, ![]() be the consequence relation induced by the X-extensions and the stable argumentation semantics (see Definition 5.2) and
be the consequence relation induced by the X-extensions and the stable argumentation semantics (see Definition 5.2) and ![]() be the set of stable A-extensions of
be the set of stable A-extensions of ![]() .
.
Example 32. We consider ![]() . An excerpt from the argumentation framework
. An excerpt from the argumentation framework ![]() is illustrated in Fig. 25. We note that
is illustrated in Fig. 25. We note that ![]() and
and ![]() .
.
We have, on the one hand, two D-extensions according to temperate accumulation, ![]() and
and ![]() , with the corresponding A-extensions
, with the corresponding A-extensions ![]() and
and ![]() and the P-extensions
and the P-extensions ![]() and
and ![]() . On the other hand, we have two stable A-extensions of
. On the other hand, we have two stable A-extensions of ![]() (highlighted in Fig. 25), namely
(highlighted in Fig. 25), namely ![]() and
and ![]() , with the corresponding P-extensions
, with the corresponding P-extensions ![]() and
and ![]() .
.

Figure 25 The argumentation framework for the knowledge base of Example 32 based on the arguments to the right. The rectangular node represents a class of arguments based on the inconsistent assumption set ![]() . An outgoing [resp. ingoing] arrow symbolizes an attack from [resp. to] some argument in the class.
. An outgoing [resp. ingoing] arrow symbolizes an attack from [resp. to] some argument in the class.
The following theorem shows that the observed correspondences are not coincidental.
Theorem 11.2. Let ![]() be an NML based on temperate accumulation for which (⋆) holds and
be an NML based on temperate accumulation for which (⋆) holds and ![]() be a knowledge base.
be a knowledge base.
1. If
 then
then  .
.2. If
 , there is a
, there is a  such that
such that  .
.
Proof. For Item 1 suppose ![]() . By Proposition 5.1,
. By Proposition 5.1, ![]() . Consider
. Consider ![]() such that
such that ![]() and
and ![]() . By (⋆) and the consistency of
. By (⋆) and the consistency of ![]() in
in ![]() ,
, ![]() . Thus,
. Thus, ![]() is conflict-free.
is conflict-free.
Let now ![]() . So, there is an
. So, there is an ![]() . Since
. Since ![]() ,
, ![]() is inconsistent in
is inconsistent in ![]() and by (⋆) there is a
and by (⋆) there is a ![]() with
with ![]() . Thus,
. Thus, ![]() .
.
For Item 2 let ![]() and
and ![]()
![]() . Clearly,
. Clearly, ![]() . Assume for a contradiction that there is an
. Assume for a contradiction that there is an ![]() . By stability, there is a
. By stability, there is a ![]() such that
such that ![]() and so
and so ![]() for some
for some ![]() . Since
. Since ![]() and
and ![]() , there is a
, there is a ![]() for which
for which ![]() and so
and so ![]() in contradiction to the conflict-freeness of
in contradiction to the conflict-freeness of ![]() . Thus,
. Thus, ![]() .
.
By Proposition 5.1, we have to show that ![]() . In view of (⋆) and the conflict-freeness of
. In view of (⋆) and the conflict-freeness of ![]() ,
, ![]() is consistent in
is consistent in ![]() . Suppose
. Suppose ![]() is such that
is such that ![]() is consistent. If
is consistent. If ![]() , then
, then ![]() and by stability, there is a
and by stability, there is a ![]() such that
such that ![]() and therefore
and therefore ![]() . But then, by (⋆),
. But then, by (⋆), ![]() is inconsistent in
is inconsistent in ![]() . So,
. So, ![]() and therefore
and therefore ![]() . □
. □
11.3 Two Families of NMLs from the Literature
In this section we will introduce two well-known families of NMLs, both based on the idea of forming maxicon sets of defeasible information from the given knowledge base.
11.3.1 Reasoning with Maxicon Sets of Sentences
A time-honored family of NMLs has been proposed by Rescher and Manor (Reference Rescher and Manor1970). These NMLs model reasoning scenarios in which an agent is confronted with reliable but not infallible information (e.g., resulting from testimonies, weather reports, and so on) that may give rise to contradictions. Such information is encoded by sets of defeasible assumptions. Clearly, due to the possibility of logical explosion, classical logic cannot be applied to such sets, at least not naively. The basic idea behind Rescher’s and Manor’s approach is to form (![]() -maximal) consistent sets of defeasible assumptions and reason on their basis. In our terminology these maxicon sets of defeasible assumptions form D-extensions and their classical closures are P-extensions induced by temperate accumulation. We obtain the three types of consequences that have been introduced in Definition 5.2.
-maximal) consistent sets of defeasible assumptions and reason on their basis. In our terminology these maxicon sets of defeasible assumptions form D-extensions and their classical closures are P-extensions induced by temperate accumulation. We obtain the three types of consequences that have been introduced in Definition 5.2.
While Rescher and Manor considered knowledge bases of the form ![]() , Makinson’s system of Default Assumptions (Makinson (Reference Makinson2005)) also considered strict assumptions and so generalized the considered class of knowledge bases to those of the form
, Makinson’s system of Default Assumptions (Makinson (Reference Makinson2005)) also considered strict assumptions and so generalized the considered class of knowledge bases to those of the form ![]() .Footnote 45 Of course, one may consider other Tarski-logics
.Footnote 45 Of course, one may consider other Tarski-logics ![]() instead of classical logic. Let the class
instead of classical logic. Let the class ![]() consist of all knowledge bases of the form
consist of all knowledge bases of the form ![]() . We let:Footnote 46
. We let:Footnote 46
1.
 iff
iff  for every
for every  .
.2.
 iff there is a
iff there is a  for which
for which  .
.3.
 iff there is a
iff there is a  such that
such that  .
.
In what follows we let arguments be defined as in Definition 9.1.
Example 33. Consider the knowledge base ![]() where
where ![]() and
and ![]() . We have
. We have ![]() where
where ![]() , and
, and ![]() . Note that the defeasible assumption
. Note that the defeasible assumption ![]() conflicts with the strict assumption
conflicts with the strict assumption ![]() .
.
We first observe that ![]() is a floating conclusion in view of the conflicting arguments
is a floating conclusion in view of the conflicting arguments ![]() and
and ![]() . Indeed,
. Indeed, ![]() while
while ![]() .
.
In view of Proposition 5.1 the three consequence relations ![]() , and
, and ![]() are identical to
are identical to ![]() , and
, and ![]() on the class
on the class ![]() . Therefore, the results from Section 11.1 are applicable (Table 8).
. Therefore, the results from Section 11.1 are applicable (Table 8).

Table 8Long description
The table consists of eleven columns. The first column lists three consequence relation types: turnstile subscript m c o n intersection P-extension, turnstile subscript m c o n intersection A-extension, and turnstile subscript m c o n union extension. The next ten columns are titled: M subscript d, M subscript s, C M subscript d, C M subscript s, C T subscript d, C T subscript s, R M subscript d, R M subscript s, O R subscript d, and O R subscript s. Row 1: Turnstile subscript m c o n intersection P-extension: tick in columns C M subscript d, C M subscript s, C T subscript d, C T subscript s, O R subscript d, and O R subscript s. Row 2: Turnstile subscript m c o n intersection A-extension: tick in columns C M subscript d, C M subscript s, C T subscript d, C T subscript s, and O R subscript s. Row 3: Turnstile subscript m c o n union extension: tick in columns M subscript d, M subscript s, R M subscript d, and R M subscript s.
Proposition 11.3. Let ![]() . Then, (i)
. Then, (i) ![]() iff
iff ![]() , (ii)
, (ii) ![]() iff
iff ![]() , and (iii)
, and (iii) ![]() iff
iff ![]() .
.
Proof. We show case (ii). The others are analogous and left to the reader. ![]() , iff, there is an
, iff, there is an ![]() with
with ![]() , iff,
, iff, ![]() , iff [by Proposition 5.1],
, iff [by Proposition 5.1], ![]() , iff,
, iff, ![]() . □
. □
In view of Corollary 11.1, Theorem 11.1 and Lemmas 10.2 and 10.3 we therefore get:
Corollary 11.2. Let ![]() .
. ![]() is
is ![]() -cumulative. If (arg-ex) and (arg-or) hold,
-cumulative. If (arg-ex) and (arg-or) hold, ![]() is
is ![]() -preferential.
-preferential.
Example 34. Where ![]() , in Table 9 we list counter-examples to (OR) and therefore to the
, in Table 9 we list counter-examples to (OR) and therefore to the ![]() -preferentiality of
-preferentiality of ![]() and
and ![]() . In Table 10 we find counterexamples to RM
. In Table 10 we find counterexamples to RM ![]() for
for ![]() .
.

Table 9Long description
The table consists of four columns: K asterisk equals, K Oplus subscript i p, K Oplus subscript i q, and K Oplus subscript i (p or q). It read as follows: Row 1: i equals s, K equals K subscript 1: maxcon (K asterisk); {not q and r}; {not p and r}; {not q and r}, {not p and r}. Row 2: i equals s, K equals K subscript 1: intersection D-extension (K asterisk); {not q not r}; {not p not r}; empty set. Row 3: i equals s, K equals K subscript 1: K asterisk turnstile superscript mcon subscript A-extension r question mark; checkmark; checkmark; cross. Row 4: i equals d, K equals K subscript 2: maxcon (K asterisk); A subscript 2 superscript p backslash {not p} and below it A subscript 2; A subscript 2 superscript p backslash {not q} and below it A subscript 2; A subscript 2 superscript p or q backslash {not p} and below it A subscript 2 superscript p or q backslash {not q} and below it A subscript 2. Row 5: i equals d, K equals K subscript 2: intersection D-extension (K asterisk); A subscript 2 backslash {not p}; A subscript 2 backslash {not q}; A subscript 2 backslash {not p, not q}. Row 6: i equals d, K equals K subscript 2: K asterisk turnstile superscript mcon subscript A-extension r question mark; checkmark; checkmark; cross. Row 7: i is an element of {s, d}, K equals K subscript 3: maxcon (K asterisk); A subscript 3 superscript u Oplus subscript i p and below it A subscript 3 superscript not u Oplus subscript i p; A subscript 3 superscript u Oplus subscript i q and below it A subscript 3 superscript not u Oplus subscript i q; A subscript 3 superscript u Oplus subscript i (p or q) and below it A subscript 3 superscript not u Oplus subscript i (p or q). Row 8: i is an element of {s, d}, K equals K subscript 3: K asterisk turnstile superscript mcon subscript U-extension r question mark; checkmark; checkmark; cross.

Table 10Long description
The table consists of four columns: K asterisk equals, K, K oplus subscript s not (p and r), and K oplus subscript d not (p and r). It reads as follows: Row 1: maxcon of K asterisk; set of p, q and r; set of not p, q and r; set of p; set of not p, q and r; set of p, not (p and r); set of p, q and r; set of not p, q and r, not (p and r). Row 2: intersection D-extension of K asterisk; set of q and r; empty set; empty set. Row 3: K asterisk turnstile superscript m c o n subscript intersection A-extension r question mark; tick; cross; cross. Row 4: K asterisk not turnstile superscript m c o n subscript intersection A-extension not (p and r) question mark; tick; blank; blank. Row 5: K asterisk turnstile superscript m c o n subscript intersection P-extension r question mark; tick; cross; cross. Row 6: K asterisk not turnstile superscript m c o n subscript intersection P-extension not (p and r) question mark; tick; blank; blank.
We end this section with two simple counterexamples concerning the cautious monotonicity and transitivity of ![]() and a positive result concerning its rational monotonicity.
and a positive result concerning its rational monotonicity.
Example 35. Let ![]() . We first let
. We first let ![]() . Then,
. Then, ![]() and
and ![]() , but
, but ![]() . Note for this that
. Note for this that ![]() . This shows that CM
. This shows that CM ![]() and M
and M ![]() don’t hold.
don’t hold.
Let now ![]() and
and ![]() . We note that
. We note that ![]() (since
(since ![]() ) and
) and ![]() (since
(since ![]() ). However,
). However, ![]() . This shows that CT
. This shows that CT ![]() does not hold.
does not hold.
Proposition 11.4. Let ![]() ,
, ![]() , and
, and ![]() . Then, RM
. Then, RM![]() holds.
holds.
Sketch of the Proof. Suppose ![]() and
and ![]() and let
and let ![]() . In view of
. In view of ![]() every
every ![]() is consistent with
is consistent with ![]() . It is therefore easy to see that
. It is therefore easy to see that ![]() iff
iff ![]() and therefore also
and therefore also ![]() .
.
11.3.2 Reasoning with Consistent Sets of Defaults and Metarules: Input–Output Logic
Input–output logics (in short, IO-logics) have been first presented in Makinson and Van Der Torre (Reference Makinson and Van Der Torre2000) and in a nonmonotonic setting in Reference Makinson and Van Der Torre2001. We work with the class of knowledge bases ![]() of the type
of the type ![]() , where the strict rules are provided by a Tarski base logic
, where the strict rules are provided by a Tarski base logic ![]() (such as classical or intuitionistic logic).Footnote 47 Instead of Definitions 5.1, arguments in IO-logic are constructed according to the following “two-phase” definition in which (a) the derivation of information from strict assumptions by the strict rules and (b) the derivation of defeasible rules from strict and defeasible rules by means of metarules are separated. The detachment of argument conclusions is applied to the results of (a) and (b).
(such as classical or intuitionistic logic).Footnote 47 Instead of Definitions 5.1, arguments in IO-logic are constructed according to the following “two-phase” definition in which (a) the derivation of information from strict assumptions by the strict rules and (b) the derivation of defeasible rules from strict and defeasible rules by means of metarules are separated. The detachment of argument conclusions is applied to the results of (a) and (b).
Definition 11.3 (Arguments, Consistency, and Consequences in IO-logic). Let ![]() . Where
. Where ![]() ,
, ![]() iff (a)
iff (a) ![]() and (b)
and (b) ![]() . We let
. We let ![]() and
and ![]() .
.
![]() is consistent in
is consistent in ![]() iff there is no sentence
iff there is no sentence ![]() for which
for which ![]() .
.
We define D-, A-, and P-extensions as usual (see Section 10). Where ![]() , we will write
, we will write ![]() for the induced consequence relation (see Definition 5.2) on the class of knowledge bases
for the induced consequence relation (see Definition 5.2) on the class of knowledge bases ![]() .
.
In IO-logic metarules play a central role. Paradigmatic rules are:

Table 07Long description
The Paradigmatic rules are: 1. Right Weakening (RW); (A right arrow B), (C implies A) turnstile (C implies B). 2. Left Strengthening (LS): (A right arrow C), (C implies B) turnstile (A implies B). 3. Right Conjunction (AND): (A implies B), (A implies C) turnstile (A implies B and C). 4. Cumulative Transitivity (CT): (A implies B), (A and B implies C) turnstile (A implies C). 5. Left Disjunction (OR): (A implies C), (B implies C) turnstile (A or B implies C). 6. Identity (ID): Turnstile A implies A.
Depending on the underlying class of knowledge bases, we have 12 base systems, summarized in Fig. 26.

Figure 26 The basic input–output logics and their associated knowledge bases where ![]() and
and ![]() .
.
Example 36. Let ![]() where
where ![]() ,
, ![]() , and
, and ![]() . We have three maxicon sets for
. We have three maxicon sets for ![]() :
: ![]() ,
, ![]() , and
, and ![]() . By Proposition 5.1, we know that these correspond to the D-extension generated by TemAcc. We have
. By Proposition 5.1, we know that these correspond to the D-extension generated by TemAcc. We have ![]() since
since ![]() doesn’t contain an argument for
doesn’t contain an argument for ![]() .
.
Note that ![]() is not consistent since it contains the argument
is not consistent since it contains the argument ![]() for
for ![]() and
and ![]() for
for ![]() based on the
based on the ![]() -derivation
-derivation 
IO-logics have found applications in deontic logic where the rules in ![]() are interpreted as conditional norms:
are interpreted as conditional norms: ![]() is read as “
is read as “![]() commits us/you/etc. to bring about
commits us/you/etc. to bring about ![]() ” (Parent & van der Torre, Reference Parent, van der Torre, Gabbay, Horty, Parent, van der Meyden and van der Torre2013). The right side of the consequence relation
” (Parent & van der Torre, Reference Parent, van der Torre, Gabbay, Horty, Parent, van der Meyden and van der Torre2013). The right side of the consequence relation ![]() encodes the obligations derivable from a knowledge base, where the latter represents the information available about the actual situation
encodes the obligations derivable from a knowledge base, where the latter represents the information available about the actual situation ![]() and the given conditional norms
and the given conditional norms ![]() . In deontic logic, conflicts between norms can occur in various ways, for example, in terms of contrary-to-duty situations.
. In deontic logic, conflicts between norms can occur in various ways, for example, in terms of contrary-to-duty situations.
Example 37. Let ![]() stand for “helping the neighbor,” and
stand for “helping the neighbor,” and ![]() for “notifying the neighbor” (Chisholm, Reference Chisholm1963). Consider
for “notifying the neighbor” (Chisholm, Reference Chisholm1963). Consider ![]() ,
, ![]() and
and ![]() . We have three maxicon sets, namely
. We have three maxicon sets, namely ![]() ,
, ![]() , and
, and ![]() . One may object to
. One may object to ![]() being part of the D-extensions since our strict assumptions express that our agent already determined the outcome
being part of the D-extensions since our strict assumptions express that our agent already determined the outcome ![]() and so
and so ![]() would not be action-guiding. Moreover, in
would not be action-guiding. Moreover, in ![]() this leads to a pragmatic oddity according to which an agent should help and also not notify the neighbor. To deal with this problem, knowledge bases have been extended with a set of constraints (such as here
this leads to a pragmatic oddity according to which an agent should help and also not notify the neighbor. To deal with this problem, knowledge bases have been extended with a set of constraints (such as here ![]() ) on the output in Makinson and Van Der Torre (Reference Makinson and Van Der Torre2001). In order to simplify the presentation, we have omitted constraints in this section.
) on the output in Makinson and Van Der Torre (Reference Makinson and Van Der Torre2001). In order to simplify the presentation, we have omitted constraints in this section.
We will now consider some of the properties studied in Section 10.3. We say that ![]() has a proper conjunction
has a proper conjunction ![]() iff (a)
iff (a) ![]() iff
iff ![]() and (b)
and (b) ![]() , …,
, …, ![]() implies
implies ![]() . In the following we assume that
. In the following we assume that ![]() has a proper conjunction.
has a proper conjunction.
Lemma 11.1. An IO-logic whose metarules include LS and CT satisfies (arg-re) and (arg).
Proof. For (arg-trans) consider a ![]() for which there is an
for which there is an ![]() and suppose
and suppose ![]() . Thus, there are proofs
. Thus, there are proofs ![]() resp.
resp. ![]() based on the rules in
based on the rules in ![]() of
of ![]() resp. of
resp. of ![]() from
from ![]() . Moreover,
. Moreover, ![]() and
and ![]() . So, there are
. So, there are ![]() for which
for which ![]() . By the monotonicity of
. By the monotonicity of ![]() and since
and since ![]() is a proper conjunction,
is a proper conjunction, ![]() and
and ![]() . Consider the following proof based on the metarules
. Consider the following proof based on the metarules ![]() :
:

Note that ![]() and so
and so ![]() .
.
The simple proofs of (arg-re) and (arg-mono) are left to the reader. □
By Lemma 11.1, Propositions 10.2 and 11.1, and Theorem 10.2 we get:
Corollary 11.3. Let ![]() . Any IO-logic whose metarules include LS and CT satisfies C
. Any IO-logic whose metarules include LS and CT satisfies C![]() and LLE
and LLE![]() .
.
In view of Corollary 11.1 the logics ![]() with
with ![]() from Fig. 26 are
from Fig. 26 are ![]() -cumulative, since their notions of argument satisfy (arg-strict).
-cumulative, since their notions of argument satisfy (arg-strict).
Lemma 11.2. Any IO-logic ![]() from Fig. 26 satisfies (arg-strict).
from Fig. 26 satisfies (arg-strict).
Proof. Concerning (i) we note that if ![]() , since
, since ![]() , also
, also ![]() . Concerning (ii), where
. Concerning (ii), where ![]() , suppose
, suppose ![]() and there are
and there are ![]() . So,
. So, ![]() for each
for each ![]() . So,
. So, ![]() where
where ![]() . By (LS),
. By (LS), ![]() for each
for each ![]() . By AND,
. By AND, ![]() where
where ![]() . Since
. Since ![]() and by RW,
and by RW, ![]() . □
. □
By Corollary 11.1 and Lemmas 11.1 and 11.2 we get:
Corollary 11.4. Let ![]() and
and ![]() .
. ![]() satisfies
satisfies ![]() -cumulativity for
-cumulativity for ![]() .
.
Example 38. ![]() -cumulativity is not satisfied for
-cumulativity is not satisfied for ![]() since Ref does not hold. Consider
since Ref does not hold. Consider ![]() . Clearly, there are maxicon sets including
. Clearly, there are maxicon sets including ![]() in view of which
in view of which ![]() , where
, where ![]() .
.
The situation is different when considering ![]() . Now, the only D-extension is
. Now, the only D-extension is ![]() and therefore
and therefore ![]() since
since ![]() due to the presence of the metarule
due to the presence of the metarule ![]() .
.
The following example demonstrates that the OR metarule allows for a form of disjunctive reasoning that is not available in systems without.
Example 39. Let ![]() , where
, where ![]() and
and ![]() . Note that
. Note that ![]() in view of the proof:
in view of the proof: ![]() (by OR and LS) and
(by OR and LS) and ![]() by CT. Note also that
by CT. Note also that ![]() is consistent. Therefore,
is consistent. Therefore, ![]() and
and ![]() . The situation is different for weaker logics; for example, if we let
. The situation is different for weaker logics; for example, if we let ![]() where
where ![]() and
and ![]() , then
, then ![]() and so
and so ![]() and
and ![]() .
.
If OR is available, we get OR ![]() for base logics that satisfy (arg-or) and (arg-ex) (such as
for base logics that satisfy (arg-or) and (arg-ex) (such as ![]() , see Section 11.1).
, see Section 11.1).
Proposition 11.5. Let ![]() and
and ![]() . If (arg-or) and (arg-ex), we have OR
. If (arg-or) and (arg-ex), we have OR![]() for
for ![]() .
.
Proof. Let ![]() . Suppose
. Suppose ![]() and
and ![]() and consider
and consider ![]() . Assume for a contradiction that
. Assume for a contradiction that ![]() is inconsistent in both
is inconsistent in both ![]() and
and ![]() . So, there are
. So, there are ![]() and
and ![]() . By (arg-ex) and LS,
. By (arg-ex) and LS, ![]() for some
for some ![]() . By (arg-or),
. By (arg-or), ![]() . So, by OR,
. So, by OR, ![]() . This shows that
. This shows that ![]() is inconsistent in
is inconsistent in ![]() , which is a contradiction.
, which is a contradiction.
So, ![]() or
or ![]() . Without loss of generality, assume the former. Thus, there is a
. Without loss of generality, assume the former. Thus, there is a ![]() for which
for which ![]() . Assume for a contradiction that
. Assume for a contradiction that ![]() is inconsistent in
is inconsistent in ![]() . So, there are
. So, there are ![]() . Since
. Since ![]() and by (arg-or), also
and by (arg-or), also ![]() . But then
. But then ![]() is not consistent in
is not consistent in ![]() , which is a contradiction. So,
, which is a contradiction. So, ![]() is consistent in
is consistent in ![]() and by the
and by the ![]() -maximally of
-maximally of ![]() ,
, ![]() . Since
. Since ![]() ,
, ![]() .
.
Altogether this shows that ![]() . □
. □
An immediate consequence of Corollary 11.4 and Proposition 11.5 is:Footnote 48
Corollary 11.5. Let ![]() . If (arg-or) and (arg-ex),
. If (arg-or) and (arg-ex), ![]() satisfies
satisfies ![]() -preferentiality for
-preferentiality for ![]() .
.
12 Greedy Accumulation: Properties and Reiter’s Default Logic
In this section we take a closer look at greedy accumulation. We start by considering some of the properties of nonmonotonic inference for greedy accumulation in Section 12.1. We then investigate Reiter’s more general formulation of default rules in Section 12.2. In Section 12.3 we show that default logic can be considered a form of formal argumentation.
12.1 Properties of Nonmonotonic Reasoning
As we have seen in Section 10.3, some properties of nonmonotonic inference (Propositions 10.1 to 10.3, in particular CT, LLE, Ref, and RW) hold for greedy accumulation. In this section we present some negative results.
Example 40 (Makinson, 2003). We consider the default theory

We get one D-extension, namely ![]() with corresponding P-extension
with corresponding P-extension ![]() and so
and so ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
When considering ![]() resp.
resp. ![]() the situation changes. We now have the additional D-extension
the situation changes. We now have the additional D-extension ![]() resp.
resp. ![]() with the corresponding P-extension
with the corresponding P-extension ![]() . Thus, where
. Thus, where ![]() ,
, ![]() and
and ![]() .
.
The example shows that CM does not hold for greedy accumulation. The next example shows that also OR fails (it is analogous to Example 30 for temperate accumulation).
Example 41. Let ![]() ,
, ![]() , and
, and

We note that ![]() and
and ![]() , although
, although ![]() (since the only D-extension of
(since the only D-extension of ![]() is
is ![]() ).
).
It is not surprising that several alternative formulations of default logic have been introduced to obtain CT or OR, a discussion of which goes beyond the scope of this Element (see Section 12.3).
12.2 Nonnormal Defaults
Reiter’s default logic is one of the most prominent NMLs to reason with default rules such as “Birds usually fly.” In Reiter’s original account defaults are more expressive in the sense that they allow one to express additional consistency assumptions. They have the following general form:
 (12.2.1)
(12.2.1)
Besides the body ![]() and a head
and a head ![]() , each default rule also comes with justifications
, each default rule also comes with justifications ![]() . Where
. Where ![]() is a set of generalized defaults we call knowledge bases of the form
is a set of generalized defaults we call knowledge bases of the form ![]() Reiter default theories.Footnote 49
Reiter default theories.Footnote 49
Example 42. We compare the following two defaults:

Defaults of the form ![]() , for which the justification is identical to the conclusion, are called normal defaults. Both,
, for which the justification is identical to the conclusion, are called normal defaults. Both, ![]() and
and ![]() have the same conditions of defeat: defeat happens if we learn that a person is not guilty or not suspect. However,
have the same conditions of defeat: defeat happens if we learn that a person is not guilty or not suspect. However, ![]() has a weaker conclusion in that it only allows one to infer that the person who has a motive is suspect, but unlike
has a weaker conclusion in that it only allows one to infer that the person who has a motive is suspect, but unlike ![]() it does not warrant the inference to the person’s guilt as well. The use of nonnormal defaults is motivated by cases in which the conclusion is logically weaker than the justification. From the perspective of argumentation these are cases in which we do not only want to retract inferences when being rebutted, but also allow other forms of defeat which are expressed in terms of richer justifications (one may think of these justifications as anchors for undercuts).
it does not warrant the inference to the person’s guilt as well. The use of nonnormal defaults is motivated by cases in which the conclusion is logically weaker than the justification. From the perspective of argumentation these are cases in which we do not only want to retract inferences when being rebutted, but also allow other forms of defeat which are expressed in terms of richer justifications (one may think of these justifications as anchors for undercuts).
Definition 12.1. Let ![]() be a Reiter default theory and
be a Reiter default theory and ![]() . We let
. We let ![]() and
and ![]() be defined similar to Definition 5.1:
be defined similar to Definition 5.1: ![]() iff
iff
 , where
, where  . We let
. We let  ,
,  , and
, and  .
. , where
, where  ,
,  , and
We let
, and
We let
 ,
,  , and
, and  .
. , where
, where  ,
,  , and
, and  .
.We let
 ,
,  , and
, and  .
.
Where ![]() and
and ![]() , we let
, we let ![]() and
and ![]() . We let
. We let ![]() be the set of all
be the set of all ![]() such that for all
such that for all ![]() there is an
there is an ![]() with
with ![]() . Where
. Where ![]() is a set of
is a set of ![]() -sentences, we let
-sentences, we let ![]() be the set of all
be the set of all ![]() for which each
for which each ![]() is consistent with
is consistent with ![]() . We let
. We let ![]() .
.
D-extensions of Reiter default theories are generated by an algorithm, similar to GreedyAcc. However, we need to accommodate the consistency check (in the loop guard, line 3) to the additional ingredient of defaults, their justifications. Since justifications need not be implied by the heads of their respective defaults, the consistency check cannot proceed iteratively anymore. This is to avoid that a justification of a default added earlier conflicts with the head of one added later on in the procedure. Reiter solved this problem by means of a semi-inductive procedure in which the reasoner has to first guess the outcome. Consistency checks are then performed relative to the guessed set of sentences. This results in the algorithm GreedyAccGen.Footnote 50

Algorithm 5Long description
The Algorithm displays code in twelve lines: 1. procedure Generalized Greedy Accumulation (K, D): where K equals A subscript s, R subscript d, R subscript s and D is a subset of R subscript d. 2. D asterisk left arrow empty set: init. 3. E left arrow Con [Arg subscript K (D)]: the guessed P-extension. 4. while exists r in Trig superscript T subscript K (E, D asterisk) backslash D do: scan triggered and consistent defaults. 5. D asterisk left arrow D asterisk union {r}: update scenario. 6. end while: no more triggered and consistent defaults. 7. if D equals D asterisk then. 8. return (D asterisk): correct guess. 9. else. 10. return(failure): incorrect guess. 11. end if. 12. end procedure.
Definition 12.2. A Reiter D-extension of a Reiter default theory ![]() is a set
is a set ![]() for which
for which ![]() . Its corresponding A-extension is
. Its corresponding A-extension is ![]() , and its corresponding P-extension is
, and its corresponding P-extension is ![]() . We write again
. We write again ![]() [resp.
[resp. ![]() ,
, ![]() ] for the set of Reiter D- [resp. A-,P-]extensions of
] for the set of Reiter D- [resp. A-,P-]extensions of ![]() .
.
Example 43. We consider ![]() , where
, where

We simulate two runs of GreedyAccGen.
1. When running GreedyAccGen
 ,
,  is the set
is the set  closed under classical logic. In the first round of the while-loop we add
closed under classical logic. In the first round of the while-loop we add  to
to  . In the second round we add
. In the second round we add  since its justification is also consistent with
since its justification is also consistent with  . This leads to failure since
. This leads to failure since  .
.2. We consider GreedyAccGen
 . Now
. Now  is the set
is the set  closed under classical logic. Since
closed under classical logic. Since  is inconsistent with
is inconsistent with  , the loop terminates with
, the loop terminates with  and therefore returns the only D-extension of
and therefore returns the only D-extension of  .
.
Reiter’s format of defaults and the GreedyAccGen algorithm generalize greedy accumulation as presented in Section 5.2.1. Suppose we have a knowledge base ![]() with only defaults of the form
with only defaults of the form ![]() . We can translate
. We can translate ![]() to a Reiter default theory
to a Reiter default theory ![]() by translating each default
by translating each default ![]() to a Reiter default
to a Reiter default

Applying GreedyAcc to ![]() and GreedyAccGen to
and GreedyAccGen to ![]() will lead to the same D-extensions (under the translation) and therefore the same P-extensions (Łukaszewicz, Reference Łukaszewicz1988).
will lead to the same D-extensions (under the translation) and therefore the same P-extensions (Łukaszewicz, Reference Łukaszewicz1988).
Nevertheless, the introduction of generalized defaults may lead to scenarios in which no D-extensions exist.
Example 44. Consider ![]() where
where ![]() and
and ![]() only contains the default
only contains the default ![]() . We have two possible guesses to run GreedyAccGen:
. We have two possible guesses to run GreedyAccGen: ![]() and
and ![]() . Note that with the first guess the algorithm never enters the while-loop, since the justification
. Note that with the first guess the algorithm never enters the while-loop, since the justification ![]() of
of ![]() is inconsistent with
is inconsistent with ![]() and it therefore returns failure. With the second guess, however, since
and it therefore returns failure. With the second guess, however, since ![]() is consistent with
is consistent with ![]() , the while-loop is entered and
, the while-loop is entered and ![]() is added to
is added to ![]() , again leading to failure.
, again leading to failure.
Similarly as described in Section 10.2 for normal default theories, also Reiter D-extensions can be characterized in terms of fixed-points.
Proposition⋆ 12.1. Let ![]() be a Reiter default theory,
be a Reiter default theory, ![]() , and
, and ![]() .
. ![]() is a Reiter D-extension of
is a Reiter D-extension of ![]() iff
iff ![]() .
.
12.3 An Argumentative Characterization of Reiter’s Default Logic
In this section we demonstrate that there is a natural argumentative characterization of extensions of Reiter default theories.Footnote 51 For this we use a slightly generalized language ![]() . The unary operator
. The unary operator ![]() will track the consistency assumptions underlying the justifications in generalized defaults. For this, it need not get equipped with logical properties, but it will be used when defining argumentative attacks.
will track the consistency assumptions underlying the justifications in generalized defaults. For this, it need not get equipped with logical properties, but it will be used when defining argumentative attacks.
Definition 12.3. Given a Reiter default theory ![]() , we define the argumentation framework
, we define the argumentation framework ![]() , where
, where ![]() ,
, ![]() ,
, ![]() contains
contains ![]() for every sentence
for every sentence ![]() , and
, and ![]() ,
, ![]() iff
iff
 (12.2.1)
(12.2.1)
We let ![]() if there is a
if there is a ![]() such that
such that ![]() , where
, where ![]() for all sentences
for all sentences ![]() .
.
Example 45 (Ex. 43 cont.). We recall ![]() from Example 43. In Fig. 27 we see an excerpt of
from Example 43. In Fig. 27 we see an excerpt of ![]() . The only Reiter D-extension of
. The only Reiter D-extension of ![]() is
is  . Its induced P-extension corresponds exactly to the consequences of the arguments in the only stable A-extension of
. Its induced P-extension corresponds exactly to the consequences of the arguments in the only stable A-extension of ![]() (highlighted).
(highlighted).

Figure 27 Illustration of Example 45.
The following result shows that the correspondence between Reiter extensions and stable A-extensions is not coincidental.
Theorem⋆ 12.1 Let ![]() be a general default theory and
be a general default theory and ![]() as in Definition 12.3. Then
as in Definition 12.3. Then
1. for every Reiter P-extension
 of
of  , there is a stable A-extension
, there is a stable A-extension  of
of  for which
for which  ,
,2. for every stable A-extension
 of
of  ,
,  is a Reiter P-extension of
is a Reiter P-extension of  .
.
Selected Further Readings
Metatheoretic properties of reasoning on the basis of maxicon sets in the style of Rescher and Manor have been thoroughly studied in Benferhat et al. (Reference Benferhat, Dubois and Prade1997). A well-known prioritized version is provided in Brewka (Reference Brewka1989). An overview on the state of the art in input–output logic can be found in Parent and van der Torre (Reference Parent, van der Torre, Gabbay, Horty, Parent, van der Meyden and van der Torre2013). Input–output logics have also been applied to causal and explanatory reasoning in many works by Bochman: Bochman (Reference Bochman2005) is a good starting point. Proof theories for input–output logics that allow for Boolean combinations of defeasible conditionals are presented in Straßer et al. (Reference Straßer, Beirlaen and Van De Putte2016) and van Berkel and Straßer (Reference van Berkel, Straßer, Toni, Polberg, Booth, Caminada and Kido2022). The latter also provides a translation of input/output logic to formal argumentation. Hansen’s approach to (prioritized) deontic conditionals falls within temperate accumulation (Hansen, Reference Hansen2008), while Horty’s follows the greedy approach of deontic logic (Horty, Reference Horty2012).
An overview on many variants of default logic can be found in Antoniou and Wang (Reference Antoniou, Wang, Gabbay and Woods2009). Due to the problems indicated in Section 12.1, some cumulative variants have been proposed (Antonelli, Reference Antonelli1999; Brewka, Reference Brewka1991) as well as disjunctive versions (Gelfond et al., Reference Gelfond, Lifschitz, Przymusinska and Truszczynski1991). In Poole (Reference Poole1985) special attention is paid to specificity.
Moore’s autepistemic logic has close links to default logic (Denecker et al., Reference Denecker, Marek and Truszczynski2011; Konolige, Reference Konolige1988) and to logic programming (Gelfond & Lifschitz, Reference Gelfond and Lifschitz1988). The equi-expressivity of adaptive logics and default assumptions have been shown in Van De Putte (Reference Van De Putte2013). A modal selection semantics (as presented in Sections 5.3 and Section 15) for default logic has been studied in Lin and Shoham (Reference Lin and Shoham1990).
Part IV Semantic Methods
In this final part of the Element we move the focus from syntax to semantics. The main underlying method will be based on imposing preference orders on interpretations and selecting specific interpretations of the given information. In Section 13 we will study a well-known semantics for defaults (Kraus et al., Reference Kraus, Lehman and Magidor1990) based on the idea of preferring more “normal” models over less “normal” ones. In particular, we investigate a sophisticated method to determine the set of defaults that are entailed by a given set of defaults, the Rational Closure (Lehmann & Magidor, Reference Lehmann and Magidor1992). Section 14 provides an overview on some quantitative methods for providing meaning to defaults, including probabilistic methods. In Section 15 we use the idea of ordering models to obtain a semantics for temperate accumulation. Finally, in Section 16 we introduce one of the central paradigms in logic programming, answer set programming, and show how it is closely related to both default logic and formal argumentation. In this way, we once more demonstrate that although the underlying formal methods of NMLs are quite diverse, they often result in the same consequence relations and extensions (recall Fig. 14).
13 A Semantics for Defaults
In Section 1.1 we proposed to interpret defaults ![]() as “If
as “If ![]() then normally/typically/usually/etc.
then normally/typically/usually/etc. ![]() ”. The argumentation (Part II) and accumulation methods (Part III) model reasoning with defaults by focusing on inference rules: arguments are formed by treating
”. The argumentation (Part II) and accumulation methods (Part III) model reasoning with defaults by focusing on inference rules: arguments are formed by treating ![]() as a defeasible inference rule and the notions of consistency and conflict are used to obtain nonmonotonic consequence relations. In this way the meaning of
as a defeasible inference rule and the notions of consistency and conflict are used to obtain nonmonotonic consequence relations. In this way the meaning of ![]() is characterized in a syntax-based, proof-theoretic way.
is characterized in a syntax-based, proof-theoretic way.
In what follows, we will interpret ![]() in a semantic, model-theoretic way, by:
in a semantic, model-theoretic way, by:
- (⋆)
 holds under the most normal/plausible/etc. situations in which
holds under the most normal/plausible/etc. situations in which  holds.
holds.
This interpretation naturally leads to nonmonotonicity: while Anne jogs most mornings (![]() ), rainy mornings are exceptional (
), rainy mornings are exceptional (![]() ).
).
The proposed interpretation can be made precise by using models of the form ![]() with a nonempty set of situations
with a nonempty set of situations ![]() which are interpreted by means of an assignment function
which are interpreted by means of an assignment function ![]() that associates atoms with the set of those situations (also referred to as states) in which they hold, and an order
that associates atoms with the set of those situations (also referred to as states) in which they hold, and an order ![]() that orders situations according to their normality. We read
that orders situations according to their normality. We read ![]() (where
(where ![]() ) as expressing that
) as expressing that ![]() is less normal than
is less normal than ![]() . Where
. Where ![]() we let
we let

 for an atom
for an atom  iff
iff 
 iff
iff 
 iff
iff  and
and 
 iff
iff  or
or  .
.
We let ![]() be the set of all situations which validate
be the set of all situations which validate ![]() and skip the subscript whenever the context disambiguates. Such sets of situations are called propositions. Following the idea expressed in (⋆), we let:Footnote 52
and skip the subscript whenever the context disambiguates. Such sets of situations are called propositions. Following the idea expressed in (⋆), we let:Footnote 52
 iff in all
iff in all  ,
,  .
.
Note that validity for ![]() is defined globally, not relative to a given state. In the following we write
is defined globally, not relative to a given state. In the following we write ![]() for the set of all
for the set of all ![]() for which
for which ![]() , and we write
, and we write ![]() in case
in case ![]() . We will call
. We will call ![]() the conditional theory induced by
the conditional theory induced by ![]() .
.
By letting ![]() we can express that
we can express that ![]() is “more normal” than
is “more normal” than ![]() . Indeed, if in all minimal states of
. Indeed, if in all minimal states of ![]() ,
, ![]() holds, then the minimal states of
holds, then the minimal states of ![]() are
are ![]() -lower than those of
-lower than those of ![]() .
.
One may think of ![]() as a model of the belief state of an agent.
as a model of the belief state of an agent. ![]() expresses that if the agent were to learn
expresses that if the agent were to learn ![]() , she would believe
, she would believe ![]() , where
, where ![]() means that, absent new information, the agent believes
means that, absent new information, the agent believes ![]() . If
. If ![]() , the agent would be less surprised when learning
, the agent would be less surprised when learning ![]() than when learning
than when learning ![]() .
.
Example 46. Let ![]() where
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We have, for instance,
. We have, for instance, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus,
. Thus,
1.
 and
and  ,
,2.
 and so
and so  ,
,3. but
 and
and  .
.
In models with infinite sequences of more and more normal states we may face situations in which ![]() is empty, although
is empty, although ![]() is not. To exclude such scenarios, we restrict the focus on only those models for which it holds that for all sentences
is not. To exclude such scenarios, we restrict the focus on only those models for which it holds that for all sentences ![]() and all
and all ![]() there is an
there is an ![]() such that
such that ![]() . Models that satisfy this requirement are called smooth (Kraus et al., Reference Kraus, Lehman and Magidor1990) or stuttered (Makinson, Reference Makinson2003). In what follows we will discuss some other basic properties one may impose on
. Models that satisfy this requirement are called smooth (Kraus et al., Reference Kraus, Lehman and Magidor1990) or stuttered (Makinson, Reference Makinson2003). In what follows we will discuss some other basic properties one may impose on ![]() , such as transitivity (if
, such as transitivity (if ![]() and
and ![]() , then also
, then also ![]() ) or irreflexivity (
) or irreflexivity (![]() ).
).
In particular, we will study two classes of well-behaved models by only considering models for which the underlying order ![]() has specific properties.
has specific properties.
13.1 Preferential Models
Let us now state properties one may expect from the conditional theory ![]() induced by a model
induced by a model ![]() . For this, we adjust the properties from Section 4 to statements of the form
. For this, we adjust the properties from Section 4 to statements of the form ![]() .
.
The properties are to be read as closure conditions on a set of defaults ![]() . For example, REF states that
. For example, REF states that ![]() for all sentences
for all sentences ![]() , or CM states that if
, or CM states that if ![]() , then also
, then also ![]() for all sentences
for all sentences ![]() .
.

Table 08Long description
The list of logical properties includes: 1. Left Logical Equivalence (LLE): If turnstile subscript CL A equivalence B, then A implies C iff B implies C. 2. Right Weakening (RW): If A turnstile subscript CL B and C implies A implies C implies B. 3. Reflexivity (Ref): A implies A. 4. Constructive Dilemma (OR): If A implies C and B implies C, then A or B implies C. 5. Cautious Monotonicity (CM): If A implies B and A implies C, then A and B implies C. 6. Cautious Transitivity (CT); If A implies B and A and B implies C, then A implies C.
We call a set of defaults ![]() preferential theory in case it is closed under these properties.
preferential theory in case it is closed under these properties.
Given the intuitive nature of the previously mentioned properties, a natural question is: what kinds of models give rise to preferential theories? With Kraus et al. (Reference Kraus, Lehman and Magidor1990) we call ![]() a preferential model in case
a preferential model in case ![]() is smooth, irreflexive, and transitive. It is an easy exercise to confirm that the preceding properties hold for
is smooth, irreflexive, and transitive. It is an easy exercise to confirm that the preceding properties hold for ![]() , where
, where ![]() is a preferential model. We paradigmatically consider CM (for which smoothness is needed) and OR.
is a preferential model. We paradigmatically consider CM (for which smoothness is needed) and OR.
For CM, suppose that ![]() and
and ![]() . In case
. In case ![]() , trivially
, trivially ![]() . Otherwise, consider some
. Otherwise, consider some ![]() . Assume for a contradiction that
. Assume for a contradiction that ![]() . Thus, by smoothness, there is a
. Thus, by smoothness, there is a ![]() such that
such that ![]() . Since
. Since ![]() and
and ![]() ,
, ![]() and so
and so ![]() . But then
. But then ![]() was not
was not ![]() -minimal in
-minimal in ![]() , a contradiction. So,
, a contradiction. So, ![]() and so
and so ![]() since
since ![]() . Thus,
. Thus, ![]() .
.
For OR suppose that ![]() and
and ![]() . If
. If ![]() , trivially
, trivially ![]() . Otherwise consider an
. Otherwise consider an ![]() . Assume for a contradiction that
. Assume for a contradiction that ![]() . Then, there is a
. Then, there is a ![]() such that
such that ![]() . Since
. Since ![]() , this contradicts the
, this contradicts the ![]() -minimality of
-minimality of ![]() . So,
. So, ![]() and so, by the supposition,
and so, by the supposition, ![]() . So,
. So, ![]() .
.
Altogether, it can be shown that:
Theorem 13.1 (Kraus et al., 1990). If ![]() is a preferential model,
is a preferential model, ![]() is a preferential theory.
is a preferential theory.
Also the inverse holds, that is, any preferential ![]() can be characterized by a preferential model. As a result, preferential models provide an adequate semantic characterization of preferential theories.
can be characterized by a preferential model. As a result, preferential models provide an adequate semantic characterization of preferential theories.
Theorem 13.2 (Kraus et al., 1990). If ![]() is a preferential theory, then there is a preferential model
is a preferential theory, then there is a preferential model ![]() for which
for which ![]() .
.
13.2 Ranked Models
Preferential models do not, in general, validate the rational monotonicity property:Footnote 53
| RM | If |
RM has in ![]() a negative condition. A set of defaults
a negative condition. A set of defaults ![]() is closed under RM if for all sentences
is closed under RM if for all sentences ![]() , if
, if ![]() and
and ![]() , then
, then ![]() . A preferential theory
. A preferential theory ![]() that is closed under RM is called rational.
that is closed under RM is called rational.
Example 47 (Example 46 cont.). In our example we have: ![]() and
and ![]() , but
, but ![]() . So,
. So, ![]() does not validate RM, although it is preferential.
does not validate RM, although it is preferential.
As Example 47 shows, preferential models ![]() do not, in general, give rise to rational theories
do not, in general, give rise to rational theories ![]() . What kind of models are such that their induced conditional theories are rational? The key will be to let all states be comparable.
. What kind of models are such that their induced conditional theories are rational? The key will be to let all states be comparable.
Preferential models allow for incomparabilities of states in the following sense: there are ![]() for which
for which ![]() but
but ![]() is not comparable to
is not comparable to ![]() and
and ![]() . We have such a situation in Example 46. We notice that this is responsible for a violation of RM by
. We have such a situation in Example 46. We notice that this is responsible for a violation of RM by ![]() .
.
The RM property holds if the set of minimal states of ![]() is contained in the set of minimal states of
is contained in the set of minimal states of ![]() , in case there are some minimal states of
, in case there are some minimal states of ![]() that validate
that validate ![]() . In view of
. In view of ![]() , one may expect them to be, since there are indeed minimal states of
, one may expect them to be, since there are indeed minimal states of ![]() that do not satisfy
that do not satisfy ![]() and in which therefore
and in which therefore ![]() holds. In our example the outlier is
holds. In our example the outlier is ![]() . The situation improves if
. The situation improves if ![]() is comparable to
is comparable to ![]() and/or to
and/or to ![]() . In the rightmost model of Fig. 28 we have
. In the rightmost model of Fig. 28 we have ![]() ,
, ![]() , and
, and ![]() (while in the model in the center we have
(while in the model in the center we have ![]() ).
).

Figure 28 (Left) The preferential model ![]() of Example 46. (Middle and Right) Ranked models
of Example 46. (Middle and Right) Ranked models ![]() based on modular extension
based on modular extension ![]() of
of ![]() . The dashed arrow is optional.
. The dashed arrow is optional.
A ranked model ![]() is a preferential model for which
is a preferential model for which ![]() is modular, that is, for all
is modular, that is, for all ![]() , if
, if ![]() , then
, then ![]() or
or ![]() . It can easily be seen that an order is modular in case its states can be “ranked” by a function
. It can easily be seen that an order is modular in case its states can be “ranked” by a function ![]() to a total order
to a total order ![]() in such a way that
in such a way that ![]() iff
iff ![]() . So, any states
. So, any states ![]() and
and ![]() in a ranked model are comparable in that
in a ranked model are comparable in that ![]() or
or ![]() . Ranked models provide an adequate semantic characterization of rational theories.
. Ranked models provide an adequate semantic characterization of rational theories.
Theorem 13.3 (Lehmann and Magidor (1992)). (i) If ![]() is a ranked model,
is a ranked model, ![]() is a rational theory. (ii) If
is a rational theory. (ii) If ![]() is a rational theory, there is a ranked model
is a rational theory, there is a ranked model ![]() for which
for which ![]() .
.
13.3 What Does a Conditional Knowledge Base Entail?
While so far our focus has been on semantic characterizations of defaults, we now turn to a different, although related question. Given a set of defaults ![]() (of the form
(of the form ![]() ): what other defaults follow from them? To answer this question, one may take the principles LLE, RW, REF, OR, CM, and CT (and RM) underlying preferential (resp. rational) consequence relations and use them as metarules
): what other defaults follow from them? To answer this question, one may take the principles LLE, RW, REF, OR, CM, and CT (and RM) underlying preferential (resp. rational) consequence relations and use them as metarules ![]() , just like we have seen metarules being applied to defeasible rules in the context of input–output logic (see Section 11.3.2).
, just like we have seen metarules being applied to defeasible rules in the context of input–output logic (see Section 11.3.2).
The set of metarules consisting of LLE, RW, REF, OR, CM and CT is often referred to as system ![]() , while adding RM to
, while adding RM to ![]() results in system
results in system ![]() . Where
. Where ![]() , we write
, we write ![]() if
if ![]() is derivable from
is derivable from ![]() by means of the metarules in
by means of the metarules in ![]() .
.
Example 48. Suppose we have the set of defaults ![]() ;
; ![]() . Then,
. Then, ![]() follows from
follows from ![]() in both system
in both system ![]() and system
and system ![]() (by means of CM).
(by means of CM).
Given the representational results Theorems 13.1 to 13.3 from Section 13.1, 13.2 concerning the adequacy of preferential resp. of ranked models, it is easy to see that ![]() - and
- and ![]() -entailment can be semantically expressed. We say that a preferential model
-entailment can be semantically expressed. We say that a preferential model ![]() is a model of
is a model of ![]() iff for all
iff for all ![]() ,
, ![]() .
.
Theorem 13.4 (Lehmann and Magidor, 1992). Where ![]() is a set of defaults,
is a set of defaults, ![]() iff for all preferential models
iff for all preferential models ![]() of
of ![]() ,
, ![]() .
.
The preferential theory ![]() is called the preferential closure of
is called the preferential closure of ![]() . It is interesting, and maybe somewhat disappointing, to observe that for any
. It is interesting, and maybe somewhat disappointing, to observe that for any ![]() ,
, ![]() -entailment and
-entailment and ![]() -entailment are identical, that is,
-entailment are identical, that is, ![]() . This is for a rather trivial reason: the rule RM is also applied to negated defaults, no set of defaults
. This is for a rather trivial reason: the rule RM is also applied to negated defaults, no set of defaults ![]() contains such objects, and so RM is never applied. In fact, the question is, what is a more rewarding interpretation of
contains such objects, and so RM is never applied. In fact, the question is, what is a more rewarding interpretation of ![]() in the context of RM? It seems reasonable to consider RM as a closure principle, that is, a principle that extends
in the context of RM? It seems reasonable to consider RM as a closure principle, that is, a principle that extends ![]() to a set
to a set ![]() for which:
for which:
(†) if
(α1)
 and
and(α2)
 ,
,
(γ) then
 .
.
But, how to find such a set ![]() ? A first idea could be to simply take the theory provided by the intersection of the theories induced by ranked models of
? A first idea could be to simply take the theory provided by the intersection of the theories induced by ranked models of ![]() . But, as the following example shows, this does not work.
. But, as the following example shows, this does not work.
Example 49 (Example 48 cont.). We now show that, although
(α1) in all ranked models of
 ,
,  holds; and
holds; and(α2) there are ranked models of
 in which
in which  doesn’t hold; but
doesn’t hold; but(γ‾) there are ranked models of
 in which
in which  doesn’t hold.
doesn’t hold.
Given ![]() , in view of
, in view of ![]() , being a drummer is irrelevant to the question whether environmentalists are usually vegans (
, being a drummer is irrelevant to the question whether environmentalists are usually vegans (![]() ). If Anne is an environmentalist who happens to be a drummer, this should still allow us to infer that she (likely) is a vegan (
). If Anne is an environmentalist who happens to be a drummer, this should still allow us to infer that she (likely) is a vegan (![]() ). While from an intuitive point of view the rule RM seems to exactly allow for the strengthening of an antecedent with information that is not atypical for the antecedent (like being a drummer for being an environmentalist), the example demonstrates that it doesn’t fulfill this role. For this we consider the following states (where
). While from an intuitive point of view the rule RM seems to exactly allow for the strengthening of an antecedent with information that is not atypical for the antecedent (like being a drummer for being an environmentalist), the example demonstrates that it doesn’t fulfill this role. For this we consider the following states (where ![]() and in the case of
and in the case of ![]() we let
we let ![]() ):
):

Table 09Long description
The table consists of four columns: S subscript 1; S subscript 2; S subscript 3 superscript i, j, k, and S subscript 4 superscript i, j, k. It read as follows: Row 1: environmentalist: 1; 1; 1; 0. Row 2: vegan: 1; 1; i; i. Row 3: drummer: 0; 1; j; j. Row 4: avoidsFlying: 1; 1; k; k.
Figure 29 shows two ranked models of ![]() . Only
. Only ![]() validates
validates ![]() . Not so
. Not so ![]() , since
, since

The problem with ![]() is that it validates
is that it validates ![]() due to the fact that
due to the fact that

and in ![]() ,
, ![]() is true. In contrast, in
is true. In contrast, in ![]() ,
,

and since in ![]()
![]() holds,
holds, ![]() is invalid in this model, and by means of RM it has to be the case that
is invalid in this model, and by means of RM it has to be the case that ![]() holds. Indeed, in
holds. Indeed, in ![]() we have:
we have:

In sum, although each ranked model ![]() satisfies RM for its induced theory
satisfies RM for its induced theory ![]() , RM as interpreted in
, RM as interpreted in ![]() is not satisfied for the consequence relation induced by the ranked models. We need another approach.
is not satisfied for the consequence relation induced by the ranked models. We need another approach.
In order to let RM fulfill this role, it would seem that we need to interpret sentences ![]() as not being default entailed by
as not being default entailed by ![]() (i.e.,
(i.e., ![]() ) as much as possible, in order to allow for the inference from
) as much as possible, in order to allow for the inference from ![]() to
to ![]() via RM. After all, in all ranked models
via RM. After all, in all ranked models ![]() of
of ![]() in which
in which ![]() doesn’t hold,
doesn’t hold, ![]() holds (unlike in our
holds (unlike in our ![]() ). So, our strategy is to somehow trade in the invalidity of more general defaults (
). So, our strategy is to somehow trade in the invalidity of more general defaults (![]() ) for the validity of more specific defaults (
) for the validity of more specific defaults (![]() ). How to execute this tricky task?
). How to execute this tricky task?

Figure 29 Two ranked models of Example 49.
Figure 29 gives a hint at a procedure for this: when moving from model ![]() to
to ![]() we ranked one state, namely
we ranked one state, namely ![]() , more normal. We can generalize this: our goal is to rank each state as normal as possible. This intuitive idea can be made precise in terms of imposing an order
, more normal. We can generalize this: our goal is to rank each state as normal as possible. This intuitive idea can be made precise in terms of imposing an order ![]() on the ranked models of a given set of defaults
on the ranked models of a given set of defaults ![]() and to select the best model. The way two ranked models
and to select the best model. The way two ranked models ![]() and
and ![]() of
of ![]() are compared has an argumentative interpretation. Suppose there are two discussants, one arguing in favor of
are compared has an argumentative interpretation. Suppose there are two discussants, one arguing in favor of ![]() , the other one in favor of
, the other one in favor of ![]() . Each discussant produces attacks against the model favored by the other agent and defends her model against such attacks.
. Each discussant produces attacks against the model favored by the other agent and defends her model against such attacks. ![]() is preferred to
is preferred to ![]() (written:
(written: ![]() ) if the proponent of
) if the proponent of ![]() can attack
can attack ![]() such that the proponent of
such that the proponent of ![]() cannot defend
cannot defend ![]() , and
, and ![]() can be defended from every attack by the latter. But, how are attacks and defenses supposed to work?
can be defended from every attack by the latter. But, how are attacks and defenses supposed to work?
A proponent of ![]() may attack the model
may attack the model ![]() favored by the other agent by accusing it of validating too many inferential relations, that is, by pointing to a default
favored by the other agent by accusing it of validating too many inferential relations, that is, by pointing to a default ![]() that holds in
that holds in ![]() but not in
but not in ![]() . Recall that our goal is to invalidate for arbitrary
. Recall that our goal is to invalidate for arbitrary ![]() and
and ![]() the default
the default ![]() , if possible. There is a trade-off though, since invalidating some
, if possible. There is a trade-off though, since invalidating some ![]() may lead, via RM, to the strengthening of the antecedent of others, for example, from
may lead, via RM, to the strengthening of the antecedent of others, for example, from ![]() to
to ![]() .
.
In Fig. 29, the discussant arguing in favor of ![]() may attack the proponent of
may attack the proponent of ![]() by stating that
by stating that

However, a way to defend ![]() is to point out that (a)
is to point out that (a)

and (b) ![]() is according to
is according to ![]() ’s standards even more normal than
’s standards even more normal than ![]() (formally,
(formally, ![]() ).
).
Altogether, our informal discussion motivates the following definition of an order ![]() between models of a set of defaults
between models of a set of defaults ![]() . For this we let
. For this we let

Definition 13.1. Where ![]() and
and ![]() are two ranked models,
are two ranked models, ![]() iff the following two conditions hold:
iff the following two conditions hold:
- (defeat)
there is an
 such that
such that  , and
, and- (defense)
for all
 ,
,  .
.
(defeat) expresses that there is an attack from ![]() to
to ![]() which is undefendable, while (defense) expresses that every attack from
which is undefendable, while (defense) expresses that every attack from ![]() to
to ![]() can be defended. In terms of the preceding described argumentative reading, the two conditions describe winning conditions for the proponent of
can be defended. In terms of the preceding described argumentative reading, the two conditions describe winning conditions for the proponent of ![]() when arguing with an opponent favoring
when arguing with an opponent favoring ![]() .
.
Definition 13.2. In case there is a unique ![]() -minimal model
-minimal model ![]() among all ranked models of a given set of defaults
among all ranked models of a given set of defaults ![]() ,
, ![]() is called the rational closure of
is called the rational closure of ![]() .Footnote 54
.Footnote 54
Example 50 (Exaple 49 cont.). We consider models ![]() and
and ![]() in Fig. 29. We have
in Fig. 29. We have ![]() . (defeat) holds since
. (defeat) holds since

Also (defense) holds, for example, where ![]() , although
, although ![]() , there is
, there is

We now discuss an alternative characterization of the rational closure in terms of ranking sentences according to their normality (relative to ![]() ). This will also help defining a significant class of sets of defaults for which the rational closure exists, so-called admissible sets (see Proposition 13.1). For this we inductively associate sentences with ordinals via a function
). This will also help defining a significant class of sets of defaults for which the rational closure exists, so-called admissible sets (see Proposition 13.1). For this we inductively associate sentences with ordinals via a function ![]() . We say that a sentence
. We say that a sentence ![]() is exceptional for
is exceptional for ![]() in case
in case ![]() , so in case
, so in case ![]() expresses that normally
expresses that normally ![]() is false. Similarly,
is false. Similarly, ![]() is exceptional for
is exceptional for ![]() if
if ![]() is exceptional for
is exceptional for ![]() . We collect the exceptional defaults in
. We collect the exceptional defaults in ![]() in the set
in the set ![]() . Where
. Where ![]() , we let
, we let ![]() for all successor ordinals
for all successor ordinals ![]() and
and ![]() for all limit ordinals
for all limit ordinals ![]() . Now, some sentence
. Now, some sentence ![]() has a rank for
has a rank for ![]() in case there is a least ordinal
in case there is a least ordinal ![]() for which
for which ![]() is not exceptional for
is not exceptional for ![]() , in which case the rank of
, in which case the rank of ![]() is
is ![]() . Otherwise,
. Otherwise, ![]() has no rank.Footnote 55
has no rank.Footnote 55
Example 51 (Example 50 cont.). For all ![]() ,
, ![]() and
and ![]() are not exceptional for
are not exceptional for ![]() and so have rank 0. Exceptional for
and so have rank 0. Exceptional for ![]() are, for instance,
are, for instance, ![]() and
and ![]() . These formulas have rank 1.
. These formulas have rank 1.
We call a set ![]() admissible if for every sentence
admissible if for every sentence ![]() that has no rank,
that has no rank, ![]() . Examples for admissible sets are sets
. Examples for admissible sets are sets ![]() based on a finite language (a language with only finitely many atoms), or for which the preferential closure has no infinite sequences of more and more normal sentences.
based on a finite language (a language with only finitely many atoms), or for which the preferential closure has no infinite sequences of more and more normal sentences.
Proposition 13.1 (Lehmann and Magidor (1990). Where ![]() is admissible, the rational closure of
is admissible, the rational closure of ![]() exists and it consists of all
exists and it consists of all ![]() for which
for which ![]() has no rank, or for which
has no rank, or for which ![]() .
.
Example 52 (Example 51 cont.). In view of Proposition 13.1, for instance, ![]() is in the rational closure of
is in the rational closure of ![]() since
since ![]() has rank 0 while
has rank 0 while ![]() has rank 1.
has rank 1.
However, ![]() is not in the rational closure of
is not in the rational closure of ![]() since
since

have the same rank, namely 1. This shows that rational closure “suffers” from the drowning problem (see Section 1.2): since nonvegans are exceptional with respect to ![]() , they turn out exceptional also with respect to
, they turn out exceptional also with respect to ![]() .Footnote 56
.Footnote 56
14 Quantitative Methods
So far, we have interpreted ![]() as
as ![]() holds in the most normal situations in which
holds in the most normal situations in which ![]() holds (recall (⋆)). According to a similar idea:
holds (recall (⋆)). According to a similar idea:
- (
 )
)  holds if, given
holds if, given  ,
,  is more normal/plausible/etc. than
is more normal/plausible/etc. than  .
.
The notion of normality was rendered precise in terms of a preference order on the logically possible situations. Instead of this qualitative approach, one may follow the idea behind ![]() but proceed quantitatively and interpret
but proceed quantitatively and interpret ![]() in terms of probabilities: given
in terms of probabilities: given ![]() ,
, ![]() is more probable than
is more probable than ![]() . In what follows we introduce the central approach to probabilistic semantics by Adams (Reference Adams1975), which corresponds to system
. In what follows we introduce the central approach to probabilistic semantics by Adams (Reference Adams1975), which corresponds to system ![]() .Footnote 57
.Footnote 57
14.1 Adams’ Approach:  -Semantics
-Semantics
We again consider a set of situations ![]() interpreted via an assignment
interpreted via an assignment ![]() .Footnote 58
.Footnote 58
We now equip ![]() with a probability function
with a probability function ![]() which maps sets of situations into
which maps sets of situations into ![]() such that (1)
such that (1) ![]() and (2) for any pairwise disjoint
and (2) for any pairwise disjoint ![]() ,
, ![]() . We call each
. We call each ![]() a probabilistic model. For every formula
a probabilistic model. For every formula ![]() , a probabilistic model provides information of how probable it is to be in a situation consistent with
, a probabilistic model provides information of how probable it is to be in a situation consistent with ![]() . Where
. Where ![]() (we skip the subscript when the context disambiguates), we will write
(we skip the subscript when the context disambiguates), we will write ![]() instead of
instead of ![]() for the formal expression of this information. The conditional probability
for the formal expression of this information. The conditional probability ![]() is, as usual, defined by
is, as usual, defined by ![]() in case
in case ![]() (otherwise, it is undefined). It expresses the probability of being in a situation in which
(otherwise, it is undefined). It expresses the probability of being in a situation in which ![]() holds, given that
holds, given that ![]() holds.
holds.
Example 53. Let ![]() , where
, where ![]() stands for ‘being a bird’,
stands for ‘being a bird’, ![]() for ‘flying’ and
for ‘flying’ and ![]() for ‘having wings’. The probabilistic models
for ‘having wings’. The probabilistic models ![]() and
and ![]() are given by Table 11.
are given by Table 11.
We have, for instance, ![]() ,
, ![]() and therefore
and therefore ![]() , while
, while ![]() ,
, ![]() and
and ![]() .
.

Table 11Long description
The table consists of six columns: situations; s Double Turnstile b; s Double Turnstile f; s Double Turnstile w; p subscript 1; and p subscript 2. It read as follows: Row 1: s subscript 1; checkmark; Blank; Blank; dot 2; dot 1. Row 2: s subscript 2; checkmark; Blank; checkmark; dot 2; dot 1. Row 3: s subscript 3; checkmark; checkmark; Blank; dot 2; dot 2. Row 4: s subscript 4; checkmark; checkmark; checkmark; dot 4; dot 2. Row 5: s subscript 1 prime; Blank; Blank; Blank; 0; dot 1. Row 6: s subscript 2 prime; Blank; Blank; checkmark; 0; dot 1. Row 7: s subscript 3 prime; Blank; checkmark; Blank; 0; dot 1. Row 8: s subscript 4 prime; Blank; checkmark; checkmark; 0; dot 1.
We now define when a default ![]() holds in a given probabilistic model
holds in a given probabilistic model ![]() (in signs,
(in signs, ![]() ). A consequence relation can then be defined as follows. Where
). A consequence relation can then be defined as follows. Where ![]() is a set of defaults:
is a set of defaults: ![]() iff for all probabilistic models
iff for all probabilistic models ![]() of
of ![]() ,
, ![]() .Footnote 59 Before moving to Adams’ approach, we state three naive ideas. Let
.Footnote 59 Before moving to Adams’ approach, we state three naive ideas. Let ![]() .
.
Naive 1
 , iff
, iff  or if
or if  .Footnote 60
.Footnote 60Naive 2
 , iff
, iff  or if
or if  .
.Naive 3
 , iff
, iff  for some threshold value
for some threshold value  (such as
(such as  ), or if
), or if  .Footnote 61
.Footnote 61
We note that approaches Naive 1 and Naive 2 are equivalent since, in case ![]() :
: ![]() , iff
, iff ![]() , iff
, iff ![]() . The weakness of the preceding naive approaches can be illustrated by applying them to our example.
. The weakness of the preceding naive approaches can be illustrated by applying them to our example.
Example 54 (Example 53 cont.). Let ![]() . In model
. In model ![]() we have
we have ![]() which is why
which is why ![]() . Similarly,
. Similarly, ![]() , which is why
, which is why ![]() . However, since
. However, since ![]() , we also have
, we also have ![]() , even
, even ![]() .
.
This means that AND is violated for the induced consequence relation. This model allows for a situation where ![]() , albeit
, albeit ![]() is an inconsistent set. Similarly, other central properties of nonmonotonic entailment, such as CT, fail in our naive approaches.
is an inconsistent set. Similarly, other central properties of nonmonotonic entailment, such as CT, fail in our naive approaches.
In view of these weaknesses, Adams introduced another approach. In his semantics the degree of assertability of ![]() is modelled by the conditional probability
is modelled by the conditional probability ![]() . In a nutshell, the central idea is that some
. In a nutshell, the central idea is that some ![]() is entailed by a set of defaults
is entailed by a set of defaults ![]() in case its assertability approximates 1 when the elements of
in case its assertability approximates 1 when the elements of ![]() are being interpreted as increasingly assertable. In formal terms, let
are being interpreted as increasingly assertable. In formal terms, let ![]() be a proper probability function for
be a proper probability function for ![]() in case
in case ![]() for all
for all ![]() . We define:
. We define:
Definition 14.1 (ϵ-entailment, Adams, 1975; Pearl, 1989). Let ![]() be a set of defaults. We define:
be a set of defaults. We define: ![]() , iff, for any
, iff, for any ![]() , there is a
, there is a ![]() such that for all proper probability functions
such that for all proper probability functions ![]() for
for ![]() : if, for all
: if, for all ![]() ,
, ![]() , then
, then ![]() .
.
Does this approach lead to a more well-behaved entailment relation and what are characteristic properties of ![]() -entailment? Let us have another look at our example.
-entailment? Let us have another look at our example.
Example 55 (Example 54 cont.). Where ![]() , we have, for instance,
, we have, for instance, ![]() . In order to show this, let
. In order to show this, let ![]() be arbitrary and consider a probability function
be arbitrary and consider a probability function ![]() . We need to find a
. We need to find a ![]() such that if
such that if ![]() , then
, then ![]() . Let
. Let ![]() and suppose that
and suppose that ![]() . Then,
. Then,

What we have just shown in the context of our example is not coincidental. Indeed, the proof of AND for ![]() -entailment follows exactly the structure of the proof in Example 55. What is more,
-entailment follows exactly the structure of the proof in Example 55. What is more, ![]() -entailment can be shown to coincide with system
-entailment can be shown to coincide with system ![]() for finite knowledge bases (Geffner, Reference Geffner1992; Lehmann & Magidor, Reference Lehmann and Magidor1990): a remarkable correspondence between two rather different perspectives on the meaning of
for finite knowledge bases (Geffner, Reference Geffner1992; Lehmann & Magidor, Reference Lehmann and Magidor1990): a remarkable correspondence between two rather different perspectives on the meaning of ![]() .
.
14.2 Other Quantitative Approaches
We close this section with some pointers to related approaches. While in Adams’ approach we find a probabilistic characterization of ![]() -entailment, the reader may wonder whether also
-entailment, the reader may wonder whether also ![]() -entailment can be represented by a quantitative approach. Indeed, utilizing a nonstandard probabilistic approach including infinitesimal values, Lehmann and Magidor (Reference Lehmann and Magidor1992) present a variant of Adams’ system that characterizes rational entailment.
-entailment can be represented by a quantitative approach. Indeed, utilizing a nonstandard probabilistic approach including infinitesimal values, Lehmann and Magidor (Reference Lehmann and Magidor1992) present a variant of Adams’ system that characterizes rational entailment.
Instead of probability measures other quantitative measures have been utilized in the literature to give meaning to defaults. We let ![]() again be a finite set of situations and
again be a finite set of situations and ![]() an assignment function.
an assignment function.
A possibility measure (Dubois & Prade, Reference Dubois, Prade, Shafer and Pearl1990)
 determines the possibility of a set of situations, from impossible (0) to maximally possible (1).Footnote 62 It is required that
determines the possibility of a set of situations, from impossible (0) to maximally possible (1).Footnote 62 It is required that  ,
,  , and for any
, and for any  ,
,  . A possibilistic model
. A possibilistic model  is of the form
is of the form  .
.An ordinal ranking function (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1992; Spohn, Reference Spohn, Harper and Skyrms1988)
 associates each set of situations with a level of surprise, from unsurprising (0) to shocking (
associates each set of situations with a level of surprise, from unsurprising (0) to shocking ( ). It is required that
). It is required that  ,
,  , and, for any
, and, for any  ,
,  . An ordinal ranking model
. An ordinal ranking model  is of the form
is of the form  .
.
It is easy to see that letting ![]() iff
iff ![]() in the context of a possibilistic model
in the context of a possibilistic model ![]() [resp. iff
[resp. iff ![]() in the context of an ordinal ranking model
in the context of an ordinal ranking model ![]() ] gives rise to a ranked model
] gives rise to a ranked model ![]() .
.
In each of these approaches the meaning of defaults in a given model is defined analogous to the underlying idea of (![]() ):
):
Where
 is a possibilistic model, we let
is a possibilistic model, we let  iff
iff  or
or 
Where
 is an ordinal ranking model, we let
is an ordinal ranking model, we let  iff
iff  or
or  .
.
We say that a possibilistic model [resp. an ordinal ranking model] ![]() is a model of a set of defaults
is a model of a set of defaults ![]() in case
in case ![]() for all
for all ![]() .
.
For instance, a possibilistic model verifies ![]() just in case
just in case ![]() is impossible, or if
is impossible, or if ![]() is strictly more possible than
is strictly more possible than ![]() . Since ranking functions model the level of surprise an agent would face when learning that some
. Since ranking functions model the level of surprise an agent would face when learning that some ![]() is true, according to a ranking function
is true, according to a ranking function ![]() is valid in case
is valid in case ![]() would cause maximal surprise or if learning about
would cause maximal surprise or if learning about ![]() would cause strictly less surprise than learning about
would cause strictly less surprise than learning about ![]() .
.
Example 56 (Ex. 53 cont.). We consider the set of states ![]() in Example 53. Fig. 30 shows a cardinal ranking function
in Example 53. Fig. 30 shows a cardinal ranking function ![]() and a possibility function
and a possibility function ![]() . Recall that for
. Recall that for ![]() ,
,

which is why the figure fully characterizes ![]() and
and ![]() by illustrating what values are assigned to single states. Where
by illustrating what values are assigned to single states. Where ![]() and
and ![]() , we have:
, we have:
 since
since 
 since
since 
 since
since  , and
, and since
since  .
.

Figure 30 Example 56. (Left) The cardinal ranking ![]() . (Right) The possibility function
. (Right) The possibility function ![]() .
.
Entailment relations are induced in the usual way. Given a set of defaults ![]() , we let
, we let
 iff for all possibilistic models
iff for all possibilistic models  of
of  ,
,  ,
, iff for all ordinal ranking models
iff for all ordinal ranking models  of
of  ,
,  .
.
It is a most astonishing result in NML that all these different perspectives lead exactly to a characterization of ![]() -entailment, a result that strongly underlines the central character of its underlying reasoning principles.
-entailment, a result that strongly underlines the central character of its underlying reasoning principles.
Theorem 14.1 (Dubois and Prade, 1991; Geffner, 1992; Lehmann and Magidor, 1992). Let ![]() be a finite set of defaults. We have:
be a finite set of defaults. We have: ![]() iff
iff ![]() iff
iff ![]() iff
iff ![]() iff
iff ![]() .
.
15 A Preferential Semantics for Some NMLs
In this section we present a preferential semantics for logics based on temperate accumulation and knowledge bases of the type ![]() ,Footnote 63 such as Rescher and Manor’s logics based on maxicon sets and Makinson’s default assumptions (see Section 11.3.1).
,Footnote 63 such as Rescher and Manor’s logics based on maxicon sets and Makinson’s default assumptions (see Section 11.3.1).
In fact, this is exactly the semantics we introduced in Section 5.3, so our main aim in this section is to show its adequacy for temperate accumulation. We refer to Example 21, 22 in Section 5.3 for an illustration of this idea.
Let us briefly recall the general setup. We work in the context of a Tarski logic ![]() (such as classical logic) which has an adequate model-theoretic semantic representation: for any set of
(such as classical logic) which has an adequate model-theoretic semantic representation: for any set of ![]() -sentences
-sentences ![]() it holds:
it holds: ![]() iff for all
iff for all ![]() -models
-models ![]() of
of ![]() (i.e., for all
(i.e., for all ![]() ,
, ![]() ) it is the case that
) it is the case that ![]() . In particular, we assume that the consistency of a set of sentences
. In particular, we assume that the consistency of a set of sentences ![]() can be expressed by
can be expressed by ![]() .
.
In order to determine whether ![]() defeasibly follows from
defeasibly follows from ![]() , we compare the
, we compare the ![]() -models of the strict assumptions
-models of the strict assumptions ![]() in terms of how normal they interpret the defeasible assumptions in
in terms of how normal they interpret the defeasible assumptions in ![]() . For this, we consider the normal part of a given model
. For this, we consider the normal part of a given model ![]() , which is simply the subset of defeasible assumptions it validates:
, which is simply the subset of defeasible assumptions it validates: ![]() . Now we define an order on the
. Now we define an order on the ![]() -models of
-models of ![]() by:
by:

We select the most normal models of ![]() and define a consequence relation
and define a consequence relation ![]() by:
by:

In the following we show how ![]() and
and ![]() can be characterized by a semantics based on
can be characterized by a semantics based on ![]() .Footnote 64 For this we make use of the characterization of temperate accumulation in terms of maxicon sets (see Lemma 10.1 and Theorem 10.1).
.Footnote 64 For this we make use of the characterization of temperate accumulation in terms of maxicon sets (see Lemma 10.1 and Theorem 10.1).
Theorem 15.1. Let ![]() be a knowledge base. Then,
be a knowledge base. Then, ![]() iff
iff ![]() .
.
The theorem follows in view of the following lemmas.
Lemma 15.1. For every ![]() ,
, ![]() .
.
Proof. Suppose that ![]() and let
and let ![]() . Thus,
. Thus, ![]() is consistent. Consider some
is consistent. Consider some ![]() for which
for which ![]() is consistent and
is consistent and ![]() . Thus, there is a
. Thus, there is a ![]() . Since
. Since ![]() ,
, ![]() and by the
and by the ![]() -minimality of
-minimality of ![]() ,
, ![]() . Thus,
. Thus, ![]() . □
. □
Lemma 15.2. For every ![]() there is an
there is an ![]() for which
for which ![]() .
.
Proof. Suppose ![]() . By the consistency of
. By the consistency of ![]() , there is an
, there is an ![]() . Consider a
. Consider a ![]() for which
for which ![]() . Then
. Then ![]() is consistent. Since
is consistent. Since ![]() and the maximality of
and the maximality of ![]() ,
, ![]() . So,
. So, ![]() and thus,
and thus, ![]() . □
. □
Proof of Theorem 15.1 ![]() , iff [by Proposition 11.3], for all
, iff [by Proposition 11.3], for all ![]() ,
, ![]() , iff [by Lemmas 15.1 and 15.2], for all
, iff [by Lemmas 15.1 and 15.2], for all ![]() ,
, ![]() , iff,
, iff, ![]() . □
. □
We now move on to characterize ![]() semantically. We can capture this consequence relation by defining a threshold function
semantically. We can capture this consequence relation by defining a threshold function ![]() on the degree of normality a selected model is allowed to have.
on the degree of normality a selected model is allowed to have.

So the core of ![]() consists of those models whose normal part contains at least all those sentences that are part of the normal parts of every
consists of those models whose normal part contains at least all those sentences that are part of the normal parts of every ![]() -minimal model. Clearly, each
-minimal model. Clearly, each ![]() -minimal model belongs to the core, but possibly also other models. Let, moreover,
-minimal model belongs to the core, but possibly also other models. Let, moreover,

Given that ![]() , the consequence relation
, the consequence relation ![]() will typically give rise to a more cautious reasoning style than
will typically give rise to a more cautious reasoning style than ![]() .
.
Example 57 (Example 21 cont.). For our ![]() with
with

and ![]() we have three minimal models:
we have three minimal models: ![]() with
with ![]() ,
, ![]() with
with ![]() , and
, and ![]() with
with ![]() (see Fig. 12). So,
(see Fig. 12). So, ![]() and therefore
and therefore ![]() , and
, and ![]() iff
iff ![]() . This highlights the fact that
. This highlights the fact that ![]() leads to a more cautious reasoning style than
leads to a more cautious reasoning style than ![]() .
.
We now consider ![]() , where
, where ![]() . In Fig. 31 we highlight the models in
. In Fig. 31 we highlight the models in ![]() . In this case
. In this case ![]() . This is reflected, for instance, in the consequences
. This is reflected, for instance, in the consequences ![]() while
while ![]() , and
, and ![]() while
while ![]() .
.

Figure 31 The order ![]() on the models of
on the models of ![]() in Example 57. Highlighted are the models in
in Example 57. Highlighted are the models in ![]() . The atoms
. The atoms ![]() , and
, and ![]() are true in every model of
are true in every model of ![]() .
.
With Lemmas 15.1 and 15.2 we immediately get:
Corollary 15.1. Let ![]() be a knowledge base and
be a knowledge base and ![]() . Then,
. Then, ![]() iff
iff ![]() .
.
Theorem 15.2. Let ![]() be a knowledge base. Then,
be a knowledge base. Then, ![]() iff
iff ![]() .
.
Proof. Suppose ![]() . Thus, by Proposition 11.3,
. Thus, by Proposition 11.3, ![]() . Let
. Let ![]() . By Corollary 15.1,
. By Corollary 15.1, ![]() and so
and so ![]() . Thus,
. Thus, ![]() . So,
. So, ![]() .
.
Suppose ![]() . Thus, by Proposition 11.3,
. Thus, by Proposition 11.3, ![]() . So, there is a
. So, there is a ![]() such that
such that ![]() . So,
. So, ![]() . By Corollary 15.1,
. By Corollary 15.1, ![]() . So,
. So, ![]() . □
. □
Combining our previous results with the result in Proposition 11.3, we get:
Corollary 15.2. Let ![]() be a knowledge base. Then,
be a knowledge base. Then,
1.
 iff
iff  iff
iff  .
.2.
 iff
iff  iff
iff  .
.
16 Logic Programming
Logic programming is a declarative approach to problem solving. The idea is that a user describes a given reasoning problem by means of a so-called logic program in a simple syntax, without the need of encoding an algorithm to solve the problem. Automated proof procedures or semantic methods are then used to provide answers to queries. With the addition of negation-as-failure(-to-prove) (Section 16.1) or default negation, logic programming became a key paradigm in NML. It gave rise to a rich variety of applications, from legal reasoning (Sergot et al., Reference Sergot, Sadri, Kowalski, Kriwaczek, Hammond and Cory1986), to planning (including applications for the Space Shuttle program in Nogueira et al. (Reference Nogueira, Balduccini, Gelfond, Watson and Barry2001)), to cognitive science (Stenning & Van Lambalgen, Reference Stenning and Van Lambalgen2008), and others. In this section we will introduce one of the central semantical approaches based on stable models (Section 16.2), which under the addition of classical negation became known as answer set programming (in short: ASP, Section 16.3). In Section 16.4 we note that ASP and default logic coincide under a translation and that ASP can be considered a form of formal argumentation.
16.1 Normal Logic Programs and Default Negation
A logic program in its simplest form is a collection of strict inference rules of the form
 (16.1.1)
(16.1.1)
where ![]() are atomic formulas (incl.
are atomic formulas (incl. ![]() or
or ![]() ).Footnote 65 These rules are called the clauses of the program. Factual information is represented by rules with empty bodies, such as
).Footnote 65 These rules are called the clauses of the program. Factual information is represented by rules with empty bodies, such as ![]() . We reason with such programs as one would expect:
. We reason with such programs as one would expect: ![]() follows from a program
follows from a program ![]() just in case there is an argument based on
just in case there is an argument based on ![]() with the conclusion
with the conclusion ![]() (recall Definition 5.1).
(recall Definition 5.1).
Similar to default logic, logic programming also accommodates defeasible assumptions in the body of rules such as:
On Sunday mornings Jane goes jogging, except it is stormy.
In logic programming the “except …” part is expressed with a dedicated negation ![]() whose exact interpretation we discuss as follows:
whose exact interpretation we discuss as follows:
 (16.1.2)
(16.1.2)
More generally, we are now dealing with rules of the form
 (16.1.3)
(16.1.3)
where ![]() are atomic formulas. Sets of rules
are atomic formulas. Sets of rules ![]() of the form (16.1.3) are called normal logic programs. The technical term for
of the form (16.1.3) are called normal logic programs. The technical term for ![]() is “negation-as-failure(-to-prove)” or simply “default negation.” The basic idea is that
is “negation-as-failure(-to-prove)” or simply “default negation.” The basic idea is that ![]() is considered true in the context of
is considered true in the context of ![]() unless there is an argument for
unless there is an argument for ![]() (based on
(based on ![]() ). So,
). So, ![]() is entailed by the program only consisting of the rule (16.1.2), but if we add
is entailed by the program only consisting of the rule (16.1.2), but if we add ![]() it should not be entailed.
it should not be entailed.
How to define a nonmonotonic consequence relation for negation-as-failure? Prima facie, the following simple (but ultimately flawed) idea seems to be in its spirit. We consider arguments that can be built with the rules in the given program ![]() and that are based on defeasible assumptions of the type
and that are based on defeasible assumptions of the type ![]() . Let for this
. Let for this ![]() be all formulas of the type
be all formulas of the type ![]() , where
, where ![]() occurs in some rule in
occurs in some rule in ![]() and let
and let ![]() be the knowledge base consisting of the defeasible assumptions
be the knowledge base consisting of the defeasible assumptions ![]() and the strict rules in
and the strict rules in ![]() . So
. So ![]() is of the form
is of the form ![]() , or in shorter notation
, or in shorter notation ![]() . We then let an atom
. We then let an atom ![]() be entailed by
be entailed by ![]() just in case the following two criteria are fulfilled:
just in case the following two criteria are fulfilled:
1. there is an argument
 for
for  in
in  (recall Definition 5.1), and
(recall Definition 5.1), and2. there is no argument for
 in
in  for any
for any  occurring in
occurring in  .
.
This would allow us to conclude ![]() from
from

The reason is that, where ![]() , there is an argument
, there is an argument ![]() in
in ![]() for
for ![]() , namely
, namely ![]() , and there is no argument for
, and there is no argument for ![]() in
in ![]() . At the same time, this approach blocks the conclusion
. At the same time, this approach blocks the conclusion ![]() from
from ![]() since now there is an argument
since now there is an argument ![]() for
for ![]() in
in ![]() , where
, where ![]() .
.
However, we run quickly into problems with our naive approach once the logic programs are slightly more involved.
Example 58. Consider, for instance, the following logic program:

In this case, although it seems reasonable to infer ![]() , our naive approach doesn’t permit it. To see this, we observe that the argument
, our naive approach doesn’t permit it. To see this, we observe that the argument ![]() for
for ![]() relies on the assumption
relies on the assumption ![]() . Although
. Although ![]() can be concluded in view of a (counter-)argument
can be concluded in view of a (counter-)argument ![]() based on the assumption
based on the assumption ![]() , the latter is problematic since
, the latter is problematic since ![]() follows strictly in
follows strictly in ![]() by the argument
by the argument ![]() . This kind of reinstatement, in which an attacked argument is successfully defended by a nonattacked argument, cannot be handled by our naive approach.Footnote 66
. This kind of reinstatement, in which an attacked argument is successfully defended by a nonattacked argument, cannot be handled by our naive approach.Footnote 66
Several ways that deal with such and similar problems have been proposed in various semantics for logic programming (see e.g., Eiter et al. (Reference Eiter, Ianni and Krennwallner2009)). In the following we will focus paradigmatically on one of the central approaches based on so-called stable models (Gelfond & Lifschitz, Reference Gelfond and Lifschitz1988).
16.2 Stable Models
A way to tackle the problem of reasoning with logic programs that contain default negation is by considering interpretations of programs. Let us start with the simple case of a ![]() -free logic program
-free logic program ![]() consisting of rules of the form (16.1.1). A model
consisting of rules of the form (16.1.1). A model ![]() of
of ![]() is a function that associates each atom
is a function that associates each atom ![]() occurring in a rule in
occurring in a rule in ![]() with true (written
with true (written ![]() ) or false (written
) or false (written ![]() ). As usual, we let
). As usual, we let ![]() and
and ![]() . Where
. Where ![]() , we write
, we write ![]() (“
(“![]() validates
validates ![]() ”) in case
”) in case ![]() , …,
, …, ![]() implies
implies ![]() . A compact representation is by letting
. A compact representation is by letting ![]() be the set of those atoms in
be the set of those atoms in ![]() that it interprets as true (and so
that it interprets as true (and so ![]() iff
iff ![]() ).Footnote 67
).Footnote 67
Example 59. Let ![]() and consider
and consider ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then,
. Then, ![]() ,
, ![]() , and
, and ![]() are not models of
are not models of ![]() :
: ![]() and
and ![]() violate the first rule (since
violate the first rule (since ![]() and
and ![]() ) and
) and ![]() violates the second rule (since
violates the second rule (since ![]() although
although ![]() ). The only model of
). The only model of ![]() is
is ![]() .
.
It is easy to see that a ![]() -free program
-free program ![]() has a minimal model, that is, a model
has a minimal model, that is, a model ![]() of
of ![]() such that for all other models
such that for all other models ![]() of
of ![]() ,
, ![]() . In fact, as the reader can easily verify, the minimal program will consist exactly of the conclusions of arguments based on the rules in
. In fact, as the reader can easily verify, the minimal program will consist exactly of the conclusions of arguments based on the rules in ![]() .
.
Fact 16.1. Let ![]() be a
be a ![]() -free program. Then,
-free program. Then, ![]() is the minimal model of
is the minimal model of ![]() .
.
As we have seen in the previous section, things get more interesting when we also consider default negation ![]() . For this we adjust the notion of validity in a model.
. For this we adjust the notion of validity in a model.
Definition 16.1. Let ![]() be a set of atoms. We let
be a set of atoms. We let
 , iff,
, iff,  or
or  and
and , iff,
, iff,  .
.
Where ![]() is a rule of type (16.1.3),
is a rule of type (16.1.3),
 , iff,
, iff,  , …,
, …,  ,
,  , …,
, …,  implies
implies  .
.
We write ![]() for the set
for the set ![]() and
and ![]() for the set of atoms occurring in
for the set of atoms occurring in ![]() .
.
Let ![]() be a normal logic program and
be a normal logic program and ![]() . We say that
. We say that ![]() is a model of
is a model of ![]() in case
in case ![]() for all
for all ![]() . We write
. We write ![]() for the set of all models of
for the set of all models of ![]() .
.
By having another look at ![]() we note that not all models of a given program are equally representative of a rational reasoner.
we note that not all models of a given program are equally representative of a rational reasoner.
Example 60 (Example 58 cont.). We consider the following candidates for models of ![]() :
:

We have ![]() for
for ![]() and
and ![]() .
. ![]() is not a model of
is not a model of ![]() since
since ![]() .
. ![]() and
and ![]() are models of
are models of ![]() .
.
However, we also notice problems with ![]() . In particular we have
. In particular we have ![]() , although the only argument for
, although the only argument for ![]() based on
based on ![]() is
is ![]() while
while ![]() . So,
. So, ![]() is “unfounded” in
is “unfounded” in ![]() : it is valid but not supported by an argument in
: it is valid but not supported by an argument in ![]() . A desideratum for us will thus be that models
. A desideratum for us will thus be that models ![]() of a program
of a program ![]() are founded in these programs in the sense that every atom contained in
are founded in these programs in the sense that every atom contained in ![]() can be inferred by means of
can be inferred by means of ![]() and the defeasible assumptions
and the defeasible assumptions ![]() in
in ![]() . Let us make this precise.
. Let us make this precise.
Definition 16.2. Let ![]() be a normal logic program and
be a normal logic program and ![]() be a model. We let
be a model. We let ![]() be the knowledge base consisting of the defeasible assumptions in
be the knowledge base consisting of the defeasible assumptions in ![]() and the rules in
and the rules in ![]() . A model
. A model ![]() of
of ![]() is founded (in
is founded (in ![]() ) if for each
) if for each ![]() there is an argument
there is an argument ![]() with conclusion
with conclusion ![]() (so,
(so, ![]() ).
).
In order to filter out unfounded models, Gelfond and Lifschitz (Reference Gelfond and Lifschitz1988) have proposed the concept of a reduction program.
Definition 16.3. Given a model ![]() of
of ![]() , we let the reduction of
, we let the reduction of ![]() by
by ![]() , written
, written ![]() , be the result of (i) replacing each occurrence of a
, be the result of (i) replacing each occurrence of a ![]() -negated formula
-negated formula ![]() in
in ![]() by
by ![]() in case
in case ![]() and by
and by ![]() else, and of (ii) adding the rule
else, and of (ii) adding the rule ![]() .
.
Definition 16.4. Let ![]() be a normal logic program.
be a normal logic program. ![]() is a stable model of
is a stable model of ![]() in case it is identical to the minimal model of
in case it is identical to the minimal model of ![]() . We write
. We write ![]() for the set of stable models of
for the set of stable models of ![]() .
.
It is reassuring to note that (a) ![]() is a
is a ![]() -free program and therefore has a minimal model (see Fact 16.1), and (b) if
-free program and therefore has a minimal model (see Fact 16.1), and (b) if ![]() is a model of
is a model of ![]() , then it is also a model of
, then it is also a model of ![]() .
.
Lemma 16.1. Let ![]() and
and ![]() . Then,
. Then, ![]() .
.
Proof. Let ![]() such that
such that ![]() and
and ![]() for each
for each ![]() . Thus,
. Thus, ![]() . Since
. Since ![]() ,
, ![]() . □
. □
Example 61 (Example 60 cont.). Let us put this idea to a test with ![]() and the two models
and the two models ![]() and
and ![]() .
.

Table 010Long description
The table consists of three columns: pi constant subscript 2; pi constant subscript 2 superscript M subscript 1; and pi constant subscript 2 superscript M subscript 2. It read as follows: Row 1: not q right arrow r; Top right arrow r; Bottom right arrow r. Row 2: not s right arrow q; Bottom right arrow q; and Bottom right arrow q. Row 3: right arrow s; right arrow s; and right arrow s. Row 4: Blank; right arrow Top; and right arrow Top.
The minimal model of ![]() is
is ![]() , the minimal model of
, the minimal model of ![]() is
is ![]() . So, as expected, while
. So, as expected, while ![]() is a stable model of
is a stable model of ![]() ,
, ![]() is not.
is not.
Stable models do not exist for every program. Indeed, for some logic programs the only existing models are unfounded ones.
Example 62. A case in point is ![]() . Note that
. Note that ![]() is not a model of
is not a model of ![]() since
since ![]() and so
and so ![]() would have to be true in
would have to be true in ![]() to be a model of
to be a model of ![]() . So we are left with
. So we are left with ![]() . But this model is not founded.Footnote 68
. But this model is not founded.Footnote 68
Programs containing conflicts may give rise to several stable models.
Example 63. As a simple example, consider ![]() .
. ![]() is not a model of
is not a model of ![]() , since both rules are applicable in
, since both rules are applicable in ![]() , but
, but ![]() . On the other hand,
. On the other hand, ![]() is not minimal (and hence unfounded), since neither rule is applicable in
is not minimal (and hence unfounded), since neither rule is applicable in ![]() . We are left with
. We are left with ![]() and
and ![]() . As the reader can easily verify, these two models are stable.
. As the reader can easily verify, these two models are stable.
16.3 Extended Logic Programs and Answer Sets
So far we have limited our attention to a rather weak language, only consisting of atoms and their default negations. We now will add another negation ![]() to the mix which will behave more similar to classical negation. This puts us in the realm of extended logic programs, which are sets of rules of the form
to the mix which will behave more similar to classical negation. This puts us in the realm of extended logic programs, which are sets of rules of the form
 (16.3.1)
(16.3.1)
where ![]() are
are ![]() -literals, that is, atoms or
-literals, that is, atoms or ![]() -negated atoms.
-negated atoms. ![]() denotes the set of all
denotes the set of all ![]() -literals occurring in an extended program
-literals occurring in an extended program ![]() .
.
It is our task now to enhance the notion of a model to extended programs. A simple way is by means of a translation ![]() of a given extended program
of a given extended program ![]() to a normal program
to a normal program ![]() (Gelfond & Lifschitz, Reference Gelfond and Lifschitz1991) in which each occurrence of some
(Gelfond & Lifschitz, Reference Gelfond and Lifschitz1991) in which each occurrence of some ![]() is replaced by a new atom
is replaced by a new atom ![]() (not occurring in
(not occurring in ![]() ). We then consider only those models
). We then consider only those models ![]() of
of ![]() for which
for which
 or
or  for all atoms
for all atoms  or
or contains all
contains all  and
and  for all atoms
for all atoms  in
in  .Footnote 69
.Footnote 69
We then translate ![]() back by considering
back by considering ![]() , replacing atoms of the form
, replacing atoms of the form ![]() by
by ![]() . If
. If ![]() is a stable model of
is a stable model of ![]() then we define
then we define ![]() to be a stable model of
to be a stable model of ![]() . The latter are also known as answer sets of
. The latter are also known as answer sets of ![]() .
.
Of course, we can also define a nonmonotonic consequence relation based on answer sets: where ![]() is a
is a ![]() -literal, or a
-literal, or a ![]() -negated
-negated ![]() -literal and
-literal and ![]() is an extended logic program we let:
is an extended logic program we let:

Example 64. We consider the extended logic program ![]() consisting of:
consisting of:

In the translated program ![]() , rules 1 and 2 are replaced by:
, rules 1 and 2 are replaced by:

We have two stable models of ![]() , as the reader can easily verify by inspecting Table 12.
, as the reader can easily verify by inspecting Table 12.

So, the answer sets of ![]() are
are ![]() and
and

We note that ![]() , but
, but ![]() and
and ![]() . This shows that negation-as-failure as interpreted in answer set programming does not realize a closed-world assumption in the strong sense that every atom
. This shows that negation-as-failure as interpreted in answer set programming does not realize a closed-world assumption in the strong sense that every atom ![]() that is not derivable is interpreted as strongly negated,
that is not derivable is interpreted as strongly negated, ![]() .Footnote 70
.Footnote 70
If we add the additional rule ![]() to
to ![]() , resulting in
, resulting in ![]() , we end up with one answer set, namely
, we end up with one answer set, namely

In terms of nonmonotonic consequence we have
 , while
, while  , and
, and , while
, while  and
and  .
.

Table 12Long description
The table consists of five columns: M subscript 1, M subscript 2, M subscript 3, M subscript 4, and M subscript 5. It read as follows: Row 1: working: checkmark, checkmark, checkmark, checkmark, checkmark. Row 2: Sunday Morning: checkmark, checkmark, checkmark, checkmark, checkmark. Row 3: jogging: checkmark, Blank, Blank, checkmark, checkmark. Row 4: jogging prime: Blank, checkmark, checkmark, Blank, checkmark. Row 5: stormy: Blank, Blank, checkmark, checkmark, checkmark. Row 6: r subscript 1 prime: checkmark, checkmark, checkmark, checkmark, checkmark. Row 7: r subscript 2 prime: checkmark, checkmark, checkmark, checkmark, checkmark.
Example 65. There are extended programs with only inconsistent (stable) models, for example, ![]() . The only model of
. The only model of ![]() is
is ![]() . So the only model of
. So the only model of ![]() is
is ![]() .
.
16.4 Answer Sets, Defaults, and Argumentation
Answer sets are closely related to the extensions of Reiter’s default logic (Section 12.2).Footnote 71 We can translate a clause of the form (16.3.1) to a (possibly) nonnormal default by

where for an atom ![]() ,
, ![]() and
and ![]() . Let the resulting translation of an extended program
. Let the resulting translation of an extended program ![]() be
be

Example 66. We have ![]() , where
, where ![]() consists of the following general default rules:
consists of the following general default rules:

Theorem 16.1 (Gelfond and Lifschitz, 1991). Let ![]() be an extended program and
be an extended program and ![]() . Then,
. Then,
1. if
 , then
, then  , and
, and2. for every
 there is exactly one
there is exactly one  for which
for which  .
.
Given this result the metatheoretic results for Reiter’s greedy approach immediately apply (see Section 12.1), such as cautious transitivity for ![]() .Footnote 72
.Footnote 72
In the following we show that answer sets can also be expressed in logical argumentation.Footnote 73 We will improve our previous naive attempt (see Section 16.1 and recall the problematic Example 58) by allowing for reinstatement.
Definition 16.5. Let ![]() be an extended logic program. We let
be an extended logic program. We let ![]() , where
, where ![]() and for
and for ![]() , we let
, we let ![]() attack
attack ![]() (in signs
(in signs ![]() ) if there is a sub-argument
) if there is a sub-argument ![]() of
of ![]() such that
such that ![]() .
.
Example 67 (Example 64 cont.). We consider ![]() and list arguments in
and list arguments in ![]() that give rise to the argumentation framework in Fig. 32 (left).
that give rise to the argumentation framework in Fig. 32 (left).

Table 011Long description
The list describes: 1. a subscript zero equals right arrow working; 2. a subscript one equals right arrow Sunday Morning; 3. b subscript one equals similarity jogging; 4. b subscript two equals similarity not jogging; 5. b subscript three equals similarity stormy; 6. c subscript one equals (a subscript one, b subscript two, b subscript three right arrow jogging); 7. c subscript two equals (a subscript zero, b subscript one right arrow not jogging).
We obtain two stable extensions of ![]() :
:

The set of conclusions (in ![]() ) of arguments in the two stable models correspond to the two answer sets of
) of arguments in the two stable models correspond to the two answer sets of ![]() , namely:
, namely:


Figure 32 Argumentation framework for Examples 67 (left) and 68 (right). We omit nonattacked arguments.
Example 68 (Example 58 cont.). We consider the problematic example for our naive argumentation-based account, ![]() . We have the following arguments in
. We have the following arguments in ![]() , giving rise to the argumentation framework in Fig. 32 (right).
, giving rise to the argumentation framework in Fig. 32 (right).
The unique stable extension of ![]() is
is ![]() (highlighted). The set of atoms in
(highlighted). The set of atoms in ![]() is identical to the only stable model of
is identical to the only stable model of ![]() , namely
, namely ![]() .
.

Table 012Long description
The table consists of three columns. It read as follows: Row 1: a subscript 1 not s; b subscript 1 equals right arrow s; b subscript 2 equals a subscript 1 right arrow q. Row 2: a subscript 2 equals not q; blank; b subscript 3 equals a subscript 2 right arrow r.
The correspondence is not coincidental. For a given extended logic program ![]() let
let ![]() be the set of consistent answer sets of
be the set of consistent answer sets of ![]() , that is, those stable models of
, that is, those stable models of ![]() that do not contain contradictory literals.Footnote 74
that do not contain contradictory literals.Footnote 74
Theorem⋆ 16.2. Let ![]() be an extended logic program.
be an extended logic program.
1. If
 , then
, then  .
.2. If
 and
and  , then
, then  .
.
Selected Further Readings
Friedman and Halpern (Reference Friedman and Halpern1996) provided a unifying approach to default reasoning based on plausibility orders covering many of the previously mentioned NMLs, such as the preferential semantics of Kraus et al. (Reference Kraus, Lehman and Magidor1990), the possibilistic approach by Benferhat et al. (Reference Benferhat, Dubois, Prade, Nebel, Rich and Swartout1992), ordinal rankings by Spohn (Reference Spohn, Harper and Skyrms1988), and ![]() -semantics (Adams, Reference Adams1975; Pearl, Reference Pearl1989). Another generalization is provided in Arieli and Avron (Reference Arieli and Avron200), who go beyond a classical base logic. Preferential conditionals have been embedded in the scope of a full logical language (so that they are allowed to occur in the scope of logical connectives such as
-semantics (Adams, Reference Adams1975; Pearl, Reference Pearl1989). Another generalization is provided in Arieli and Avron (Reference Arieli and Avron200), who go beyond a classical base logic. Preferential conditionals have been embedded in the scope of a full logical language (so that they are allowed to occur in the scope of logical connectives such as ![]() ) in conditional logics (Asher & Morreau, Reference Asher, Morreau and van Eijck1991; Boutilier, Reference Boutilier1994a; Friedman & Halpern, Reference Friedman and Halpern1996). First-order versions of preferential consequence relations and conditional logics have been investigated, for example, in Delgrande (Reference Delgrande1998; Friedman et al. (Reference Friedman, Halpern and Koller2000) and Lehmann and Magidor (Reference Lehmann and Magidor1990). Proof theories for conditional logics in the style of Kraus et al. (Reference Kraus, Lehman and Magidor1990) can be found in Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2009), and for rational closure in Straßer (Reference Straßer, Carnielli and D’Ottaviano2009b) in terms of adaptive logics. Deep connections between preferential approaches and belief revision have been observed in many places, for example, Boutilier (Reference Boutilier1994b), Gärdenfors (Reference Gärdenfors1990), Rott et al. (Reference Rott2021).
) in conditional logics (Asher & Morreau, Reference Asher, Morreau and van Eijck1991; Boutilier, Reference Boutilier1994a; Friedman & Halpern, Reference Friedman and Halpern1996). First-order versions of preferential consequence relations and conditional logics have been investigated, for example, in Delgrande (Reference Delgrande1998; Friedman et al. (Reference Friedman, Halpern and Koller2000) and Lehmann and Magidor (Reference Lehmann and Magidor1990). Proof theories for conditional logics in the style of Kraus et al. (Reference Kraus, Lehman and Magidor1990) can be found in Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2009), and for rational closure in Straßer (Reference Straßer, Carnielli and D’Ottaviano2009b) in terms of adaptive logics. Deep connections between preferential approaches and belief revision have been observed in many places, for example, Boutilier (Reference Boutilier1994b), Gärdenfors (Reference Gärdenfors1990), Rott et al. (Reference Rott2021).
Logics based on preferential semantics and logic programming have been characterized in terms of artificial neural nets; see for example Besold et al. (Reference Besold, d’Avila Garcez, Stenning, van der Torre and van Lambalgen2017), Hölldobler and Kalinke (Reference Hölldobler and Kalinke1994), and Leitgeb (Reference Leitgeb2018).
An overview and introduction to logic programming with an emphasis on answer sets is, in book form, Lifschitz (Reference Lifschitz2019), and more compactly, Eiter et al. (Reference Eiter, Ianni and Krennwallner2009). As the reader will expect, many variants of logic programming exist, including disjunctions (Minker, Reference Minker1994), preferences (Schaub & Wang, Reference Schaub and Wang2001), probabilities (Ng & Subrahmanian, Reference Ng and Subrahmanian1992) with connections to deep learning (Manhaeve et al., Reference Manhaeve, Dumanéiæ, Kimmig, Demeester and De Raedt2021), and so on. Logic programming has been successfully applied in the psychology of reasoning (Saldanha, Reference Saldanha2018; Stenning & Van Lambalgen, Reference Stenning and Van Lambalgen2008).
Acknowledgments
I want to thank Kees van Berkel, Matthis Hesse, Jessica Krumhus, and Dunja Šešelja for their highly valuable feedback on previous drafts. I am also much obliged to Joke Meheus and Diderik Batens for introducing me to the wonderful world of NMLs. Finally, not to forget Brad and Fred: thanks to my editors, Brad Armour-Garb and Fred Kroon, for their support, trust, and good mood throughout the whole process.
SUNY Albany
Bradley Armour-Garb is chair and Professor of Philosophy at SUNY Albany. His books include The Law of Non-Contradiction (co-edited with Graham Priest and J. C. Beall, 2004), Deflationary Truth and Deflationism and Paradox (both co-edited with J. C. Beall, 2005), Pretense and Pathology (with James Woodbridge, Cambridge University Press, 2015), Reflections on the Liar (2017), and Fictionalism in Philosophy (co-edited with Fred Kroon, 2020).
The University of Auckland
Frederick Kroon is Emeritus Professor of Philosophy at the University of Auckland. He has authored numerous papers in formal and philosophical logic, ethics, philosophy of language, and metaphysics, and is the author of A Critical Introduction to Fictionalism (with Stuart Brock and Jonathan McKeown-Green, 2018).
About the Series
This Cambridge Elements series provides an extensive overview of the many and varied connections between philosophy and logic. Distinguished authors provide an up-to-date summary of the results of current research in their fields and give their own take on what they believe are the most significant debates influencing research, drawing original conclusions.